GPT学习笔记-Embedding的降维与2D,3D可视化
嵌入(Embedding)在机器学习和自然语言处理中是一种表示离散变量(如单词、句子或整个文档)的方式,通常是作为高维向量或者矩阵。嵌入的目标是捕捉到输入数据中的语义信息,使得语义相近的元素在嵌入空间中的距离也比较近。
例如,在自然语言处理中,词嵌入是一种将单词或短语从词汇表映射到向量的技术。这些嵌入向量捕捉了词汇之间的语义和语法关系。例如,词嵌入可以捕捉到"king"和"queen","man"和"woman"之间的相似性,并且可以通过向量运算来表示语言的一些特性,如"king" - "man" + "woman" ≈ "queen"。
嵌入的维度是一个重要的参数,它决定了嵌入向量的大小。较小的维度可能无法捕捉到足够的语义信息,而较大的维度可能导致计算复杂性增加和过拟合的风险。嵌入的维度通常是一个需要调整的超参数,它的选择取决于多种因素,包括数据的复杂性(例如,词汇的大小和语言的复杂性)、模型的复杂性、计算资源的可用性,以及特定任务的需求。
在实际应用中,词嵌入的维度通常选取在几十到几百之间,例如,Word2Vec和GloVe等常用的词嵌入方法通常使用50, 100, 200或300维的嵌入。而在一些更复杂的模型(如BERT或GPT)中,嵌入的维度可能会达到几千。
在cookbook里面fine_food_reviews_with_embeddings_1k.csv这个数据集里面我们可以看到embedding如图所示
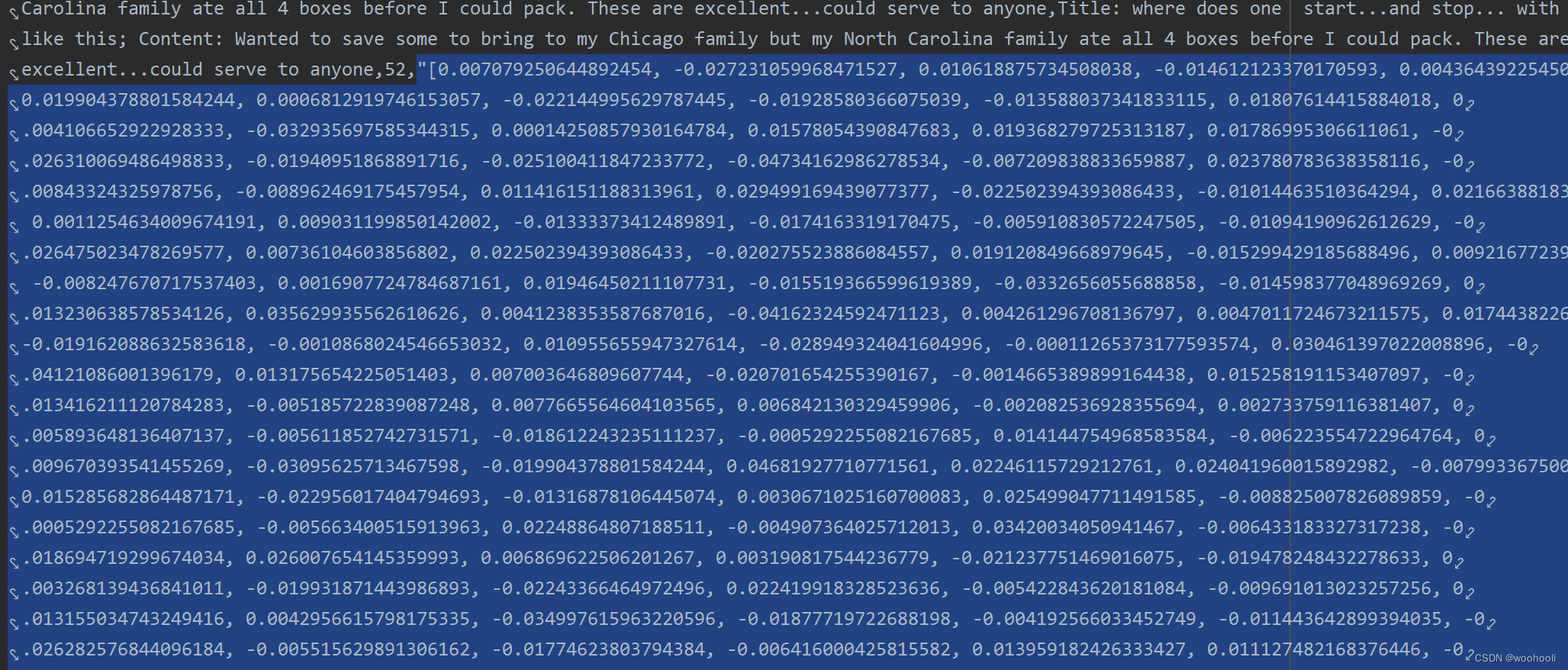
例子里的embedding维度大概是几百,没细数。
将高维嵌入(如文本嵌入)降维到2D(或3D)主要有两个原因:
-
可视化:人类更擅长理解二维或三维的数据,而高维数据往往难以直观理解。通过将高维嵌入降至2D或3D,我们可以直接在平面或空间中可视化数据,比如使用散点图来展示每个数据点。这使我们能够直观地观察数据点之间的相似性和差异性,从而更好地理解数据的分布和结构。
-
计算效率:高维数据通常需要更大的计算资源和存储空间。降维到2D或3D可以减少数据的复杂性,提高计算效率,同时也可以减少存储空间的需求。
值得注意的是,降维过程可能会损失一部分信息。因此,选择合适的降维方法(如PCA、t-SNE等)和降维后的维度是非常重要的,需要根据具体的应用需求和数据特性进行选择。
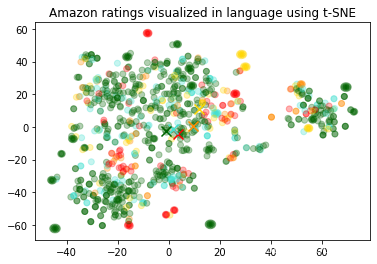
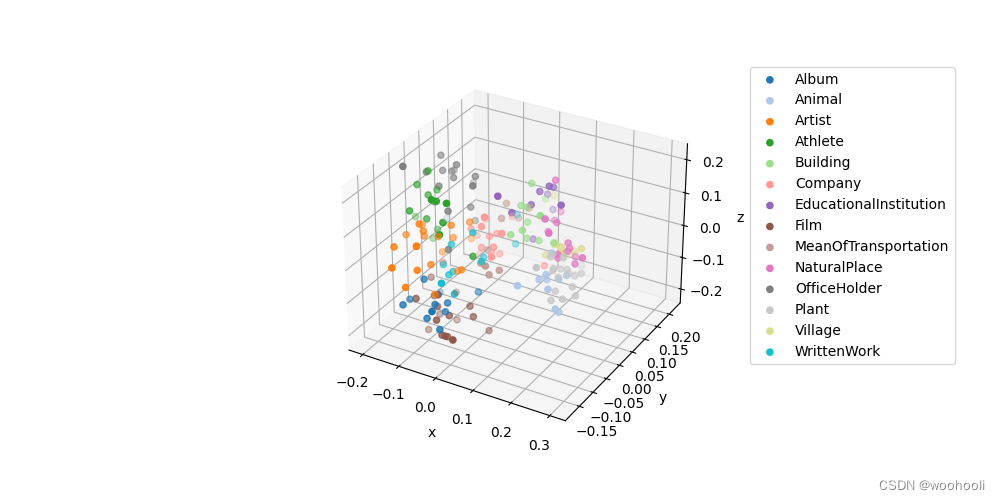
在例子里面有两个数据可视化的代码Visualizing_embeddings_in_3D,Visualizing_embeddings_in_2D,用的分别是PCA和t-SNE.
-
PCA(主成分分析):PCA是一种线性降维技术,它的目标是找到数据的主要特征方向(称为主成分),并用这些方向来表示数据。PCA通过对数据协方差矩阵进行特征分解,找到最大方差的方向作为第一主成分,然后在与之前的主成分正交的方向中找到最大方差的方向作为下一个主成分,以此类推。PCA的一个主要优点是它可以减少数据的噪声,并保留数据的主要特征。但是,PCA是一种线性技术,可能无法很好地处理非线性关系。
-
t-SNE(t-分布式随机邻域嵌入):t-SNE是一种非线性降维技术,特别适合于可视化高维数据集。t-SNE的目标是在低维空间中保持高维空间中的相似度关系。具体来说,t-SNE首先在高维空间中计算每对数据点的相似度,然后在低维空间中尽可能地保持这些相似度。t-SNE的一个主要优点是它可以很好地保持数据的局部结构,能够在低维空间中清晰地展示数据的聚类。但是,t-SNE的计算复杂性较高,可能不适合处理大规模数据集,而且t-SNE的结果可能受初始化和超参数的影响。
这两种方法都有各自的优点和局限性,选择哪种方法取决于具体的应用场景和需求。
例子代码执行后的结果。
相关文章:

GPT学习笔记-Embedding的降维与2D,3D可视化
嵌入(Embedding)在机器学习和自然语言处理中是一种表示离散变量(如单词、句子或整个文档)的方式,通常是作为高维向量或者矩阵。嵌入的目标是捕捉到输入数据中的语义信息,使得语义相近的元素在嵌入空间中的距…...

Nautilus Chain上线主网,为DeFi和流支付的未来构建基础
近日,加密行业权威平台 Coinmarketcap 发表了一篇名为“Zebec 模块化 Layer3 链 Nautilus Chain上线主网,为 DeFi 和流支付的未来构建基础”的文章,文中对 Zebec 生态公链 Nautilus Chain 的生态进展进行了简要的报道,并对其进行了…...

java设计模式之命令设计模式的前世今生
命令设计模式是什么? 命令设计模式是一种行为型设计模式,它允许将请求封装为对象,并将其传递给调用者,从而使调用者可以在不知道请求具体细节的情况下进行操作。命令模式的主要目的是解耦请求的发送者和接收者,以及通…...
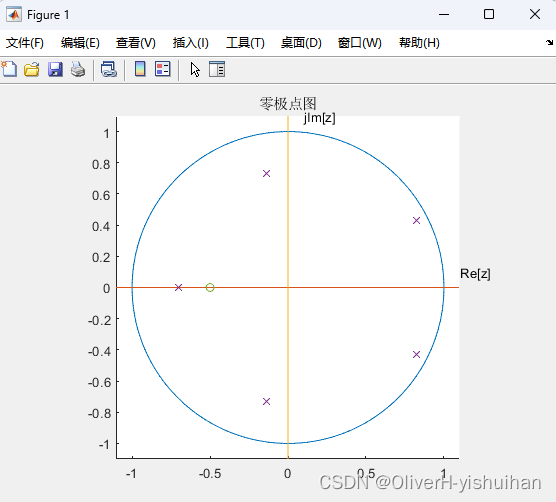
离散系统函数零积点分析
离散系统函数零积点分析 在 Matlab中,系统函数的零极点就可以通过函数 roots 得到。 函数的零极点也可以通过函数 tf2zp 获得,其调用格式为:[Z, P, K] tf2zp(B, A),函数 tf2zp 可以将H(z)的有理分式转换为零极点增益形式&#…...

Karl Guttag:苹果VST MR头显也无法突破AR的物理局限
据近期的爆料、传闻显示,苹果将6月份的WWDC2023上首次公布AR/VR头显。对此,AR/VR光学专家Karl Guttag持怀疑态度,他此前在DisplayDaily的文章中写道,苹果研发AR/VR头显更像是担心错过新技术趋势。回顾过去的一些关键的AR产品&…...
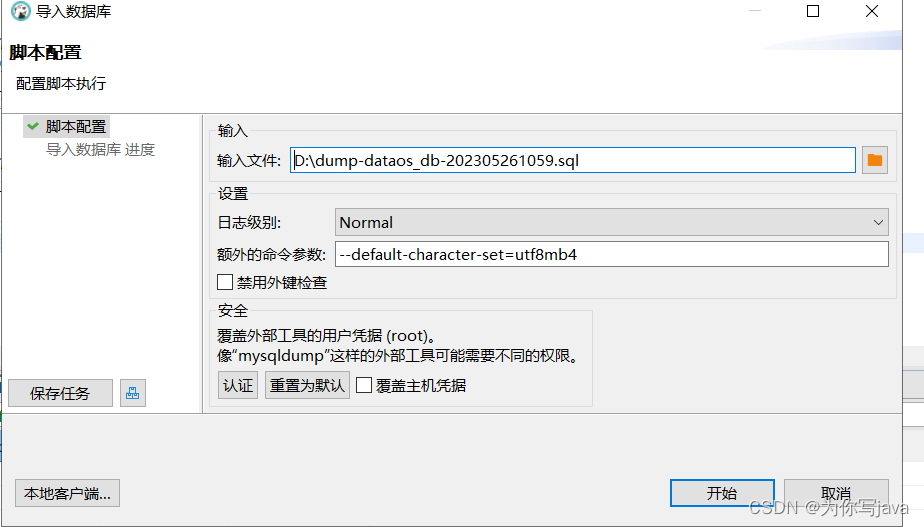
mysql倒库操作遇到的问题
背景:本地windows 10安装了mysql数据库后,需要把远程库的表结构和数据全部导入进来。 操作:导出数据库,导入数据库。 第一步:导出数据库 使用dump命令即可。 登陆mysql数据库 mysql -hhost --default-character-s…...
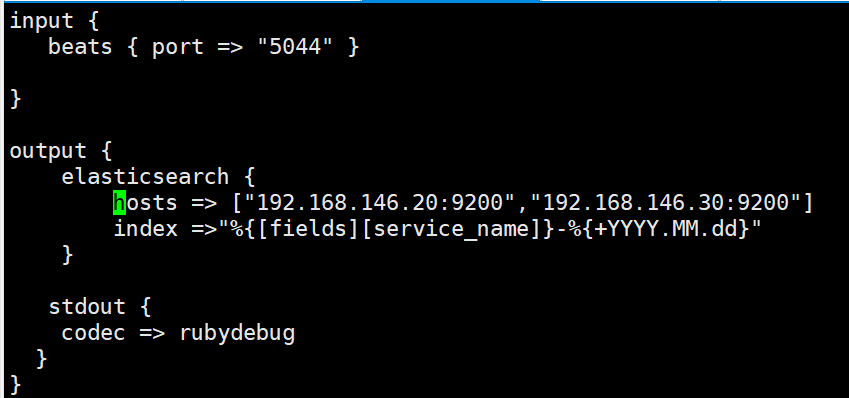
ELK企业级日志分析系统
ELK概述 为什么要使用 ELK 日志主要包括系统日志、应用程序日志和安全日志。系统运维和开发人员可以通过日志了解服务器软硬件信息、检查配置过程中的错误及错误发生的原因。经常分析日志可以了解服务器的负荷,性能安全性,从而及时采取措施纠正错误。 …...

华为OD机试真题 Java 实现【基站维修工程师】【2023Q1 200分】,附详细解题思路
一、题目描述 小王是一名基站维护工程师,负责某区域的基站维护。 某地方有n个基站(1<n<10),已知各基站之间的距离s(0<s<500),并且基站x到基站y的距离,与基站y到基站x的距离并不一定会相同。 小王从基站1出发,途径每个基站1次,然后返回基站1,需要请你…...

SSM 如何使用 TCC 机制实现分布式事务?
SSM 如何使用 TCC 机制实现分布式事务? 分布式事务是现代分布式系统中必不可少的一部分,而 TCC 机制(Try-Confirm-Cancel)是一种常用的分布式事务处理方式。在 SSM 框架中,我们可以使用 TCC 机制来管理分布式事务。本…...
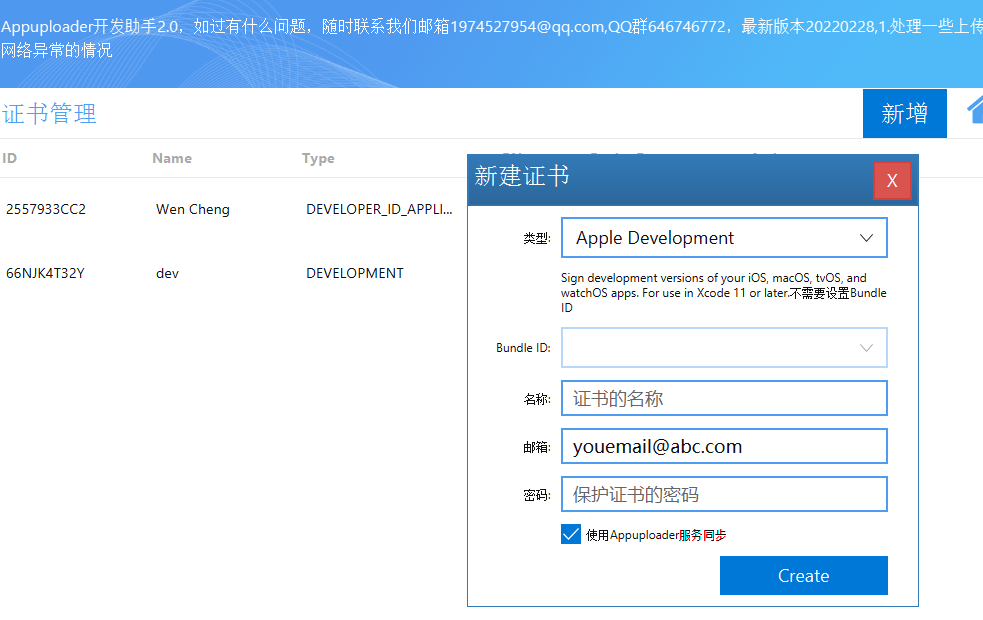
如何在上架App之前设置证书并上传应用
App上架教程 在上架App之前想要进行真机测试的同学,请查看《iOS- 最全的真机测试教程》,里面包含如何让多台电脑同时上架App和真机调试。 P12文件的使用详解 注意: 同样可以在Build Setting 的sign中设置证书,但是有点麻烦&…...

华清远见 day04
break 打破循环,再也不执行 continue 跳出本次循环,继续执行下一次循环; 常量 字面常量 宏常量 #define A 100 //定义一个宏常量, 名为:A 值为:100 位置 在 头文件 下面 ,文件开头 输入时间秒 得到 小时 分钟 秒的时间输出 用到 三运算符; 宏常量 Mi 是60 t1 /Mi>6…...

如何处理Vue应用程序中的错误和异常情况?
处理Vue应用程序中的错误和异常情况是开发中非常重要的一环,但是对于新手来说,这往往是一个比较棘手的问题。不过别担心,下面我将为大家详细解答。 首先,我们需要知道的是,在Vue中,错误和异常情况是两个不…...

javascript基础十六:Ajax 原理是什么?如何实现?
一、是什么 AJAX全称(Async Javascript and XML) 即异步的JavaScript 和XML,是一种创建交互式网页应用的网页开发技术,可以在不重新加载整个网页的情况下,与服务器交换数据,并且更新部分网页 Ajax的原理简单来说通过XmlHttpRequ…...

大话手游原始服务端搭建教程Centos
大话手游原始服务端搭建教程Centos 大家好,我是艾西,今天给大家分享一款回合制的ARPG大话手游搭建教程。游戏场景、精美的画面以及多元的人物做的非常棒。在游戏中可以穿越神话世界,同时也可以结交好友,加入团队,共同…...

C语言中的通用工具库stdlib.h
目录 1、malloc和free:用于动态内存分配和释放。 2、atoi和atof:用于将字符串转换为整数或浮点数。 3、rand和srand:用于生成随机数和设置随机数种子。 4、system:用于执行系统命令。 5、exit:用于退出程序。 6、…...
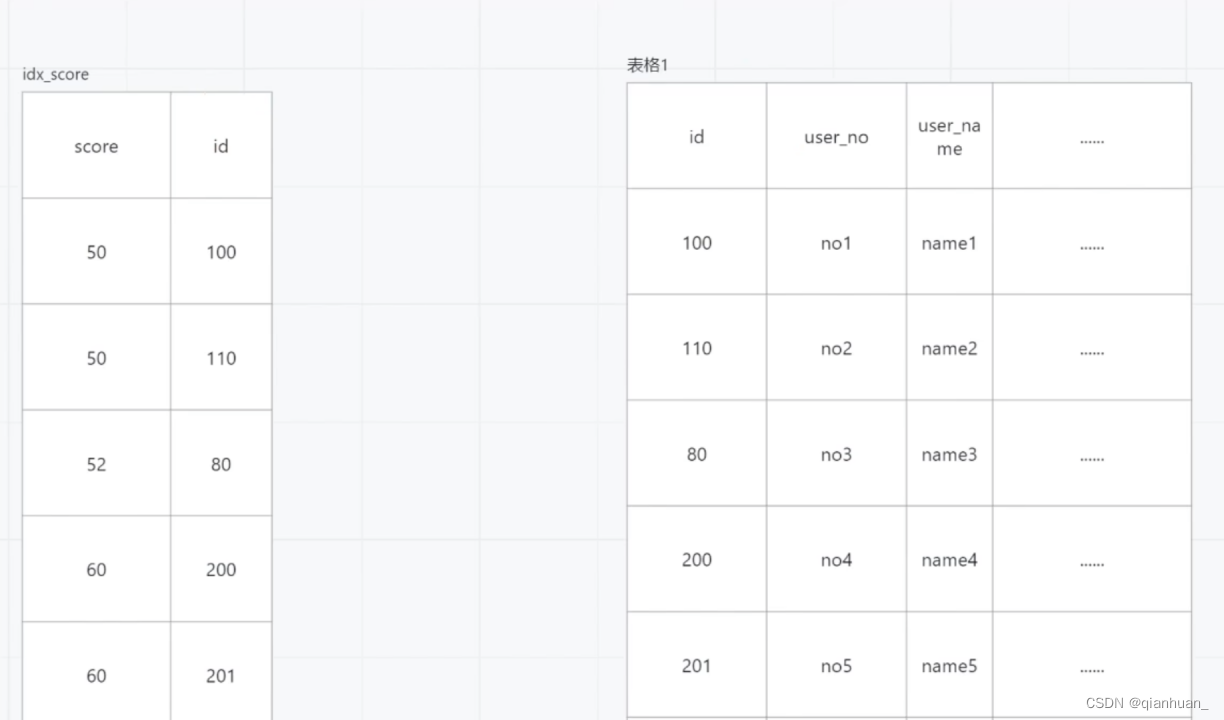
优化带排序的分页查询
优化带排序的分页查询 浅分页: select user_no,user_name,socre from student order by score desc limit 5,20 深分页: select user_no,user_name,socre from student order by score desc limit 80000,20 因为偏移量深分页更大,所以深分页执…...

chatgpt赋能python:Python如何删除空白
Python 如何删除空白 在SEO优化过程中,我们需要保证我们的网页内容的质量和可读性。其中,一个重要的因素是删除空白。在Python中,我们可以使用多种方法来删除空白,下面我们将介绍一些方法并讨论它们的优缺点。 方法一࿱…...

[论文阅读] Explicit Visual Prompting for Low-Level Structure Segmentations
[论文地址] [代码] [CVPR 23] Abstract 我们考虑了检测图像中低层次结构的通用问题,其中包括分割被操纵的部分,识别失焦像素,分离阴影区域,以及检测隐藏的物体。每个问题通常都有一个特定领域的解决方案,我们表明&am…...
swagger在spring项目中的使用
一、Swagger2介绍 前后端分离开发模式中,api文档是最好的沟通方式。 Swagger 是一个规范和完整的框架,用于生成、描述、调用和可视化 RESTful 风格的 Web 服务。 及时性 (接口变更后,能够及时准确地通知相关前后端开发人员)规范性 (并且保…...
操作系统第五章——输入输出管理(中)
提示:若我会见到你,事隔经年,我如何向你招呼,以眼泪,以沉默 文章目录 5.2.1 IO核心子系统知识总览功能要在那个层次实现 5.2.2 假脱机技术(SPOOLing)知识总览什么是脱机技术假脱机技术——输入井…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
