离散系统函数零积点分析
离散系统函数零积点分析
在 Matlab中,系统函数的零极点就可以通过函数 roots 得到。
函数的零极点也可以通过函数 tf2zp 获得,其调用格式为:[Z, P, K] = tf2zp(B, A),函数 tf2zp 可以将H(z)的有理分式转换为零极点增益形式,B、A分别表示 H(z) 的分子、分母多项式的系统向量,
- Z 表示零点向量,P 表示极点向量,K 表示系统增益。
函数 zplane 用于绘制 H(z)的零极点图,其调用形式为:zplane(z, p),绘制出列向量 z 中的零点(以符号 o 表示)和 p 中的极点(以符号 x 表示)。
说明:如果 z 和 p 为矩阵,则会以不同的颜色绘制出 z 和 p 各列中的零点和极点。
% E_6_5.m
% 已知某离散系统的系统函数如下。试用 Matlab 求出该系统的零极点,并画出零极点分布图,判断系统是否稳定。
% 系统函数为:H(z) = (2*z + 1)/(3*z^5 - 2*z^4 + 1)
% E_6_5.m
% 已知某离散系统的系统函数如下。试用 Matlab 求出该系统的零极点,
% 并画出零极点分布图,判断系统是否稳定。
% 系统函数为:H(z) = (2*z + 1)/(3*z^5 - 2*z^4 + 1)% 绘制零极点分布图的实现程序
a = [3 -2 0 0 0 1];
b = [2 1];
% ljdt(a,b);
% % % % % % 函数ljdt % % START % % % % % % % % % % % % % % % %
% function ljdt(A,B)
p = roots(a); % 求系统极点
q = roots(b); % 求系统零点
p = p'; % 将极点列向量转置为行向量
q = q'; % 将零点列向量转置为行向量
x = max(abs([p q 1])); % 确定纵坐标范围
x = x + 0.1;
y = x;
hold on
axis([-x x -y y]);
w = 0:pi/300:2*pi;
t = exp(1i*w);
plot(t); % 画出单位圆
axis('square');
plot([-x x], [0 0]);
plot([0 0], [-y y]);
text(0.1, x, 'jIm[z]');
text(y, 1/10, 'Re[z]');
plot(real(p), imag(p), 'x');
plot(real(q), imag(q), 'o');
title('零极点图');
hold off;
% end
% % % % % % % % 函数ljdt % % END % % % % % % % % % % % % % % % %
p = roots(a)
q = roots(b)
pa = abs(p)% 该系统的所有极点都位于 Z 平面的单位圆内,故该系统为稳定系统。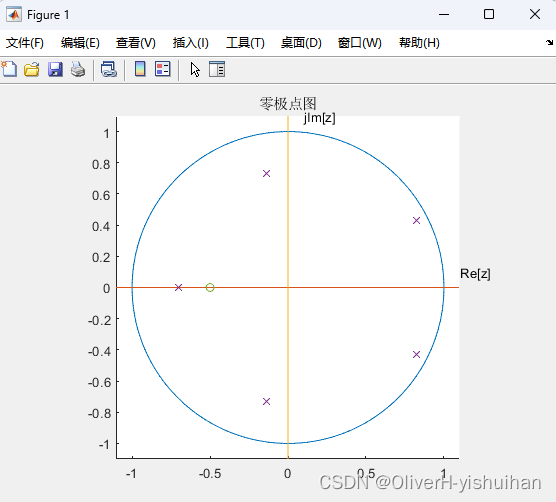
该系统的所有极点都位于 Z 平面的单位圆内,故该系统为稳定系统。
相关文章:

离散系统函数零积点分析
离散系统函数零积点分析 在 Matlab中,系统函数的零极点就可以通过函数 roots 得到。 函数的零极点也可以通过函数 tf2zp 获得,其调用格式为:[Z, P, K] tf2zp(B, A),函数 tf2zp 可以将H(z)的有理分式转换为零极点增益形式&#…...

Karl Guttag:苹果VST MR头显也无法突破AR的物理局限
据近期的爆料、传闻显示,苹果将6月份的WWDC2023上首次公布AR/VR头显。对此,AR/VR光学专家Karl Guttag持怀疑态度,他此前在DisplayDaily的文章中写道,苹果研发AR/VR头显更像是担心错过新技术趋势。回顾过去的一些关键的AR产品&…...
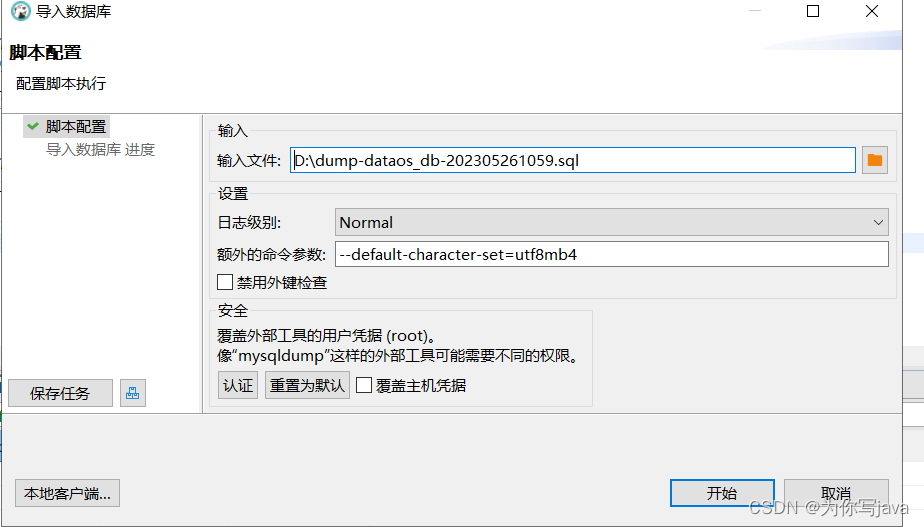
mysql倒库操作遇到的问题
背景:本地windows 10安装了mysql数据库后,需要把远程库的表结构和数据全部导入进来。 操作:导出数据库,导入数据库。 第一步:导出数据库 使用dump命令即可。 登陆mysql数据库 mysql -hhost --default-character-s…...
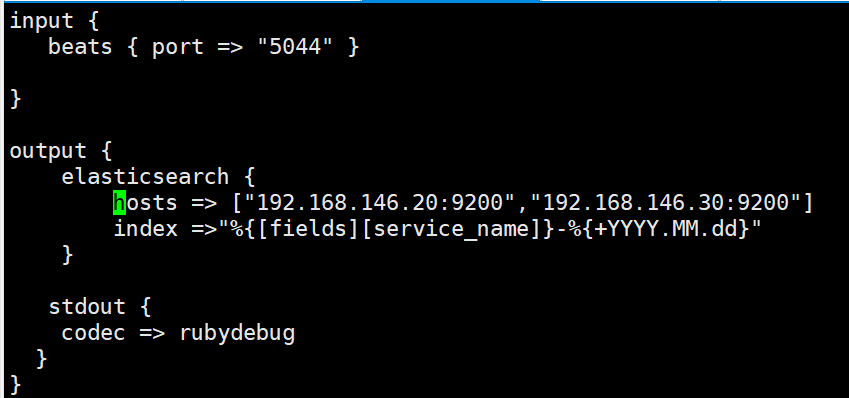
ELK企业级日志分析系统
ELK概述 为什么要使用 ELK 日志主要包括系统日志、应用程序日志和安全日志。系统运维和开发人员可以通过日志了解服务器软硬件信息、检查配置过程中的错误及错误发生的原因。经常分析日志可以了解服务器的负荷,性能安全性,从而及时采取措施纠正错误。 …...

华为OD机试真题 Java 实现【基站维修工程师】【2023Q1 200分】,附详细解题思路
一、题目描述 小王是一名基站维护工程师,负责某区域的基站维护。 某地方有n个基站(1<n<10),已知各基站之间的距离s(0<s<500),并且基站x到基站y的距离,与基站y到基站x的距离并不一定会相同。 小王从基站1出发,途径每个基站1次,然后返回基站1,需要请你…...

SSM 如何使用 TCC 机制实现分布式事务?
SSM 如何使用 TCC 机制实现分布式事务? 分布式事务是现代分布式系统中必不可少的一部分,而 TCC 机制(Try-Confirm-Cancel)是一种常用的分布式事务处理方式。在 SSM 框架中,我们可以使用 TCC 机制来管理分布式事务。本…...
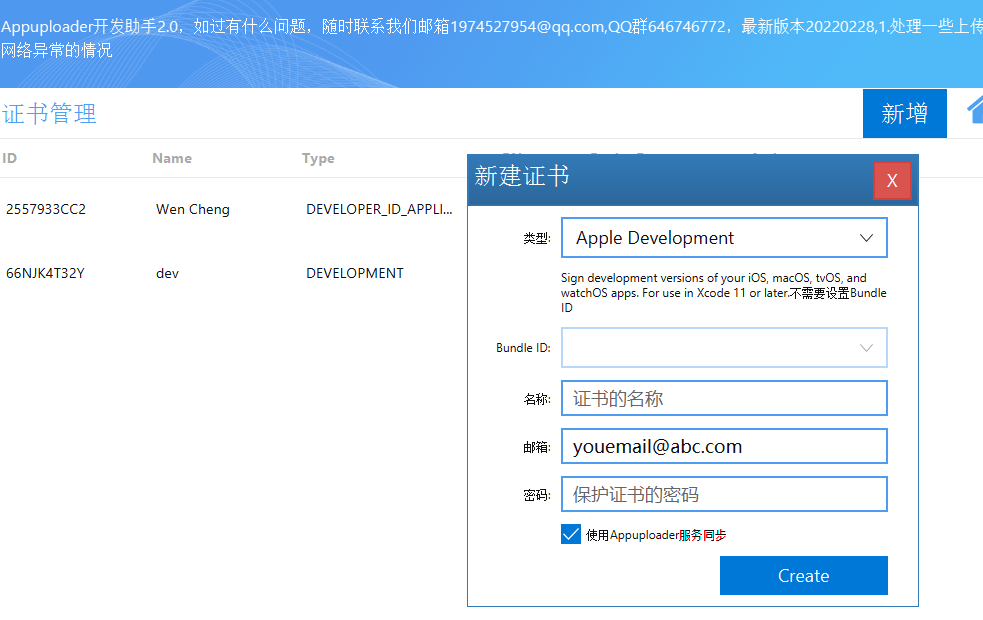
如何在上架App之前设置证书并上传应用
App上架教程 在上架App之前想要进行真机测试的同学,请查看《iOS- 最全的真机测试教程》,里面包含如何让多台电脑同时上架App和真机调试。 P12文件的使用详解 注意: 同样可以在Build Setting 的sign中设置证书,但是有点麻烦&…...

华清远见 day04
break 打破循环,再也不执行 continue 跳出本次循环,继续执行下一次循环; 常量 字面常量 宏常量 #define A 100 //定义一个宏常量, 名为:A 值为:100 位置 在 头文件 下面 ,文件开头 输入时间秒 得到 小时 分钟 秒的时间输出 用到 三运算符; 宏常量 Mi 是60 t1 /Mi>6…...

如何处理Vue应用程序中的错误和异常情况?
处理Vue应用程序中的错误和异常情况是开发中非常重要的一环,但是对于新手来说,这往往是一个比较棘手的问题。不过别担心,下面我将为大家详细解答。 首先,我们需要知道的是,在Vue中,错误和异常情况是两个不…...

javascript基础十六:Ajax 原理是什么?如何实现?
一、是什么 AJAX全称(Async Javascript and XML) 即异步的JavaScript 和XML,是一种创建交互式网页应用的网页开发技术,可以在不重新加载整个网页的情况下,与服务器交换数据,并且更新部分网页 Ajax的原理简单来说通过XmlHttpRequ…...

大话手游原始服务端搭建教程Centos
大话手游原始服务端搭建教程Centos 大家好,我是艾西,今天给大家分享一款回合制的ARPG大话手游搭建教程。游戏场景、精美的画面以及多元的人物做的非常棒。在游戏中可以穿越神话世界,同时也可以结交好友,加入团队,共同…...

C语言中的通用工具库stdlib.h
目录 1、malloc和free:用于动态内存分配和释放。 2、atoi和atof:用于将字符串转换为整数或浮点数。 3、rand和srand:用于生成随机数和设置随机数种子。 4、system:用于执行系统命令。 5、exit:用于退出程序。 6、…...
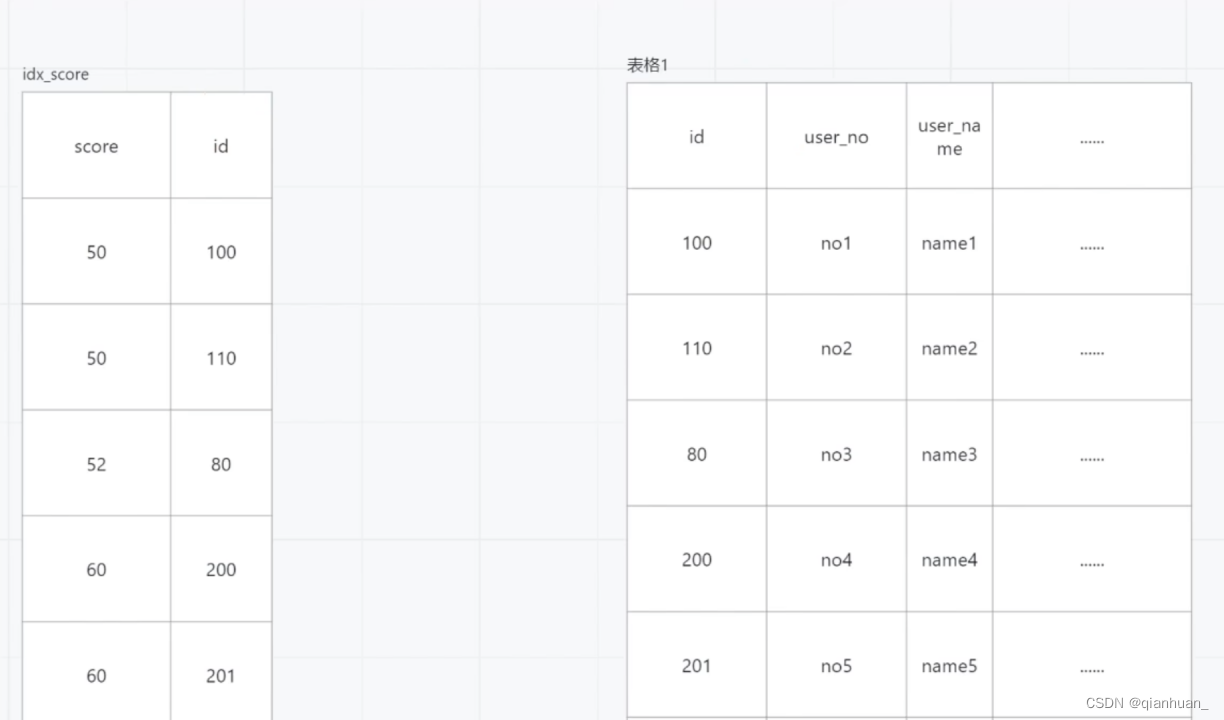
优化带排序的分页查询
优化带排序的分页查询 浅分页: select user_no,user_name,socre from student order by score desc limit 5,20 深分页: select user_no,user_name,socre from student order by score desc limit 80000,20 因为偏移量深分页更大,所以深分页执…...

chatgpt赋能python:Python如何删除空白
Python 如何删除空白 在SEO优化过程中,我们需要保证我们的网页内容的质量和可读性。其中,一个重要的因素是删除空白。在Python中,我们可以使用多种方法来删除空白,下面我们将介绍一些方法并讨论它们的优缺点。 方法一࿱…...

[论文阅读] Explicit Visual Prompting for Low-Level Structure Segmentations
[论文地址] [代码] [CVPR 23] Abstract 我们考虑了检测图像中低层次结构的通用问题,其中包括分割被操纵的部分,识别失焦像素,分离阴影区域,以及检测隐藏的物体。每个问题通常都有一个特定领域的解决方案,我们表明&am…...
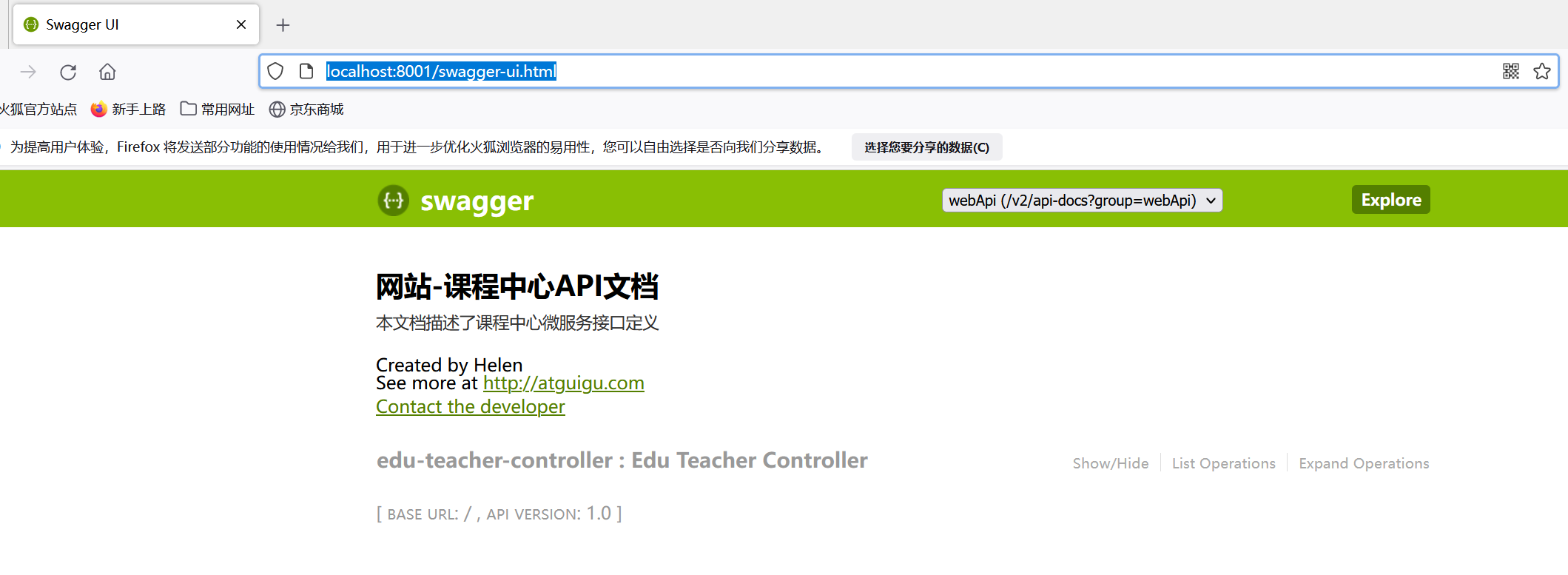
swagger在spring项目中的使用
一、Swagger2介绍 前后端分离开发模式中,api文档是最好的沟通方式。 Swagger 是一个规范和完整的框架,用于生成、描述、调用和可视化 RESTful 风格的 Web 服务。 及时性 (接口变更后,能够及时准确地通知相关前后端开发人员)规范性 (并且保…...
操作系统第五章——输入输出管理(中)
提示:若我会见到你,事隔经年,我如何向你招呼,以眼泪,以沉默 文章目录 5.2.1 IO核心子系统知识总览功能要在那个层次实现 5.2.2 假脱机技术(SPOOLing)知识总览什么是脱机技术假脱机技术——输入井…...
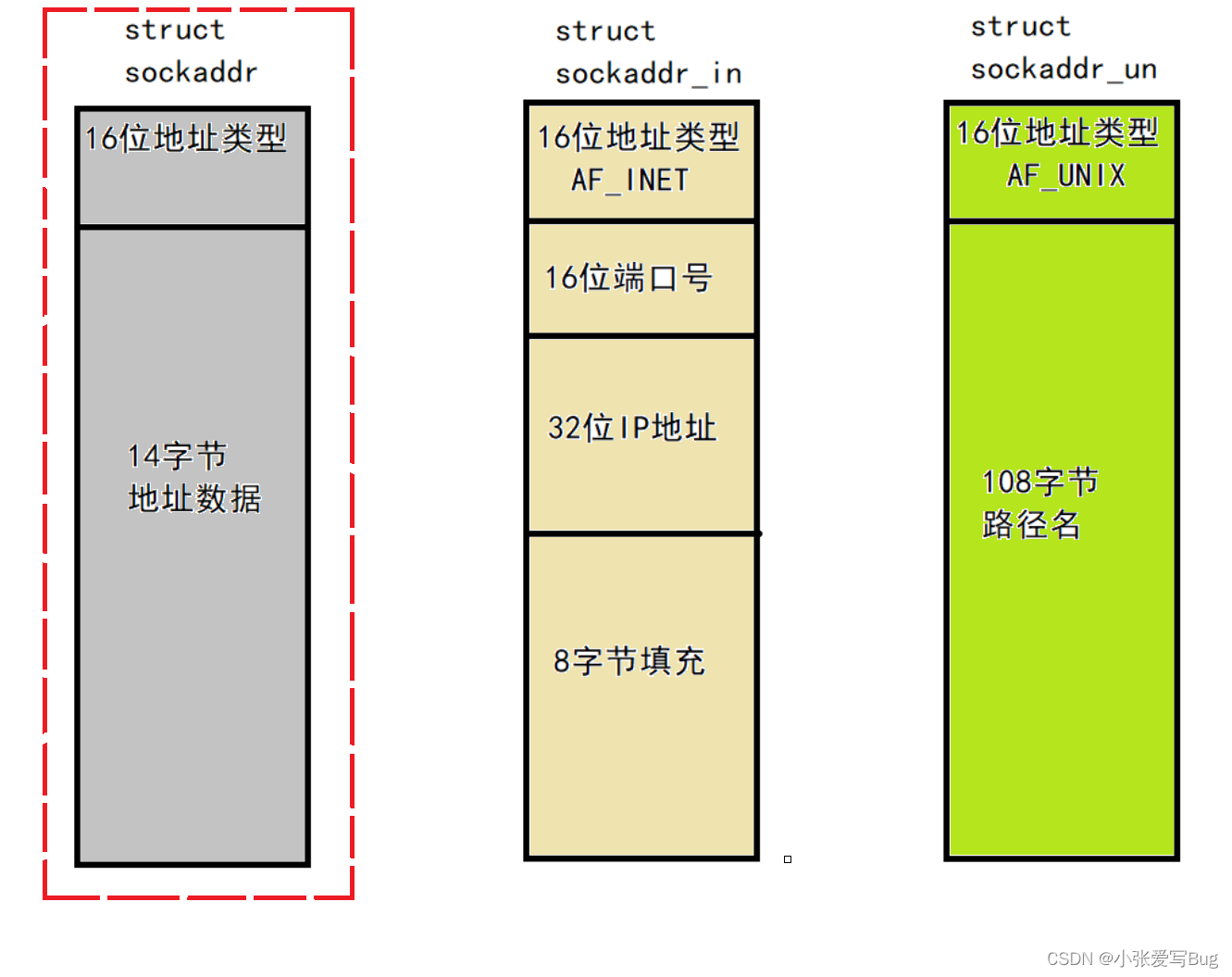
【网络】socket套接字基础知识
目录 IP地址和端口号 源IP地址和目的IP地址 端口号 源端口号和目的端口号 TCP/UDP协议 网络字节序 大小端 如何定义网络数据流地址 网络字节序和主机字节序的转换 socket编程接口 sockaddr结构 IP地址和端口号 源IP地址和目的IP地址 在IP数据包头部中,会…...

Go语言介绍以及Go语言环境安装
初步介绍: Go 是一个开源的编程语言,它能让构造简单、可靠且高效的软件变得容易。 Go是从2007年末由Robert Griesemer, Rob Pike, Ken Thompson主持开发,后来还加入了Ian Lance Taylor, Russ Cox等人,并最终于2009年11月开源&am…...

FPGA纯verilog实现CameraLink视频接收和发送,附带工程源码和技术支持
目录 1、前言2、CameraLink协议基础3、目前我已有的CameraLink收发工程4、设计方案5、CameraLink解码模块详解6、CameraLink编码模块详解7、vivado工程详解8、上板调试验证9、福利:工程代码的获取 1、前言 FPGA实现CameraLink视频编解码目前有两种方案:…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
