《算法导论》拓展之 一维二维最近点对问题
一维点对问题
描述:一维最近点对问题是指在给定的一维点集中找到距离最近的两个点。具体来说,给定一维坐标轴上的 n 个点,要找出其中的两个点,使它们的距离最小。
解决办法:解决这个问题的一种常见方法是使用排序和线性扫描。下面是这种算法的一般步骤:
- 排序:将点集按照坐标从小到大进行排序。
- 初始化最小距离:设定初始最小距离为正无穷大。
- 线性扫描:从左到右遍历排序后的点集。对于每个点,计算它与其右边相邻点的距离,并更新最小距离。
- 返回最小距离。
通过对点集进行排序,可以保证相邻的点在坐标上是接近的,因此只需要线性扫描一次即可找到最小距离的点对。该算法的时间复杂度为 O(n log n),其中 n 是点集中点的数量。
需要注意的是,在实际实现中,可以使用欧几里得距离公式计算点对之间的距离,并且在处理边界情况时要注意边界的处理和优化,以提高算法的效率。
总结来说,一维最近点对问题通过排序和线性扫描的方法解决。该算法利用了排序后点在坐标上的接近性,通过线性扫描找到最小距离的点对。
代码实现:
下面的这段代码实现了一个找出排序后数组中相邻元素差值最小的算法。其主要思路如下: - 首先定义了一个全局常量 N,用于表示输入数组的最大长度。同时定义了一个数组 A,用于保存输入的数组。
- 实现了一个名为 closet_pot 的递归函数,用于在指定区间内查找相邻元素差值的最小值.
首先,判断区间的大小。如果区间只有一个元素,返回正无穷表示不存在相邻元素。- 如果区间只有两个元素,直接返回这两个元素的差值。
- 否则,将区间分为两个子区间,分别递归调用 closet_pot 函数。
- 得到左子区间的最小差值 a,右子区间的最小差值 b。
- 然后取 a 和 b 中的较小值作为当前区间的最小差值 Min。
- 还需要比较当前区间中相邻两个元素的差值,即 A[mid+1] - A[mid],将其与 Min 比较,更新 Min。
- 最后,返回 Min 作为当前区间的最小差值。
- 在 main 函数中,首先读取输入的数组大小 n。
- 然后,通过循环读取 n 个整数,将它们保存到数组 A 中。
- 接下来,对数组 A 进行排序,以便找出相邻元素差值的最小值。
- 调用 closet_pot 函数,并传入数组的起始下标 0 和结束下标 n-1。
- 输出最小差值结果。
- 最后,使用 system(“pause”) 命令使程序暂停,防止控制台窗口关闭。
总结来说,这段代码通过递归的方式,在排序后的数组中查找相邻元素差值的最小值。通过不断地将区间划分为更小的子区间,并比较子区间的最小差值,最终找到整个数组中相邻元素差值的最小值。
#include <iostream>
#include <algorithm>
#include <climits>
#include <vector>
using namespace std;int closet_pot(vector<int>& A, int p, int q)
{if (p == q)return INT_MAX;if (p == q - 1)return A[q] - A[p];int mid = (p + q) / 2;int a = closet_pot(A, p, mid);int b = closet_pot(A, mid + 1, q);int Min = min(a, b);Min = min(Min, A[mid + 1] - A[mid]);return Min;
}int main()
{int n;cin >> n;vector<int> A(n);for (int i = 0; i < n; i++)cin >> A[i];sort(A.begin(), A.end());cout << closet_pot(A, 0, n - 1) << endl;return 0;
}
二维点对问题
描述:二维平面上的最近点对问题是指在给定的点集中找到距离最近的两个点对。具体来说,给定平面上的 n 个点,要找出其中的两个点,使它们的距离最小。
解决办法:解决这个问题的一种常见方法是使用分治算法。下面是这种算法的一般步骤:
- 排序:按照点的 x 坐标进行排序,从左到右对点集进行排序。
- 基本情况处理:如果点集中只有两个或三个点,可以直接计算它们之间的距离,并找到最小距离的点对。
- 分割:将点集平均地分成两个子集,左边和右边。取中间点将平面分成两个部分。
- 递归求解:对左右两个子集递归地应用最近点对算法,得到左边和右边的最近点对。
- 合并:计算左右两个子集的最近点对的距离。然后,从两个子集中选择距离更小的点对作为当前最近点对。
- 跨越边界:接下来需要考虑跨越两个子集边界的最近点对。为了找到这些点对,以中间点为界限,向左右两侧延伸一个距离为当前最小距离的区域。
- 在跨越边界区域内,使用简单的扫描方法,计算可能的最近点对。由于该区域内的点的数量是有限的,因此复杂度仍然是线性的。
- 最后,从左右两个子集的最近点对和跨越边界区域的最近点对中选择距离最小的点对作为最终的最近点对。
通过分治策略,最近点对问题的时间复杂度可以控制在 O(n log n) 的级别。
注意:在实际实现中,可以使用欧几里得距离公式计算点对之间的距离,并且在处理边界情况时要注意边界的处理和优化,以提高算法的效率。
总结:二维平面上的最近点对问题通过将点集进行排序、分割、递归求解、合并和跨越边界的步骤来解决。该算法利用了分治的思想,通过逐步缩小问题规模并处理边界情况,找到平面上距离最近的两个点对。
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
#include <limits>using namespace std;struct Point {double x;double y;
};bool compareX(const Point& p1, const Point& p2) {return p1.x < p2.x;
}bool compareY(const Point& p1, const Point& p2) {return p1.y < p2.y;
}double euclideanDistance(const Point& p1, const Point& p2) {double dx = p2.x - p1.x;double dy = p2.y - p1.y;return sqrt(dx * dx + dy * dy);
}double bruteForce(const vector<Point>& points, int start, int end) {double minDist = numeric_limits<double>::max();for (int i = start; i <= end; ++i) {for (int j = i + 1; j <= end; ++j) {double dist = euclideanDistance(points[i], points[j]);minDist = min(minDist, dist);}}return minDist;
}double closestPairUtil(const vector<Point>& points, int start, int end) {if (end - start <= 2) {return bruteForce(points, start, end);}int mid = (start + end) / 2;double midX = points[mid].x;double dl = closestPairUtil(points, start, mid);double dr = closestPairUtil(points, mid + 1, end);double d = min(dl, dr);vector<Point> strip;for (int i = start; i <= end; ++i) {if (abs(points[i].x - midX) < d) {strip.push_back(points[i]);}}sort(strip.begin(), strip.end(), compareY);double stripMin = d;int stripSize = strip.size();for (int i = 0; i < stripSize; ++i) {for (int j = i + 1; j < stripSize && (strip[j].y - strip[i].y) < stripMin; ++j) {double dist = euclideanDistance(strip[i], strip[j]);stripMin = min(stripMin, dist);}}return min(d, stripMin);
}double closestPair(const vector<Point>& points) {int n = points.size();vector<Point> sortedPoints = points;sort(sortedPoints.begin(), sortedPoints.end(), compareX);return closestPairUtil(sortedPoints, 0, n - 1);
}int main() {vector<Point> points = { {2, 3}, {12, 30}, {40, 50}, {5, 1}, {12, 10}, {3, 4} };double minDist = closestPair(points);cout << "最近点对的距离: " << minDist << endl;return 0;
}
相关文章:

《算法导论》拓展之 一维二维最近点对问题
一维点对问题 描述:一维最近点对问题是指在给定的一维点集中找到距离最近的两个点。具体来说,给定一维坐标轴上的 n 个点,要找出其中的两个点,使它们的距离最小。 解决办法:解决这个问题的一种常见方法是使用排序和线…...

【C++】动态存储分配
动态存储分配是指在程序运行时根据需要动态地分配和释放内存空间。 C中提供了两个关键的运算符用于动态存储分配:new和delete。 使用new运算符可以在堆(heap)上动态地分配内存空间,并返回所分配内存的首地址。语法如下࿱…...
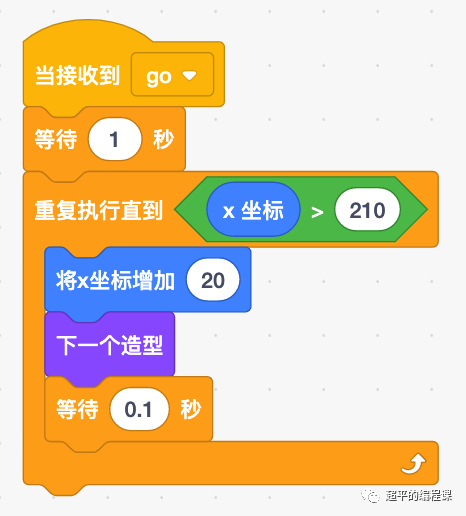
小狗避障-第14届蓝桥杯省赛Scratch中级组真题第4题
[导读]:超平老师的《Scratch蓝桥杯真题解析100讲》已经全部完成,后续会不定期解读蓝桥杯真题,这是Scratch蓝桥杯真题解析第139讲。 小狗避障,本题是2023年5月7日举行的第14届蓝桥杯省赛Scratch图形化编程中级组编程第4题…...
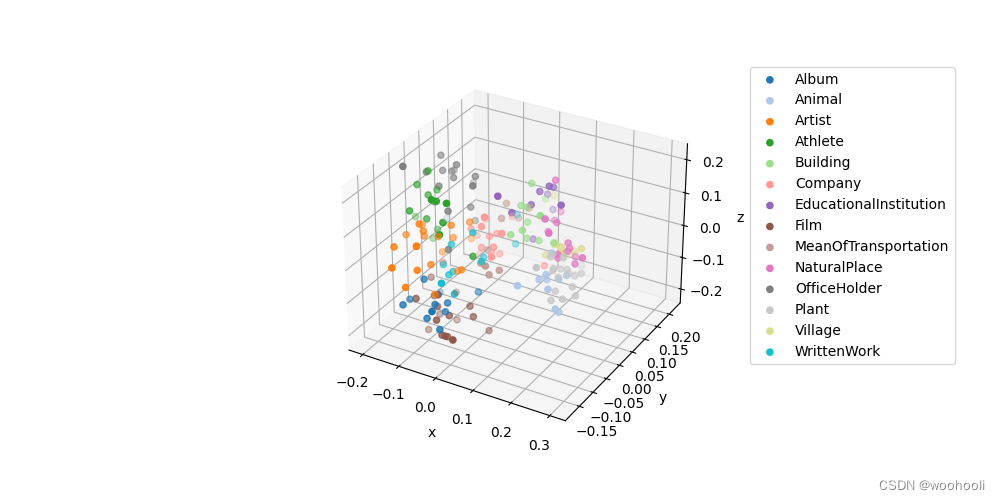
GPT学习笔记-Embedding的降维与2D,3D可视化
嵌入(Embedding)在机器学习和自然语言处理中是一种表示离散变量(如单词、句子或整个文档)的方式,通常是作为高维向量或者矩阵。嵌入的目标是捕捉到输入数据中的语义信息,使得语义相近的元素在嵌入空间中的距…...

Nautilus Chain上线主网,为DeFi和流支付的未来构建基础
近日,加密行业权威平台 Coinmarketcap 发表了一篇名为“Zebec 模块化 Layer3 链 Nautilus Chain上线主网,为 DeFi 和流支付的未来构建基础”的文章,文中对 Zebec 生态公链 Nautilus Chain 的生态进展进行了简要的报道,并对其进行了…...

java设计模式之命令设计模式的前世今生
命令设计模式是什么? 命令设计模式是一种行为型设计模式,它允许将请求封装为对象,并将其传递给调用者,从而使调用者可以在不知道请求具体细节的情况下进行操作。命令模式的主要目的是解耦请求的发送者和接收者,以及通…...
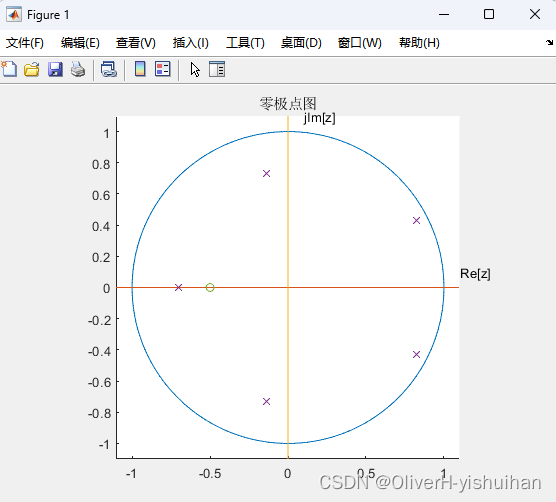
离散系统函数零积点分析
离散系统函数零积点分析 在 Matlab中,系统函数的零极点就可以通过函数 roots 得到。 函数的零极点也可以通过函数 tf2zp 获得,其调用格式为:[Z, P, K] tf2zp(B, A),函数 tf2zp 可以将H(z)的有理分式转换为零极点增益形式&#…...

Karl Guttag:苹果VST MR头显也无法突破AR的物理局限
据近期的爆料、传闻显示,苹果将6月份的WWDC2023上首次公布AR/VR头显。对此,AR/VR光学专家Karl Guttag持怀疑态度,他此前在DisplayDaily的文章中写道,苹果研发AR/VR头显更像是担心错过新技术趋势。回顾过去的一些关键的AR产品&…...
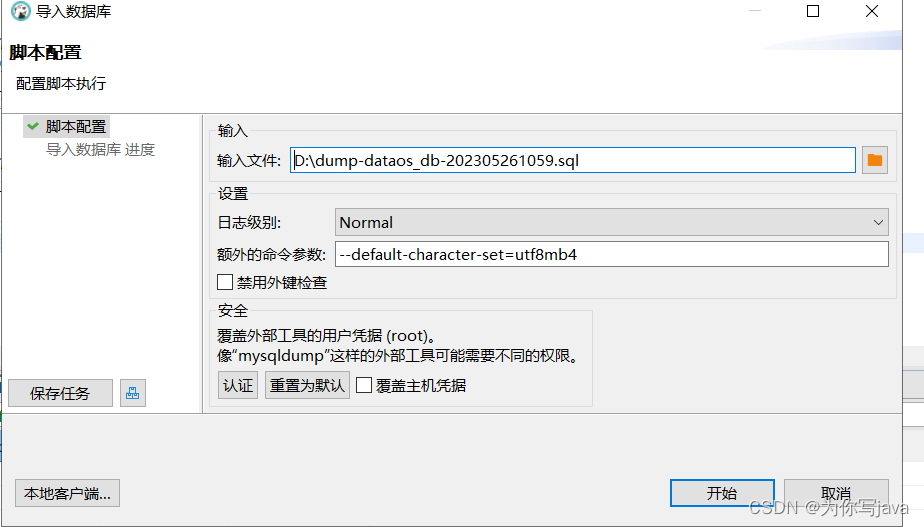
mysql倒库操作遇到的问题
背景:本地windows 10安装了mysql数据库后,需要把远程库的表结构和数据全部导入进来。 操作:导出数据库,导入数据库。 第一步:导出数据库 使用dump命令即可。 登陆mysql数据库 mysql -hhost --default-character-s…...
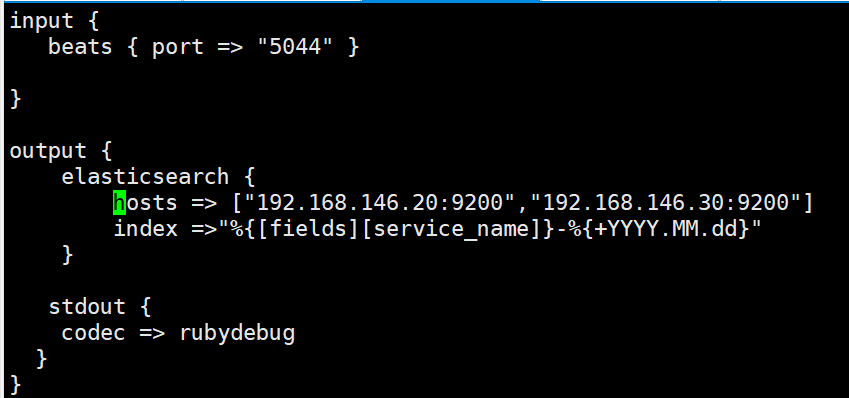
ELK企业级日志分析系统
ELK概述 为什么要使用 ELK 日志主要包括系统日志、应用程序日志和安全日志。系统运维和开发人员可以通过日志了解服务器软硬件信息、检查配置过程中的错误及错误发生的原因。经常分析日志可以了解服务器的负荷,性能安全性,从而及时采取措施纠正错误。 …...

华为OD机试真题 Java 实现【基站维修工程师】【2023Q1 200分】,附详细解题思路
一、题目描述 小王是一名基站维护工程师,负责某区域的基站维护。 某地方有n个基站(1<n<10),已知各基站之间的距离s(0<s<500),并且基站x到基站y的距离,与基站y到基站x的距离并不一定会相同。 小王从基站1出发,途径每个基站1次,然后返回基站1,需要请你…...

SSM 如何使用 TCC 机制实现分布式事务?
SSM 如何使用 TCC 机制实现分布式事务? 分布式事务是现代分布式系统中必不可少的一部分,而 TCC 机制(Try-Confirm-Cancel)是一种常用的分布式事务处理方式。在 SSM 框架中,我们可以使用 TCC 机制来管理分布式事务。本…...
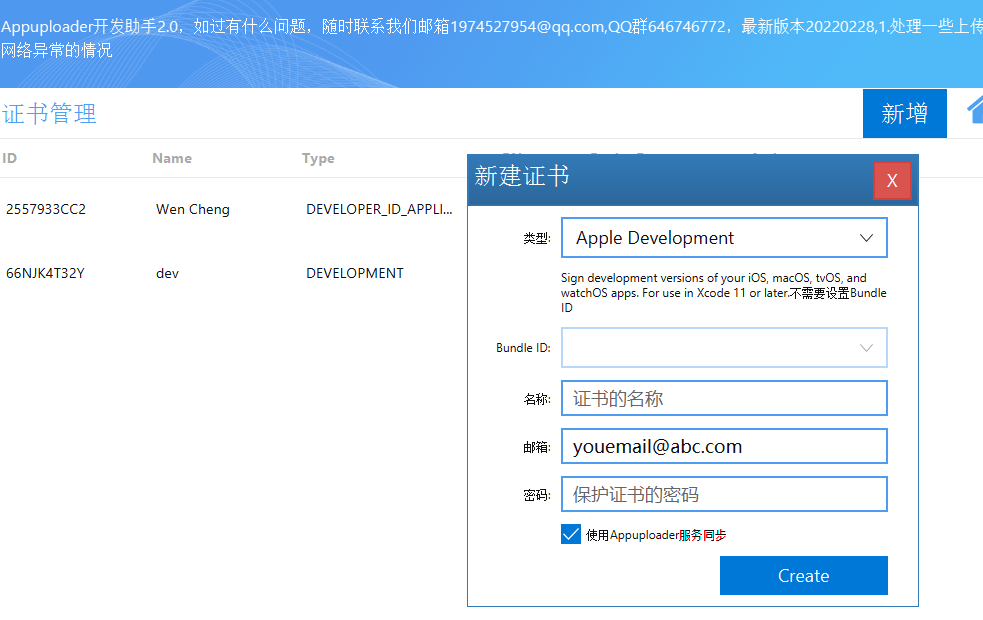
如何在上架App之前设置证书并上传应用
App上架教程 在上架App之前想要进行真机测试的同学,请查看《iOS- 最全的真机测试教程》,里面包含如何让多台电脑同时上架App和真机调试。 P12文件的使用详解 注意: 同样可以在Build Setting 的sign中设置证书,但是有点麻烦&…...

华清远见 day04
break 打破循环,再也不执行 continue 跳出本次循环,继续执行下一次循环; 常量 字面常量 宏常量 #define A 100 //定义一个宏常量, 名为:A 值为:100 位置 在 头文件 下面 ,文件开头 输入时间秒 得到 小时 分钟 秒的时间输出 用到 三运算符; 宏常量 Mi 是60 t1 /Mi>6…...

如何处理Vue应用程序中的错误和异常情况?
处理Vue应用程序中的错误和异常情况是开发中非常重要的一环,但是对于新手来说,这往往是一个比较棘手的问题。不过别担心,下面我将为大家详细解答。 首先,我们需要知道的是,在Vue中,错误和异常情况是两个不…...

javascript基础十六:Ajax 原理是什么?如何实现?
一、是什么 AJAX全称(Async Javascript and XML) 即异步的JavaScript 和XML,是一种创建交互式网页应用的网页开发技术,可以在不重新加载整个网页的情况下,与服务器交换数据,并且更新部分网页 Ajax的原理简单来说通过XmlHttpRequ…...

大话手游原始服务端搭建教程Centos
大话手游原始服务端搭建教程Centos 大家好,我是艾西,今天给大家分享一款回合制的ARPG大话手游搭建教程。游戏场景、精美的画面以及多元的人物做的非常棒。在游戏中可以穿越神话世界,同时也可以结交好友,加入团队,共同…...

C语言中的通用工具库stdlib.h
目录 1、malloc和free:用于动态内存分配和释放。 2、atoi和atof:用于将字符串转换为整数或浮点数。 3、rand和srand:用于生成随机数和设置随机数种子。 4、system:用于执行系统命令。 5、exit:用于退出程序。 6、…...
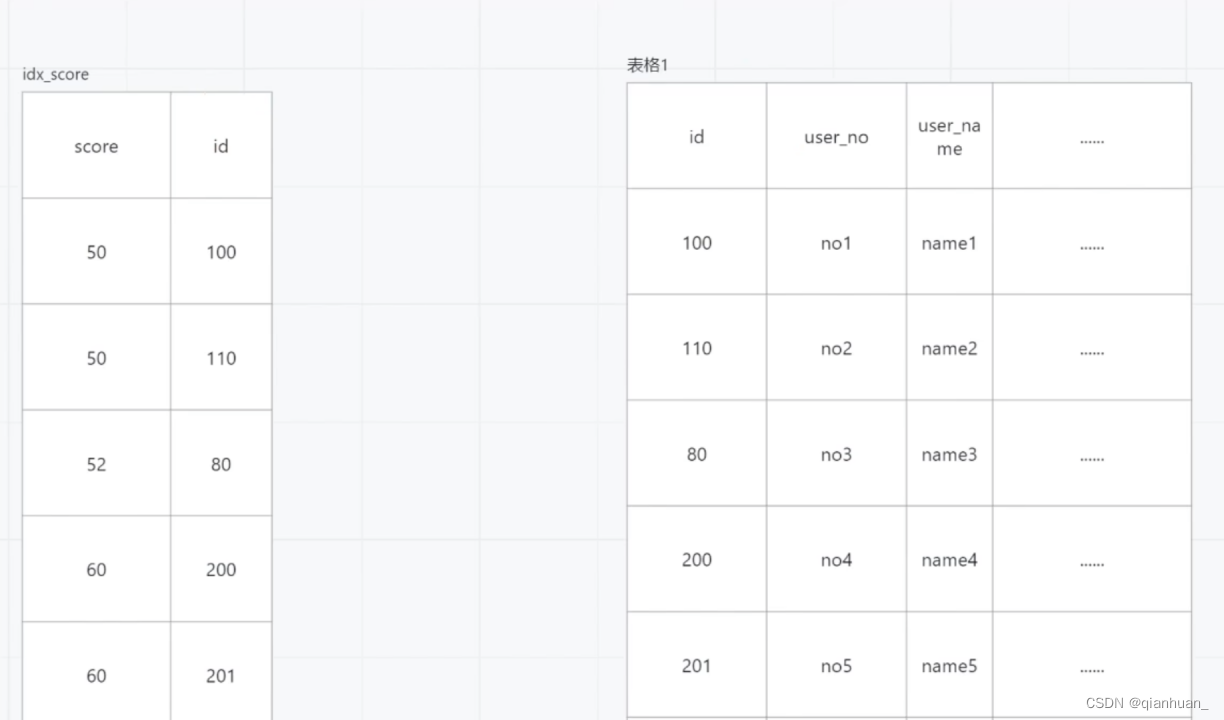
优化带排序的分页查询
优化带排序的分页查询 浅分页: select user_no,user_name,socre from student order by score desc limit 5,20 深分页: select user_no,user_name,socre from student order by score desc limit 80000,20 因为偏移量深分页更大,所以深分页执…...

chatgpt赋能python:Python如何删除空白
Python 如何删除空白 在SEO优化过程中,我们需要保证我们的网页内容的质量和可读性。其中,一个重要的因素是删除空白。在Python中,我们可以使用多种方法来删除空白,下面我们将介绍一些方法并讨论它们的优缺点。 方法一࿱…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

大模型——基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程
基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网:https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘,大小大概2.9G,做这行最忌讳的就是安装软件全装C盘,所以我调整了下安装路径。 新建安装目录:E:\MyS…...
