Sangria:类似Nova folding scheme的relaxed PLONK for PLONK
1. 引言
前序博客有:
- Nova: Recursive Zero-Knowledge Arguments from Folding Schemes学习笔记
- SuperNova:为多指令虚拟机执行提供递归证明
- 基于Nova/SuperNova的zkVM
- Sangria:PLONK + Folding
- 2023年 ZK Hack以及ZK Summit 亮点记
主要见2023年4月 Geometry团队Nicolas Mohnblatt在- Zero Knowledge Summit 9 on April 4 2023 in Lisbon 会议上的分享视频:
- ZK9: Sangria is relaxed PLONK a Nova-like folding scheme for PLONK – Nicolas Mohnblatt (Geometry)
- Nico 2023年3月twitterSNARK recursion survey
微软团队2021年论文 《Nova: Recursive Zero-Knowledge Arguments from Folding Schemes》中首次提出了Folding schemes:
- 将某problem的2个instance 压缩为 同一问题的single instance。如解决了2个数独题,无需展示2个答案,而可以将其合并展示为1个答案。
Folding schemes为实现cheap recursion的关键要素。在Nova论文中仅展示了针对R1CS电路的folding scheme。而Sangria为针对PLONKish电路的folding scheme。
Sangria的开销与Nova的类似:
- Verifier work为常量值,与电路中的行数(即depth)无关
- 引入的常量值开销要比Nova大,但是该代价 带来的好处是 可获得更灵活的arithmetization。
当前Lurk项目在使用Nova方案,详细见Lurk——Recursive zk-SNARKs编程语言。
Sangria也在与相关项目方做相关实现。
2. 为何需要递归,以及现有递归方案
2.1 为何需要递归?——IVC
为何需要递归?
其目的是为了实现 IVC(Incrementally Verifiable Computation)。
对于需要将某函数 F F F执行 n n n次的长计算:

Prover想要证明其知道private inputs w 0 , w 1 , ⋯ , w n − 1 w_0,w_1,\cdots,w_{n-1} w0,w1,⋯,wn−1,使得由初始状态 s 0 s_0 s0执行 n n n次 F F F函数之后, s n s_n sn为正确的最终状态。
实际上,IVC可用于构建:
- zkVMs:可将 F F F函数看成是(如RISC、ARM等)微处理器的一个cycle,对 F F F函数的迭代执行可看成是处理器的运行。
- rollups:将 s s s看成是区块链状态, w w w为incoming交易, F F F为表示区块链状态变化的transition function。rollup可为很多很多区块构建succinct proof。
- VDF(Verifiable Delay Functions):如Open VDF: Accelerating the Nova SNARK-based VDF。
为实现IVC,定义某Prover P F \mathcal{P}_F PF,其输入有某state和某proof,输出为更新的state和更新的proof:

从而可将Prover P F \mathcal{P}_F PF的内部结构拆分为2部分表示:
- 1)函数 F F F:输入某state,执行 F F F函数,输出更新的state。
- 2)overhead:输入某proof,运行overhead,输出更新的proof。overhead主要工作为Verifier验证前一proof,并为 该验证过程的正确执行 生成新的proof。

为实现IVC Prover P F \mathcal{P}_F PF: - 需要一些额外的开销来更新proof。这些额外的开销在IVC的每一个step都需要,关键怎么将这些额外的开销做到最低。
2.2 现有IVC方案对比
现有的IVC方案在实现overhead上主要分为:
-
1)SNARK of SNARK:Verifier会读取整个proof,并验证整个proof,无任何延缓操作。【每个step都需要读取完整的proof,并验证完整的proof。】
SNARK of SNARK代表方案有:- Plonky2:为recursive STARK。 2 12 2^{12} 212个gate,不过为wide gate——width of 135 (Goldilocks) elements,且conjectured FRI soundness约为100 bits。
- Fractal:为Groth16 + [BCTV14](2013年论文Succinct Non-Interactive Zero Knowledge for a von Neumann Architecture)。
Fractal很昂贵,有约百万级的R1CS约束。
-
2)Accumulation(atomic)(原子式累加):Verifier会读取整个proof,但只验证部分,会将hard part的验证累加推迟,即递归 n n n次,仅需要对hard part做一次验证。【每个step都需要读取完整的step,并做部分验证,在最后一个step需对hard part进行一次验证即可。】
Accumulation(atomic)(原子式累加)代表方案有:- Halo/Halo2 以及 [BCMS20](对应2020年论文Proof-Carrying Data from Accumulation Schemes):约束数为数十万——优于SNARK of SNARK的百万级约束。

- Halo/Halo2 以及 [BCMS20](对应2020年论文Proof-Carrying Data from Accumulation Schemes):约束数为数十万——优于SNARK of SNARK的百万级约束。
-
3)Accumulation(split)(切分累加):Verifier会读取部分proof,但只验证部分,会将hard part的验证累加推迟,即递归 n n n次,仅需在最后读取一次完整的proof,并对hard part做一次验证。【每个step仅需读取部分proof,并做部分验证,仅需在最后一个step读取一次完整的proof,并执行一次hard part验证。】
Accumulation(split)(切分累加)代表方案有:- [BCLMS21]对应2020年论文Proof-Carrying Data without Succinct Arguments:其牺牲了succinctness。
-
4)Folding:读取unproven instance,将其压缩为a running instance,对proving进行推迟。【每个step读取unproven instance,执行 F F F来获得new running instance,只在最后一个step做证明】
Folding代表方案有:- Nova:比之前方案的overhead开销要便宜很多,仅有约2万个约束。

Sangria关注的点在于,在Nova的基础上,将R1CS电路表示,替换为效率更高的PLONK电路表示。
3. PLONK folding scheme设计思路
3.1 PLONK Arithmetization定义

PLONK trace与Sudoku(数独)类似:
-
具有固定size的网格
-
向单元格内填充“数字(有限域)”
-
有某些已填值:这些已填值为selectors和public inputs。

-
需遵循一系列rules规则:
- 规则 #1:copy constraints:

- 规则 #2:用于每行的gate equation:
( q L ) i a i + ( q R ) i b i + ( q O ) i c i + ( q M ) i a i b i + ( q C ) i = 0 (q_L)_ia_i+(q_R)_ib_i+(q_O)_ic_i+(q_M)_ia_ib_i+(q_C)_i=0 (qL)iai+(qR)ibi+(qO)ici+(qM)iaibi+(qC)i=0
- 规则 #1:copy constraints:
-
根据selectors和rules即定义了某circuit。
-
整个trace可分为:
- instance X:公开信息,对Prover和Verifier均已知。
- witness W:private信息,仅对Prover已知。

3.2 Folding Scheme定义
folding scheme是将相同电路的2个instance压缩为1个instance,具体定义见ZKMOOC中的下图:

folding schem需满足:
- completeness属性
- knowledge soundness属性
注意Folding scheme不是argument,folding scheme中不证明任何东西,Verifier接收后直接进入下一step——这也是为啥folding scheme更cheaper的理论原因。
3.3 PLONK folding scheme设计方案一
PLONK folding scheme设计方案一:
- 采用密码学家最好的朋友:
- random linear combination

- random linear combination
引入随机值 r r r,random linear combination之后:
- Copy constraints仍然成立。
- gate equation为非线性的,会存在一些问题。
3.4 PLONK folding scheme设计方案二
Nova采用了相应的方案:
- 对gate equation进行relaxed
- Prover对整个trace进行操作,而Verifier操作相应的commitments。commitments值很短,即意味着Verifier仅需做少量工作。
借鉴Nova,PLONK folding scheme设计方案二为——Relaxed PLONK arithmetization:
- Witness(私有信息):包括:
- PLONK witness: W = ( w a , w b , w c ) \mathbf{W}=(\mathbf{w}_a,\mathbf{w}_b,\mathbf{w}_c) W=(wa,wb,wc)
- 某error vector: e \mathbf{e} e
- Instance(公开信息):包括:
- public inputs: X = ( x a , x b , x c ) \mathbf{X}=(\mathbf{x}_a,\mathbf{x}_b,\mathbf{x}_c) X=(xa,xb,xc)
- 某scalar值: u u u
- 以上witness的承诺值:【图片中以方框来表示承诺值】
C o m ( w a ) , C o m ( w b ) , C o m ( w c ) , C o m ( e ) Com(\mathbf{w}_a),Com(\mathbf{w}_b),Com(\mathbf{w}_c), Com(\mathbf{e}) Com(wa),Com(wb),Com(wc),Com(e)
- Relaxed gate equation:【即Sangria的名字来源】
u [ ( q L ) i a i + ( q R ) i b i + ( q O ) i c i ] + ( q M ) i a i b i + u 2 ( q C ) i + e i u[(q_L)_ia_i+(q_R)_ib_i+(q_O)_ic_i]+(q_M)_ia_ib_i+u^2(q_C)_i+e_i u[(qL)iai+(qR)ibi+(qO)ici]+(qM)iaibi+u2(qC)i+ei
这样,上述多项式中除 e i e_i ei之外的各项的degree均为2,从而实现了homogeneous函数。 e i e_i ei作为error项,功能类似可扔的trash,包含了所不想要的内容。
然后仍然引入随机值 r r r,random linear combination之后,folding为:

将folding之后的值插入到relaxed gate equation中,有:

其中 t \mathbf{t} t为something big and ugly。
根据folding scheme中的completeness属性,若trace正确,则Gate之后值为0,从而有 G a t e ( t r a c e ′ ) = 0 , G a t e ( t r a c e ′ ′ ) = 0 Gate(trace')=0,Gate(trace'')=0 Gate(trace′)=0,Gate(trace′′)=0,剩下的为ugly r t r\mathbf{t} rt。
为摆脱ugly t \mathbf{t} t,可借助上面定义的trash error term e \mathbf{e} e,并将其folding为:
e = e ′ − r t + r 2 e ′ ′ \mathbf{e}=\mathbf{e}'-r\mathbf{t}+r^2\mathbf{e''} e=e′−rt+r2e′′
3.5 PLONK folding scheme设计方案:Sangria
若gate equation为固定的,则 t \mathbf{t} t也是固定的。
因此:
-
在协议开始之初,Prover可计算 t \mathbf{t} t,并将其承诺值发送给Verifier。
-
Verifier发送随机值 r r r。
-
Prover:
- 计算trace的random linear combination。
Verifier:
- 计算public inputs的random linear combination。
- 计算各witness承诺值的random linear combination。【承诺方案应具有加法同态属性。】
整个交互流程为:【为简化表述,忽略了hiding需求。】

Sangria论文中的各变量的具体值为:【可看出各个变量的值很复杂,ugly。且在论文中考虑了hiding需求。】

4. Sangria性能分析——即overhead开销
Sangria性能分析——即overhead开销,Verifier的主要工作为承诺值的加法运算:【包含5次point addition运算】

实际上,是将 一个standard PLONK instance folding为 一个relaxed PLONK instance:
- standard PLONK instance中没有error项
- Verifier仅需做4次point addition运算。比5次少一次的原因在于:
在实际做IVC时,incoming instance并未relaxed,因此其没有narrow term,所以实际上仅需要4次point addition运算。
因此:
- Sangria overhead的开销为4次point addition运算。
- 而Nova的overhead开销仅为2次point addition运算。Nova方案要更简洁,因为其不需要处理3个witness承诺值,Nova仅需要处理1个witness承诺值。
但Sangria具有更大的灵活性——采用PLONK电路:
- 可添加更多的列
- 可修改gate equation
5. TurboPLONK对Sangria性能的影响
Sangria具有更大的灵活性——采用PLONK电路:
- 1)可添加更多的列(Wider Circuits):
当使用Sangria folding scheme处理wider circuits时,需对每额外增加的列做commit,相应的开销为:【所谓wider circuits,是指具有larger fan-in fan-out at each gate的电路。即gate中多于2个in wire,多于1个out wire的情况。】- 每额外增加一个trace列,Verifier需额外多做一次point addition运算。
- 2)可修改gate equation(Custom Gates):
当使用Sangria folding scheme处理custom Gates(higher degree Gates)时:- degree为 d d d的gate,将relaxed with powers of u u u up to u d u^d ud。
- error的folding equation形如:
e = e ′ − r t 1 − r 2 t 2 − ⋯ − r d − 1 t d − 1 + r d e ′ ′ \mathbf{e}=\mathbf{e}'-r\mathbf{t}_1-r^2\mathbf{t}_2-\cdots - r^{d-1}\mathbf{t}_{d-1}+r^d\mathbf{e''} e=e′−rt1−r2t2−⋯−rd−1td−1+rde′′ - 相应的开销为:
- degree每额外加1:Prover的message中需额外包含一个新的承诺值,Veriifer需额外多做一次point addition运算。
6. 设计空间——递归开销的最小值
设计递归证明方案的关键在于:
- 如何让overhead开销最小化

当前,Nova电路有约2万个约束,其中1.2万个为point addition。
开放问题为:
- 对本文第5章的场景,采用wider circuits和custom gates的优势,能否超过给folding Verifier引入额外point additions运算开销的劣势?即如何在递归overhead开销 与 电路灵活性 之间权衡?
7. 后续工作
后续安排有:
- Sangria为对标Nova的PLONK folding scheme,未来可能有对标SuperNova的PLONK folding scheme。
- 当前正在做standard PLONK的Sangria代码实现。
- 针对ultraPLONK,lookup-enabled traces的folding scheme。
- 可能的非凡电路表示:具有cheaper overhead和super cheap IVC。
相关文章:

Sangria:类似Nova folding scheme的relaxed PLONK for PLONK
1. 引言 前序博客有: Nova: Recursive Zero-Knowledge Arguments from Folding Schemes学习笔记SuperNova:为多指令虚拟机执行提供递归证明基于Nova/SuperNova的zkVMSangria:PLONK Folding2023年 ZK Hack以及ZK Summit 亮点记 主要见2023…...

【蓝桥杯省赛真题22】python剩余空间问题 青少年组蓝桥杯比赛python编程省赛真题解析
目录 python剩余空间问题 一、题目要求 1、编程实现 二、解题思路...

基于深度学习的高精度牙齿健康检测识别系统(PyTorch+Pyside6+YOLOv5模型)
摘要:基于深度学习的高精度牙齿健康检测识别系统可用于日常生活中检测牙齿健康状况,利用深度学习算法可实现图片、视频、摄像头等方式的牙齿目标检测识别,另外支持结果可视化与图片或视频检测结果的导出。本系统采用YOLOv5目标检测模型训练数…...

C++的类
类的性质 上文的例子中用到了类,也知道了类的定义方法,其实类还有更多的性质,这些更多的性质完整支持了面向对象编程。 封装 以前说过,程序就是数据和代码的组合。而C又正好提供了对数据的封装功能,这就可以很好的完…...

【网络】- TCP/IP四层(五层)协议 - 网际层(网络层) - 划分子网、构造超网
目录 一、概述二、分类IP地址不合理的地方三、划分子网四、无分类编址方法 一、概述 前面的文章介绍了网络层的网际协议IP,介绍了IP地址的定义,知道了IP地址分为网络标识(网络地址)、主机标识(主机地址)两部分,也清楚了最初IP地址是按照分类被…...
1-网络初识——网络发展史
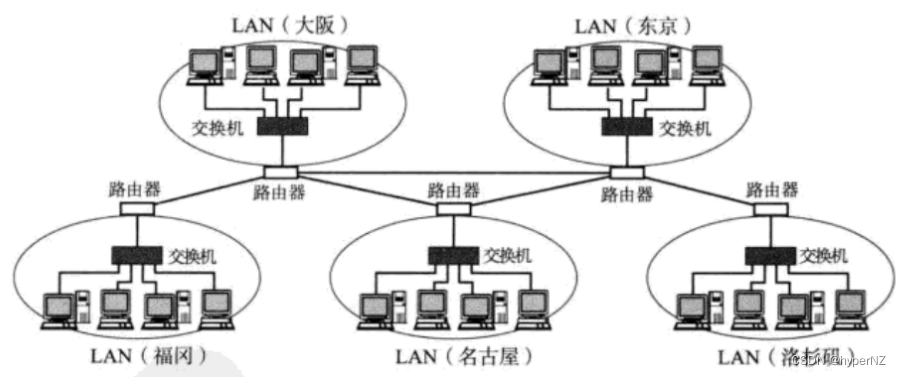
目录 1.独立模式 2.网络互联 2.1.局域网(Local Area Network,简称LAN) ①基于网线直连 ②基于集线器组建 ③基于交换机组建 ④基于交换机(网口很多)和路由器组建 2.2.广域网(Wide Area Network&…...
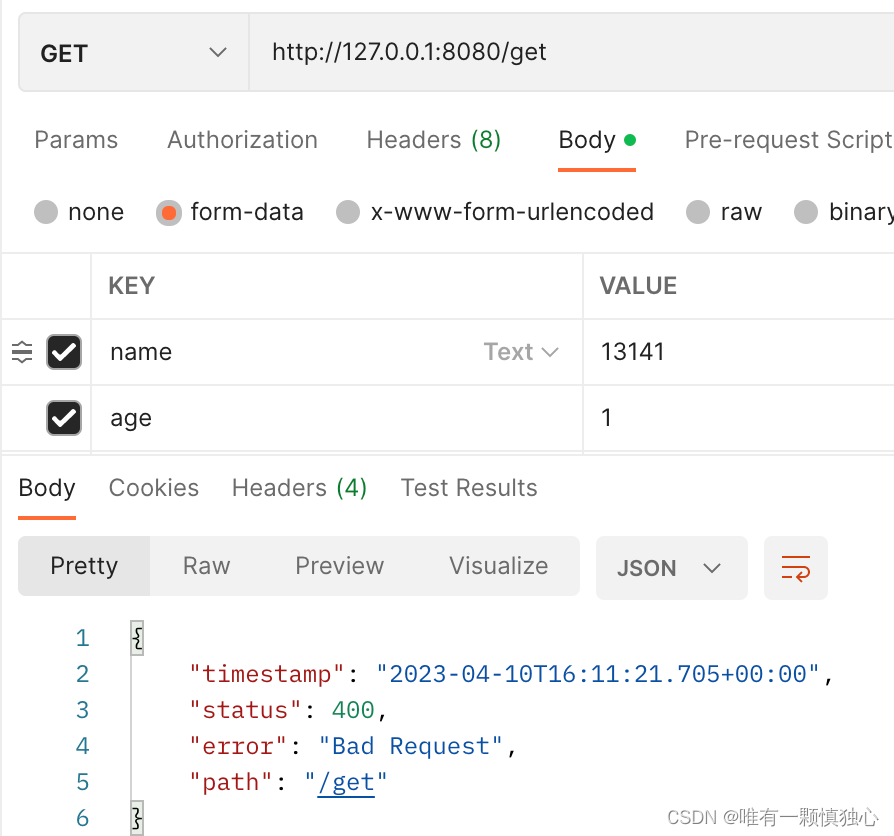
《Spring Guides系列学习》guide35 - guide40
要想全面快速学习Spring的内容,最好的方法肯定是先去Spring官网去查阅文档,在Spring官网中找到了适合新手了解的官网Guides,一共68篇,打算全部过一遍,能尽量全面的了解Spring框架的每个特性和功能。 接着上篇看过的gu…...

《算法导论》拓展之 一维二维最近点对问题
一维点对问题 描述:一维最近点对问题是指在给定的一维点集中找到距离最近的两个点。具体来说,给定一维坐标轴上的 n 个点,要找出其中的两个点,使它们的距离最小。 解决办法:解决这个问题的一种常见方法是使用排序和线…...

【C++】动态存储分配
动态存储分配是指在程序运行时根据需要动态地分配和释放内存空间。 C中提供了两个关键的运算符用于动态存储分配:new和delete。 使用new运算符可以在堆(heap)上动态地分配内存空间,并返回所分配内存的首地址。语法如下࿱…...
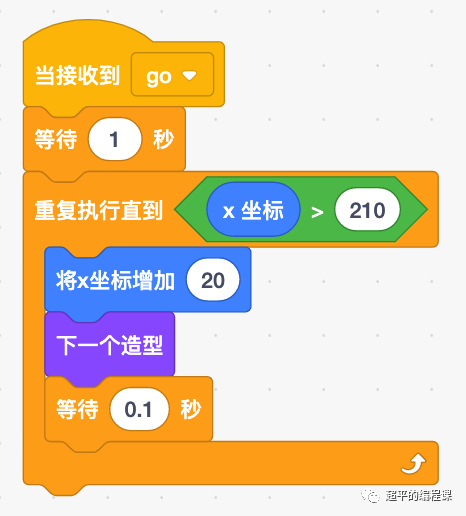
小狗避障-第14届蓝桥杯省赛Scratch中级组真题第4题
[导读]:超平老师的《Scratch蓝桥杯真题解析100讲》已经全部完成,后续会不定期解读蓝桥杯真题,这是Scratch蓝桥杯真题解析第139讲。 小狗避障,本题是2023年5月7日举行的第14届蓝桥杯省赛Scratch图形化编程中级组编程第4题…...
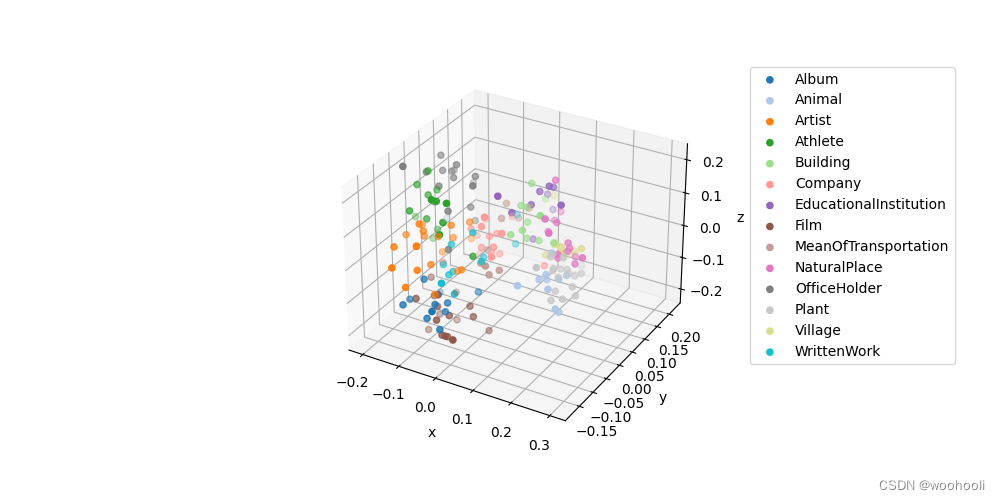
GPT学习笔记-Embedding的降维与2D,3D可视化
嵌入(Embedding)在机器学习和自然语言处理中是一种表示离散变量(如单词、句子或整个文档)的方式,通常是作为高维向量或者矩阵。嵌入的目标是捕捉到输入数据中的语义信息,使得语义相近的元素在嵌入空间中的距…...

Nautilus Chain上线主网,为DeFi和流支付的未来构建基础
近日,加密行业权威平台 Coinmarketcap 发表了一篇名为“Zebec 模块化 Layer3 链 Nautilus Chain上线主网,为 DeFi 和流支付的未来构建基础”的文章,文中对 Zebec 生态公链 Nautilus Chain 的生态进展进行了简要的报道,并对其进行了…...

java设计模式之命令设计模式的前世今生
命令设计模式是什么? 命令设计模式是一种行为型设计模式,它允许将请求封装为对象,并将其传递给调用者,从而使调用者可以在不知道请求具体细节的情况下进行操作。命令模式的主要目的是解耦请求的发送者和接收者,以及通…...
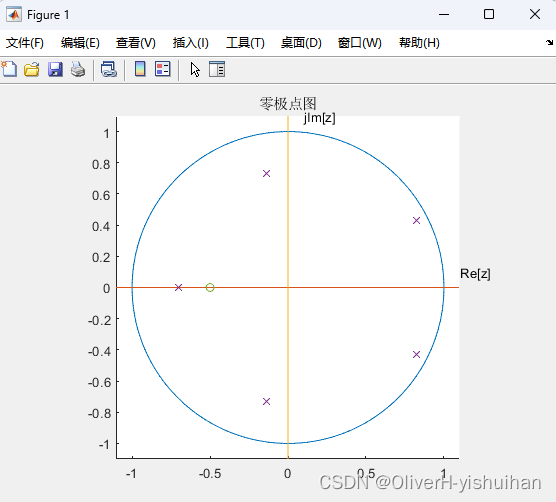
离散系统函数零积点分析
离散系统函数零积点分析 在 Matlab中,系统函数的零极点就可以通过函数 roots 得到。 函数的零极点也可以通过函数 tf2zp 获得,其调用格式为:[Z, P, K] tf2zp(B, A),函数 tf2zp 可以将H(z)的有理分式转换为零极点增益形式&#…...

Karl Guttag:苹果VST MR头显也无法突破AR的物理局限
据近期的爆料、传闻显示,苹果将6月份的WWDC2023上首次公布AR/VR头显。对此,AR/VR光学专家Karl Guttag持怀疑态度,他此前在DisplayDaily的文章中写道,苹果研发AR/VR头显更像是担心错过新技术趋势。回顾过去的一些关键的AR产品&…...
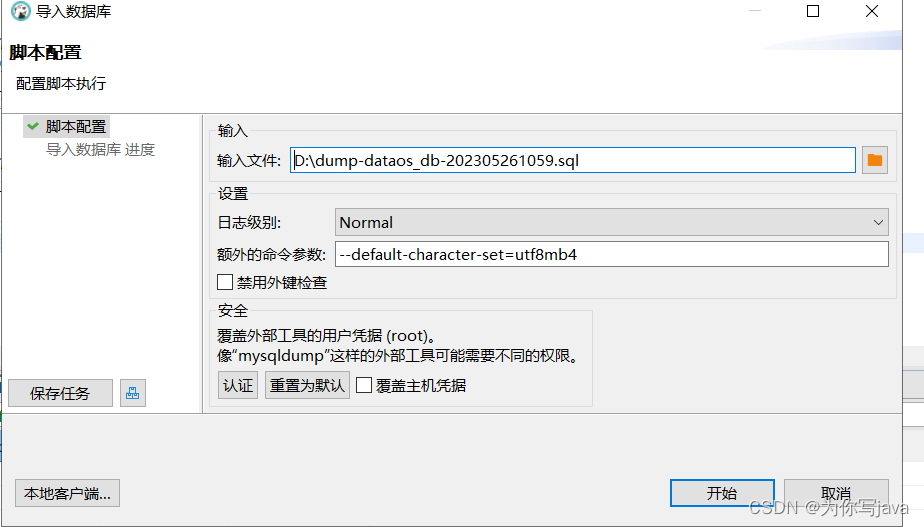
mysql倒库操作遇到的问题
背景:本地windows 10安装了mysql数据库后,需要把远程库的表结构和数据全部导入进来。 操作:导出数据库,导入数据库。 第一步:导出数据库 使用dump命令即可。 登陆mysql数据库 mysql -hhost --default-character-s…...
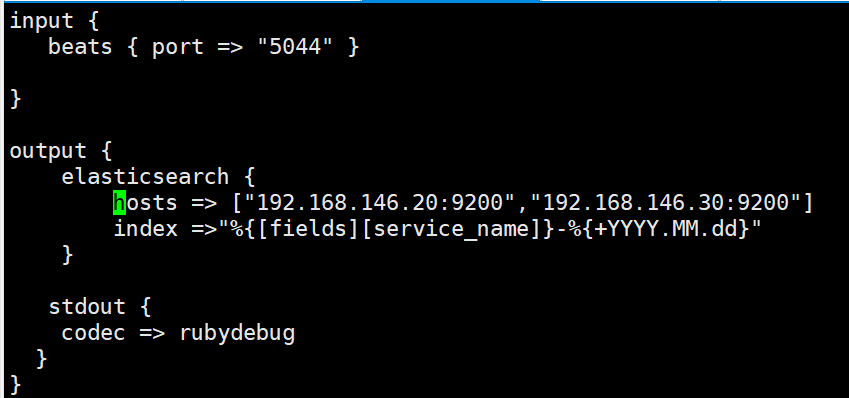
ELK企业级日志分析系统
ELK概述 为什么要使用 ELK 日志主要包括系统日志、应用程序日志和安全日志。系统运维和开发人员可以通过日志了解服务器软硬件信息、检查配置过程中的错误及错误发生的原因。经常分析日志可以了解服务器的负荷,性能安全性,从而及时采取措施纠正错误。 …...

华为OD机试真题 Java 实现【基站维修工程师】【2023Q1 200分】,附详细解题思路
一、题目描述 小王是一名基站维护工程师,负责某区域的基站维护。 某地方有n个基站(1<n<10),已知各基站之间的距离s(0<s<500),并且基站x到基站y的距离,与基站y到基站x的距离并不一定会相同。 小王从基站1出发,途径每个基站1次,然后返回基站1,需要请你…...

SSM 如何使用 TCC 机制实现分布式事务?
SSM 如何使用 TCC 机制实现分布式事务? 分布式事务是现代分布式系统中必不可少的一部分,而 TCC 机制(Try-Confirm-Cancel)是一种常用的分布式事务处理方式。在 SSM 框架中,我们可以使用 TCC 机制来管理分布式事务。本…...
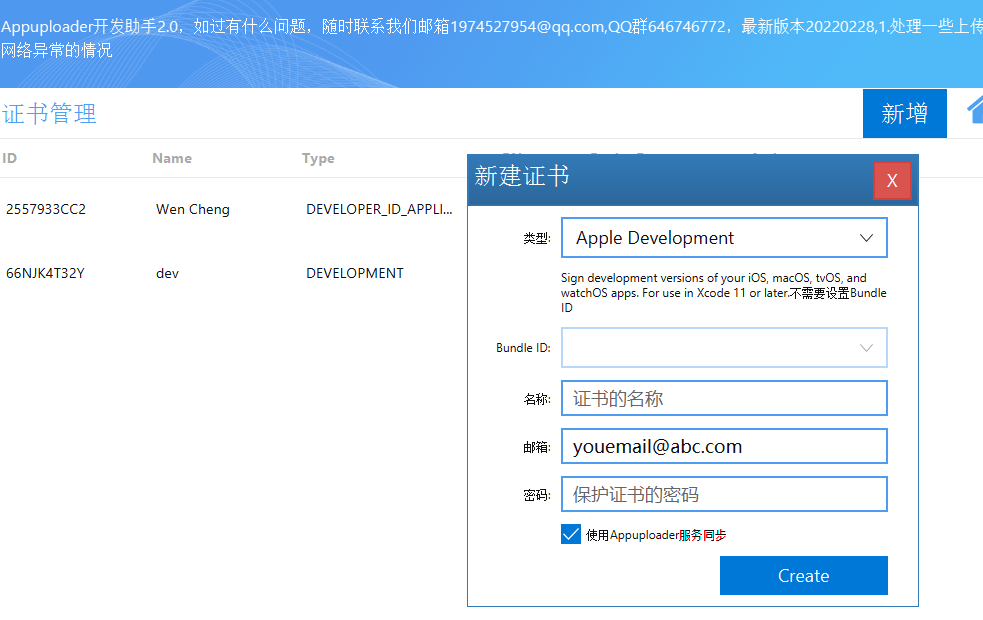
如何在上架App之前设置证书并上传应用
App上架教程 在上架App之前想要进行真机测试的同学,请查看《iOS- 最全的真机测试教程》,里面包含如何让多台电脑同时上架App和真机调试。 P12文件的使用详解 注意: 同样可以在Build Setting 的sign中设置证书,但是有点麻烦&…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
