LC-1439. 有序矩阵中的第 k 个最小数组和(二分答案、多路归并)
1439. 有序矩阵中的第 k 个最小数组和
难度困难120
给你一个 m * n 的矩阵 mat,以及一个整数 k ,矩阵中的每一行都以非递减的顺序排列。
你可以从每一行中选出 1 个元素形成一个数组。返回所有可能数组中的第 k 个 最小 数组和。
示例 1:
输入:mat = [[1,3,11],[2,4,6]], k = 5
输出:7
解释:从每一行中选出一个元素,前 k 个和最小的数组分别是:
[1,2], [1,4], [3,2], [3,4], [1,6]。其中第 5 个的和是 7 。
示例 2:
输入:mat = [[1,3,11],[2,4,6]], k = 9
输出:17
示例 3:
输入:mat = [[1,10,10],[1,4,5],[2,3,6]], k = 7
输出:9
解释:从每一行中选出一个元素,前 k 个和最小的数组分别是:
[1,1,2], [1,1,3], [1,4,2], [1,4,3], [1,1,6], [1,5,2], [1,5,3]。其中第 7 个的和是 9 。
示例 4:
输入:mat = [[1,1,10],[2,2,9]], k = 7
输出:12
提示:
m == mat.lengthn == mat.length[i]1 <= m, n <= 401 <= k <= min(200, n ^ m)1 <= mat[i][j] <= 5000mat[i]是一个非递减数组
二分查找解决第k小问题
https://leetcode.cn/problems/find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows/solution/by-lfool-w2ul/
719. 找出第 K 小的数对距离
1439. 有序矩阵中的第 k 个最小数组和
我们先明确一下原问题:「返回所有可能数组中的第 k 个最小数组和」
对于一个给定的数组和 sum,如果该数组和小了,那我们就「向右收缩」;如果该数组和大了,那我们就「向左收缩」;如果该数组和满足要求,那我们能不能找一个更小的且满足要求的数组和,所以需要继续「向左收缩」(是不是很像「寻找最左相等元素」?自信点,就是「寻找最左相等元素」)
所以「搜索对象」是什么??很明显就是「数组和」嘛!!
那「搜索范围」又是什么呢??
- 数组和最小值可以到达多少?肯定是该矩形的第一列组成的组数和嘛 (矩形每行递增)
- 数组和最大值可以到达多少?肯定是该矩形的最后一列组成的组数和嘛 (矩形每行递增)
明确了「搜索对象」和「搜索范围」,我们还需要搞清楚怎么确定数组和小了还是大了,肯定要有一个参考对象才能确定近还是远嘛
很聪明,这个参考对象就是题目给的「第 k 最小」。对于数组和 sum,小于等于该数组和的数量为 n,如果 n < k 说明数组和小了;如果 n > k 说明数组和大了
class Solution {// https://leetcode.cn/problems/find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows/solution/by-lfool-w2ul/int m, n, k;int[][] mat;int cnt = 0; // 计算小于等于当前数组和的数量public int kthSmallest(int[][] mat, int k) {this.k = k;this.mat = mat;m = mat.length;n = mat[0].length;// 搜索范围int left = 0, right = 0;for (int i = 0; i < m; i++) {left += mat[i][0];right += mat[i][n - 1];}// 把最小值设为初始值int init = left;while (left <= right) {int mid = left - (left - right) / 2;// 初始值也算一个可行解cnt = 1;dfs(0, init, mid);// 对应数组和大了,向左收缩if (cnt >= k) right = mid - 1;// 对应数组和小了,向右收缩else left = mid + 1;}return left;}// DFS 计算 小于等于 target 的数量private void dfs(int row, int sum, int target) {// 特殊情况,直接返回// sum > target:当前数组和大于 target// cnt > k:当前小于等于 target 的数量大于 k// row >= m:已经到达最后一行 (结束条件)if (sum > target || cnt > k || row >= m) return;// 不做交换dfs(row + 1, sum, target);// 分别与 [1, n-1] 交换for (int i = 1; i < n; i++) {// 更新数组和:减去「第一个元素」,加上「要交换的元素」int newSum = sum - mat[row][0] + mat[row][i];// 交换后的数组和大于 target,直接跳出循环// 原因:由于每行元素递增,所以当前元素大了,该行后面的元素肯定也大了if (newSum > target) break;// 满足要求,cnt + 1cnt++;// 搜索下一行dfs(row + 1, newSum, target);}}
}
多路归并
题解:https://leetcode.cn/problems/find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows/solution/by-lfool-z9n4/
class Solution {// 对于每次弹出队顶元素后,需要把 n 个元素入队public int kthSmallest(int[][] mat, int k) {int m = mat.length, n = mat[0].length;Set<String> set = new HashSet<>();// 构造一个最小堆PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[m] - b[m]);// init[0..m-1] 存储矩阵的一列元素的下标// init[m]存储该列的和int[] init = new int[m+1];for(int i = 0; i < m; i++){init[m] += mat[i][0];init[i] = 0;}q.offer(init);set.add(Arrays.toString(init));while(k-- > 0){int[] cur = q.poll();if(k == 0) return cur[m];// 构造处需要加入堆的元素,一共m个for(int i = 0; i < m; i++){int[] tmp = (int[])Arrays.copyOf(cur, m+1);if(tmp[i] + 1 >= n)continue; // 下标越界了tmp[m] += mat[i][tmp[i] + 1] - mat[i][tmp[i]]; // 下标i往前进,tmp[m]处增加上变化量tmp[i] += 1;String s = Arrays.toString(tmp);if(set.contains(s)) continue;q.offer(tmp);set.add(s);}}return -1;}
}
多路归并练习题
264. 丑数 II
313. 超级丑数
373. 查找和最小的 K 对数字
786. 第 K 个最小的素数分数
1508. 子数组和排序后的区间和
719. 找出第 K 小的数对距离
1439. 有序矩阵中的第 k 个最小数组和
相关文章:
)
LC-1439. 有序矩阵中的第 k 个最小数组和(二分答案、多路归并)
1439. 有序矩阵中的第 k 个最小数组和 难度困难120 给你一个 m * n 的矩阵 mat,以及一个整数 k ,矩阵中的每一行都以非递减的顺序排列。 你可以从每一行中选出 1 个元素形成一个数组。返回所有可能数组中的第 k 个 最小 数组和。 示例 1:…...

一文1000字从0到1实现Jenkins+Allure+Pytest的持续集成
一、配置 allure 环境变量 1、下载 allure是一个命令行工具,可以去 github 下载最新版:https://github.com/allure-framework/allure2/releases 2、解压到本地 3、配置环境变量 复制路径如:F:\allure-2.13.7\bin 环境变量、Path、添加 F:\…...
)
给一个有序数组生成平衡搜索二叉树(java)
给一个有序数组生成平衡搜索二叉树 给一个有序数组生成平衡搜索二叉树递归生成二叉树专题 给一个有序数组生成平衡搜索二叉树 给定一个有序的数组,用这个数组生成一个平衡搜索二叉树. 这个题还是很简单的,知道什么时平衡搜索二叉树就行了, 左边值小于头节点值,头节点值小于右边…...

【JavaSE】Java基础语法(二十二):包装类
文章目录 1. 基本类型包装类2. Integer类3. 自动拆箱和自动装箱4. int和String类型的相互转换 1. 基本类型包装类 基本类型包装类的作用 将基本数据类型封装成对象的好处在于可以在对象中定义更多的功能方法操作该数据常用的操作之一:用于基本数据类型与字符串之间的…...
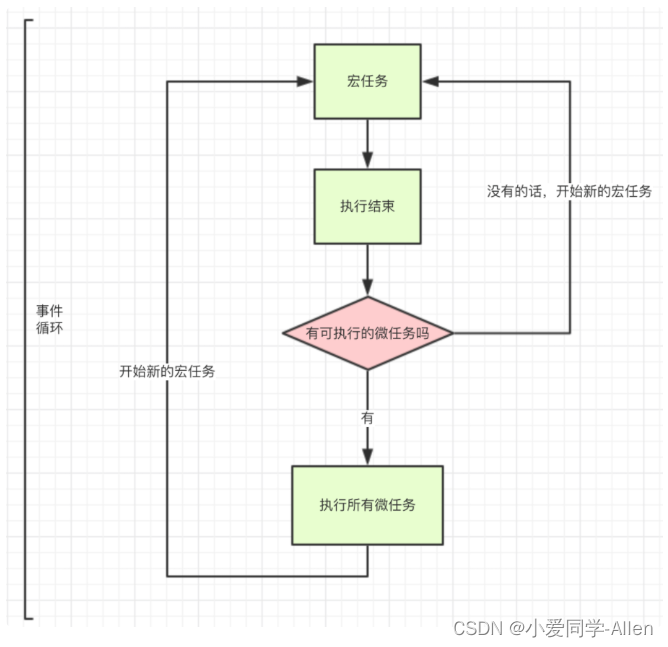
javascript基础十八:说说你对JavaScript中事件循环的理解
一、是什么 JavaScript 在设计之初便是单线程,即指程序运行时,只有一个线程存在,同一时间只能做一件事 为什么要这么设计,跟JavaScript的应用场景有关 JavaScript 初期作为一门浏览器脚本语言,通常用于操作 DOM &#…...

详解js中的浅拷贝与深拷贝
详解js中的浅拷贝与深拷贝 1、前言1.1 栈(stack)和堆(heap)1.2 基本数据类型和引用数据类型1.2.1 概念1.2.2 区别1.2.3 基本类型赋值方式1.2.4 引用类型赋值方式 2、浅拷贝2.1 概念2.2 常见的浅拷贝方法2.2.1 Object.assign()2.2.…...

Day9 敏捷测试——敏捷开发的特征、什么是敏捷测试?、极限编程、极限测试
Day9 敏捷测试——敏捷开发的特征、什么是敏捷测试?、极限编程、极限测试 文章目录 Day9 敏捷测试——敏捷开发的特征、什么是敏捷测试?、极限编程、极限测试敏捷开发的特征1、迭代式开发2、增量交付3、及时反馈4、持续集成5、自我管理敏捷开发和迭代式开发的根本区别1、性质…...

k8s 维护node与驱逐pod
1.维护node节点 设置节点状态为不可调度状态,执行以下命令后,节点状态会多出一个SchedulingDisabled的状态,即新建的pod不会往该节点上调度,本身存在node中的pod保持正常运行 kubectl cordon k8s-node01 kubectl get node 2.驱…...
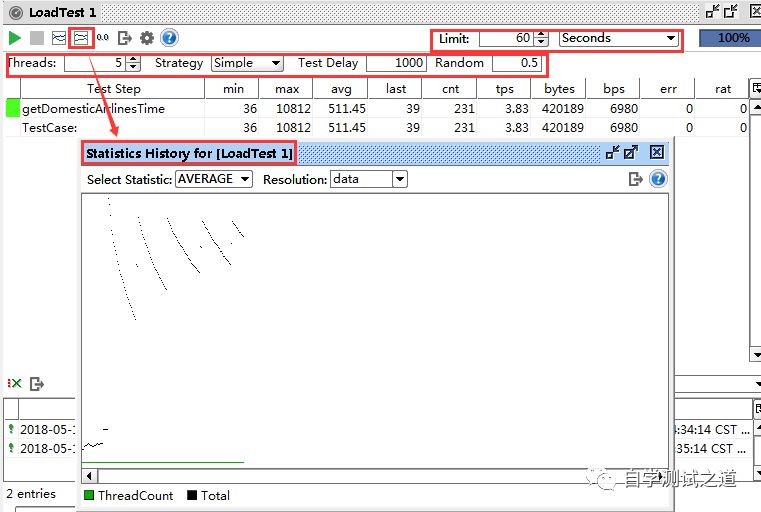
SouapUI接口测试之创建性能测试
SouapUI也是一个能生动的体现一个系统(项目)性能状态的工具,本篇就来说说如何在SouapUI工具下创建性能测试 一、创建测试用例 由于在《SouapUI接口测试之使用Excel进行参数化》篇已经创建好了测试用例,本篇就不讲解如何创建测试…...
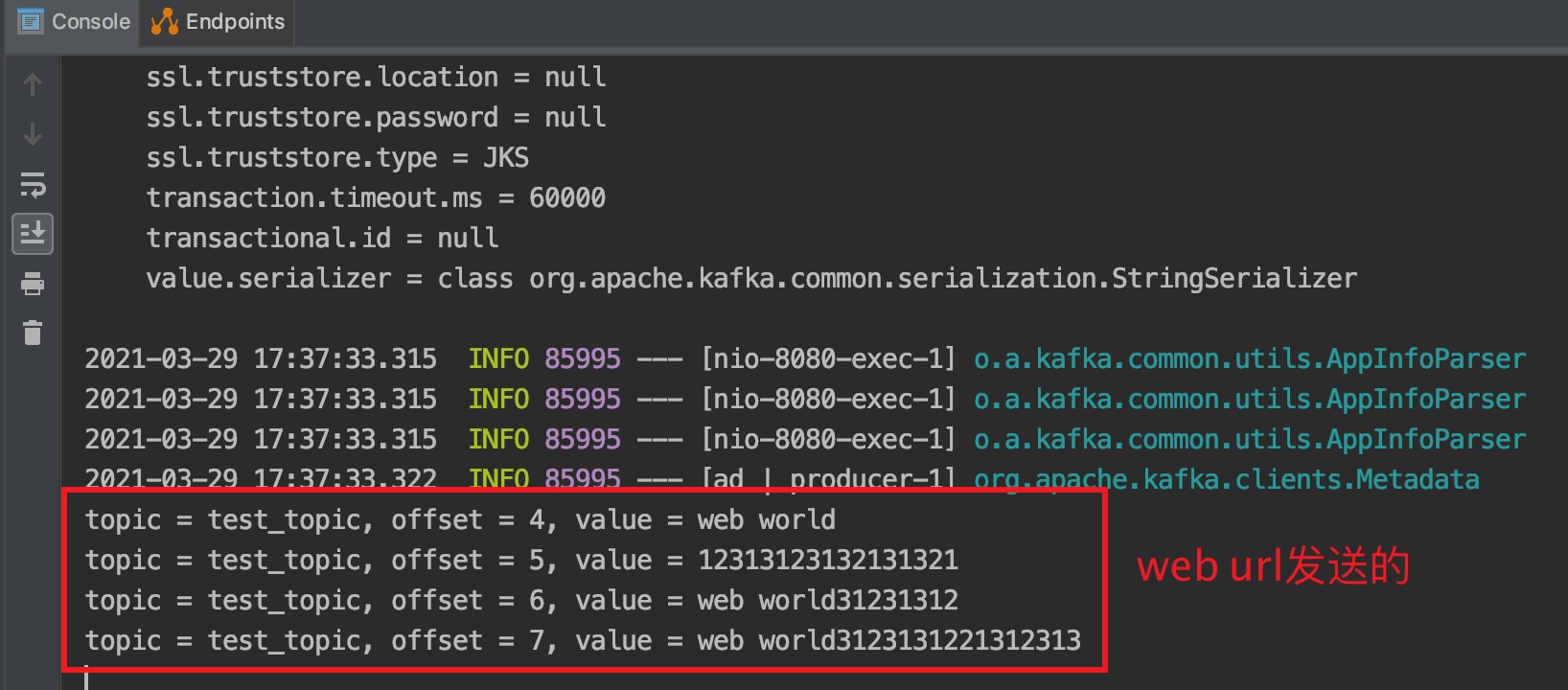
springboot整合kafka入门
kafka基本概念 producer: 生产者,负责发布消息到kafka cluster(kafka集群)中。生产者可以是web前端产生的page view,或者是服务器日志,系统CPU、memory等。 consumer: 消费者,每个consumer属于一个特定的c…...

Rust 笔记:Rust 语言中的字符串
Rust 笔记 Rust 语言中的字符串 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263?spm1001.2101.3001.5343 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/detail…...

华为OD机试真题 Java 实现【将真分数分解为埃及分数】【牛客练习题】
一、题目描述 分子为1的分数称为埃及分数。现输入一个真分数(分子比分母小的分数,叫做真分数),请将该分数分解为埃及分数。如:8/11 = 1/2+1/5+1/55+1/110。 注:真分数指分子小于分母的分数,分子和分母有可能gcd不为1! 如有多个解,请输出任意一个。 二、输入描述 输…...
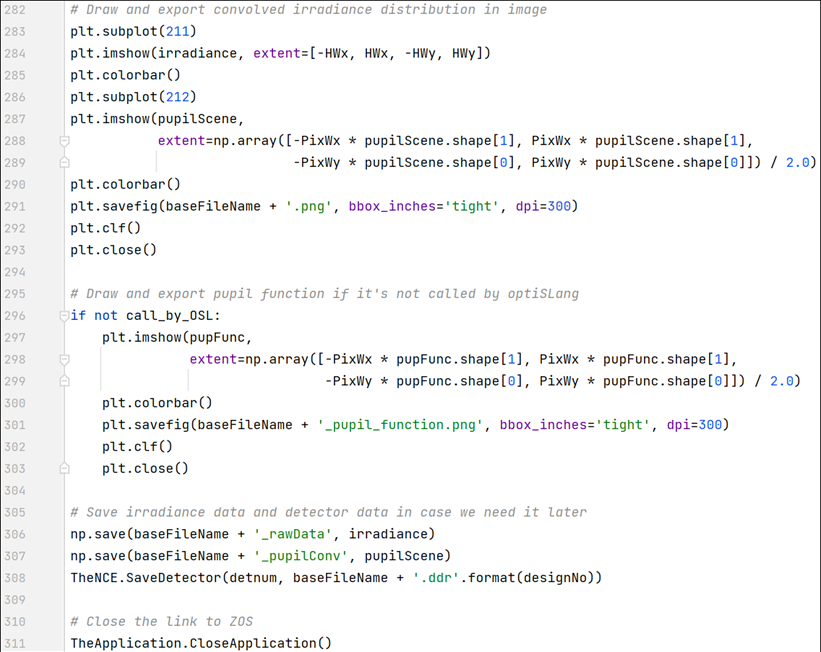
Zemax Lumerical | 二维光栅出瞳扩展系统优化
简介 本文提出并演示了一种以二维光栅耦出的光瞳扩展(EPE)系统优化和公差分析的仿真方法。 在这个工作流程中,我们将使用3个软件进行不同的工作 ,以实现优化系统的大目标。首先,我们使用 Lumerical 构建光栅模型并使用…...

Linux-0.11 文件系统read_write.c详解
Linux-0.11 文件系统read_write.c详解 模块简介 该模块实现了文件系统通用的读写的方法read/write/lseek。 根据文件类型的不同,在内部将调用不同的方法。如果是管道文件,则调用pipe.c中的读写方法,如果是字符设备,则会调用cha…...

什么是用户态和内核态?用户态切换内核态会有什么影响?
一、什么是用户态和内核态? 简单来讲,像使用java开发时,调用java中封装的普通方法程序时属于用户态,而操作内存或者cpu比如 new Thread()创建一个线程,Class.forName(xxx.class)这种属于内核态 用户态和内核态是操作系…...

探索iOS之CoreImage框架
CoreImage提供图像处理、人脸识别、图像增强、图像滤镜、图像转场。它操作的数据来自Core Graphics、Core Video、Image IO,使用CPU或GPU进行渲染。CoreImage对底层实现进行封装,为上层提供简单易用的API。 一、CoreImage框架 CoreImage框架分为&#…...

qml 使用Shape 画图形
最近在做项目的时候想这实现一个能够根据相对位置动态改变大小的进度条提示框,偶尔发现了一个很有用的组件Shape这个控件里面可以画各种线条,实线虚线矩形三角形圆角的三角形或者各种自定义形状。下面提供一个2条虚线加上一个矩形的小栗子。更多的自定义形状还是请自…...
MySQL数据库修改root账户密码
博主今天登录数据库遇到了一个问题,通过这篇文章(http://t.csdn.cn/58ECT)解决了。文中关于修改root账户密码的部分,博主觉得有必要写一篇文章总结下。 第一步:用管理员账户打开CMD 第二步:开启mysql服务 …...

基于springboot+Vue+ Element-Plus+mysql实现学生宿舍管理系统
基于springbootVue Element-Plusmysql实现学生宿舍管理系统 一、系统介绍二、功能展示1.登陆2、主页--学生3、主页--宿舍管理员4.学生管理--管理员5.宿管信息--管理员6.宿舍管理--管理员7.信息管理--管理员8.申请管理--管理员9.访客管理--管理员10.水电费管理--管理员11.卫生管…...

中国人才选拔制度演变
1、世官制 是西周时人们仍保持着牢固的宗族血缘联系,人群基本以族区分,并得到宗法封建制的制度上的保证,从而自然形成了各级宗族长同时也就是各级官长,家国一体、家国同构的统治模式、格局。换句话来讲就是我们所说的世袭制。 其…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
