周赛347（模拟、思维题、动态规划+优化）

周赛347

2710. 移除字符串中的尾随零

难度简单1

给你一个用字符串表示的正整数 num ，请你以字符串形式返回不含尾随零的整数 num 。

示例 1：

输入：num = "51230100"
输出："512301"
解释：整数 "51230100" 有 2 个尾随零，移除并返回整数 "512301" 。

示例 2：

输入：num = "123"
输出："123"
解释：整数 "123" 不含尾随零，返回整数 "123" 。

提示：

• 1 <= num.length <= 1000
• num 仅由数字 0 到 9 组成
• num 不含前导零

模拟

class Solution {public String removeTrailingZeros(String num) {int j = num.length() - 1;while(j >= 0 && num.charAt(j) - '0' == 0)j -= 1;return num.substring(0, j+1);}
}

2711. 对角线上不同值的数量差

难度中等4

给你一个下标从 0 开始、大小为 m x n 的二维矩阵 grid ，请你求解大小同样为 m x n 的答案矩阵 answer 。

矩阵 answer 中每个单元格 (r, c) 的值可以按下述方式进行计算：

• 令 topLeft[r][c] 为矩阵 grid 中单元格 (r, c) 左上角对角线上 不同值 的数量。
• 令 bottomRight[r][c] 为矩阵 grid 中单元格 (r, c) 右下角对角线上 不同值 的数量。

然后 answer[r][c] = |topLeft[r][c] - bottomRight[r][c]| 。

返回矩阵 answer 。

矩阵对角线 是从最顶行或最左列的某个单元格开始，向右下方向走到矩阵末尾的对角线。

如果单元格 (r1, c1) 和单元格 (r, c) 属于同一条对角线且 r1 < r ，则单元格 (r1, c1) 属于单元格 (r, c) 的左上对角线。类似地，可以定义右下对角线。

示例 1：

输入：grid = [[1,2,3],[3,1,5],[3,2,1]]
输出：[[1,1,0],[1,0,1],[0,1,1]]
解释：第 1 个图表示最初的矩阵 grid 。 
第 2 个图表示对单元格 (0,0) 计算，其中蓝色单元格是位于右下对角线的单元格。
第 3 个图表示对单元格 (1,2) 计算，其中红色单元格是位于左上对角线的单元格。
第 4 个图表示对单元格 (1,1) 计算，其中蓝色单元格是位于右下对角线的单元格，红色单元格是位于左上对角线的单元格。
- 单元格 (0,0) 的右下对角线包含 [1,1] ，而左上对角线包含 [] 。对应答案是 |1 - 0| = 1 。
- 单元格 (1,2) 的右下对角线包含 [] ，而左上对角线包含 [2] 。对应答案是 |0 - 1| = 1 。
- 单元格 (1,1) 的右下对角线包含 [1] ，而左上对角线包含 [1] 。对应答案是 |1 - 1| = 0 。
其他单元格的对应答案也可以按照这样的流程进行计算。

示例 2：

输入：grid = [[1]]
输出：[[0]]
解释：- 单元格 (0,0) 的右下对角线包含 [] ，左上对角线包含 [] 。对应答案是 |0 - 0| = 0 。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n, grid[i][j] <= 50

模拟

class Solution {public int[][] differenceOfDistinctValues(int[][] grid) {int m = grid.length, n = grid[0].length;int[][] res = new int[m][n];for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){Set<Integer> topleft = new HashSet<>();Set<Integer> bottomright = new HashSet<>();int k = i-1, x = j-1;while(k >= 0 && x >= 0){topleft.add(grid[k][x]);k -= 1;x -= 1;}k = i+1; x = j+1;while(k < m && x < n){bottomright.add(grid[k][x]);k += 1;x += 1;}res[i][j] = Math.abs(topleft.size() - bottomright.size());}}return res;}
}

2712. 使所有字符相等的最小成本

难度中等6

给你一个下标从 0 开始、长度为 n 的二进制字符串 s ，你可以对其执行两种操作：

• 选中一个下标 i 并且反转从下标 0 到下标 i（包括下标 0 和下标 i ）的所有字符，成本为 i + 1 。
• 选中一个下标 i 并且反转从下标 i 到下标 n - 1（包括下标 i 和下标 n - 1 ）的所有字符，成本为 n - i 。

返回使字符串内所有字符 相等 需要的 最小成本 。

反转 字符意味着：如果原来的值是 ‘0’ ，则反转后值变为 ‘1’ ，反之亦然。

示例 1：

输入：s = "0011"
输出：2
解释：执行第二种操作，选中下标 i = 2 ，可以得到 s = "0000" ，成本为 2 。可以证明 2 是使所有字符相等的最小成本。

示例 2：

输入：s = "010101"
输出：9
解释：执行第一种操作，选中下标 i = 2 ，可以得到 s = "101101" ，成本为 3 。
执行第一种操作，选中下标 i = 1 ，可以得到 s = "011101" ，成本为 2 。
执行第一种操作，选中下标 i = 0 ，可以得到 s = "111101" ，成本为 1 。
执行第二种操作，选中下标 i = 4 ，可以得到 s = "111110" ，成本为 2 。
执行第一种操作，选中下标 i = 5 ，可以得到 s = "111111" ，成本为 1 。
使所有字符相等的总成本等于 9 。可以证明 9 是使所有字符相等的最小成本。 

提示：

• 1 <= s.length == n <= 105
• s[i] 为 '0' 或 '1'

结论题（思维题）

https://leetcode.cn/problems/minimum-cost-to-make-all-characters-equal/solution/yi-ci-bian-li-jian-ji-xie-fa-pythonjavac-aut0/

class Solution:def minimumCost(self, s: str) -> int:# 结论1 ： 先选择下标1反转再反转下标2 和 先反转下标2再反转下标1 结果相同#       ==> 可以从左到右反转# 结论2 ： 当s[i-1] != s[i]时，必须反转，#               而操作：反转左边和反转右边 对[i+1:n]对答案的结果 影响相同#               或者说 反转前不同的，反转后仍然不同                        #       ==> 当s[i-1] != s[i]时，反转成本少的n = len(s)ans = 0for i in range(1, n):if s[i-1] != s[i]:ans += min(i, n-i)return ans

2713. 矩阵中严格递增的单元格数

难度困难16

给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat，你可以选择任一单元格作为 起始单元格 。

从起始单元格出发，你可以移动到 同一行或同一列 中的任何其他单元格，但前提是目标单元格的值 严格大于 当前单元格的值。

你可以多次重复这一过程，从一个单元格移动到另一个单元格，直到无法再进行任何移动。

请你找出从某个单元开始访问矩阵所能访问的 单元格的最大数量 。

返回一个表示可访问单元格最大数量的整数。

示例 1：

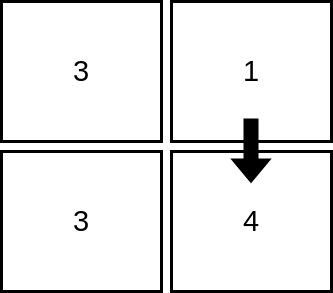
输入：mat = [[3,1],[3,4]]
输出：2
解释：上图展示了从第 1 行、第 2 列的单元格开始，可以访问 2 个单元格。可以证明，无论从哪个单元格开始，最多只能访问 2 个单元格，因此答案是 2 。 

示例 2：

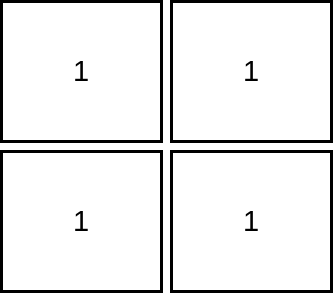
输入：mat = [[1,1],[1,1]]
输出：1
解释：由于目标单元格必须严格大于当前单元格，在本示例中只能访问 1 个单元格。 

示例 3：

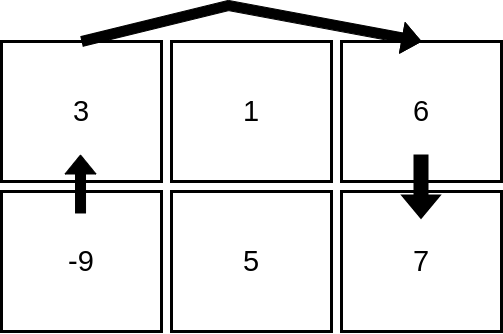
输入：mat = [[3,1,6],[-9,5,7]]
输出：4
解释：上图展示了从第 2 行、第 1 列的单元格开始，可以访问 4 个单元格。可以证明，无论从哪个单元格开始，最多只能访问 4 个单元格，因此答案是 4 。  

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• -105 <= mat[i][j] <= 105

动态规划 + 优化（如何思考？）

https://leetcode.cn/problems/maximum-strictly-increasing-cells-in-a-matrix/solution/dong-tai-gui-hua-you-hua-pythonjavacgo-b-axv0/

class Solution {/**直接DP超时定义 f[i][j] 表示到达 mat[i][j] 时所访问的单元格的最大数量。那么答案就是所有 f[i][j] 的最大值。考虑转移来源，不需要知道具体从哪个单元格转移过来，只需要知道转移来源的最大值时多少维护每一行的 f[i][j] 的最大值维护每一列的 f[i][j] 的最大值按照元素值的顺序从小到大计算*/public int maxIncreasingCells(int[][] mat) {var g = new TreeMap<Integer, List<int[]>>();int m = mat.length, n = mat[0].length;for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)// 相同元素放在同一组，统计位置g.computeIfAbsent(mat[i][j], k -> new ArrayList<>()).add(new int[]{i, j});int ans = 0;int[] rowMax = new int[m], colMax = new int[n];for (var pos : g.values()) { // 按照元素值从小到大进行遍历，顺序与矩阵每行每列的顺序无关var mx = new int[pos.size()];  // 先把最大值算出来，再更新 rowMax 和 colMaxfor (int i = 0; i < pos.size(); i++) {mx[i] = Math.max(rowMax[pos.get(i)[0]], colMax[pos.get(i)[1]]) + 1;ans = Math.max(ans, mx[i]);}for (int k = 0; k < pos.size(); k++) {int i = pos.get(k)[0], j = pos.get(k)[1];rowMax[i] = Math.max(rowMax[i], mx[k]); // 更新第 i 行的最大 f 值colMax[j] = Math.max(colMax[j], mx[k]); // 更新第 j 列的最大 f 值}}return ans;}
}