平衡树原理讲解
平衡树——Treap
文章目录
- 平衡树——Treap
- BST
- 定义
- 性质
- 操作
- 插入`insert(o, v)`
- 删除`del(o, v)`
- 找前驱 / 后继`get_prev(o)、get_next(o)`
- 查找最大 / 最小值`get_min(o)、get_max(o)`
- 求元素排名`get_rank(o)`
- 查找排名为 k k k的元素`get_value_by_rank`
- 平衡树
- 左旋、右旋`zag(o)、zig(o)`
- 左旋
- 右旋
BST
定义
-
空树是二叉搜索树。
-
若二叉搜索树的左子树不为空,则其左子树上所有点的附加权值均小于其根节点的值。
-
若二叉搜索树的右子树不为空,则其右子树上所有点的附加权值均大于其根节点的值。
-
二叉搜索树的左右子树均为二叉搜索树。
性质
二叉搜索树的中序遍历是一个有序序列
操作
插入insert(o, v)
-
若 o o o 为空,直接返回一个值为 v v v 的新节点。
-
若 o o o 的权值等于 v v v,该节点的附加域该值出现的次数自增 1 1 1。
-
若 o o o 的权值大于 v v v,在 o o o 的左子树中插入权值为 v v v 的节点。
-
若 o o o 的权值小于 v v v,在 o o o 的右子树中插入权值为 v v v 的节点。
删除del(o, v)
先在二叉搜索树中找到权值为 v 的节点,分类讨论如下:
-
若该节点的附加 cnt \textit{cnt} cnt 大于 1 1 1,只需要减少 cnt \textit{cnt} cnt。
-
若该节点的附加 cnt \textit{cnt} cnt 为 1 1 1:
-
若 o o o 为叶子节点,直接删除该节点即可。
-
若 o o o 为链节点,即只有一个儿子的节点,返回这个儿子。
-
若 o o o 有两个非空子节点,一般是用它左子树的最大值或右子树的最小值代替它,然后将它删除。
-
找前驱 / 后继get_prev(o)、get_next(o)
前(后)驱表示中序遍历中前(后)一个位置,以前驱为例
- 存在左子树,则找到左子树中最右边的元素,并返回。
- 不存在左子树,找第一个祖先节点中节点 o o o位于其右子树中,返回这个祖先节点
查找最大 / 最小值get_min(o)、get_max(o)
由二叉搜索树的性质可得,二叉搜索树上的最小值为二叉搜索树左链的顶点,最大值为二叉搜索树右链的顶点。
求元素排名get_rank(o)
排名定义为将数组元素排序后第一个相同元素之前的数的个数加一
查找一个元素的排名,首先从根节点跳到这个元素,若向右跳,答案加上左儿子节点个数加当前节点重复的数个数,最后答案加上终点的左儿子子树大小加一。
查找排名为 k k k的元素get_value_by_rank
在一棵子树中,根节点的排名取决于其左子树的大小。
若其左子树的大小大于等于 k k k,则该元素在左子树中;
若其左子树的大小在区间 [ k − cnt , k − 1 ] [k-\textit{cnt},k-1] [k−cnt,k−1]( cnt \textit{cnt} cnt 为当前结点的值的出现次数)中,则该元素为子树的根节点;
若其左子树的大小小于 k − cnt k-\textit{cnt} k−cnt,则该元素在右子树中。
平衡树
对于一般的二叉搜索树,有可能退化为链表。想象一棵每个结点只有右孩子的二叉搜索树,那么它的性质就和链表一样,插入与查找时间都是 O ( n ) O(n) O(n)
二叉搜索树的「平衡」概念是指:每一个结点的左子树和右子树高度差最多为 1。
可以对不满足平衡条件的二叉搜索树进行调整,使不平衡的二叉搜索树变得平衡。
调整要保证的标准还有二叉搜索树先天自带的条件:二叉搜索树,按照中序遍历,得到从小到大的结点值序列。对于任意一个结点,左子树各结点的最大值,小于该结点的值;该结点的值,小于右子树各结点的最小值。只有保证这一点才能称为一个二叉搜索树。
左旋、右旋zag(o)、zig(o)
左旋
左旋,左旋也称为「左单旋转」或「RR 平衡旋转」。对于结点 A A A 的左旋操作是指:将 A A A 的右孩子 B B B 向左上旋转,代替 A A A 成为根节点,将 A A A 结点向左下旋转成为 B B B 的左子树的根结点, B B B 的原来的左子树变为 A A A 的右子树。
右旋
右旋,右旋也称为「右单旋转」或「LL 平衡旋转」。对于结点 A A A 的右旋操作是指:将 A A A 的左孩子 B B B 向右上旋转,代替 A A A 成为根节点,将 A A A 结点向右下旋转成为 B B B 的右子树的根结点, B B B 的原来的右子树变为 A A A 的左子树。

相关文章:

平衡树原理讲解
平衡树——Treap 文章目录 平衡树——TreapBST定义性质操作插入insert(o, v)删除del(o, v)找前驱 / 后继get_prev(o)、get_next(o)查找最大 / 最小值get_min(o)、get_max(o)求元素排名get_rank(o)查找排名为 k k k的元素get_value_by_rank 平衡树左旋、右旋zag(o)、zig(o)左旋右…...
-第七节)
SpringMVC框架面试专题(初级-中级)-第七节
欢迎大家一起探讨~如果可以帮到大家请为我点赞关注哦~后续会持续更新 问题: 1.Spring MVC框架中的注解是什么?请举例说明如何使用注解。 解析: Spring MVC是一个基于MVC(Model-View-Controller…...

爬虫实战案例
预计更新 一、 爬虫技术概述 1.1 什么是爬虫技术 1.2 爬虫技术的应用领域 1.3 爬虫技术的工作原理 二、 网络协议和HTTP协议 2.1 网络协议概述 2.2 HTTP协议介绍 2.3 HTTP请求和响应 三、 Python基础 3.1 Python语言概述 3.2 Python的基本数据类型 3.3 Python的流程控制语句 …...

ConcurrentLinkedQueue非阻塞无界链表队列
ConcurrentLinkedQueue非阻塞无界链表队列 ConcurrentLinkedQueue是一个线程安全的队列,基于链表结构实现,是一个无界队列,理论上来说队列的长度可以无限扩大。 与其他队列相同,ConcurrentLinkedQueue 也采用的是先进先出&#…...

排序算法稳定性
稳定性: 用一句话总结排序算法的稳定性就是:同样的值,在排完序之后改不改变相对次序。 举例:arr[] {3,2,1,2,1,3},数组中共有1、2 、3各2个数,排完序之后arr1[] {1,1,2,2,3,3}。稳定性是指排完序之后&…...

统计学期末复习整理
统计学:描述统计学和推断统计学。计量尺度:定类尺度、定序尺度、定距尺度、定比尺度。 描述统计中的测度: 1.数据分布的集中趋势 2.数据分布的离散程度 3.数据分布的形状。 离散系数 也称为标准差系数,通常是用一组数据的标准差与…...

Sketch在线版免费使用,Windows也能用的Sketch!
Sketch 的最大缺点是它对 Windows/PC 用户不友好。它是一款 Mac 工具,无法在浏览器中运行。此外,使用 Sketch 需要安装其他插件才能获得更多响应式设计工具。然而,现在有了 Sketch 网页版工具即时设计替代即时设计! 即时设计几乎…...

详解uni-app项目运行在安卓真机调试
详解uni-app项目运行在安卓真机调试 uni-app项目运行在安卓真机调试 文章目录 详解uni-app项目运行在安卓真机调试前言为什么要用真机调试?真机调试操作步骤总结 前言 UNI-APP学习系列之详解uni-app项目运行在安卓真机调试 为什么要用真机调试? 因为安…...

体积小、无广告、超实用的5款小工具
大家好,我又来啦,今天给大家带来的5款软件,共同特点都是体积小、无广告、超实用,大家观看完可以自行搜索下载哦。 1.动态桌面——WinDynamicDesktop WinDynamicDesktop是一款用于根据时间和地点自动更换桌面壁纸的工具。它可以让…...

OZON好出单吗?新手如何做?注意事项是什么?
最近OZON的势头确实很猛,东哥后台也收到了很多关于OZON的咨询,很多想尝试跨境电商的新手卖家都对这个平台跃跃欲试,其中问最多的就是,“OZON好出单吗?”“新手做OZON需要注意什么?避开哪些坑?”…...
性能测试需求分析有哪些?怎么做?
目录 性能测试必要性评估 常见性能测试关键评估项如下: 性能测试工具选型 性能测试需求分析 性能测试需求评审 性能测试需求分析与传统的功能测试需求有所不同,功能测试需求分析重点在于从用户层面分析被测对象的功能性、易用性等质量特性ÿ…...

STM32F103RCT6 -- 基于FreeRTOS 的USART1 串口通讯
1. 在STM32F103RCT6 单片机上跑FreeRTOS 实时操作系统,使用串口USART1 通讯,发送 – 接收数据,实现上位机与下位机的通信 使用 FreeRTOS 提供的队列(Queue)机制来实现数据的接收和发送 2. USART1 配置: …...

区间预测 | MATLAB实现基于QRCNN-LSTM-Multihead-Attention多头注意力卷积长短期记忆神经网络多变量时间序列区间预测
区间预测 | MATLAB实现基于QRCNN-LSTM-Multihead-Attention多头注意力卷积长短期记忆神经网络多变量时间序列区间预测 目录 区间预测 | MATLAB实现基于QRCNN-LSTM-Multihead-Attention多头注意力卷积长短期记忆神经网络多变量时间序列区间预测效果一览基本介绍模型描述程序设计…...
)
递归--打印一个字符串的全部排列(java)
打印一个字符串的全部排列 打印一个字符串的全部排列解题思路打印一个字符串的全部排列,要求不要出现重复的排列递归专题 打印一个字符串的全部排列 自负串全排序: 举例: abc 的全排序是: abc acb bac bca cba cab 解题思路 因为每个字符都要选,其实就是选择每个字符…...

【001 设备驱动】主设备号和次设备号的用途
一、请简述主设备号和次设备号的用途 Linux 中每个设备都有一个设备号,设备号由主设备号和次设备号两部分组成,主设备号表示某一个具体的驱动,次设备号表示使用这个驱动的各个设备。 Linux 提供了一个名为 dev_t 的数据类型表示设备号&…...

移动端PDF在线预览
苹果手机可以直接在线预览PDF文件,而安卓手机不行,必须得下载(如图),所以需要解决一下 1.准备所需js文件 (1)js下载地址https://mozilla.github.io/pdf.js/ (2)下载步骤 ①:打开网址后&#x…...

虚拟机两次寻址
一次寻址: 虚拟、逻辑地址:CS(段选择子) eip(段内偏移)> 线性地址 : 32位或64位 通过页表> 物理地址 x86: 页面大小4k pte4个字节 10-10-12 (不管是x86 x86PAE x64下页内偏…...
DRF之JWT认证
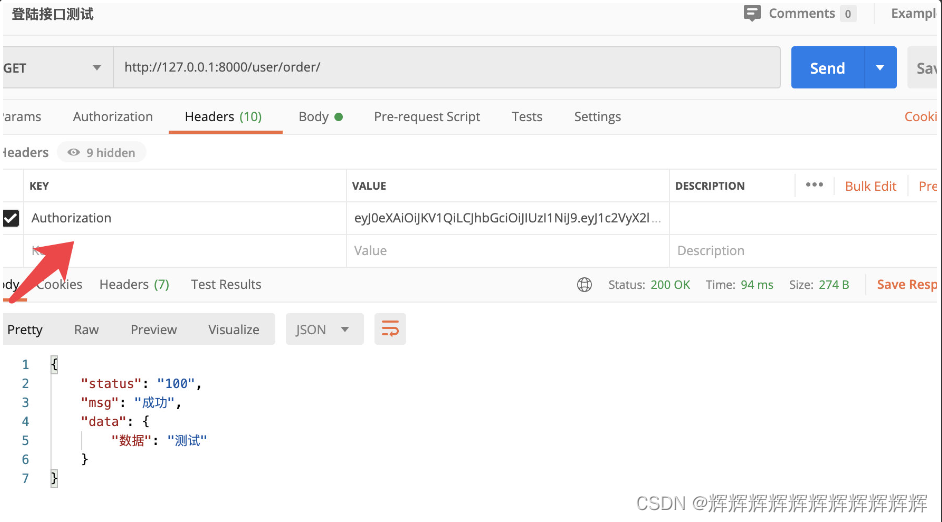
一、JWT认证 在用户注册或登录后,我们想记录用户的登录状态,或者为用户创建身份认证的凭证。我们不再使用Session认证机制,而使用Json Web Token(本质就是token)认证机制。 Json web token (JWT), 是为了在网络应用环…...

华为OD机试真题 Java 实现【放苹果】【2022Q4 100分】
一、题目描述 把m个同样的苹果放在n个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法? 注意:如果有7个苹果和3个盘子,(5,1,1)和(1,5,1)被视为是同一种分法。 数据范围:0≤m≤10 ,1≤n≤10 。 二、输入描述 输入两个int整数。 三、输出描述 输…...

拼多多继续ALL IN
2023年注定是中国电商不平凡的一年。 随着网购用户数量见顶,经济形势进入新常态,电商平台已经来到了短兵相接的肉搏战阶段。 此刻的618大促,硝烟弥漫,刀光剑影,电商“决战”似乎是迫在眉睫。对各个平台来说,…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...
