C#,码海拾贝(28)——求解“对称正定方程组”的“平方根法”之C#源代码
using System;
namespace Zhou.CSharp.Algorithm
{
/// <summary>
/// 求解线性方程组的类 LEquations
/// 原作 周长发
/// 改编 深度混淆
/// </summary>
public static partial class LEquations
{
/// <summary>
/// 求解对称正定方程组的平方根法
/// </summary>
/// <param name="mtxLECoef">指定的系数矩阵</param>
/// <param name="mtxLEConst">指定的常数矩阵</param>
/// <param name="mtxResult">Matrix引用对象,返回方程组解矩阵</param>
/// <return>bool 型,方程组求解是否成功</return>
public static bool GetRootsetCholesky(Matrix mtxLECoef, Matrix mtxLEConst, Matrix mtxResult)
{
int i, j, k, u, v;
// 方程组属性,将常数矩阵赋给解矩阵
Matrix mtxCoef = new Matrix(mtxLECoef);
mtxResult.SetValue(mtxLEConst);
int n = mtxCoef.GetNumColumns();
int m = mtxResult.GetNumColumns();
double[] pDataCoef = mtxCoef.GetData();
double[] pDataConst = mtxResult.GetData();
// 非对称正定系数矩阵,不能用本方法求解
if (pDataCoef[0] <= 0.0)
{
return false;
}
pDataCoef[0] = Math.Sqrt(pDataCoef[0]);
for (j = 1; j <= n - 1; j++)
{
pDataCoef[j] = pDataCoef[j] / pDataCoef[0];
}
for (i = 1; i <= n - 1; i++)
{
u = i * n + i;
for (j = 1; j <= i; j++)
{
v = (j - 1) * n + i;
pDataCoef[u] = pDataCoef[u] - pDataCoef[v] * pDataCoef[v];
}
if (pDataCoef[u] <= 0.0)
{
return false;
}
pDataCoef[u] = Math.Sqrt(pDataCoef[u]);
if (i != (n - 1))
{
for (j = i + 1; j <= n - 1; j++)
{
v = i * n + j;
for (k = 1; k <= i; k++)
{
pDataCoef[v] = pDataCoef[v] - pDataCoef[(k - 1) * n + i] * pDataCoef[(k - 1) * n + j];
}
pDataCoef[v] = pDataCoef[v] / pDataCoef[u];
}
}
}
for (j = 0; j <= m - 1; j++)
{
pDataConst[j] = pDataConst[j] / pDataCoef[0];
for (i = 1; i <= n - 1; i++)
{
u = i * n + i;
v = i * m + j;
for (k = 1; k <= i; k++)
{
pDataConst[v] = pDataConst[v] - pDataCoef[(k - 1) * n + i] * pDataConst[(k - 1) * m + j];
}
pDataConst[v] = pDataConst[v] / pDataCoef[u];
}
}
for (j = 0; j <= m - 1; j++)
{
u = (n - 1) * m + j;
pDataConst[u] = pDataConst[u] / pDataCoef[n * n - 1];
for (k = n - 1; k >= 1; k--)
{
u = (k - 1) * m + j;
for (i = k; i <= n - 1; i++)
{
v = (k - 1) * n + i;
pDataConst[u] = pDataConst[u] - pDataCoef[v] * pDataConst[i * m + j];
}
v = (k - 1) * n + k - 1;
pDataConst[u] = pDataConst[u] / pDataCoef[v];
}
}
return true;
}
}
}
相关文章:
C#,码海拾贝(28)——求解“对称正定方程组”的“平方根法”之C#源代码
using System; namespace Zhou.CSharp.Algorithm { /// <summary> /// 求解线性方程组的类 LEquations /// 原作 周长发 /// 改编 深度混淆 /// </summary> public static partial class LEquations { /// <summary> /…...

碳纤维单丝外径测试中的纳米分辨率激光衍射法解决方案
摘要:碳纤维单丝热膨胀系数是碳纤维复合材料设计、生产与可靠性和寿命评估的重要参数,本文针对单丝径向高温热膨胀系数测试这一难题提出了相应的解决方案。解决方案的核心内容是基于激光衍射法和高温辐射加热,并采用衍射轮廓拟合技术以及相应…...

服务(第三十二篇)nginx做缓存服务器
nginx作为缓存服务配置语法 1、proxy_cache_path 配置语法(即缓存路径配置语法) Syntax:proxy_cache_path path [levelslevels] [use_temp_pathon|off] keys_zonename:size [inactivetime] [max_sizesize] [manager_filesnumber] [manager_s…...
Java 集合、数组、字符串的相互转换(关于list.toArray(new String[0])的源码分析)
在 Java 中,可以通过以下方式实现集合、数组和字符串之间的相互转换。 一、集合和数组的相互转化 ①、将集合转为数组:(toArray 方法) List<String> list new ArrayList<>(); list.add("apple"); lis…...
Redis的全局命令及相关误区
Redis中所说的数据结构是针对key-value中的value而言的。主要的结构包括String、哈希表、列表、集合等等在redis中存在16个库,涉及到后期的集群搭建只能使用0号库最为方便 查看所有键(支持通配符) keys * keys S*返回当前数据库中的键总数 …...

C++核心编程—类和对象,类的三大特性——封装、继承、多态
纵有疾风起,人生不言弃。本文篇幅较长,如有错误请不吝赐教,感谢支持。 💬文章目录 一.类和对象的概念①什么是对象?②抽象和类1.类的基本概念2.类的声明与定义:3.对象的创建与使用 二.类的封装①为什么有封…...

keep-alive 是 Vue 内置的一个组件,被用来缓存组件实例。
文章目录 简介注意点使用 keep-alive 有以下优缺点优点缺点 简介 keep-alive 是 Vue 内置的一个组件,被用来缓存组件实例。 使用 keep-alive 包裹动态组件时,被包裹的组件实例将会被缓存起来,而不会被销毁,直到 keep-alive 组件…...

(八)Spring之IOC控制反转、DI依赖注入介绍和使用(详解)
文章目录 前言SpringSpring IOC 简介BeanIOC 概述IOC 本质理解 Spring IOC 应用IOC xml装配IOC 依赖注入IOC Bean的作用域 IoC 自动装配Bean 的自动装配注解实现自动装配 IoC 使用注解开发模拟实现Spring IoC 前言 “Spring”在不同的上下文中表示不同的事物。它可以用来引用 …...
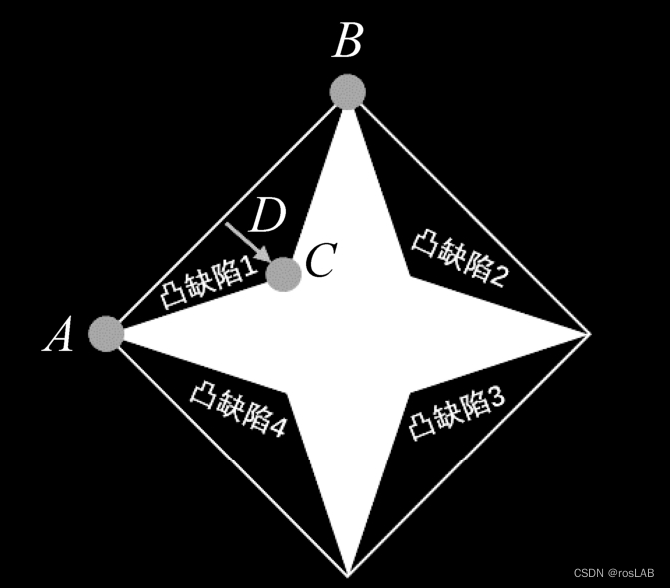
凸缺陷 convexityDefects
获取凸包,可以参考我的这篇文章: 凸包(Convex Hull)代码实现案例 获取了凸包之后,可以干什么呢? 凸缺陷凸包与轮廓之间的部分称为凸缺陷。凸缺陷可用来处理手势识别等问题。 通常情况下,使用如…...

c语言编程练习题:7-43 Shuffling Machine
Shuffling is a procedure used to randomize a deck of playing cards. Because standard shuffling techniques are seen as weak, and in order to avoid “inside jobs” where employees collaborate with gamblers by performing inadequate shuffles, many casinos empl…...

ffmpeg enum AVChannel枚举解析
AVChannel枚举是在2022-12-20的提交中添加的,对应的版本号是5.1. 这个提交的描述是"avutil/channel_layout: add AVChannel enum and related functions"。 原型 typedef struct AVChannelCustom {enum AVChannel id;char name[16];void *opaque; } AVCh…...

invest模型教程
详情点击链接:invest模型教程——建议收藏 1.生态系统服务 2.InVEST模型 3.InVEST所需数据(分辨率、格式、投影系统等)、获取及标准化预处理 4.InVEST运行 5.ArcGIS工具支撑InVEST模型 5.1ArcGIS数据形式与数据格式、数据格式之间的相互转换…...
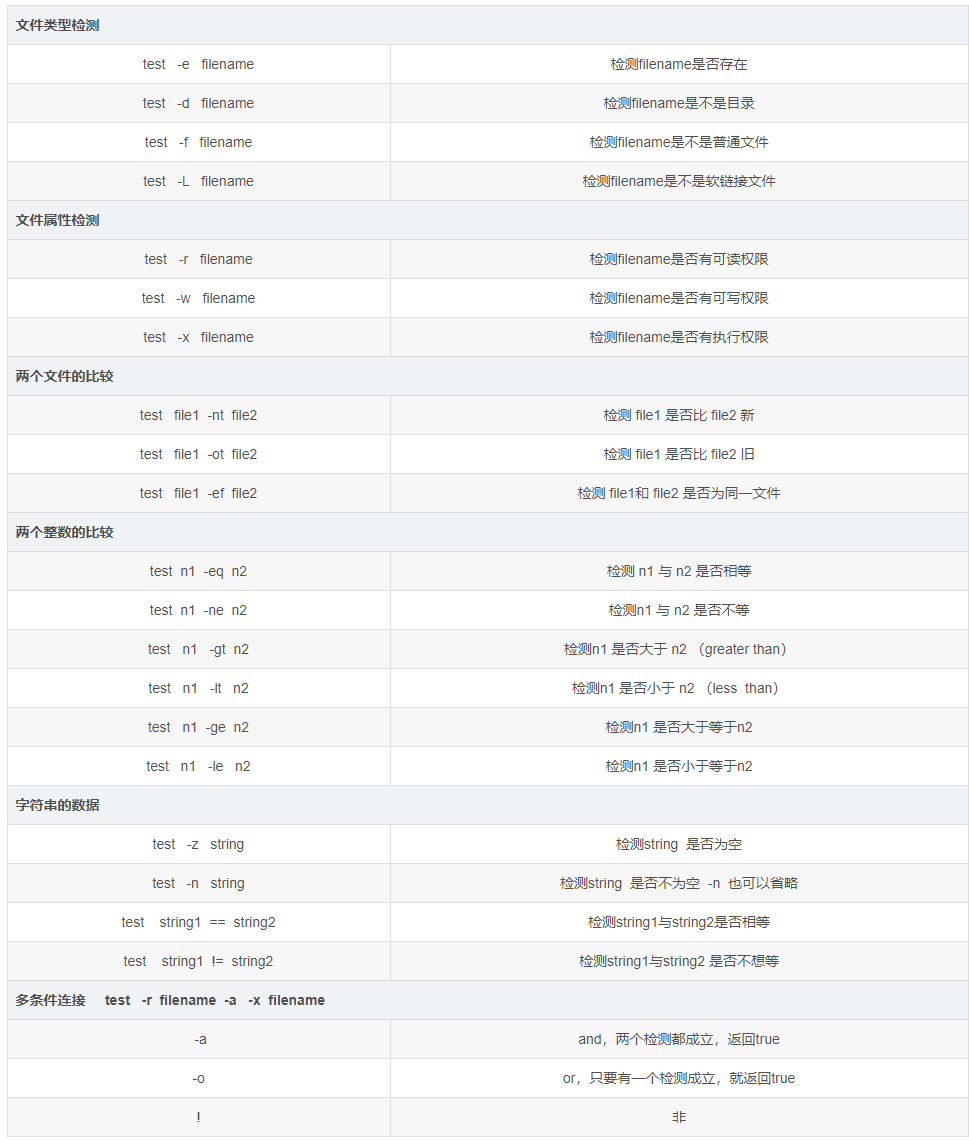
LinuxShell编程
Shell编程 Shell的概念介绍 命令解释器 Shell是命令解释器(command interpreter),是Unix操作系统的用户接口,程序从用户接口得到输入信息,shell将用户程序及其输入翻译成操作系统内核(kernel)能够识别的指令&#x…...
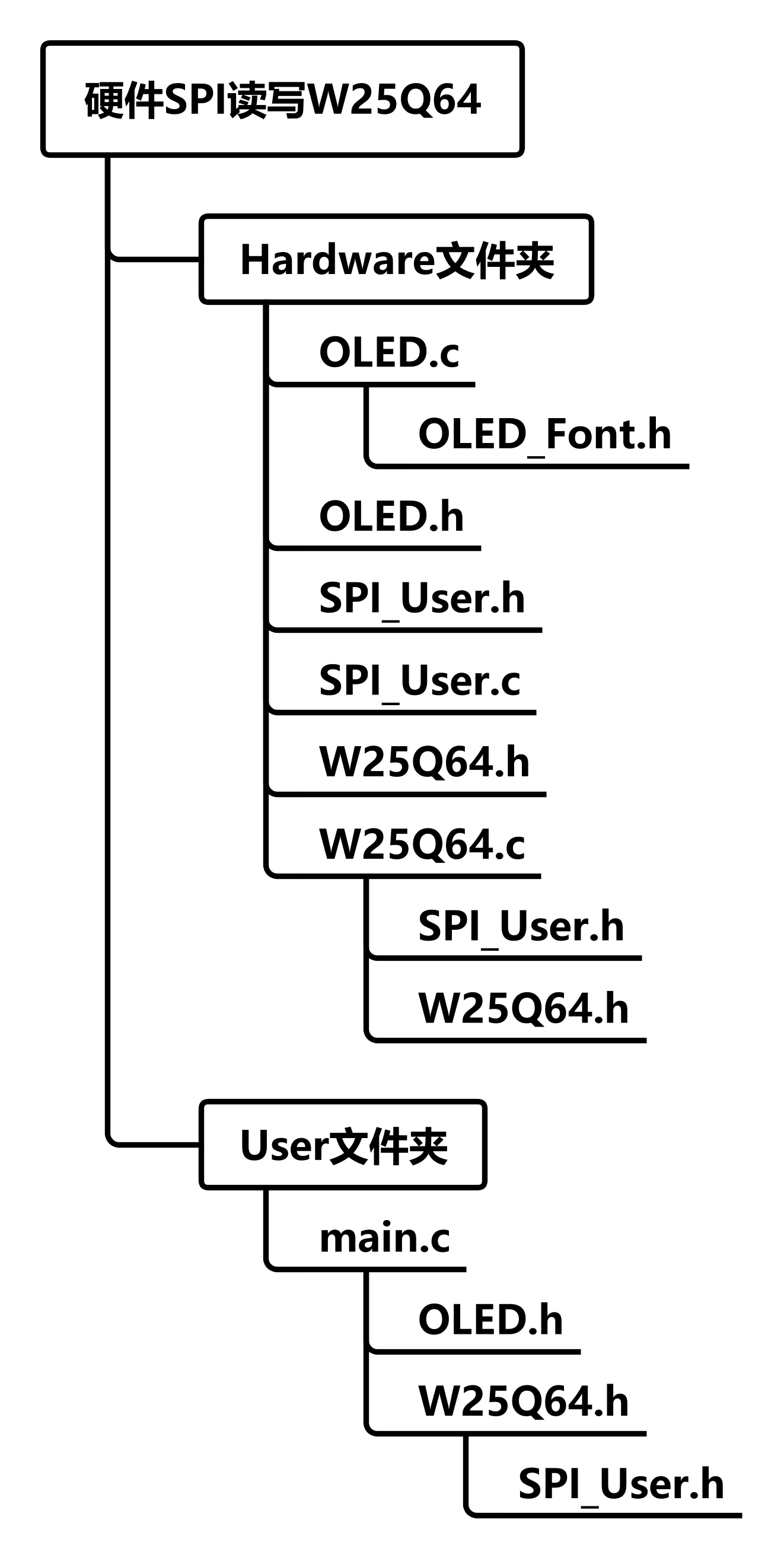
stm32学习笔记-11 SPI通信
11 SPI通信 文章目录 11 SPI通信11.1 SPI通信协议11.2 W25Q64简介11.3 实验:软件SPI读写W25Q6411.4 SPI通信外设11.5 实验:硬件SPI读写W25Q64 注:笔记主要参考B站 江科大自化协 教学视频“ STM32入门教程-2023持续更新中”。 注:…...
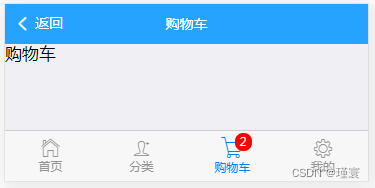
“微商城”项目(3页面布局)
1.设置标题 设置页面头部标题,方便告诉用户当前显示的是哪一个页面。编辑src\router.js文件,示例代码如下。 routes: [{ path: /, redirect: /home, meta: { title: 首页 } },{ path: /home, component: Home, name: home, meta: { title: 首页 } } ] …...

Java 八股文 - MySQL
MySQL 1. MySQL 有几种锁? 三种锁的特点 表级锁:开销小,加锁快;不会出现死锁;锁定颗粒度大,发生锁冲突的概率最高,并发度最低。行级锁:开销大,加锁慢;会…...
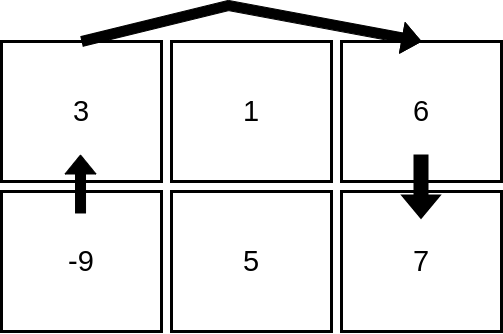
周赛347(模拟、思维题、动态规划+优化)
文章目录 周赛347[2710. 移除字符串中的尾随零](https://leetcode.cn/problems/remove-trailing-zeros-from-a-string/)模拟 [2711. 对角线上不同值的数量差](https://leetcode.cn/problems/difference-of-number-of-distinct-values-on-diagonals/)模拟 [2712. 使所有字符相等…...

String AOP的使用
面向切面编程,面向特定方法编程,以方法为对象,在不修改原方法的基础上,对方法进行操作扩展等,底层是通过动态代理实现的 使用开发步骤: 1、创建一个类,加上Aspect声明为一个AOP切面类ÿ…...
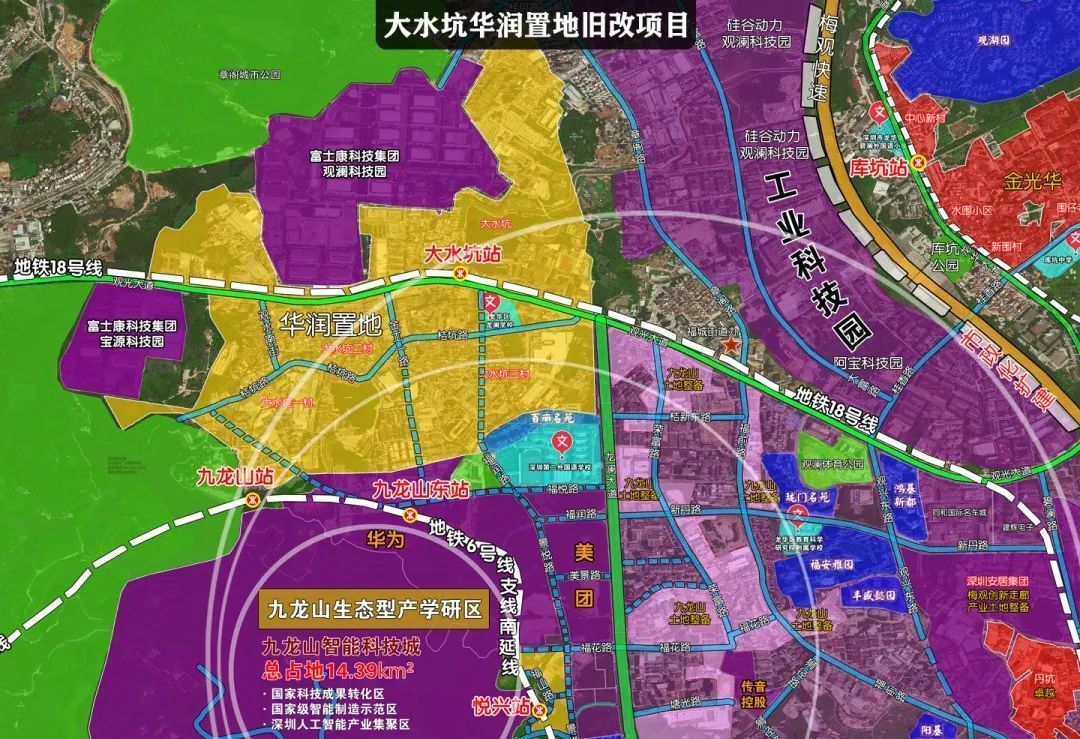
华为芯片基地旁,龙华科技小镇大水坑片区城市更新单元旧改项目
项目位置:龙华观澜大水坑社区,位于梅观创新走廊九龙山产学研片区内 占地面积:总面积198万平方米,其中项目第一期60万平米开 发 商: 华润集团申报主体:华润置地项目:龙华科技小镇大水坑片区城市…...

论文阅读 | 频谱监测、认知电子战、网电攻击
文章目录 1.《超短波信号的频谱监测与信号源定位》1.1 信号预处理技术1.2 对指定频段的宽带信号截获、分析以及频率分选研究1.3 对指定频段的信号进行最佳分频段扫描分析并还原原信号1.4 总结2.《认知电子战理论及关键技术研究》2.1 认知电子战发展现状2.2 认知电子战发展趋势分…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
