My Note of Diffusion Models
Diffusion Models
Links: https://theaisummer.com/diffusion-models/
Markovian Hierachical VAE
rvs:
- data: x 0 x_{0} x0,
- representation: x T x_{T} xT
( p ( x 0 , x 1 , ⋯ , x T ) , q ( x 1 , ⋯ , x T ∣ x 0 ) ) (p(x_0,x_1,\cdots,x_T),q(x_1,\cdots,x_{T}|x_0)) (p(x0,x1,⋯,xT),q(x1,⋯,xT∣x0))
where x 1 , ⋯ , x T x_1,\cdots,x_T x1,⋯,xT is unobservable, and
- generative model/backward trajectory:
p ( x 0 , x 1 , ⋯ , x T ) = p ( x T ) ∏ t p ( x t − 1 ∣ x t ) p(x_0,x_1,\cdots,x_T)=p(x_T)\prod_tp(x_{t-1}|x_{t}) p(x0,x1,⋯,xT)=p(xT)t∏p(xt−1∣xt) - forward trajectory(Markov process):
q ( x 1 , ⋯ , x T ∣ x 0 ) ) = ∏ t q ( x t ∣ x t − 1 ) q(x_1,\cdots,x_{T}|x_0))=\prod_tq(x_{t}|x_{t-1}) q(x1,⋯,xT∣x0))=t∏q(xt∣xt−1)
E L B O : = ∫ q ( x T ∣ x 0 ) log p ( x T ) q ( x T ∣ x 0 ) d x T + ∑ t = 2 T ∫ q ( x t − 1 , x t ∣ x 0 ) log p ( x t − 1 ∣ x t ) q ( x t − 1 ∣ x t , x 0 ) d x t − 1 x t + ∫ q ( x 1 ∣ x 0 ) log p ( x 1 ∣ x 0 ) d x 1 ELBO:=\int q(x_{T}|x_{0}) \log \frac{p(x_{T})}{q(x_{T}|x_{0})}\mathrm{d}x_{T}\\ +\sum_{t=2}^T \int q(x_{t-1},x_{t}|x_{0})\log \frac{p(x_{t-1}|x_{t})}{q(x_{t-1}|x_{t}, x_{0})}\mathrm{d}x_{t-1}x_{t}\\+\int q(x_{1}|x_{0})\log p(x_{1}|x_{0})\mathrm{d}x_{1} ELBO:=∫q(xT∣x0)logq(xT∣x0)p(xT)dxT+t=2∑T∫q(xt−1,xt∣x0)logq(xt−1∣xt,x0)p(xt−1∣xt)dxt−1xt+∫q(x1∣x0)logp(x1∣x0)dx1
Loss
L o s s : = − E L B O = D K L ( q ( x T ∣ x 0 ) ∥ p ( x T ) ) + ∑ t = 2 T ∫ q ( x t ∣ x 0 ) d x t D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p ( x t − 1 ∣ x t ) ) − ∫ q ( x 1 ∣ x 0 ) log p ( x 1 ∣ x 0 ) d x 1 Loss:=-ELBO= D_{KL} (q(x_{T}|x_{0})\| p(x_{T}))\\ +\sum_{t=2}^T \int q(x_{t}|x_{0})\mathrm{d}x_{t}D_{KL}(q(x_{t-1}|x_{t}, x_{0})\|p(x_{t-1}|x_{t}))\\-\int q(x_{1}|x_{0})\log p(x_{1}|x_{0})\mathrm{d}x_{1} Loss:=−ELBO=DKL(q(xT∣x0)∥p(xT))+t=2∑T∫q(xt∣x0)dxtDKL(q(xt−1∣xt,x0)∥p(xt−1∣xt))−∫q(x1∣x0)logp(x1∣x0)dx1
- prior matching term
- denoising matching term
- reconstruction term
Diffusion Models
basic assumption
- tractable distr: p ( x T ) p(x_{T}) p(xT)
- forward trajectory(Markov process): q ( x t ∣ x t − 1 ) q(x_{t}|x_{t-1}) q(xt∣xt−1) is fixed (has no unlearned parameter)
Definition(Diffusion Model)
- tractable distr: p ( x T ) ∼ N ( 0 , 1 ) p(x_{T})\sim N(0,1) p(xT)∼N(0,1)
- generative model/backward trajectory: p ( x t − 1 ∣ x t ) ∼ N ( μ ( t ) , Σ ( t ) ) p(x_{t-1}|x_{t})\sim N(\mu(t),\Sigma(t)) p(xt−1∣xt)∼N(μ(t),Σ(t))
- forward trajectory(Gaussian diffusion): q ( x t ∣ x t − 1 ) ∼ N ( x t − 1 1 − β t , β t ) q(x_{t}|x_{t-1})\sim N(x_{t-1}\sqrt{1-\beta_t},\beta_t) q(xt∣xt−1)∼N(xt−11−βt,βt),
Parameters:
- β t = 1 − α t \beta_t=1-\alpha_t βt=1−αt or α ˉ t : = ∏ t α t \bar{\alpha}_t:=\prod_t\alpha_t αˉt:=∏tαt: noise schedule, where α t \alpha_t αt is small
- α ˉ t \sqrt{\bar{\alpha}_t} αˉt: signal rate

Fact.
- q ( x t ∣ x 0 ) ∼ N ( x 0 α ˉ t , 1 − α ˉ t ) q(x_{t}|x_{0})\sim N(x_{0}\sqrt{\bar{\alpha}_t},1-\bar{\alpha}_t) q(xt∣x0)∼N(x0αˉt,1−αˉt)
- q ( x t − 1 ∣ x t , x 0 ) ∼ N ( μ q ( x t , x 0 ) , σ 2 ( t ) ) q(x_{t-1}|x_{t},x_{0})\sim N(\mu_q(x_t ,x_0),\sigma^2(t)) q(xt−1∣xt,x0)∼N(μq(xt,x0),σ2(t)) where
μ q ( x t , x 0 ) : = α t ( 1 − α ˉ t − 1 ) x t − α ˉ t − 1 ( 1 − α t ) x 0 1 − α ˉ t = 1 α t x t − β t 1 − α ˉ t α t ϵ 0 \mu_q(x_t,x_0):=\frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_t-\sqrt{\bar\alpha_{t-1}}(1-\alpha_{t})x_0}{1-\bar\alpha_t}\\ =\frac{1}{\sqrt{\alpha_t}}x_t-\frac{\beta_t}{\sqrt{1-\bar\alpha_t}\sqrt{\alpha_t}}\epsilon_0 μq(xt,x0):=1−αˉtαt(1−αˉt−1)xt−αˉt−1(1−αt)x0=αt1xt−1−αˉtαtβtϵ0
and σ 2 ( t ) : = 1 − α ˉ t − 1 1 − α ˉ t β t \sigma^2(t):=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_{t} σ2(t):=1−αˉt1−αˉt−1βt.
Design I: p ( x t − 1 ∣ x t ) ∼ N ( μ ( t ) , Σ ( t ) ) p(x_{t-1}|x_{t})\sim N(\mu(t),\Sigma(t)) p(xt−1∣xt)∼N(μ(t),Σ(t)):
μ ( t ) = α t ( 1 − α ˉ t − 1 ) x t − β t α ˉ t − 1 x ^ ( x t , t ) 1 − α ˉ t Σ ( t ) = σ 2 ( t ) \mu(t)=\frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_t-\beta_{t}\sqrt{\bar\alpha_{t-1}}\hat{x}(x_t,t)}{1-\bar\alpha_t}\\ \Sigma(t)=\sigma^2(t) μ(t)=1−αˉtαt(1−αˉt−1)xt−βtαˉt−1x^(xt,t)Σ(t)=σ2(t)
Design II: p ( x t − 1 ∣ x t ) ∼ N ( μ ( t ) , Σ ( t ) ) p(x_{t-1}|x_{t})\sim N(\mu(t),\Sigma(t)) p(xt−1∣xt)∼N(μ(t),Σ(t)):
μ ( t ) = 1 α t x t − β t 1 − α ˉ t α t ϵ ^ ( x t , t ) Σ ( t ) = σ 2 ( t ) \mu(t)=\frac{1}{\sqrt{\alpha_t}}x_t-\frac{\beta_t}{\sqrt{1-\bar\alpha_t}\sqrt{\alpha_t}}\hat{\epsilon}(x_t,t)\\ \Sigma(t)=\sigma^2(t) μ(t)=αt1xt−1−αˉtαtβtϵ^(xt,t)Σ(t)=σ2(t)
Fact.
Under the design I:
D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) = 1 2 σ t 2 ( 1 − α ˉ t − 1 ) β t 2 ( 1 − α ˉ t ) 2 ∥ x ^ ( x t , t ) − x 0 ∥ 2 = 1 2 ( 1 1 − α ˉ t − 1 − 1 1 − α ˉ t ) ∥ x ^ ( x t , t ) − x 0 ∥ 2 D_{KL} (q(x_{t−1}|x_t , x_0) \| p_θ (x_{t−1} |x_t))=\frac{1}{2\sigma_t^2}\frac{(1-\bar{\alpha}_{t-1})\beta_t^2}{(1-\bar{\alpha}_{t})^2}\|\hat{x}(x_t,t)-x_0\|^2\\ =\frac{1}{2}(\frac{1}{1-\bar{\alpha}_{t-1}}-\frac{1}{1-\bar{\alpha}_{t}})\|\hat{x}(x_t,t)-x_0\|^2 DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))=2σt21(1−αˉt)2(1−αˉt−1)βt2∥x^(xt,t)−x0∥2=21(1−αˉt−11−1−αˉt1)∥x^(xt,t)−x0∥2
Under the design II:
D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) = 1 2 σ t 2 β t 2 ( 1 − α ˉ t ) α t 2 ∥ ϵ ^ ( x t , t ) − ϵ 0 ∥ 2 D_{KL} (q(x_{t−1}|x_t , x_0) \| p_θ (x_{t−1} |x_t))=\frac{1}{2\sigma_t^2}\frac{\beta_t^2}{(1-\bar{\alpha}_{t})\alpha_t^2}\|\hat{\epsilon}(x_t,t)-\epsilon_0\|^2 DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))=2σt21(1−αˉt)αt2βt2∥ϵ^(xt,t)−ϵ0∥2
Algorithm
Loss:
L = ∑ t L t L t ≈ ∑ ϵ ∼ N ( 0 , 1 ) ∥ ϵ − ϵ ^ ( x t , t ) ∥ 2 , ( 0 ≤ t < T ) L=\sum_t L_t\\ L_t\approx \sum_{\epsilon\sim N(0,1)}\|\epsilon-\hat{\epsilon}(x_{t},t)\|^2,(0\leq t<T) L=t∑LtLt≈ϵ∼N(0,1)∑∥ϵ−ϵ^(xt,t)∥2,(0≤t<T)
where x t : = α ˉ t x 0 + 1 − α ˉ t ϵ x_{t}:=\sqrt{\bar{\alpha}_t} x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon xt:=αˉtx0+1−αˉtϵ.
train NN ϵ ^ \hat\epsilon ϵ^ by data { ( ϵ ^ ( x t ( x 0 , i , ϵ i l ) , t ) , ϵ i l ) , ϵ i l ∼ N ( 0 , 1 ) , l = 1 , ⋯ , L } \{(\hat{\epsilon}(x_{t}(x_{0,i},\epsilon_{il}),t),\epsilon_{il}),\epsilon_{il}\sim N(0,1),l=1,\cdots, L\} {(ϵ^(xt(x0,i,ϵil),t),ϵil),ϵil∼N(0,1),l=1,⋯,L} with size of N L NL NL for each t t t。
Exercise
- Given a latent variable model p ( x , z ) p(x,z) p(x,z) with variational distr. q ( z ∣ x ) q(z|x) q(z∣x). q ( x ) q(x) q(x) represents data distr. and let q ( x , z ) = q ( z ∣ x ) q ( x ) q(x,z)=q(z|x)q(x) q(x,z)=q(z∣x)q(x).
∫ q ( x ) L x = ∫ q ( x , z ) log p ( x , z ) q ( z ∣ x ) ∼ D K L ( q ( x , z ) ∥ p ( x , z ) ) \int q(x)L_x=\int q(x,z)\log\frac{p(x,z)}{q(z|x)}\sim D_{KL}(q(x,z)\|p(x,z)) ∫q(x)Lx=∫q(x,z)logq(z∣x)p(x,z)∼DKL(q(x,z)∥p(x,z))
where L x L_x Lx is LEBO.
References
- Jonathan Ho, Ajay Jain, Pieter Abbeel. Denoising Diffusion Probabilistic Models, 2020.
- Calvin Luo, Understanding Diffusion Models: A Unified Perspective, 2022
相关文章:

My Note of Diffusion Models
Diffusion Models Links: https://theaisummer.com/diffusion-models/ Markovian Hierachical VAE rvs: data: x 0 x_{0} x0,representation: x T x_{T} xT ( p ( x 0 , x 1 , ⋯ , x T ) , q ( x 1 , ⋯ , x T ∣ x 0 ) ) (p(x_0,x_1,\cdots,x_T),q(x_1,\cdots,x_{T…...

【P37】JMeter 仅一次控制器(Once Only Controller)
文章目录 一、仅一次控制器(Once Only Controller)参数说明二、测试计划设计2.1、测试计划一2.1、测试计划二 一、仅一次控制器(Once Only Controller)参数说明 可以让控制器内部的逻辑只执行一次;单次的范围是针对某…...

cleanmymac要不要下载装机?好不好用
当我们收到一台崭新的mac电脑,第一步肯定是找到一款帮助我们管理电脑运行的“电脑管家”,监控内存运行、智能清理系统垃圾、清理Mac大文件旧文件、消除恶意软件、快速卸载更新软件、隐私保护、监控系统运行状况等。基本在上mac电脑防护一款CleanMyMac就够…...
:常见的DNS威胁与防御(中科三方))
DNS风险分析及防护研究(五):常见的DNS威胁与防御(中科三方)
DNS是互联网运行重要的基础设施,在全球互联网运转中扮演重要作用。互联网中的每一次访问都开始于一次DNS查询,从而将人们更好辨识的域名转换为数字化的IP地址。随着互联网的快速发展以及网络技术的快速发展,DNS固有的缺陷逐步暴露出来&#x…...

使用geoserver发布shp和tiff数据
一、安装并启动geoserver服务 1.1 下载geoserver 进入官网下载 由于geoserver是使用Java语言开发的,所以运行需要java的环境,不同geoserver的版本号对java的版本要求不同,所以选择版本时需注意对应java的版本要求,由于我本地安…...

谷歌周彦祺:LLM浪潮中的女性科学家多面手丨智源大会嘉宾风采
导读 大模型研发竞赛如火如荼,谷歌紧随OpenAI其后推出PalM2、Gemini等系列模型。Scaling Law是否仍然适用于当下的大模型发展?科技巨头与初创企业在竞争中各有哪些优势和劣势?模型研究者应秉持哪些社会责任? 2023智源大会「基础模…...
Burp模块
Target模块 记录流量 1.Target按主机或域名分类记录 2.HTTP History 按时间顺序记录且会记录很多次 3.Target模块的作用 (1)把握网站的整体情况 (2)对一次工作的域进行分析 (3)分析网站存在的攻击面 …...
)
sql笔记:SQL SERVER字符串填充(标量值函数创建、标量值函数调用)
/*字符串填充 ,如果返回 -1 说明输入参数有错误*/ CREATE FUNCTION [dbo].[uf_pad_string] ( @string_unpadded VARCHAR(100), --123填充前字符串 @pad_char VARCHAR(1), --0 填充的字符串 @pad_count tinyint, --10 填充后字符串长度 @pad_p…...

python使用hTTP方法
Python中可以使用requests库来发送HTTP请求,其中包括GET、POST、PUT、DELETE等方法。下面是一个使用requests库发送HTTP请求的示例: python import requests # 发送GET请求 response requests.get(Example Domain) # 发送POST请求 data {key1: valu…...

JavaSE常用API
1. Math.round(11.5)等于多少?Math.round(- 11.5) 又等于多少? Math.round(11.5)的返回值是 12,Math.round(-11.5)的返回值是-11。四舍五入的原理是在参数上加 0.5然后进行取整。 2. switch 是否能作用在 byte 上,是否能作用在 long 上…...

华为OD机试之模拟商场优惠打折(Java源码)
模拟商场优惠打折 题目描述 模拟商场优惠打折,有三种优惠券可以用,满减券、打折券和无门槛券。 满减券:满100减10,满200减20,满300减30,满400减40,以此类推不限制使用; 打折券&…...

5月VR大数据:Quest 2下跌超1%,其它变化不大
Hello大家好,每月一期的VR内容/硬件大数据统计又和大家见面了。 想了解VR软硬件行情么?关注这里就对了。我们会统计Steam平台的用户及内容等数据,每月初准时为你推送,不要错过喔! 本数据报告包含:Steam VR硬…...
CW32系列模数转换器(ADC)
模数转换器(ADC)的主要功能是将模拟量转换为数字量,方便MCU进行处理。下面以CW32L083为例介绍CW系列的模数转换器的特点和功能,并提供演示实例。 一、概述 CW32L083 内部集成一个 12 位精度、最高 1M SPS 转换速度的逐次逼近型模…...
电动力学专题:电磁场规范不变性与规范自由度
对称性,不变性,相对性,协变形 在现代物理学中常常被认为具有相同的含义(好拗口) 规范与规范的自由度 保证电磁场物理量不改变的情况下,有多组势可供选择,而每组势可以称为一个规范 规范不变性…...

max delay的应用场景与常见问题
max delay与min delay用来约束start points到endpoints点对点的路径长度,set_max_delay约束最大值,set_min_delay约束最小值。 max delay的-from和-to并不局限在get_pins,get_cells和get_clocks同样可以。 set_max_delay 5 -from UFF0/Q -to UFF1/D set_max_delay -from …...

非阻塞队列
非阻塞队列 首先我们要简单的理解下什么是非阻塞队列: 与阻塞队列相反,非阻塞队列的执行并不会被阻塞,无论是消费者的出队,还是生产者的入队。 在底层,非阻塞队列使用的是CAS(compare and swap)来实现线程执行的非阻塞…...
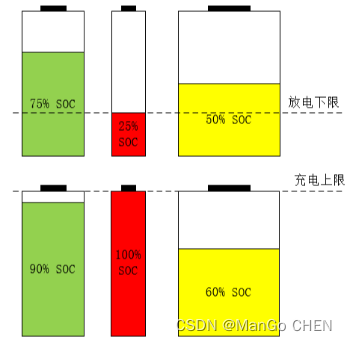
动力电池管理系统(BMS)
BMS技术 目录 BMS技术 一、BMS简介 二、BMS主要功能 1、参数检测 2、剩余电量(SOC)估计 3、充放电控制 4、热管理 5、均衡控制 6、故障诊断 7、信息监控 8、参数标定 9、CAN总线接口 三、BMS架构组成 1、BMS的拓扑架构 1、1集中式架构的B…...
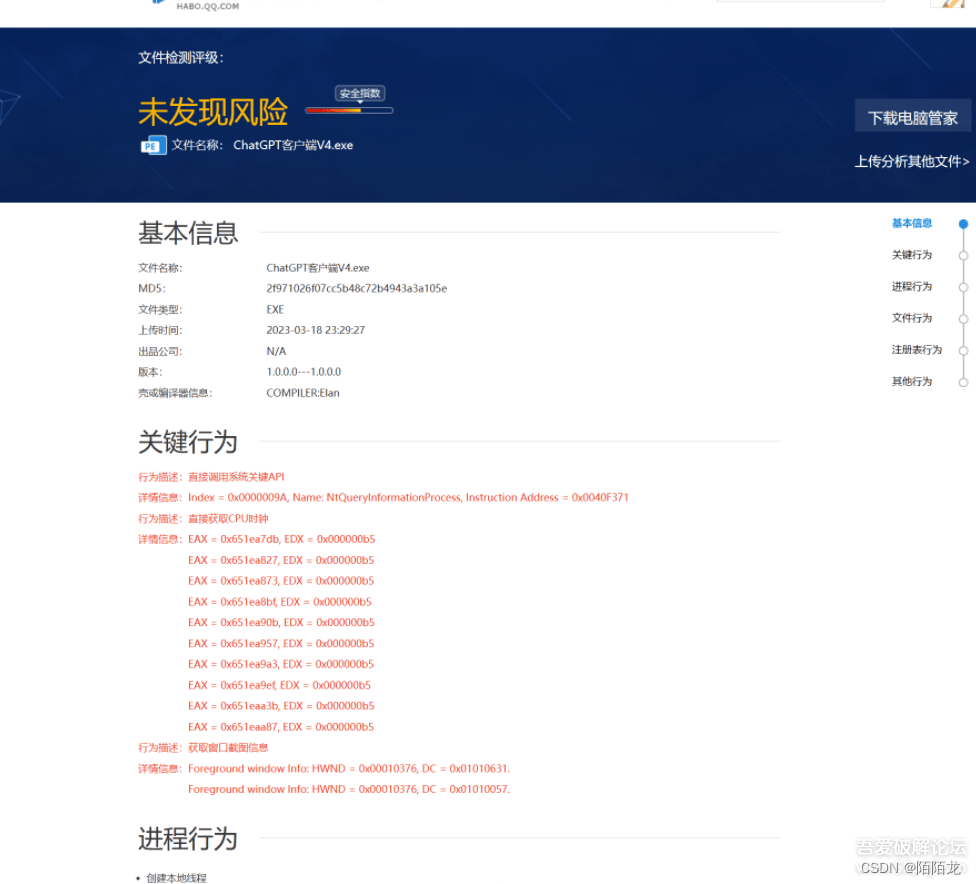
ChatGPT桌面客户端支持gpt4模型,附使用说明
#软件核心功能: 1、支持OpenAI官方秘钥及API2D双秘钥使用;如果全局魔法,可以自己用官方秘钥;没魔法国内可直接使用API2D秘钥; 2、内置GPT4模型选项,如果你的官方秘钥支持可直接使用;你也可以注册…...

Vivado下时序逻辑模块的仿真
文章目录 D触发器两级D触发器带异步复位的D触发器带异步复位和同步置数的D触发器移位寄存器单口RAM伪双口RAM真双口RAM单口ROM 组合逻辑电路在逻辑功能上特点是任意时刻的输出仅仅取决于当前时刻的输入,与电路原来的状态无关。 时序逻辑在逻辑功能上的特点是任意时刻…...

ThreadLocal的使用方式
1. ThreadLocal的使用方式 (1) 在关联数据类中创建private static ThreadLocal 在下面的类中,私有静态 ThreadLocal 实例(serialNum)为调用该类的静态 SerialNum.get() 方法的每个 线程维护了一个“序列号”,该方法将返回当前…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...
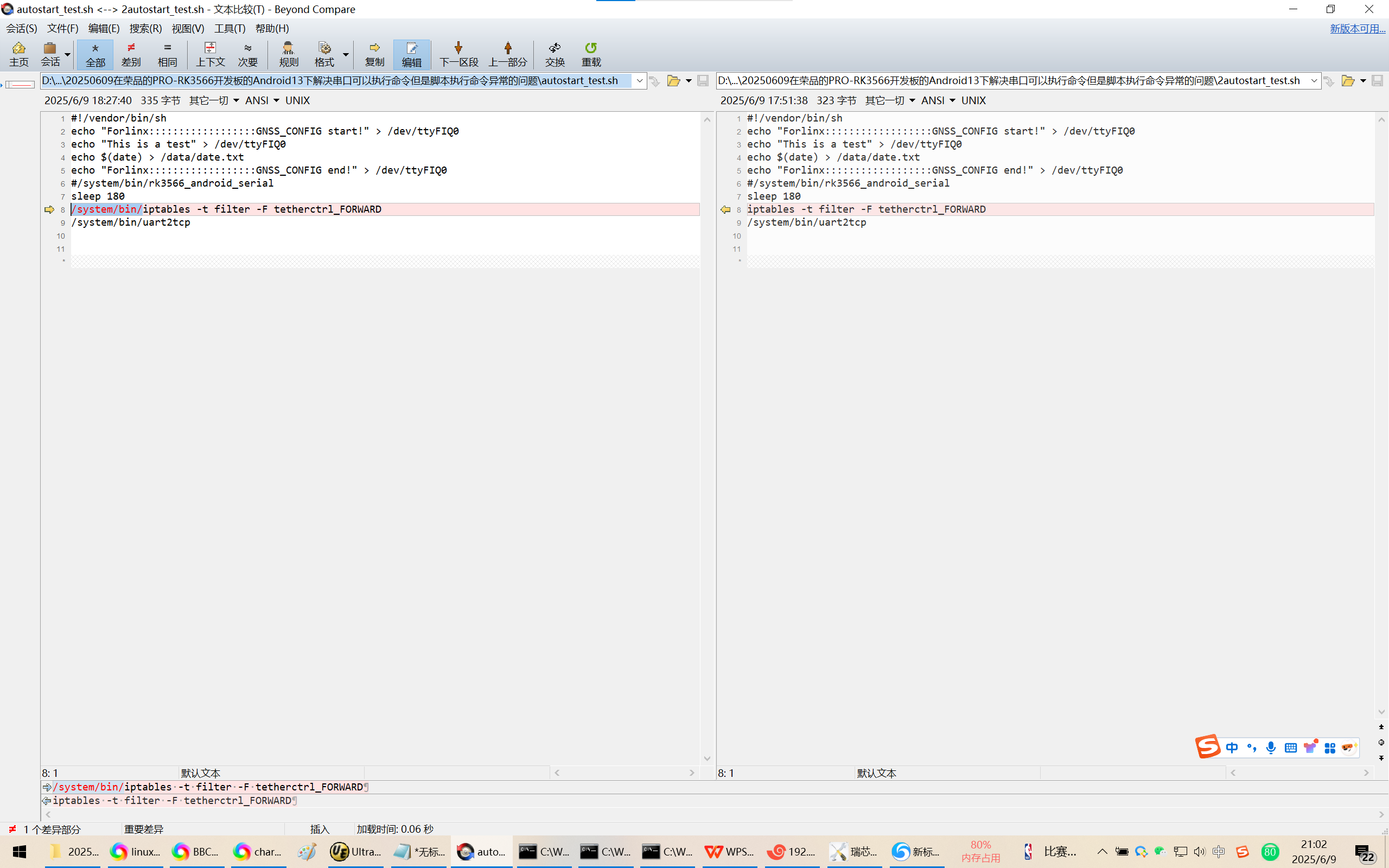
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题 2025/6/9 20:54 缘起,为了跨网段推流,千辛万苦配置好了网络参数。 但是命令iptables -t filter -F tetherctrl_FORWARD可以在调试串口/DEBUG口正确执行。…...

HTML版英语学习系统
HTML版英语学习系统 这是一个完全免费、无需安装、功能完整的英语学习工具,使用HTML CSS JavaScript实现。 功能 文本朗读练习 - 输入英文文章,系统朗读帮助练习听力和发音,适合跟读练习,模仿学习;实时词典查询 - 双…...

Unity-ECS详解
今天我们来了解Unity最先进的技术——ECS架构(EntityComponentSystem)。 Unity官方下有源码,我们下载源码后来学习。 ECS 与OOP(Object-Oriented Programming)对应,ECS是一种完全不同的编程范式与数据架构…...

【Axure高保真原型】图片列表添加和删除图片
今天和大家分享图片列表添加和删除图片的原型模板,效果包括: 点击图片列表的加号可以显示图片选择器,选择里面的图片; 选择图片后点击添加按钮,可以将该图片添加到图片列表; 鼠标移入图片列表的图片&…...
