Day56【动态规划】583.两个字符串的删除操作、72.编辑距离
583.两个字符串的删除操作
力扣题目链接/文章讲解
视频讲解
1、确定 dp 数组下标及值含义
dp[i][j]:以下标 i 为结尾的字符串 word1,和以下标 j 为结尾的字符串 word2,想要达到相等,所需要删除元素的最少次数为 dp[i][j]
2、确定递推公式
当 word1[i] == word2[j] 时:
这个时候只需要考虑怎么对 word1[0, i - 1] 和 word2[0, j - 1] 删除到相同即可
即 dp[i][j] = dp[i - 1][j - 1]
当 word1[i] != word2[j] 时:
- 可以先删除 word1[i],然后再对 word1[0, i - 1] 和 word2[0, j] 删除到相同
即 dp[i - 1][j] + 1,其中 +1 表示“先删除 word1[i]”,dp[i - 1][j] 是对 word1[0, i - 1] 和 word2[0, j] 删除到相同所需要的最少次数
- 可以先删除 word2[j],然后再对 word1[0, i] 和 word2[0, j - 1] 删除到相同
即 dp[i][j - 1] + 1,其中 +1 表示“先删除 word2[j]”,dp[i][j - 1] 是对 word1[0, i] 和 word2[0, j - 1] 删除到相同所需要的最少次数
因为求最少,这两种删除的方式所需要删除元素的最少次数取最小即为 dp 值
即 dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1)
始终别忘了我们 dp 数组的值是删除元素的最少次数!
3、dp 数组初始化
需要初始化 dp[i][0] 和 dp[0][j]
dp[i][0]:以 i 为结尾的字符串 word1,和 word2[0] 想要达到相等,所需要删除元素的最少次数
dp[0][j]:以 j 为结尾的字符串 word2,和 word1[0] 想要达到相等,所需要删除元素的最少次数
我们发现到这里,很难初始化!
怎么办呢,用我们之前的思路,更改 dp[i][j] 的定义,重新来一遍
1、确定 dp 数组下标及值含义
dp[i][j]:以下标 i - 1 为结尾的字符串 word1,和以下标 j - 1 为结尾的字符串 word2,想要达到相等,所需要删除元素的最少次数为 dp[i][j]
2、确定递推公式
还是按照我们之前的思路
当 word1[i - 1] == word2[j - 1] 时:
这个时候只需要考虑怎么对 word1[0, i - 2] 和 word2[0, j - 2] 删除到相同即可
即 dp[i][j] = dp[i - 1][j - 1]
当 word1[i - 1] != word2[j - 1] 时:
- 可以先删除 word1[i - 1],然后再对 word1[0, i - 2] 和 word2[0, j - 1] 删除到相同
即 dp[i - 1][j] + 1
- 可以先删除 word2[j],然后再对 word1[0, i] 和 word2[0, j - 1] 删除到相同
即 dp[i][j - 1] + 1
因为求最少,这两种删除的方式所需要删除元素的最少次数取最小即为 dp 值
即 dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1)
始终别忘了我们 dp 数组的值是删除元素的最少次数!
3、dp 数组初始化
需要初始化 dp[i][0] 和 dp[0][j]
dp[i][0]:以下标 i - 1 为结尾的字符串 word1,和空字符串想要达到相等,所需要删除元素的最少次数,即将 word1 中的 i 个字符(下标 0 到下标 i - 1 总共有 i 个字符)全删了,dp[i][0] = i
dp[0][j]:以下标 j - 1 为结尾的字符串 word2,和空字符串想要达到相等,所需要删除元素的最少次数,即将 word2 中的 j 个字符全删了,dp[0][j] = j
4、确定遍历顺序:从上向下,从左往右遍历填充 dp 数组
5、打印 dp 数组验证
代码如下
class Solution {
public:int minDistance(string word1, string word2) {// dp[i][j]:以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,想要达到相等,所需要删除元素的最少次数为dp[i][j],dp下标最大值-1要能达到字符串的结尾,故dp维度要比word维度多1vector<vector<int> > dp(word1.size() + 1, vector<int>(vector<int>(word2.size() + 1)));for (int i = 0; i <= word1.size(); ++i) {dp[i][0] = i; }for (int j = 0; j <= word2.size(); ++j) {dp[0][j] = j; }for (int i = 1; i <= word1.size(); ++i) { // 从上到下,从左往右填充for (int j = 1; j <= word2.size(); ++j) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1]; // 直接考虑该怎么对word1[i-2]和word2[j-2]做删除操作}else {dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);// 先删除一个,再考虑怎么对剩下的做删除操作}}}return dp[word1.size()][word2.size()];}
};本题我们真真切切体验到了,哪怕思路相同,不同定义 dp 的方式带来的代码难度也会不同
另一种思路,只要求出两个字符串的最长公共子序列长度即可,那么除了最长公共子序列之外的字符都是必须删除的,最后用两个字符串的总长度减去两个最长公共子序列的长度就是删除的最少步数
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int> > dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));for (int i = 1; i <= word1.size(); ++i) {for (int j = 1; j <= word2.size(); ++j) {if (word1[i - 1] == word2[j - 1])dp[i][j] = dp[i - 1][j - 1] + 1;elsedp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}return word1.size() + word2.size() - 2 * dp[word1.size()][word2.size()];}
};72.编辑距离
力扣题目链接/文章讲解
视频讲解
上一道题只能删除操作,这道题可以插入、删除、替换
1、确定 dp 数组下标及值含义
dp[i][j]:以下标 i - 1 为结尾的字符串 word1,和以下标 j - 1 为结尾的字符串 word2,想要达到相等,所需要的最少操作次数为 dp[i][j]
这里为什么定义以下标-1为结尾,上一道题目体验过了,就是为了方便初始化
2、确定递推公式
考虑怎么让以下标 i - 1 为结尾的字符串 word1,和以下标 j - 1 为结尾的字符串 word2 变得相同,必然涉及到比较元素
当 word1[i - 1] == word2[j - 1] 时:
这个时候只需要考虑怎么对 word1[0, i - 2] 和 word2[0, j - 2] 操作到相同即可
即 dp[i][j] = dp[i - 1][j - 1]

当 word1[i - 1] != word2[j - 1] 时:
这部分是难点!
考虑下一步可以执行三种操作
- 删除操作
- 可以先删除 word1[i - 1],然后再对 word1[0, i - 2] 和 word2[0, j - 1] 操作到相同,此时最少操作数为 dp[i - 1][j] + 1(+1 代表先执行的删除操作,dp[i - 1][j] 为对 word1[0, i - 2] 和 word2[0, j - 1] 操作到相同所需要的最少操作数)
- 可以先删除 word2[j - 1],然后再对 word1[0, i - 1] 和 word2[0, j - 1] 操作到相同,此时最少操作数为 dp[i][j - 1] + 1
- 插入操作:插入操作的次数和删除操作的次数是一样的,互为逆向操作。word2添加一个元素,相当于word1删除一个元素
我们还是推导一下来证明插入和删除操作的次数是一样的。可以先在 word1[0, i - 1] 末尾加一个 word2[i - 1],然后再对 word1[0, i - 1] 和 word2[0, j - 2] 操作到相同。此时最少操作数为 dp[i][j - 1] + 1,即删除操作中的第二种情况。

如果先在 word2[0, j - 1] 末尾加一个 word1[i - 1],然后再对 word1[0, i - 2] 和 word2[0, j - 1] 操作到相同,则对应删除操作中的第一种情况,为 dp[i - 1][j] + 1
- 替换操作
先将 word1[i - 1] 或 word2[j - 1] 替换为相同元素,然后再对 word1[0, i - 2] 和 word2[0, j - 2] 操作到相同。此时最少操作数为 dp[i - 1][j - 1] + 1(+1 代表先执行的替换操作,dp[i - 1][j - 1] 为对 word1[0, i - 2] 和 word2[0, j - 2] 操作到相同所需要的最少操作数)
综上所述,当 word1[i - 1] != word2[j - 1] 时,取上述每种操作所有情况的最小值
dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1)
if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];
}
else {dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}3、dp 数组初始化

需要初始化第一行和第一列
再回顾一下dp[i][j]的定义:
dp[i][j]:以下标 i - 1 为结尾的字符串 word1,和以下标 j - 1 为结尾的字符串 word2,最近编辑距离为 dp[i][j]
那么 dp[i][0] 和 dp[0][j] 表示什么呢?
dp[i][0] :以下标 i - 1 为结尾的字符串 word1,和空字符串 word2,最近编辑距离为 dp[i][0]
那么 dp[i][0] 就应该是 i,对 word1[0, i - 1] 里的元素全部做删除操作,即:dp[i][0] = i
同理dp[0][j] = j
4、确定遍历顺序
dp[i][j] 是依赖左方,上方和左上方元素,需要从左到右从上到下去遍历填充
5、打印 dp 数组验证
代码如下
class Solution {
public:int minDistance(string word1, string word2) {// 定义dp数组,注意dp数组的大小vector<vector<int> > dp(word1.size() + 1, vector<int>(word2.size() + 1));// 初始化for (int i = 0; i <= word1.size(); ++i) {dp[i][0] = i;}for (int j = 0; j <= word2.size(); ++j) {dp[0][j] = j;}for (int i = 1; i <= word1.size(); ++i) {for (int j = 1; j <= word2.size(); ++j) {if (word1[i - 1] == word2[j - 1]) // 直接对word1[0,i-2]和word2[0,j-2]操作dp[i][j] = dp[i - 1][j - 1];else {// 先删除或添加,再对剩下的操作、先替换,再对剩下的操作dp[i][j] = min({dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1});}}}return dp[word1.size()][word2.size()];}
};回顾总结
编辑距离问题结束
总结一下最近的题目,都是操作两个字符串,定义 dp 数组和确定递推公式都挺难的
确定递推公式时,一般需要考虑比较元素相等或不相等两种情况
动态规划分解为子问题的思想需要贯穿(先执行了某个操作后,后续操作是否可以由其他 dp 值推导而来)
相关文章:

Day56【动态规划】583.两个字符串的删除操作、72.编辑距离
583.两个字符串的删除操作 力扣题目链接/文章讲解 视频讲解 1、确定 dp 数组下标及值含义 dp[i][j]:以下标 i 为结尾的字符串 word1,和以下标 j 为结尾的字符串 word2,想要达到相等,所需要删除元素的最少次数为 dp[i][j] 2、…...

Arnold图像置乱的MATLAB实现
这件事情的起因是这样的,我需要研究一下各种图像置乱的算法。然后在知乎上找到了一篇关于Arnold变化的文章,但是呢,这个人实际上是卖资料,代做大作业的。详细的代码根部不给你,则给我气坏了,必须要手动实现…...
ASP.NET Core
1. 入口文件 一个应用程序总有一个入口文件,是应用启动代码开始执行的地方,这里往往也会涉及到应用的各种配置。当我们接触到一个新框架的时候,可以从入口文件入手,了解入口文件,能够帮助我们更好地理解应用的相关配置…...
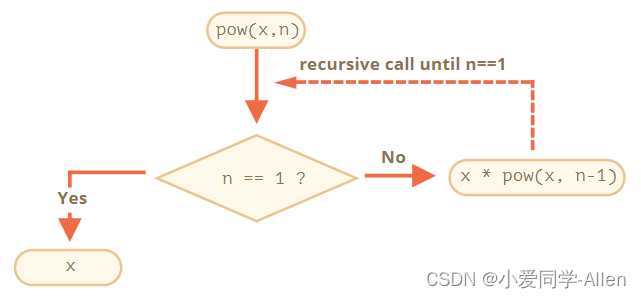
javascript基础二十二:举例说明你对尾递归的理解,有哪些应用场景
一、递归 递归(英语:Recursion) 在数学与计算机科学中,是指在函数的定义中使用函数自身的方法 在函数内部,可以调用其他函数。如果一个函数在内部调用自身本身,这个函数就是递归函数 其核心思想是把一个大型…...
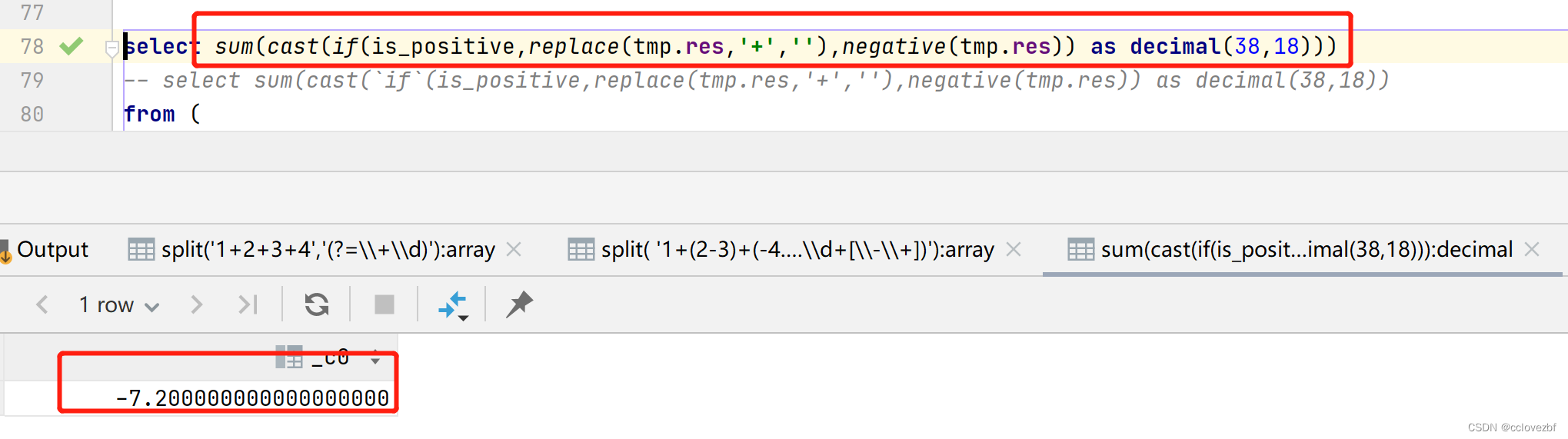
hive中如何计算字符串中表达式
比如 select 1(2-3)(-4.1-3.1)-(4-3)-(-3.34.3)-1 col ,1(2-3)(-4.1-3.1)-(4-3)-(-3.34.3)-1 result \ 现在的需求式 给你一个字符串如上述col 你要算出result。 前提式 只有和-的运算,而且只有嵌套一次 -(4-3)没有 -(-4(3-(31)))嵌套多次。 第一步我们需要将运…...

如何将maven项目改为springboot项目?
将 Maven 项目转换为 Spring Boot 项目需要进行以下步骤: 1. 在 Maven 项目中添加 Spring Boot 的依赖。可以通过在 pom.xml 文件中添加以下依赖来实现: <dependency> <groupId>org.springframework.boot</groupId> <artifactId>…...
:哈希查找)
Java与查找算法(5):哈希查找
一、哈希查找 哈希查找,也称为散列查找,是一种基于哈希表的查找算法。哈希表是一种数据结构,它将键(key)映射到值(value),使得查找某个键对应的值的时间复杂度为O(1)。哈希查找的过…...
Vercel部署个人博客
vercel 部署静态资源网站极其方便简单,并且有可观的访问速度,最主要的是免费部署。 如果你还没有尝试的话,强烈建议去使用一下。 演示博客演示http://202271.xyz/?vercel vercel 介绍 注册账号 进入Vercel官网https://vercel.com&#x…...
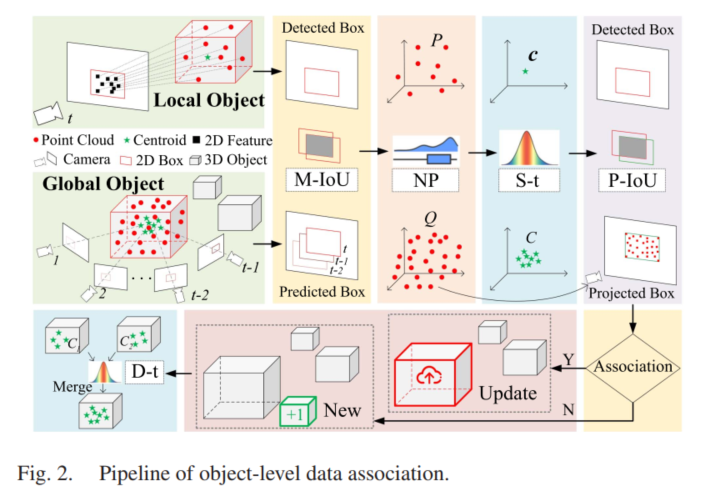
【论文阅读】An Object SLAM Framework for Association, Mapping, and High-Level Tasks
一、系统概述 这篇文章是一个十分完整的物体级SLAM框架,偏重于建图及高层应用,在前端的部分使用了ORBSLAM作为基础框架,用于提供点云以及相机的位姿,需要注意的是,这篇文章使用的是相机,虽然用的是点云这个…...

《metasploit渗透测试魔鬼训练营》学习笔记第六章--客户端渗透
四.客户端攻击 客户端攻击与服务端攻击有个显著不同的标识,就是攻击者向用户主机发送的恶意数据不会直接导致用户系统中的服务进程溢出,而是需要结合一些社会工程学技巧,诱使客户端用户去访问这些恶意数据,间接发生攻击。 4.1客户…...

华为OD机试真题 Java 实现【Linux 发行版的数量】【2023Q1 100分】
一、题目描述 Linux 操作系统有多个发行版,distrowatch.com 提供了各个发行版的资料。这些发行版互相存在关联,例如 Ubuntu 基于 Debian 只开发而 Mint 又基于 Ubuntu 开发,那么我们认为 Mint 同 Debian 也存在关联。 发行版集是一个或多个相关存在关联的操作系统发行版,…...
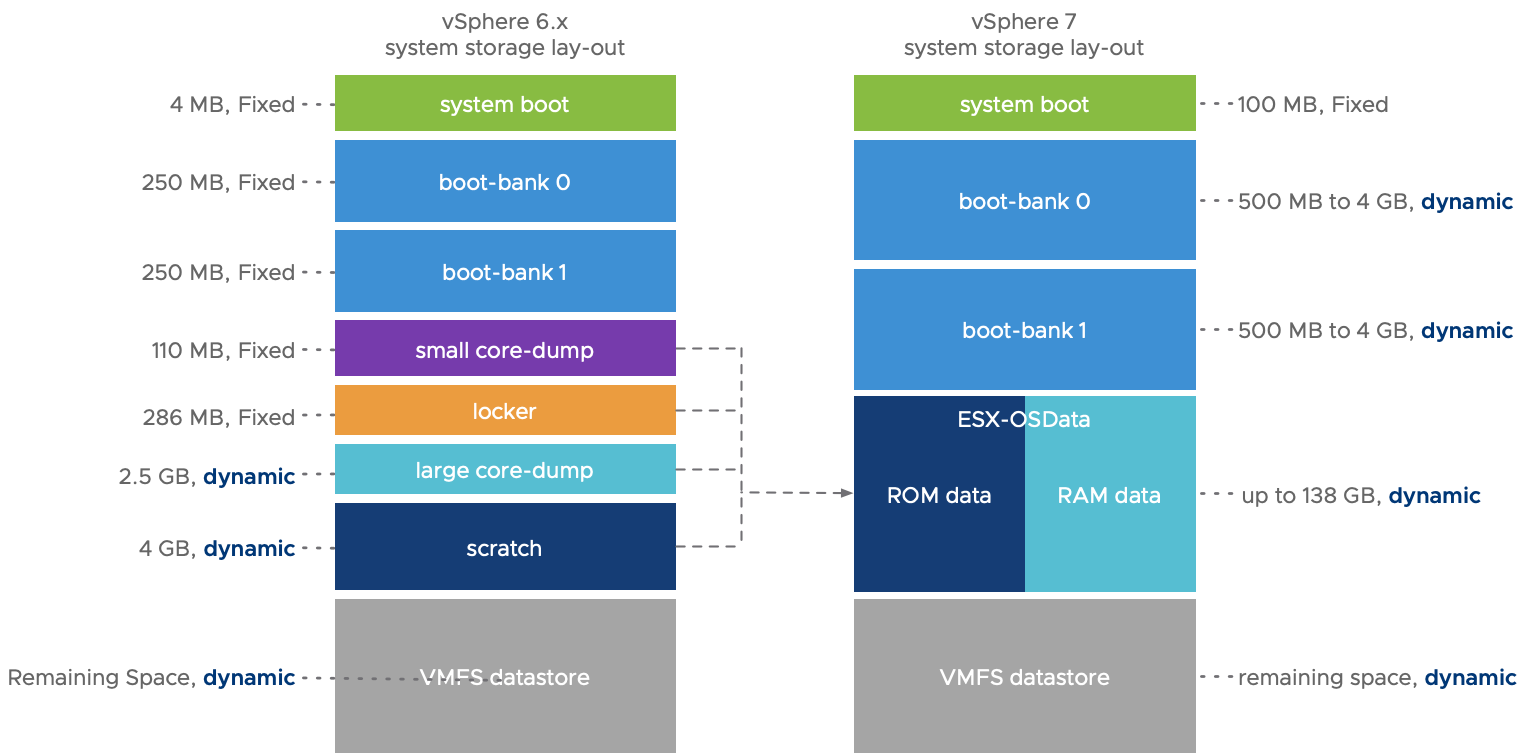
VMware ESXi 8.0U1a macOS Unlocker OEM BIOS (标准版和厂商定制版)
VMware ESXi 8.0 Update 1a macOS Unlocker & OEM BIOS (标准版和厂商定制版) ESXi 8.0U1 标准版,Dell HPE 联想 浪潮 定制版 请访问原文链接: https://sysin.org/blog/vmware-esxi-8-u1-oem/,查看最新版。原创作品,转载请保…...

Effective STL_读书笔记
Effective STL 1. 容器条例01:慎重选择容器类型条例02:不要试图编写独立于容器类型的代码条例03:确保容器中对象的拷贝正确而高效条例04:调用empty而不是检查size()是否为空条例05:区间成员函数优先于与之对应的单元素…...
通过yum:mysql5.6-msyql5.7-mysql8.0升级之路
一 前言 mysql的yum源 https://dev.mysql.com/downloads/repo/yum/ https://dev.mysql.com/get/mysq57-community-release-el7-7.noarch.rpm服务器信息 2c2g40GB [rootlocalhost ~]# cat /etc/redhat-release CentOS Linux release 7.9.2009 (Core) [rootlocalhost ~]# una…...

C语言数据存储 — 整型篇
C语言数据存储 — 整型篇 前言1. 数据类型介绍1.1 类型的基本分类 2. 整型在内存中的存储2.1 原码、反码、补码2.1.1 为什么数据存放在内存中存放的是补码 2.2 大小端介绍2.2.1 什么是大小端?2.2.2 为什么有大端和小端?2.2.3 一道百度系统工程师笔试题 3…...

高级Excel功能教程_编程入门自学教程_菜鸟教程-免费教程分享
教程简介 Excel是办公室自动化中非常重要的一款软件,Excel函数则是Excel中的内置函数。Excel函数共包含11类,分别是数据库函数、日期与时间函数、工程函数、财务函数、信息函数、逻辑函数、查询和引用函数、数学和三角函数、统计函数、文本函数以及用户…...

ChatGPT会取代低代码开发平台吗?
编程作为一种高端技能,向来是高收入高科技的代名词。近期,伴随着ChatGPT在全球的爆火,过去通过窗口“拖拉拽”的所见即所得方式的低代码开发模式,在更加智能和更低成本的AI搅局之下,又面临了更深层次的影响。 低代码平…...

Linux :: 文件内容操作【5】:echo 指令 与 输入重定向、输出重定向、追加重定向在文件内容写入中的简单用法!
前言:本篇是 Linux 基本操作篇章的内容! 笔者使用的环境是基于腾讯云服务器:CentOS 7.6 64bit。 学习集: C 入门到入土!!!学习合集Linux 从命令到网络再到内核!学习合集 说明&#x…...

【RocketMQ】重试机制及死信消息处理
【RocketMQ】重试机制及死信消息处理 文章目录 【RocketMQ】重试机制及死信消息处理1. 重试机制1.1 生产者重试1.2 消费者重试1.2.1 死信队列 参考文档: 官方文档 1. 重试机制 1.1 生产者重试 rocketmq生产者发送消息失败默认重试2次(同步发送为2次,异…...
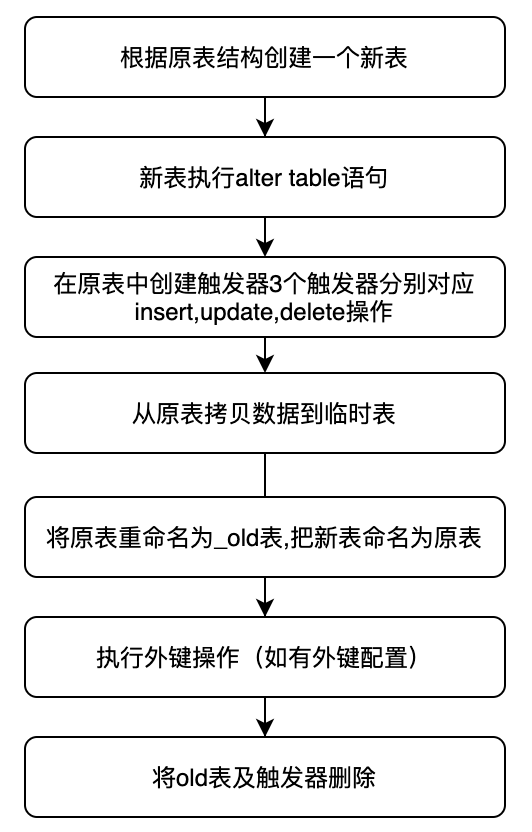
Mysql DDL执行方式-pt-osc介绍 | 京东云技术团队
1 引言 大家好,接着上次和大家一起学习了《MySQL DDL执行方式-Online DDL介绍》,那么今天接着和大家一起学习另一种MySQL DDL执行方式之pt-soc。 在MySQL使用过程中,根据业务的需求对表结构进行变更是个普遍的运维操作,这些称为…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
