Arnold图像置乱的MATLAB实现
这件事情的起因是这样的,我需要研究一下各种图像置乱的算法。然后在知乎上找到了一篇关于Arnold变化的文章,但是呢,这个人实际上是卖资料,代做大作业的。详细的代码根部不给你,则给我气坏了,必须要手动实现一下,打击他卖资料的嚣张气焰。
文章目录
- 代码编写
- 周期分析
简书上的一个作者写的还是相当不错的,这是网址链接。
Arnold 变换是俄国数学家 Vladimir I. Arnold提出的一种变换,一幅 N × N N ×N N×N 的数字图像的二维Arnold
变换定义为:
[ x ′ y ′ ] = [ a b c d ] n [ x y ] m o d N \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]^{n}\left[\begin{array}{l} x \\ y \end{array}\right] \bmod N [x′y′]=[acbd]n[xy]modN
注意: x x x, y y y 是原图像的像素坐标, x ′ x' x′, y ′ y' y′ 是变换后的像素坐标。保证 ∣ a d − b c ∣ = 1 |ad-bc|=1 ∣ad−bc∣=1,如置换矩阵系数设为 a = b = 1 a=b=1 a=b=1, c = 2 c=2 c=2, d = 3 d=3 d=3,置换次数 n = 20 n=20 n=20,则他们被当作密钥 key,用于解密。Arnold 变换的图像类型只能是 N × N N\times N N×N 的图片。
我从网络上面下载了一朵花的图片,如下

代码编写
close all;
%图像加密置乱:
a=imread('flower.png'); %取预处理图像
a=a(1:226,1:226,1:3); %截取成正方形
R=a(:,:,1); %取图像的R层像素
G=a(:,:,2); %取图像的G层像素
B=a(:,:,3); %取图像的B层像素
figure;
subplot(2,2,1);imshow(a);title('original');
subplot(2,2,2);imshow(R);title('R');
subplot(2,2,3);imshow(G);title('G');
subplot(2,2,4);imshow(B);title('B');%三个不同密钥
keyR=10;keyG=20;keyB=30;aR=arnold(R,keyR,1);aG=arnold(G,keyG,1);aB=arnold(B,keyB,1);%对各层用不同的密钥加密
figure;
subplot(2,2,1);imshow(aR);title('aR');%加密后的图像
subplot(2,2,2);imshow(aG);title('aG');
subplot(2,2,3);imshow(aB);title('aB');
aa=cat(3,aR,aG,aB); %各层加密后在合成彩色图像
subplot(2,2,4); imshow(aa); title(' Permuted');%RGB图像加密后的结果
imwrite(aa,'a_flower.bmp');%图像解密
R=arnold(aR,keyR,0);G=arnold(aG,keyG,0);B=arnold(aB,keyB,0);%对各层用不同的密钥加密
R=uint8(R);G=uint8(G);B=uint8(B);
figure;
subplot(2,2,1);imshow(R);title('R');
subplot(2,2,2);imshow(G);title('G');
subplot(2,2,3);imshow(B);title('B');
flower=cat(3,R,G,B); %各层加密后在合成彩色图像
subplot(2,2,4); imshow(flower); title('恢复的图案');%RGB图像解密后的结果



arnold.m 是一个单独的函数文件
function img=arnold(img,key,pon)
%img是原始图片
%Key是输入的密钥
%a,b是置乱矩阵里面的值
%pon表示正变换或者反变换
[h, w]=size(img);
a=2;b=3;
img_new = zeros(h,w); %[h, w]=size(img)
N=h;if(pon)%正变换for i=1:key %n为置乱轮数for y=1:hfor x=1:wxx=mod((x-1)+b*(y-1),N)+1; %a,b可提前指定yy=mod(a*(x-1)+(a*b+1)*(y-1),N)+1;img_new(yy,xx)=img(y,x);endendimg=img_new;end
else%反变换for i=1:keyfor y=1:hfor x=1:wxx=mod((a*b+1)*(x-1)-b*(y-1),N)+1;yy=mod(-a*(x-1)+(y-1),N)+1 ;img_new(yy,xx)=img(y,x);endendimg=img_new;end
end
周期分析
我现在知道为什么了,因为广义的 Arnold 算法根本没有周期性。
理论上下面的代码是可以计算周期的,但是我跑到了 1 0 7 10^7 107 的数量级,依然没有闭环。等以后如果弄明白了再来讲吧。
%计算Arnold变换的周期T可以利用一下MATLAB程序来实现。x = 1; y = 1;N = 4; %N × N为128 ×128的图像
T = 1;
t = x; x = x + y; y = 2*t+3*y;
while x~= 1 || y~= 1T = T + 1;if x >Nx =mod ( x,N) ;endif y >Ny =mod ( y,N) ;endt = x; x = x + y; y = 2*t+3*y;
endT %所得的T值即为Arnold变换的周期
相关文章:

Arnold图像置乱的MATLAB实现
这件事情的起因是这样的,我需要研究一下各种图像置乱的算法。然后在知乎上找到了一篇关于Arnold变化的文章,但是呢,这个人实际上是卖资料,代做大作业的。详细的代码根部不给你,则给我气坏了,必须要手动实现…...
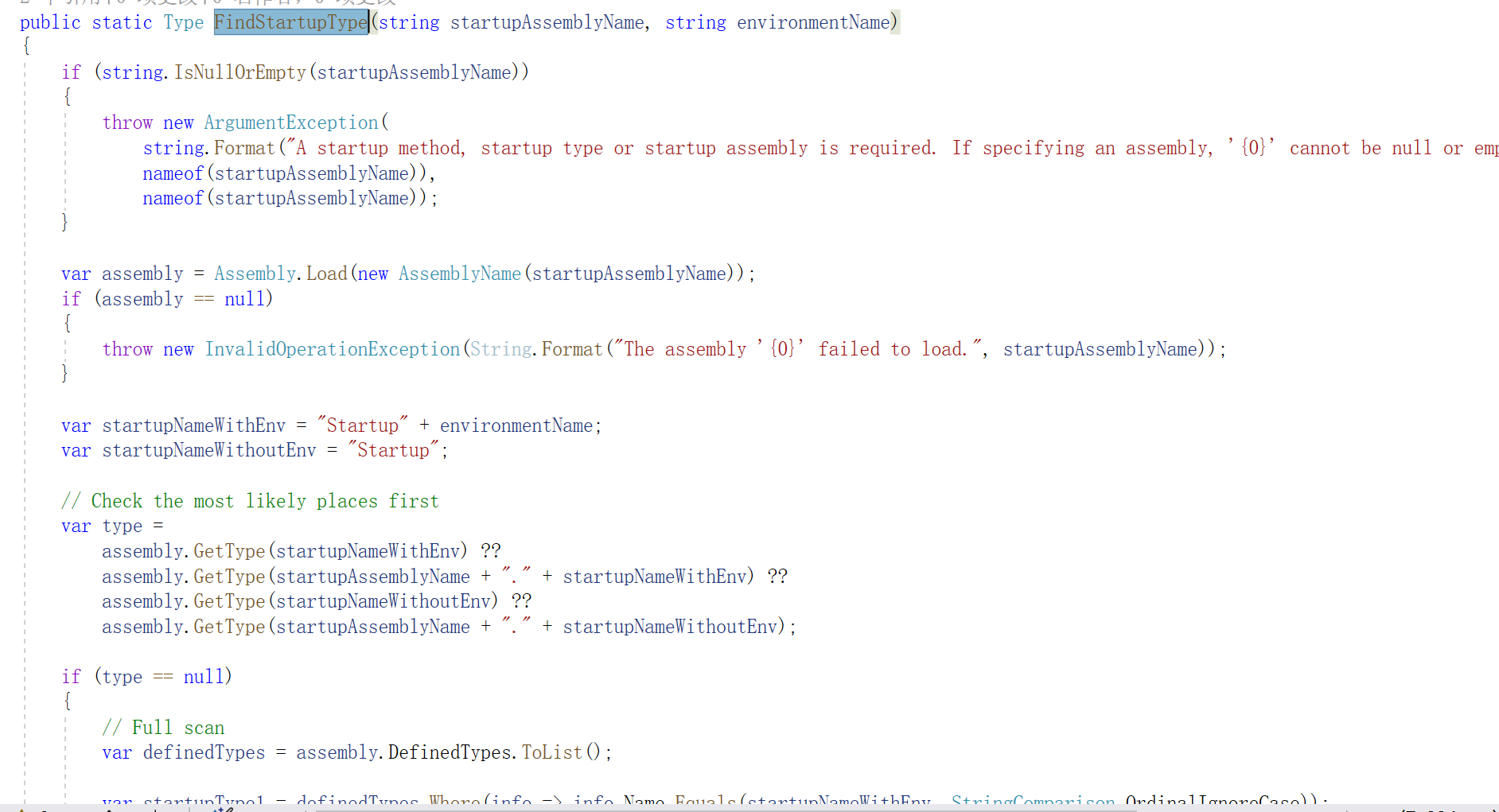
ASP.NET Core
1. 入口文件 一个应用程序总有一个入口文件,是应用启动代码开始执行的地方,这里往往也会涉及到应用的各种配置。当我们接触到一个新框架的时候,可以从入口文件入手,了解入口文件,能够帮助我们更好地理解应用的相关配置…...
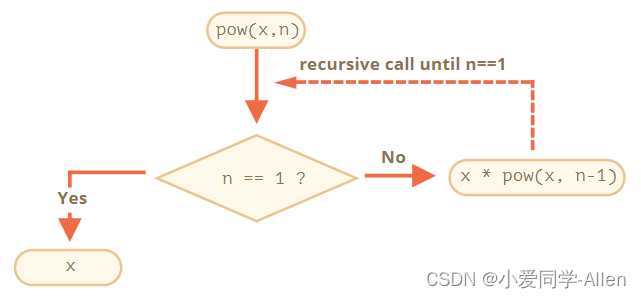
javascript基础二十二:举例说明你对尾递归的理解,有哪些应用场景
一、递归 递归(英语:Recursion) 在数学与计算机科学中,是指在函数的定义中使用函数自身的方法 在函数内部,可以调用其他函数。如果一个函数在内部调用自身本身,这个函数就是递归函数 其核心思想是把一个大型…...
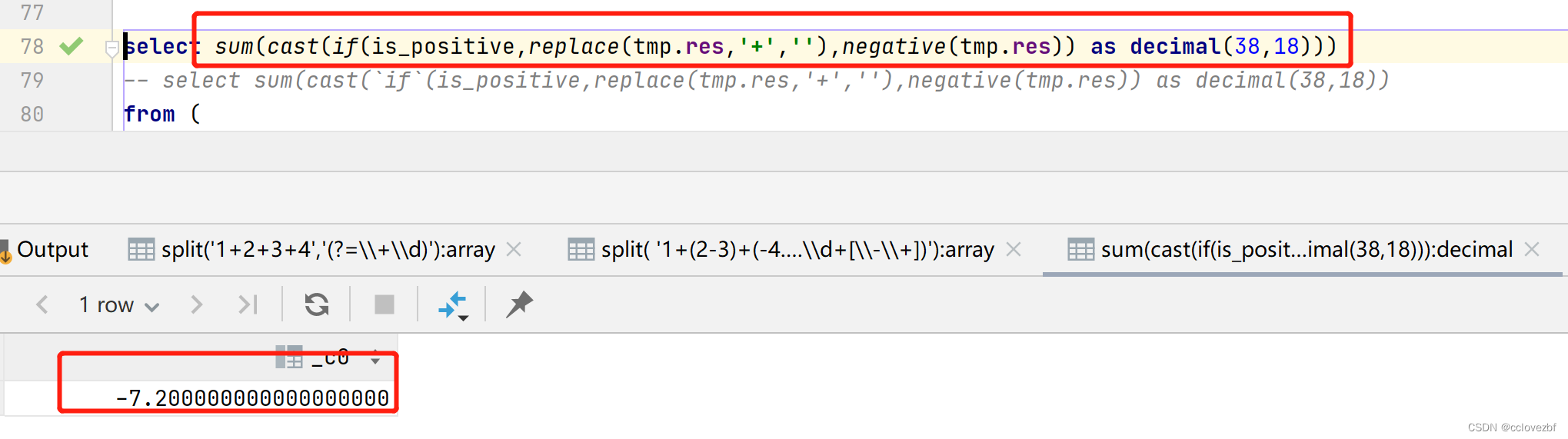
hive中如何计算字符串中表达式
比如 select 1(2-3)(-4.1-3.1)-(4-3)-(-3.34.3)-1 col ,1(2-3)(-4.1-3.1)-(4-3)-(-3.34.3)-1 result \ 现在的需求式 给你一个字符串如上述col 你要算出result。 前提式 只有和-的运算,而且只有嵌套一次 -(4-3)没有 -(-4(3-(31)))嵌套多次。 第一步我们需要将运…...

如何将maven项目改为springboot项目?
将 Maven 项目转换为 Spring Boot 项目需要进行以下步骤: 1. 在 Maven 项目中添加 Spring Boot 的依赖。可以通过在 pom.xml 文件中添加以下依赖来实现: <dependency> <groupId>org.springframework.boot</groupId> <artifactId>…...
:哈希查找)
Java与查找算法(5):哈希查找
一、哈希查找 哈希查找,也称为散列查找,是一种基于哈希表的查找算法。哈希表是一种数据结构,它将键(key)映射到值(value),使得查找某个键对应的值的时间复杂度为O(1)。哈希查找的过…...
Vercel部署个人博客
vercel 部署静态资源网站极其方便简单,并且有可观的访问速度,最主要的是免费部署。 如果你还没有尝试的话,强烈建议去使用一下。 演示博客演示http://202271.xyz/?vercel vercel 介绍 注册账号 进入Vercel官网https://vercel.com&#x…...
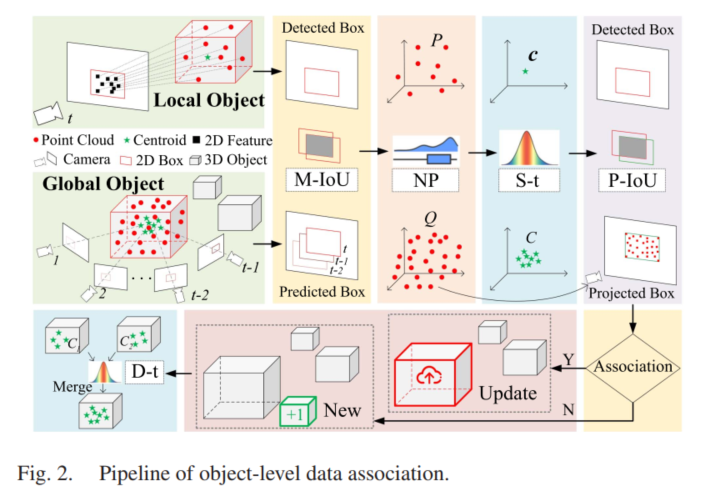
【论文阅读】An Object SLAM Framework for Association, Mapping, and High-Level Tasks
一、系统概述 这篇文章是一个十分完整的物体级SLAM框架,偏重于建图及高层应用,在前端的部分使用了ORBSLAM作为基础框架,用于提供点云以及相机的位姿,需要注意的是,这篇文章使用的是相机,虽然用的是点云这个…...

《metasploit渗透测试魔鬼训练营》学习笔记第六章--客户端渗透
四.客户端攻击 客户端攻击与服务端攻击有个显著不同的标识,就是攻击者向用户主机发送的恶意数据不会直接导致用户系统中的服务进程溢出,而是需要结合一些社会工程学技巧,诱使客户端用户去访问这些恶意数据,间接发生攻击。 4.1客户…...

华为OD机试真题 Java 实现【Linux 发行版的数量】【2023Q1 100分】
一、题目描述 Linux 操作系统有多个发行版,distrowatch.com 提供了各个发行版的资料。这些发行版互相存在关联,例如 Ubuntu 基于 Debian 只开发而 Mint 又基于 Ubuntu 开发,那么我们认为 Mint 同 Debian 也存在关联。 发行版集是一个或多个相关存在关联的操作系统发行版,…...
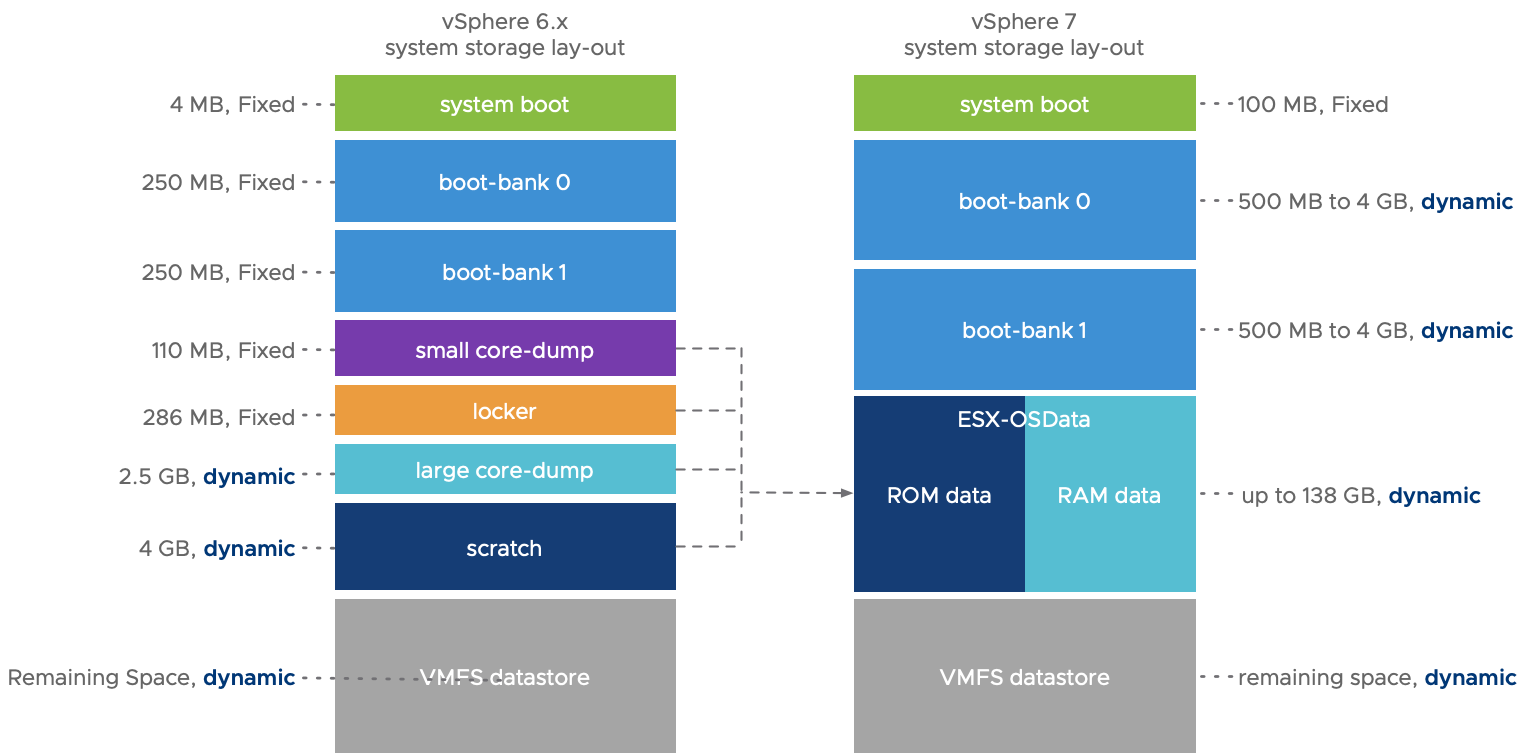
VMware ESXi 8.0U1a macOS Unlocker OEM BIOS (标准版和厂商定制版)
VMware ESXi 8.0 Update 1a macOS Unlocker & OEM BIOS (标准版和厂商定制版) ESXi 8.0U1 标准版,Dell HPE 联想 浪潮 定制版 请访问原文链接: https://sysin.org/blog/vmware-esxi-8-u1-oem/,查看最新版。原创作品,转载请保…...

Effective STL_读书笔记
Effective STL 1. 容器条例01:慎重选择容器类型条例02:不要试图编写独立于容器类型的代码条例03:确保容器中对象的拷贝正确而高效条例04:调用empty而不是检查size()是否为空条例05:区间成员函数优先于与之对应的单元素…...
通过yum:mysql5.6-msyql5.7-mysql8.0升级之路
一 前言 mysql的yum源 https://dev.mysql.com/downloads/repo/yum/ https://dev.mysql.com/get/mysq57-community-release-el7-7.noarch.rpm服务器信息 2c2g40GB [rootlocalhost ~]# cat /etc/redhat-release CentOS Linux release 7.9.2009 (Core) [rootlocalhost ~]# una…...

C语言数据存储 — 整型篇
C语言数据存储 — 整型篇 前言1. 数据类型介绍1.1 类型的基本分类 2. 整型在内存中的存储2.1 原码、反码、补码2.1.1 为什么数据存放在内存中存放的是补码 2.2 大小端介绍2.2.1 什么是大小端?2.2.2 为什么有大端和小端?2.2.3 一道百度系统工程师笔试题 3…...

高级Excel功能教程_编程入门自学教程_菜鸟教程-免费教程分享
教程简介 Excel是办公室自动化中非常重要的一款软件,Excel函数则是Excel中的内置函数。Excel函数共包含11类,分别是数据库函数、日期与时间函数、工程函数、财务函数、信息函数、逻辑函数、查询和引用函数、数学和三角函数、统计函数、文本函数以及用户…...

ChatGPT会取代低代码开发平台吗?
编程作为一种高端技能,向来是高收入高科技的代名词。近期,伴随着ChatGPT在全球的爆火,过去通过窗口“拖拉拽”的所见即所得方式的低代码开发模式,在更加智能和更低成本的AI搅局之下,又面临了更深层次的影响。 低代码平…...

Linux :: 文件内容操作【5】:echo 指令 与 输入重定向、输出重定向、追加重定向在文件内容写入中的简单用法!
前言:本篇是 Linux 基本操作篇章的内容! 笔者使用的环境是基于腾讯云服务器:CentOS 7.6 64bit。 学习集: C 入门到入土!!!学习合集Linux 从命令到网络再到内核!学习合集 说明&#x…...

【RocketMQ】重试机制及死信消息处理
【RocketMQ】重试机制及死信消息处理 文章目录 【RocketMQ】重试机制及死信消息处理1. 重试机制1.1 生产者重试1.2 消费者重试1.2.1 死信队列 参考文档: 官方文档 1. 重试机制 1.1 生产者重试 rocketmq生产者发送消息失败默认重试2次(同步发送为2次,异…...
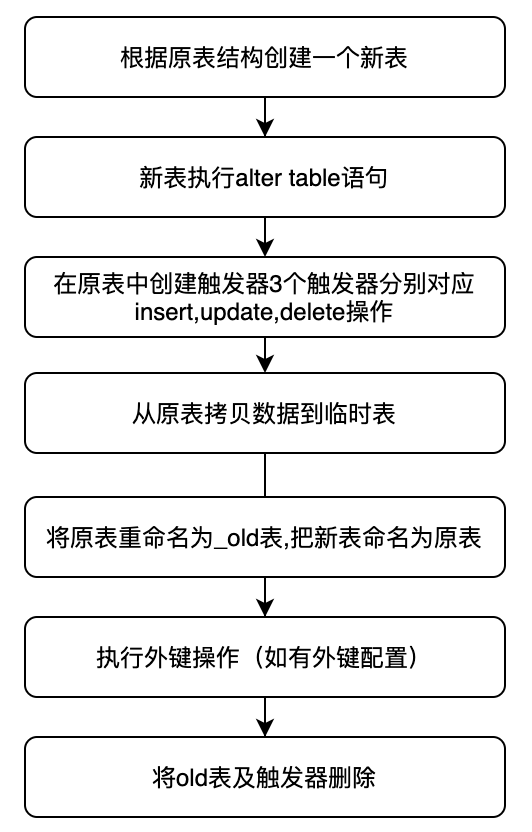
Mysql DDL执行方式-pt-osc介绍 | 京东云技术团队
1 引言 大家好,接着上次和大家一起学习了《MySQL DDL执行方式-Online DDL介绍》,那么今天接着和大家一起学习另一种MySQL DDL执行方式之pt-soc。 在MySQL使用过程中,根据业务的需求对表结构进行变更是个普遍的运维操作,这些称为…...
C++ stack容器介绍
🤔stack容器介绍: 📖 stack是一种数据结构,也可以被称为堆栈。它是一个容器,只允许在最顶层进行插入和删除,并且只能访问最后一个插入的元素。这个元素称为栈顶。所有新插入的元素都被放置在栈顶上面&#…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
