当前位置： 首页 > news >正文

「HTML和CSS入门指南」p 标签详解

news 2025/10/27 3:27:36

<p> 标签是什么？

·HTML5 中的 <p> 标签是用于定义段落的标签。它可以用来标记文章、新闻等长篇内容中的段落，并且可以与其他 HTML 元素配合使用。

<p> 标签的语法和属性

<p> 标签的语法非常简单，只需要在 HTML 文件中插入 <p> 和 </p> 标签即可。例如：

<p>这是一个段落。</p>

我们还可以为 <p> 标签设置一些属性，以改变段落的样式，如文本对齐、颜色、字体大小等。以下是一些常用的 <p> 标签属性：

  • align：定义段落的水平对齐方式，可选值包括 left、center 和 right。
  • style：定义段落的 CSS 样式，可以包含多个属性和值，例如 style="color:red;font-size:16px;"。
  • class：定义段落的类名，可以用于后续的 CSS 样式控制。
  • id：定义段落的唯一标识符，可以用于后续的 JavaScript 操作。

<p&

相关文章：

「HTML和CSS入门指南」p 标签详解

<p> 标签是什么？ HTML5 中的 <p> 标签是用于定义段落的标签。它可以用来标记文章、新闻等长篇内容中的段落，并且可以与其他 HTML 元素配合使用。 <p> 标签的语法和属性 <p> 标签的语法非常简单，只需要在 HTML 文件中插入 <p> 和 </p>…...

编程日记 2023/6/6 3:19:18

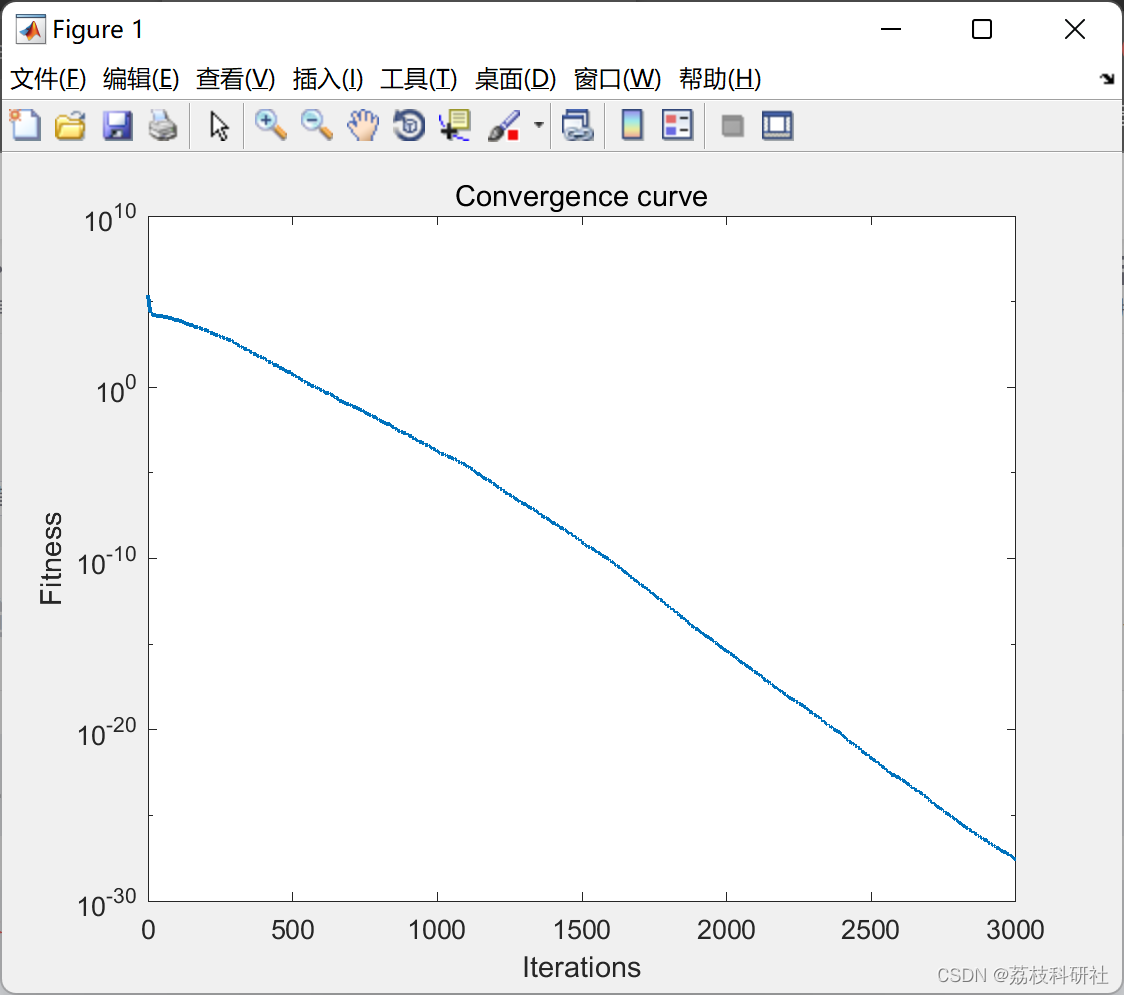
【单目标优化算法】孔雀优化算法（Matlab代码实现）

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 ⛳️座右铭&a…...

编程日记 2023/6/6 3:14:16

chatgpt赋能python：Python同一行多个语句：如何提高你的编程效率？

Python同一行多个语句&#xff1a;如何提高你的编程效率&#xff1f; Python是一种优雅的编程语言&#xff0c;拥有简洁易懂的语法&#xff0c;可以帮助你快速编写可以在各种领域使用的高级代码。其中&#xff0c;Python同一行多个语句&#xff0c;是一种可以大大提高编程效率…...

编程日记 2023/6/6 3:09:15

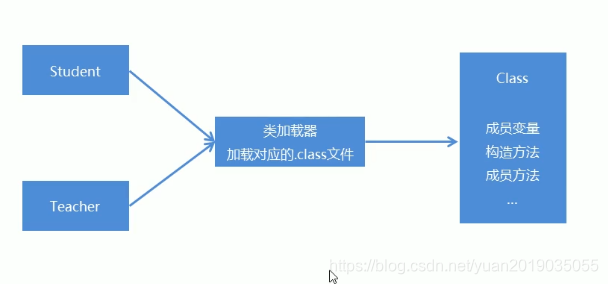
Java反射概述

2 反射 2.1 反射概述 Java反射机制：是指在运行时去获取一个类的变量和方法信息。然后通过获取到的信息来创建对象,调用方法的一种机制。由于这种动态性,可以极大的增强程序的灵活性,程序不用在编译期就完成确定,在运行期仍然可以扩展2.2 反射获取Class类的对象 我们要想通过反…...

编程日记 2023/6/6 3:04:14

《网络是怎样连接的》(一)

第一章web浏览器 简介 首先输入网址URL&#xff0c;浏览器进行解析&#xff0c;将我们需要哪些数据告诉服务器。浏览器向服务器发送消息&#xff0c;必须告诉操作系统的接收方的IP地址&#xff0c;所以浏览器先查出web服务器的IP地址&#xff0c;向DNS服务器查询域名对应的IP…...

编程日记 2023/6/6 2:59:13

Flink on yarn任务日志怎么看

1、jobmanager日志 在yarn上可以直接看 2、taskmanager日志 在flink的webui中可以看&#xff0c;但是flink任务失败后&#xff0c;webui就不存在了&#xff0c;那怎么看&#xff1f; 这是jobmanager的地址 hadoop02:19888/jobhistory/logs/hadoop02:45454/container_e03_16844…...

编程日记 2023/6/6 2:54:12

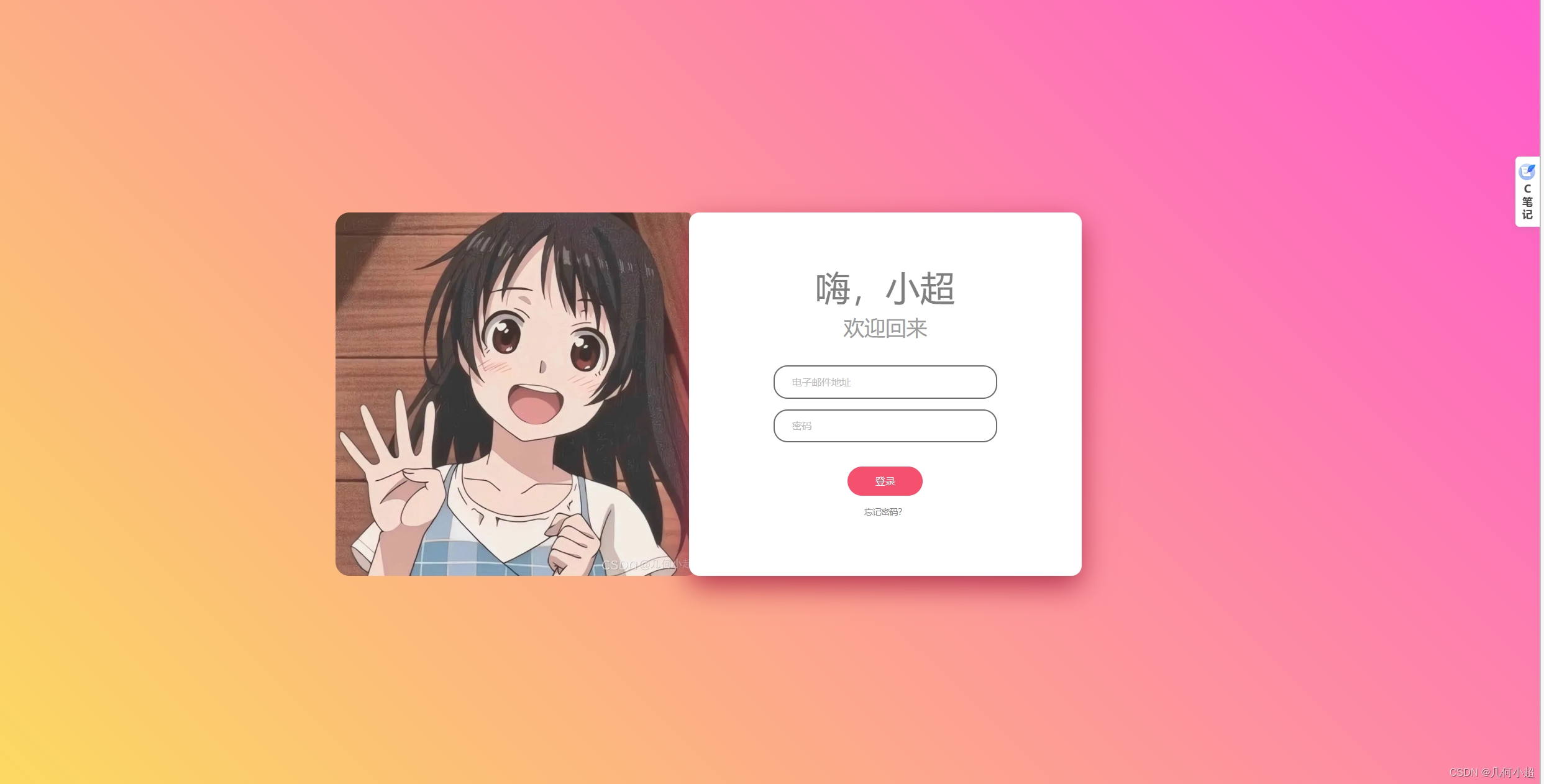
二次元的登录界面

今天还是继续坚持写博客&#xff0c;然后今天给大家带来比较具有二次元风格的登录界面&#xff0c;也只是用html和css来写的&#xff0c;大家可以来看看&#xff01; 个人名片&#xff1a; &#x1f60a;作者简介&#xff1a;一名大一在校生&#xff0c;web前端开发专业 &…...

编程日记 2023/6/6 2:49:11

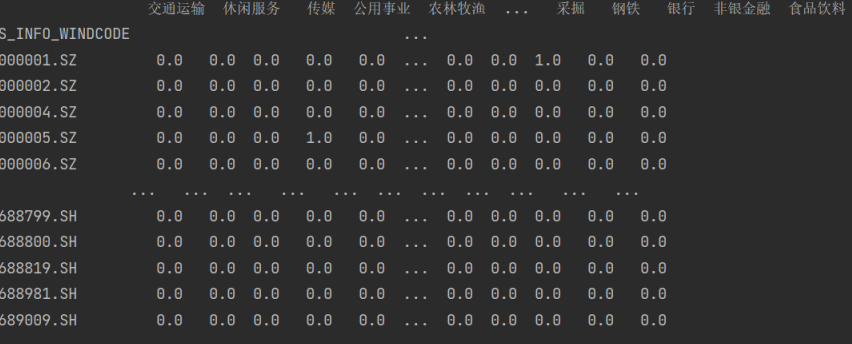
2. 量化多因子数据清洗——去极值、标准化、正交化、中性化

一、去极值 1. MAD MAD&#xff08;mean absolute deviation&#xff09;又称为绝对值差中位数法&#xff0c;是一种先需计算所有因子与平均值之间的距离总和来检测离群值的方法. def extreme_MAD(rawdata, n): median rawdata.quantile(0.5) # 找出中位数 new_median (abs(…...

编程日记 2023/6/6 2:44:10

皮卡丘反射型XSS

1.反射型xss(get) 进入反射型xss(get)的关卡&#xff0c;我们可以看到如下页面 先输入合法数据查看情况&#xff0c;例如输入“kobe” 再随便输入一个&#xff0c;比如我舍友的外号“xunlei”&#xff0c;“666”&#xff0c;嘿嘿嘿 F12查看源代码&#xff0c;发现你输入的数…...

编程日记 2023/6/6 2:39:09

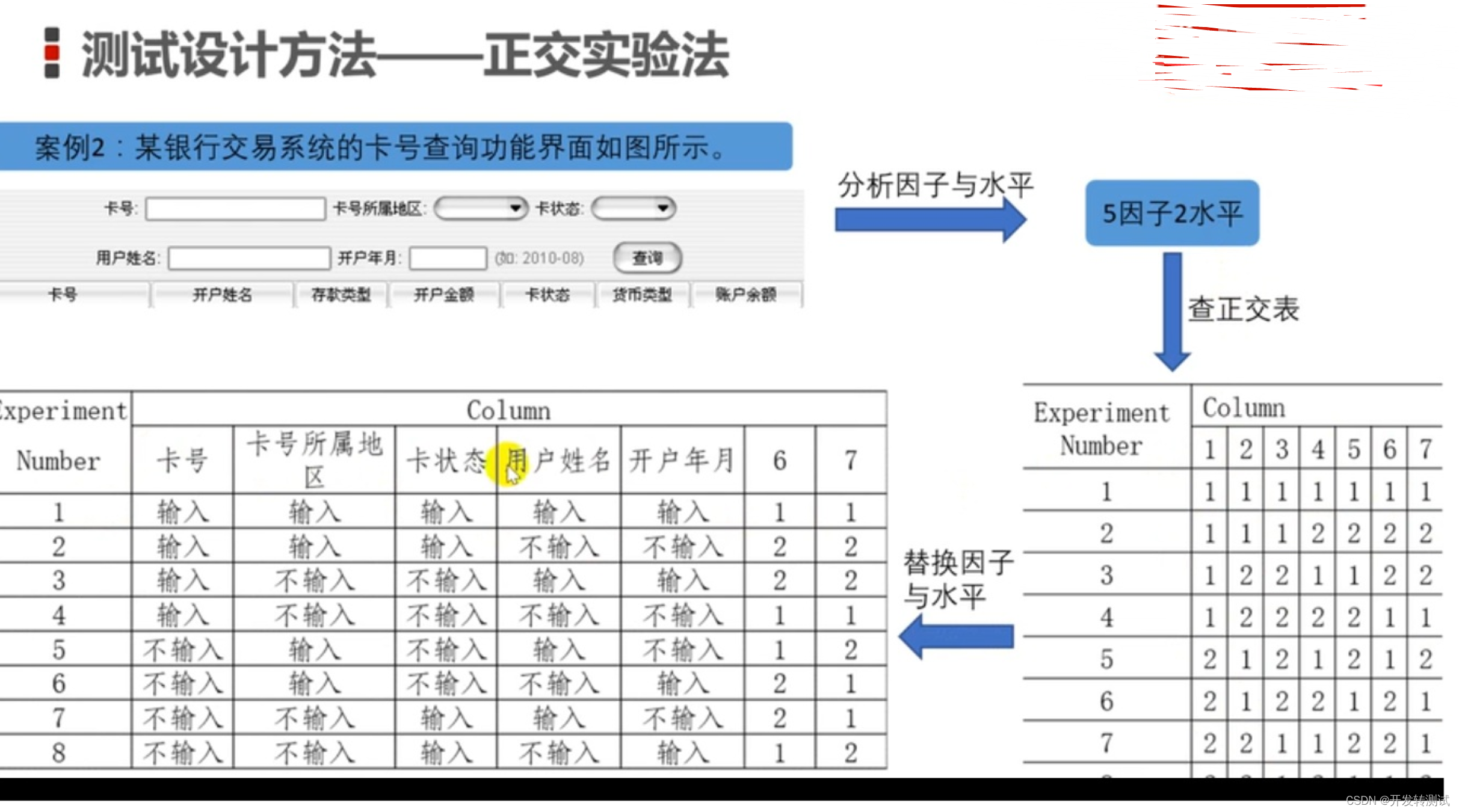
巧计口诀-软件测试的生命周期，黑盒测试设计方法

目录 1。口诀 2。黑盒设计方法适用场合 3。黑盒设计方法详解 3.1。等价类法 3.2。 边界值法 3.3。判定表法 3.4。因果表 3.5。状态迁移图 3.6。场景法 3.7。正交实验法 3.8。错误推断法 1。口诀 又到了找工作的日子&#xff0c;背诵这些基本知识和概念又开始了。我找…...

编程日记 2023/6/6 2:34:08

Android系统的Ashmem匿名共享内存系统分析（1）- Ashmem驱动

声明 其实对于Android系统的Ashmem匿名共享内存系统早就有分析的想法&#xff0c;记得2019年6、7月份Mr.Deng离职期间约定一起对其进行研究的&#xff0c;但因为我个人问题没能实施这个计划&#xff0c;留下些许遗憾…文中参考了很多书籍及博客内容&#xff0c;可能涉及的比较…...

编程日记 2023/6/6 2:29:07

Redis 事务详细介绍

事务 注意&#xff1a;Redis单条命令是保证原子性的&#xff1b;但是事务不保证原子性&#xff01; Redis事务没有隔离级别的概念&#xff0c;所有的命令在事务中&#xff0c;并没有直接被执行&#xff0c;只有发起执行命令时才执行 Redis事务本质&#xff1a;一组命令的集合&…...

编程日记 2023/6/6 2:24:05

2023-5-29第二十九天

consult咨询&#xff0c;查阅&#xff0c;商讨 specialize专门从事&#xff0c;专攻 inspect检查 pattern图案&#xff0c;方式 optimize使最优化 ensemble整体&#xff0c;全体 subscript下标 subscribe签名 sector行业&#xff0c;部门 precedence优先&#xff0c;优…...

编程日记 2023/6/6 2:19:04

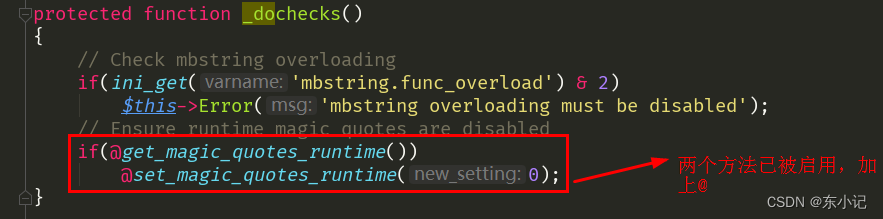
【第三方库】PHP实现创建PDF文件和编辑PDF文件

目录 引入Setasign/fpdf、Setasign/fpdi 解决写入中文时乱码问题 1.下载并放置中文语言包&#xff08;他人封装&#xff09;&#xff1a;https://github.com/DCgithub21/cd_FPDF 2.编写并运行生成字体文件的程序文件&#xff08;addFont.php&#xff09; 中文字体举例&…...

编程日记 2023/6/6 2:14:03

线程的回收及内存演示

ps -elf|grep mthread 查看进程和线程 top -p 6513 查看内存 一、线程的回收 使用pthread_join 函数&#xff1a; #include <pthread.h> int pthread_join(pthread_t thread, void **retval); 注意&#xff1a;pthread_join 是阻塞函数&#xff0c;如果回收的线…...

编程日记 2023/6/6 2:09:02

高精度倾角传感器测量原理

高精度倾角传感器测量原理技术参数 1.性能参数 测量范围&#xff1a;0&#xff5e;30 测量精度&#xff1a;0.06 分 辨 率&#xff1a;0.0001 测量方向&#xff1a;X,Y 时间漂移&#xff1a;0.08/月 更新时间&#xff1a;30ms 上电启动时间&#xff1a;0.5s 2.电…...

编程日记 2023/6/6 2:04:01

Android 12 init流程分析

前言 刚开始接触需要了解的概念理解过程遇到了什么问题代码的位置和流程分析如何分析和调试遇到的问题 基本的概念 .rc 文件 这个文件在Android framework 中服务相关代码可以看到。类似surfaceflinger.rc 、mediaserver.rc等等。 在这些rc里面定义了某一个service&#xff0…...

编程日记 2023/6/6 1:58:59

【Python小技巧】Python操控Chrome浏览器实现网页打开、切换、关闭（送独家Chrome操作打包类源码、Chrome浏览器Cookie在哪里？）

文章目录 前言一、什么时候需要用Python控制浏览器&#xff1f;二、下载Chrome浏览器驱动文件1. 安装Chrome浏览器并查看版本2. 下载浏览器驱动文件3. 解压到python编译器目录&#xff08;python.exe所在目录&#xff09; 三、Python控制Chrome浏览器&#xff08;附源代码&…...

编程日记 2023/6/6 1:53:59

数据在内存中的存储

目录 一、数据类型的介绍 1.C语言基本内置类型 2.类型基本归类 1.整形 2.浮点型 3.构造类型 4.指针类型 二、整形在内存中的存储 三、浮点数在内次中的存储 1.存储形式 2.对M、E的特殊规定 &#xff08;1&#xff09;对M的特殊规定 &#xff08;2&#xff09;对E的…...

编程日记 2023/6/6 1:48:58

Rust in Action笔记 第三章 复合数据类型

通过#[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZI50wIh1-1685693144796)(null)]&#xff09;&#xff0c;不带感叹号的#[allow]仅为下一行代码提供属性&#xff0c;属性有多种分类&#xff0c;文中出现的allow属性称为诊断属性&#xff08;Diag…...

编程日记 2023/6/6 1:43:57

挑战杯推荐项目

“人工智能”创意赛 - 智能艺术创作助手&#xff1a;借助大模型技术&#xff0c;开发能根据用户输入的主题、风格等要求&#xff0c;生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用&#xff0c;帮助艺术家和创意爱好者激发创意、提高创作效率。 ​ - 个性化梦境…...

编程新知 2025/10/8 19:14:30

springboot 百货中心供应链管理系统小程序

一、前言 随着我国经济迅速发展&#xff0c;人们对手机的需求越来越大&#xff0c;各种手机软件也都在被广泛应用&#xff0c;但是对于手机进行数据信息管理&#xff0c;对于手机的各种软件也是备受用户的喜爱&#xff0c;百货中心供应链管理系统被用户普遍使用&#xff0c;为方…...

编程新知 2025/10/22 15:55:37

以下是对华为 HarmonyOS NETX 5属性动画（ArkTS）文档的结构化整理，通过层级标题、表格和代码块提升可读性：

一、属性动画概述NETX 作用&#xff1a;实现组件通用属性的渐变过渡效果&#xff0c;提升用户体验。支持属性&#xff1a;width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项&#xff1a; 布局类属性&#xff08;如宽高&#xff09;变化时&#…...

编程新知 2025/10/26 17:18:45

蓝牙 BLE 扫描面试题大全(2)：进阶面试题与实战演练

前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1)&#xff1a;从基础到实战的深度解析-CSDN博客&#xff0c;但实际面试中&#xff0c;企业更关注候选人对复杂场景的应对能力&#xff08;如多设备并发扫描、低功耗与高发现率的平衡&#xff09;和前沿技术的…...

编程新知 2025/10/27 3:03:38

html-＜abbr＞ 缩写或首字母缩略词

定义与作用 <abbr> 标签用于表示缩写或首字母缩略词&#xff0c;它可以帮助用户更好地理解缩写的含义&#xff0c;尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时&#xff0c;会显示一个提示框。 示例&#x…...

编程新知 2025/9/28 8:06:31

ip子接口配置及删除

配置永久生效的子接口&#xff0c;2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

编程新知 2025/10/26 5:04:25

React---day11

14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store&#xff1a; 我们在使用异步的时候理应是要使用中间件的&#xff0c;但是configureStore 已经自动集成了 redux-thunk&#xff0c;注意action里面要返回函数 import { configureS…...

编程新知 2025/9/13 7:43:29

【Linux手册】探秘系统世界：从用户交互到硬件底层的全链路工作之旅

目录 前言 操作系统与驱动程序 是什么&#xff0c;为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中&#xff0c;我们在使用电子设备时&#xff0c;我们所输入执行的每一条指令最终大多都会作用到硬件上&#xff0c;比如下载一款软件最终会下载到硬盘上&am…...

编程新知 2025/10/24 23:54:13

消息队列系统设计与实践全解析

文章目录 &#x1f680; 消息队列系统设计与实践全解析&#x1f50d; 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡&#x1f4a1; 权衡决策框架 1.3 运维复杂度评估&#x1f527; 运维成本降低策略 &#x1f3d7;️ 二、典型架构设计2.1 分布式事务最终一致…...

编程新知 2025/10/21 0:40:24

热烈祝贺埃文科技正式加入可信数据空间发展联盟

2025年4月29日&#xff0c;在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上&#xff0c;可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞&#xff0c;强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

编程新知 2025/10/20 10:36:10