二叉树part6 | ● 654.最大二叉树 ● 617.合并二叉树 ● 700.二叉搜索树中的搜索 ● 98.验证二叉搜索树
文章目录
- 654.最大二叉树
- 思路
- 代码
- 617.合并二叉树
- 思路
- 代码
- 700.二叉搜索树中的搜索
- 思路
- 代码
- 98.验证二叉搜索树
- 思路
- 官方题解
- 代码
- 困难
- 今日收获
654.最大二叉树
思路
前序遍历构造二叉树。
找出数组中最大值,然后递归处理左右子数组。
时间复杂度On2
空间复杂度On
代码
func constructMaximumBinaryTree(nums []int) *TreeNode {imap:=make(map[int]int)for k,v:=range nums{imap[v]=k}res:=&TreeNode{}var build func(node *TreeNode,l,r int)build = func(node *TreeNode,l,r int){root:=max(nums[l:r+1])index:=imap[root]node.Val=rootif index>l{node.Left=&TreeNode{}build(node.Left,l,index-1)}if index<r{node.Right=&TreeNode{}build(node.Right,index+1,r)}}build(res,0,len(nums)-1)return res
}func max(s []int)int{res:=0for i:=0;i<len(s);i++{if res<s[i]{res=s[i]}}return res
}
617.合并二叉树
思路
递归构建。
目的是合并ab树,每一步递归要做的事当前节点的值为a树和b树相加,左子树为a树左子树和b树左子树递归合并,右子树为a树右子树和b树右子树递归合并。
时间复杂度On
空间复杂度On
代码
func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {res:=&TreeNode{}if root1==nil&&root2==nil{return nil}if root1!=nil&&root2!=nil{res.Val=root1.Val+root2.Valres.Left=mergeTrees(root1.Left,root2.Left)res.Right=mergeTrees(root1.Right,root2.Right)}else if root1!=nil{res.Val=root1.Valres.Left=mergeTrees(root1.Left,nil)res.Right=mergeTrees(root1.Right,nil)}else if root2!=nil{res.Val=root2.Valres.Right=mergeTrees(nil,root2.Right)res.Left=mergeTrees(nil,root2.Left)}return res
}
700.二叉搜索树中的搜索
思路
二叉搜索树中序遍历迭代即可
时间复杂度On
代码
func searchBST(root *TreeNode, val int) *TreeNode {stack:=[]*TreeNode{}cur:=rootfor cur!=nil||len(stack)>0{for cur!=nil{stack=append(stack,cur)cur=cur.Left}cur=stack[len(stack)-1]if cur.Val==val{return cur}stack=stack[:len(stack)-1]cur=cur.Right}return nil
}
98.验证二叉搜索树
思路
递归,每一层递归的目的是判断当前节点的左右子树的所有节点是否都小于或大于当前节点,然后再递归地判断左右子树是否是二叉搜索树。
时间复杂度Onlogn
还可以优化
官方题解
要知道中序遍历下,输出的二叉搜索树节点的数值是有序序列。
有了这个特性,验证二叉搜索树,就相当于变成了判断一个序列是不是递增的了。
时间复杂度On
代码
func isValidBST(root *TreeNode) bool {if root==nil{return true}if root.Left!=nil{ml,_:=maxmin(root.Left)if ml>=root.Val{return false}}if root.Right!=nil{_,mr:=maxmin(root.Right)if mr<=root.Val{return false}}return isValidBST(root.Left)&&isValidBST(root.Right)
}func maxmin(root *TreeNode) (int,int){max,min:=root.Val,root.Valif root.Left!=nil{maxl,minl:=maxmin(root.Left)if max<maxl{max=maxl}if min>minl{min=minl}}if root.Right!=nil{maxr,minr:=maxmin(root.Right)if max<maxr{max=maxr}if min>minr{min=minr}}return max,min
}
困难
开始递归的条件和者终止条件要保持一致性,比如默认只有节点不为空才开始递归,那么终止条件就可以不写节点为空。
今日收获
根据数组构建二叉树的统一写法。
res:=&TreeNode{}
res.Val=…
res.Left=递归…
验证二叉搜索树的写法。
相关文章:

二叉树part6 | ● 654.最大二叉树 ● 617.合并二叉树 ● 700.二叉搜索树中的搜索 ● 98.验证二叉搜索树
文章目录 654.最大二叉树思路代码 617.合并二叉树思路代码 700.二叉搜索树中的搜索思路代码 98.验证二叉搜索树思路官方题解代码困难 今日收获 654.最大二叉树 思路 前序遍历构造二叉树。 找出数组中最大值,然后递归处理左右子数组。 时间复杂度On2 空间复杂度On …...

Linux命令记录
Shells 查看当前系统shell cat /etc/shells # 输出 # /etc/shells: valid login shells /bin/sh /bin/bash /usr/bin/bash /bin/rbash /usr/bin/rbash /bin/dash /usr/bin/dash查看正在使用的shell echo $SHELL # 输出 /bin/bashLinux文件结构 bin:系统可执行文件b…...

eBPF 入门实践教程十五:使用 USDT 捕获用户态 Java GC 事件耗时
eBPF (扩展的伯克利数据包过滤器) 是一项强大的网络和性能分析工具,被广泛应用在 Linux 内核上。eBPF 使得开发者能够动态地加载、更新和运行用户定义的代码,而无需重启内核或更改内核源代码。这个特性使得 eBPF 能够提供极高的灵活性和性能,…...

Linux :: vim 编辑器的初次体验:三种 vim 常用模式 及 使用:打开编辑、退出保存关闭vim
前言:本篇是 Linux 基本操作篇章的内容! 笔者使用的环境是基于腾讯云服务器:CentOS 7.6 64bit。 学习集: C 入门到入土!!!学习合集Linux 从命令到网络再到内核!学习合集 目录索引&am…...

Linux内核进程创建流程
本文代码基于Linux5.10 内容主要参考《Linux内核深度解析》余华兵 当Linux内核要创建一个新进程时, 流程大致如下 ret fork(); if (ret 0) {/* 子进程装载程序 */ret execve(filename, argv, envp); } else if (ret > 0) {/* 父进程 */ } 大致可以分为创建新…...

【03.04】大数据教程--HTTP协议和静态Web服务器
HTTP协议和静态Web服务器 HTTP(Hypertext Transfer Protocol)是一种用于传输超文本的协议,它是Web上的基础通信协议。静态Web服务器是指能够提供静态内容(如HTML、CSS、JavaScript和图像文件)的服务器。 在本教程中&am…...

数据共享传输:台式机和笔记本同步文件!
为什么要在台式机和笔记本同步文件? “我想在台式机和笔记本同步文件。因为我工作时使用笔记本,在家里使用安装了Windows 10系统的台式机,我想要在笔记本和台式机之间同步应用程序、游戏、文档等。有没有一种可以在台式机和笔记本同步文件的…...

java设计模式(十二)代理模式
目录 定义模式结构角色职责代码实现静态代理动态代理jdk动态代理cglib代理 适用场景优缺点 定义 代理模式给某一个对象提供一个代理对象,并由代理对象控制对原对象的引用。说简单点,代理模式就是设置一个中间代理来控制访问原目标对象,以达到…...

Umi微前端水印踩坑以及解决方案
最近公司需要在管理后台加一个水印方案~ 项目用的umi方案,以为就是改一个配置的问题,后来发现坑点还蛮多~ 希望此稳定能帮助到用umi 的你们. 一. 先来说说心路历程 坑点1 umi的水印适配只能在layout中进行配置,也就是路由配置中layout为false的页面无法配置水印,比如说登录页…...

Android RK3588-12 hdmi-in Camera方式支持NV24格式
hdmi-in Camera方式支持NV24格式 modified: hardware/interfaces/camera/device/3.4/default/ExternalCameraDevice.cpp modified: hardware/interfaces/camera/device/3.4/default/ExternalCameraDeviceSession.cpp diff --git a/hardware/interfaces/camera/device/3.4…...

Hive窗口函数详细介绍
文章目录 Hive窗口函数概述样本数据表结构表数据 窗口函数窗口聚合函数count()SQL演示 sum()SQL演示 avg()SQL演示 min()SQL演示 max()SQL演示 窗口分析函数first_value() 取开窗第一个值应用场景SQL演示 last_value()取开窗最后一个值应用场景SQL演示 lag(col, n, default_val…...

牛客网【c语言练习】
单选题 下面代码段的输出是(-12 ) int main() {int a3; printf("%d\n",(aa-a*a)); } aa-9,此时还是等于3,因为a*a只是运算,并没有赋值;之后再算a-9,运算之前a等于3,运算…...

C++类和对象(上)
文章目录 🦍1. 面向过程和面向对象🦧2. 类的引入🐶3. 类的定义🦮4. 类的访问控制和封装🍖4.1 访问限定符🍖4.2 封装 🐩5. 类的作用域🐅6. 类的实例化🐄7. 类的大小计算&a…...
JavaScript 数据透视表 DHTMLX Pivot Crack
DHTMLX Pivot JavaScript 数据透视表 - 强大的数据汇总和报告 使用我们的高速 JavaScript/HTML5 Pivot 组件可视化您的复杂数据,从而提高您的商业智能。 它可以帮助您以方便的方式汇总大型数据集。 主要特征 纯 JavaScript 库,可轻松与任何服务器端集成…...

QT链接库设置
以windows 平台为例,在.pro 文件中: 1 增加 INCLUDEPATH <头文件路径> DEPENDPATH <头文件路径> 2 LIBS -L<库目录路径> -l<库得名字> 3 设置MT、MTD、MD、MDD运行时库 win32:CONFIG(debug, debug|release): { QMAKE_CFLAGS_…...

零点起飞学Android——期末考试课本复习重点
目录 第一章 认识Android第二章 Android常见界面布局第三章 Android常用基本控件第四章 Android 高级控件第五章 Android菜单和对话框 第一章 认识Android 1. Android 界面设计被称为______。 答案:布局 2. Android中常见的布局包括______、______ 、______ 、____…...
Redis为什么快?
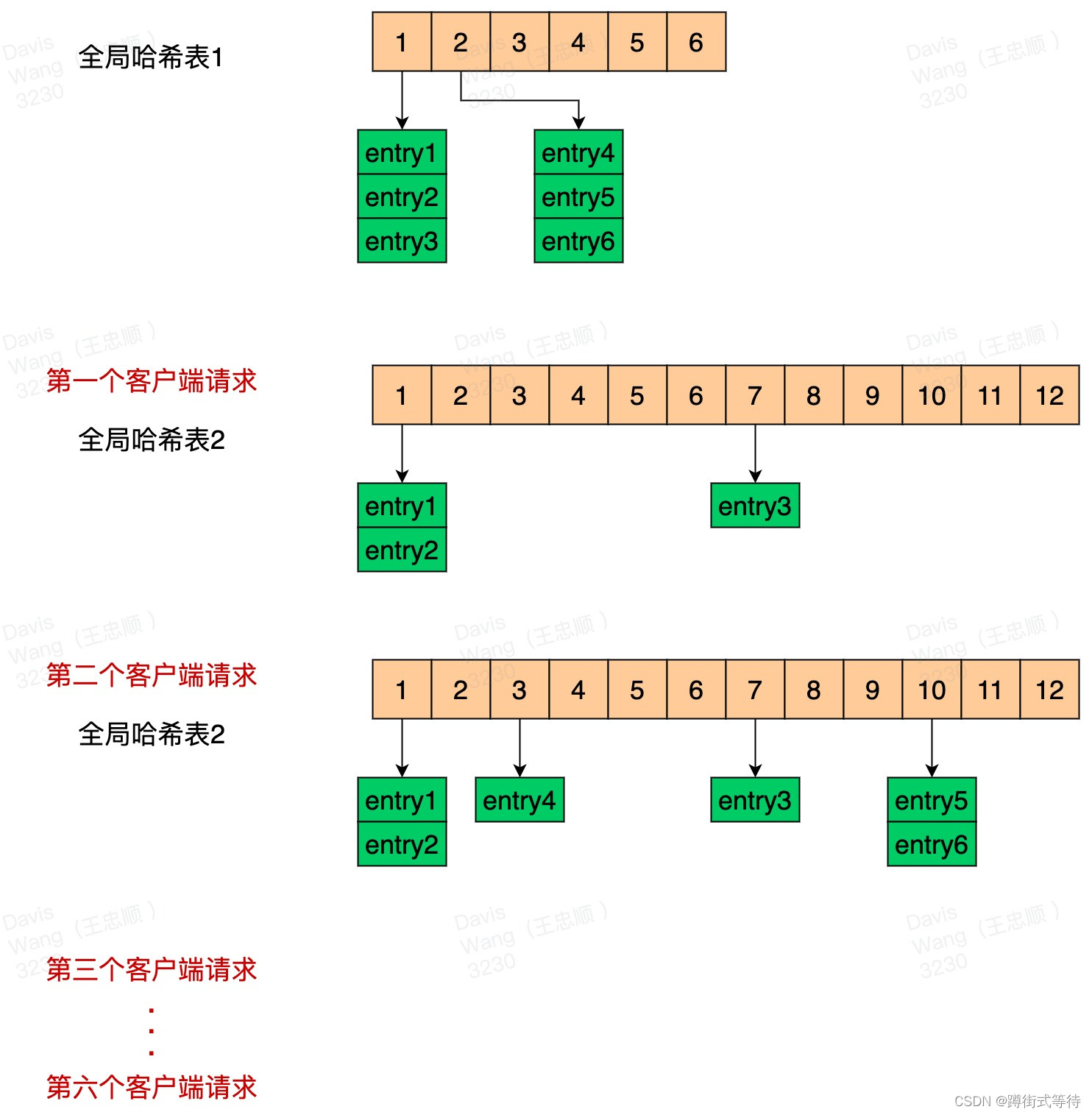
目录 Redis为什么快?渐进式ReHash全局哈希表渐进式ReHash 缓存时间戳 Redis为什么快? 纯内存访问; 单线程避免上下文切换; 渐进式ReHash、缓存时间戳; 前面两个都比较好理解,下面我们主要来说下 渐进式…...
Zabbix从入门到精通以及案例实操系列
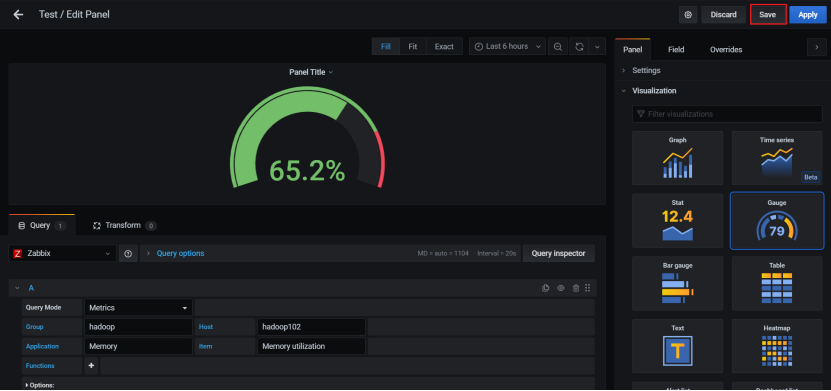
1、Zabbix入门 1.1、Zabbix概述 Zabbix是一款能够监控各种网络参数以及服务器健康性和完整性的软件。Zabbix使用灵活的通知机制,允许用户为几乎任何事件配置基于邮件的告警。这样可以快速反馈服务器的问题。基于已存储的数据,Zabbix提供了出色的报告和…...

水声声波频率如何划分?水声功率放大器可将频率放大到20MHz吗?
水声声波频率如何划分?水声功率放大器可将频率放大到20MHz吗? 现如今我们可以在地球任意地区实现通信,是因为电磁波的作用。但是我们都知道海洋占了全球十分之七面积,电磁波在水下衰减速度太快,无法做到远距离传输&am…...

网络攻防技术--论文阅读--《基于自动数据分割和注意力LSTM-CNN的准周期时间序列异常检测》
英文题目:Anomaly Detection in Quasi-Periodic Time Series based on Automatic Data Segmentation and Attentional LSTM-CNN 论文地址:Anomaly Detection in Quasi-Periodic Time Series Based on Automatic Data Segmentation and Attentional LST…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
