Python3数据分析与挖掘建模(6)离散分布分析示例
1. 离散分布分析示例
相关库:
pandas详细用法
numpy详细用法
1.1 引入算法库
# 引入 pandas库
import pandas as pd # 引入 numpy库
import numpy as np# 读取数据
df=pd.read_csv("data/HR.csv")# 查看数据
df
Out[6]: satisfaction_level last_evaluation ... department salary
0 0.38 0.53 ... sales low
1 0.80 0.86 ... sales medium
2 0.11 0.88 ... sales medium
3 0.72 0.87 ... sales low
4 0.37 0.52 ... sales low... ... ... ... ...
14997 0.11 0.96 ... support low
14998 0.37 0.52 ... support low
14999 NaN 0.52 ... support low
15000 NaN 999999.00 ... sale low
15001 0.70 0.40 ... sale nme
[15002 rows x 10 columns]1.2 Satisfaction Level的分析
(1)分析满意度
过滤异常值
# 创建新变量
[15002 rows x 10 columns]
sl_s=df["satisfaction_level"]# 判断是否有异常值
sl_s.isnull()
Out[8]:
0 False
1 False
2 False
3 False
4 False...
14997 False
14998 False
14999 True
15000 True
15001 False
Name: satisfaction_level, Length: 15002, dtype: bool# 查询异常值
sl_s[sl_s.isnull()]
Out[9]:
14999 NaN
15000 NaN
Name: satisfaction_level, dtype: float64# 列出异常值信息
df[df["satisfaction_level"].isnull()]
Out[10]: satisfaction_level last_evaluation ... department salary
14999 NaN 0.52 ... support low
15000 NaN 999999.00 ... sale low
[2 rows x 10 columns]# 丢弃异常值
sl_s=sl_s.dropna()# 再次查看是否有异常值
sl_s.isnull()
Out[12]:
0 False
1 False
2 False
3 False
4 False...
14995 False
14996 False
14997 False
14998 False
15001 False
Name: satisfaction_level, Length: 15000, dtype: bool
# 都是False,没有问题
基础分析:
# 均值
sl_s.mean()
Out[13]: 0.6128393333333333# 最大值
sl_s.max()
Out[14]: 1.0# 最小值
sl_s.min()
Out[15]: 0.09# 中位数
sl_s.median()
Out[16]: 0.64# 分位数
sl_s.quantile(q=0.25)
Out[17]: 0.44# 分位数
sl_s.quantile(q=0.75)
Out[18]: 0.82# 偏度
sl_s.skew()
Out[19]: -0.47643761717258093# 峰度
sl_s.kurt()
Out[20]: -0.6706959323886252离散化分布分析:
np.histogram(sl_s.values,bins=np.arange(0.0, 1.1, 0.1))
Out[21]:
(array([ 195, 1214, 532, 974, 1668, 2146, 1973, 2074, 2220, 2004],dtype=int64),array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ]))上述代码,使用了NumPy的np.histogram()函数来计算数据的直方图。
具体而言,np.histogram(sl_s.values, bins=np.arange(0.0, 1.1, 0.1))的含义是:
sl_s.values是一个Series对象,表示满意度(satisfaction_level)的数据。np.arange(0.0, 1.1, 0.1)用于指定直方图的边界范围,从0.0到1.0,步长为0.1。np.histogram()函数将根据指定的边界范围对数据进行分组,并返回每个分组中数据的频数和边界值。
输出结果中的第一个数组表示每个分组中数据的频数,第二个数组表示分组的边界值。
在这个例子中,结果显示了从0.0到1.0的10个分组,并给出了每个分组的频数。例如,频数为195的分组包含了满意度在0.0到0.1之间的数据。
这样的直方图可以帮助我们了解满意度数据的分布情况,以及各个区间内的数据数量。
1.3 LastEvaluation的分析
le_s=df["last_evaluation"]le_s[le_s.isnull()]
Out[25]: Series([], Name: last_evaluation, dtype: float64) # 没有异常的值le_s.mean()
Out[26]: 67.37373216904412 # le_s.max()
Out[28]: 999999.0 # 最大值过大,可能有问题le_s.min()
Out[29]: 0.36 # 最小值太小,可能有问题le_s.median()
Out[30]: 0.72 # 当前中位数正常le_s.std()
Out[31]: 8164.407523745649le_s.skew()
Out[32]: 122.48265175204614 # 偏度,说明均值比大部分值都大很多le_s.kurt()
Out[33]: 15001.999986807796 # 峰度,说明该分布形变非常大# 获取大于1的值
le_s[le_s>1]
Out[34]:
15000 999999.0 # 只有这个值大于1,说明这个值有问题,需要抛弃掉
Name: last_evaluation, dtype: float64 # 偏离太多的异常值,会对均值和方差造成影响# 过滤异常值
le_s=le_s[le_s<=1]
le_s[le_s>1]
Out[36]: Series([], Name: last_evaluation, dtype: float64)提取正常值信息
le_s=df["last_evaluation"]
q_low=le_s.quantile(q=0.25)
q_high=le_s.quantile(q=0.75)
q_interval=q_high-q_low
k=1.5
le_s=le_s[le_s<q_high+k*q_interval][le_s>q_low-k*q_interval]
le_s
Out[49]:
0 0.53
1 0.86
2 0.88
3 0.87
4 0.52...
14996 0.53
14997 0.96
14998 0.52
14999 0.52
15001 0.40
Name: last_evaluation, Length: 15001, dtype: float64# 获取数量
len(le_s)
Out[50]: 15001# 获取分布图
np.histogram(le_s.values,bins=np.arange(0.0, 1.1, 0.1))
Out[51]:
(array([ 0, 0, 0, 179, 1390, 3396, 2234, 2062, 2752, 2988],dtype=int64),array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ]))去掉异常值后重新计算
le_s.max()
Out[52]: 1.0 # 正常,在0~1区域内le_s.min()
Out[53]: 0.36 # 正常,在0~1区域内le_s.mean()
Out[54]: 0.7160675954936337 # 均值不是太大le_s.median()
Out[55]: 0.72 # 中位数不是太大,且接近均值,说明差异性低le_s.std()
Out[56]: 0.17118464250786233 le_s.skew()
Out[57]: -0.02653253746872579 # 偏度小于0,没有异常le_s.kurt()
Out[58]: -1.2390454655108427 # 峰度小于0,没有异常1.4 NumberProject的分析
静态结构分析:
np_s=df["number_project"]
np_s[np_s.isnull()]
Out[60]: Series([], Name: number_project, dtype: int64)np_s.mean()
Out[61]: 3.8026929742700974np_s.std()
Out[62]: 1.232732779200601np_s.median()
Out[63]: 4.0np_s.max()
Out[64]: 7np_s.min()
Out[65]: 2np_s.skew()
Out[66]: 0.3377744235231047np_s.kurt()
Out[67]: -0.49580962709450604np_s.value_counts()
Out[68]:
number_project
4 4365
3 4055
5 2761
2 2391
6 1174
7 256
Name: count, dtype: int64np_s.value_counts(normalize=True)
Out[70]:
number_project
4 0.290961
3 0.270297
5 0.184042
2 0.159379
6 0.078256
7 0.017064
Name: proportion, dtype: float64np_s.value_counts(normalize=True).sort_index()
Out[71]:
number_project
2 0.159379
3 0.270297
4 0.290961
5 0.184042
6 0.078256
7 0.017064
Name: proportion, dtype: float64
在上述分析代码中,静态结构分析的内容主要体现在对"number_project"列数据的描述统计部分,包括以下代码段:
np_s.mean() # 平均值
np_s.std() # 标准差
np_s.median() # 中位数
np_s.max() # 最大值
np_s.min() # 最小值
np_s.skew() # 偏度
np_s.kurt() # 峰度
np_s.value_counts() # 频数统计
np_s.value_counts(normalize=True) # 频率统计
np_s.value_counts(normalize=True).sort_index() # 按索引排序的频率统计
这些统计指标可以帮助我们了解"number_project"列数据的分布和特征,从而进行静态结构分析。例如,通过计算平均值、标准差、偏度和峰度等指标,你可以了解该列数据的集中趋势、离中趋势、偏态和峰态情况。而频数统计和频率统计可以提供不同取值的出现次数和占比,进一步展示数据的分布情况。
1.5 AverageMonthlyHours的分析
amh_s=df["average_monthly_hours"]
amh_s.mean()
Out[75]: 201.0417277696307 # 均值比较高amh_s.std()
Out[76]: 49.94181527437925 # 标准差,比较正常amh_s.max()
Out[77]: 310amh_s.min()
Out[78]: 96amh_s.skew()
Out[79]: 0.05322458779916304 # 偏度,稍微振偏amh_s.kurt()
Out[80]: -1.1350158577565719 # 峰度,比较平缓# 用异常值公式剔除异常值
amh_s=amh_s[amh_s<amh_s.quantile(0.75)+1.5*(amh_s.quantile(0.75)-amh_s.quantile(0.25))][amh_s>amh_s.quantile(0.25)-1.5*(amh_s.quantile(0.75)-amh_s.quantile(0.25))]len(amh_s)
Out[82]: 15002 # 原数量就是15002,说明没有异常值# 查看分布
np.histogram(amh_s.values, bins=np.arange(amh_s.min(),amh_s.max()+10, 10))
Out[84]:
(array([ 168, 171, 147, 807, 1153, 1234, 1075, 824, 818, 758, 751,738, 856, 824, 987, 1002, 1045, 935, 299, 193, 131, 86],dtype=int64),array([ 96, 106, 116, 126, 136, 146, 156, 166, 176, 186, 196, 206, 216,226, 236, 246, 256, 266, 276, 286, 296, 306, 316], dtype=int64))1.6 TimeSpendCompany的分析
tsc_s=df["time_spend_company"]
tsc_s.value_counts().sort_index()
Out[86]:
time_spend_company
2 3245
3 6445
4 2557
5 1473
6 718
7 188
8 162
10 214
Name: count, dtype: int64
tsc_s.mean()
Out[87]: 3.498066924410079上述数据中,根据sort_index()结果可以得知,没有存在异常数。
1.7 WorkAccident的分析
wa_s=df["Work_accident"]
wa_s.value_counts()
Out[89]: Work_accident
0 12833
1 2169
Name: count, dtype: int64# 均值
wa_s.mean()
Out[90]: 0.14458072257032395 #说明事故率是百分之十四点四1.8 Left的分析
l_s=df["left"]# 分布
l_s.value_counts()
Out[95]:
left
0 11428
1 3574
Name: count, dtype: int64 # 离职率高1.9 PromotionLast5Years的分析
pl5_s=df["promotion_last_5years"]
pl5_s.value_counts()
Out[97]:
promotion_last_5years
0 14683
1 319
Name: count, dtype: int64 # 晋升数为319,说明只有少部分得到晋升 1.10 Salary的分析
s_s=df["salary"]s_s.where(s_s!="nme").dropna().value_counts()
Out[103]:
salary
low 7318
medium 6446
high 1237
Name: count, dtype: int64 # 说明高收入人群是极少数,低收入人群是半数,部分人群中等收入1.11 Department的分析
d_s=df["department"]
d_s.value_counts(normalize=True) # 查询分布比例
Out[105]:
department
sales 0.275963
technical 0.181309
support 0.148647
IT 0.081789
product_mng 0.060125
marketing 0.057192
RandD 0.052460
accounting 0.051127
hr 0.049260
management 0.041994
sale 0.000133
Name: proportion, dtype: float64# 移除异常值
d_s=d_s.where(d_s!="sale").dropna()d_s.value_counts(normalize=True)
Out[108]:
proportion
0.276000 0.1
0.181333 0.1
0.148667 0.1
0.081800 0.1
0.060133 0.1
0.057200 0.1
0.052467 0.1
0.051133 0.1
0.049267 0.1
0.042000 0.1
Name: proportion, dtype: float641.12 简单对比分析操作
(1)对比分析
剔除异常值
# 移除异常值,这里移除的是isNull()查出来的异常值
df=df.dropna(axis=0,how="any")# 移除异常值,这里根据规则,移除不符合规范的值
df=df[df["last_evaluation"]<=1][df["salary"]!="name"][df["department"]!="sale"]# 清洗后的值
df
Out[110]: satisfaction_level last_evaluation ... department salary
0 0.38 0.53 ... sales low
1 0.80 0.86 ... sales medium
2 0.11 0.88 ... sales medium
3 0.72 0.87 ... sales low
4 0.37 0.52 ... sales low... ... ... ... ...
14995 0.37 0.48 ... support low
14996 0.37 0.53 ... support low
14997 0.11 0.96 ... support low
14998 0.37 0.52 ... support low
15001 0.70 0.40 ... sale nme根据部门分组,生成新表
df.loc[:,["satisfaction_level","last_evaluation","number_project","department"]].groupby("department").mean()
Out[131]: satisfaction_level last_evaluation number_project
department
IT 0.618142 0.716830 3.816626
RandD 0.619822 0.712122 3.853875
accounting 0.582151 0.717718 3.825293
hr 0.598809 0.708850 3.654939
management 0.621349 0.724000 3.860317
marketing 0.618601 0.715886 3.687646
product_mng 0.619634 0.714756 3.807095
sales 0.614447 0.709717 3.776329
support 0.618300 0.723109 3.803948
technical 0.607897 0.721099 3.877941
上述数据中,根据 satisfaction_level 的平均值可以看出对HR的满意度是比较低的。其他的数据也可以反映出相应的情况。
脚本解析:
注意,在这个示例中,使用了.loc来选择多个列,并通过列表传递给.groupby()函数。然后,调用.mean()函数来计算平均值。执行该代码将会输出每个部门的各项指标的平均值。相关文章:
离散分布分析示例)
Python3数据分析与挖掘建模(6)离散分布分析示例
1. 离散分布分析示例 相关库: pandas详细用法 numpy详细用法 1.1 引入算法库 # 引入 pandas库 import pandas as pd # 引入 numpy库 import numpy as np# 读取数据 dfpd.read_csv("data/HR.csv")# 查看数据 df Out[6]: satisfaction_level last_eval…...

汇编语言程序设计基础知识二
五、顺序结构 1、程序设计的步骤 1、分析问题 2、建立数据模型 3、设计算法 4、编制程序 5、上机调试 2、流程图的应用 3、程序的基本控制结构 1、顺序结构:程序顺序执行,不发生跳转 2、分支结构:程序在执行过程中发生跳转 3、循环…...

一文详解!Robot Framework Selenium UI自动化测试入门篇
目录 前言: 自动化框架的选择 测试环境的搭建 导入Selenium2Library包 关键字是什么? 创建测试用例 前言: 自动化测试的重要性越来越受到人们的重视,因为它可以提高测试效率、降低测试成本并减少人为错误的出现。为了满足这…...

Java 9 模块化系统详解
Java 9 模块化系统详解 一、简介1. 引入模块化系统原因2. 模块化系统带来的优势和挑战3. 模块化关键概念 二、模块化基础1. 模块化源代码结构规范2. 模块定义与描述符3. 打包可执行模块 三、模块化系统的高级特性1. 模块发现与解决依赖2. 模块化升级与替换3. 模块化动态访问 四…...
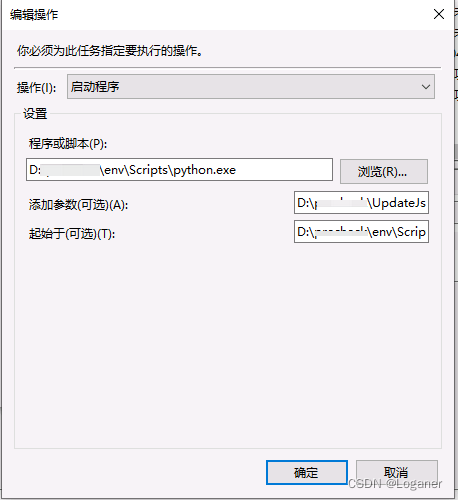
Windows定时执行Python脚本
在Linux环境下我们可以使用crontab工具来定时的执行脚本,可以很轻松的管理各个虚拟环境下的py文件在Windows上可以使用任务计划程序来定时执行我们的脚本 关于这个的基本使用可以查看我前面的博客 https://blog.csdn.net/wyh1618/article/details/125725967?spm10…...

数据科学简介:如何使用 Pandas 库处理 CSV 文件
部分数据来源:ChatGPT 什么是 CSV 文件? CSV ( Comma Separated Values)文件是一种常见的文本文件格式,它通常用于存储结构化数据,因为它可以轻松地转换成电子表格,如Excel。 CSV 文件是以逗号作为分隔符的表格数据。文件中的每行代表一个记录,每列代表一个属性。例如…...
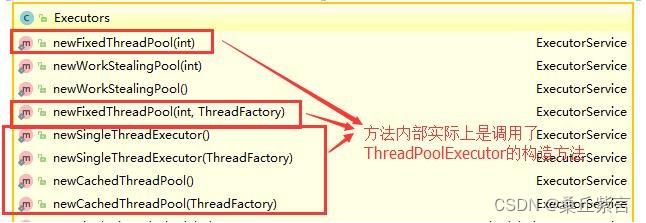
面试专题:java多线程(2)-- 线程池
1.为什么要用线程池? 线程池提供了一种限制和管理资源(包括执行一个任务)。 每个线程池还维护一些基本统计信息,例如已完成任务的数量。 这里借用《Java并发编程的艺术》提到的来说一下使用线程池的好处: 降低资源消…...

Linux文件权限及用户管理
文件权限 在Linux中,每个文件和目录都有一组权限,这些权限决定了哪些用户可以访问文件或目录,以及他们可以进行什么样的操作。权限分为三类: 所有者权限:这些权限适用于文件或目录的所有者。 组权限:这些…...

以AI为灯,照亮医疗放射防护监管盲区
相信绝大部分人都有在医院拍X光片的经历,它能够让医生更方便快速地找出潜在问题,判断病人健康状况,是医疗诊断过程中的常见检查方式。但同时X射线也是一把双刃剑,它的照射量可在体内累积,对人体血液白细胞有杀伤力&…...
:单元测试的基本使用方法)
Golang单元测试详解(一):单元测试的基本使用方法
Golang 单元测试 Golang 中的单元测试是使用标准库 testing 来实现的,编写一个单元测试是很容易的: 创建测试文件:在 Go 项目的源代码目录下创建一个新的文件(和被测代码文件在同一个包),以 _test.go 为后…...

数据库的序列
目录 一、序列是什么 二、序列的用途 二、创建序列 三、查看、修改、删除序列 四、使用序列 (1)在插入语句中使用 (2)不在插入语句中使用 五、使用序列的例子 一、序列是什么 数据库对象分为:用户、视图、索引…...

2022年回顾
年总写完了(已持续多年),顺便写个小的回顾。 寻找属于自己的方向 无论当前干啥,大多数都不是真正适合你的,但是,你又不能不做下去,那么,持续的寻找适合的,就是一种解开…...
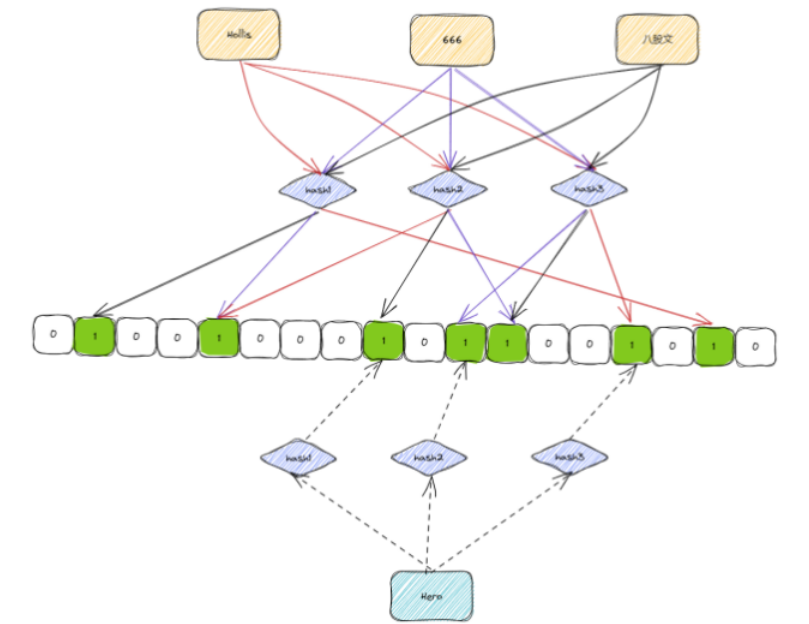
40亿个QQ号,限制1G内存,如何去重?
40亿个unsigned int,如果直接用内存存储的话,需要: 4*4000000000 /1024/1024/1024 14.9G ,考虑到其中有一些重复的话,那1G的空间也基本上是不够用的。 想要实现这个功能,可以借助位图。 使用位图的话&a…...

【django】django的orm的分组查询
前言:django当中分组查询如何实现? annotate from myapp import models from django.db.models.functions import TruncMonth from django.db.models import Count,Avg# 分组 values 就是取值作用 model.Book.objects.values(month).annotate(countCo…...

MySQL5.8在Windows下下载+安装+配置教程
MySQL是一款常用的关系型数据库管理系统,本文将介绍MySQL5.8在Windows下的安装配置教程。 1. 软件下载地址 免安装版下载地址:https://dev.mysql.com/downloads/mysql/安装版下载地址:https://dev.mysql.com/downloads/installer/ 2. 免安…...
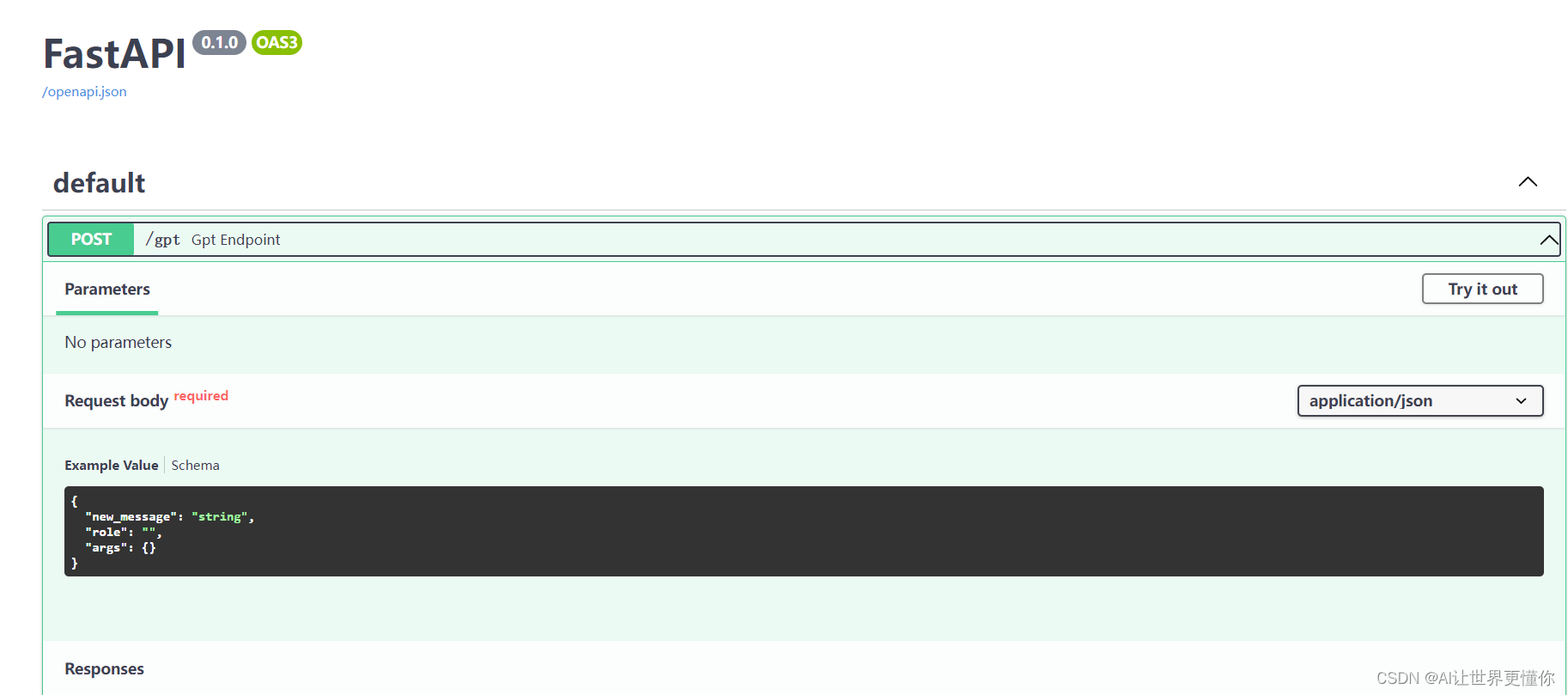
Flask or FastAPI? Python服务端初体验
1. 引言 最近由于工作需要,又去了解了一下简单的python服务搭建的相关工作,主要是为了自己开发的模型或者工具给同组的人使用。之前介绍的针对于数据科学研究比较友好的一个可以展示的前端框架Streamlit可以说是一个利器。不过,随着ChatGPT的…...

《计算机组成原理》唐朔飞 第7章 指令系统 - 学习笔记
写在前面的话:此系列文章为笔者学习计算机组成原理时的个人笔记,分享出来与大家学习交流。使用教材为唐朔飞第3版,笔记目录大体与教材相同。 网课 计算机组成原理(哈工大刘宏伟)135讲(全)高清_…...
Linux:apache网页优化
Linux:apache网页优化 一、Apache 网页优化二、网页压缩2.1 检查是否安装 mod_deflate 模块2.2 如果没有安装mod_deflate 模块,重新编译安装 Apache 添加 mod_deflate 模块2.3 配置 mod_deflate 模块启用2.4 检查安装情况,启动服务2.5 测试 m…...
涨点技巧:注意力机制---Yolov8引入Resnet_CBAM,CBAM升级版
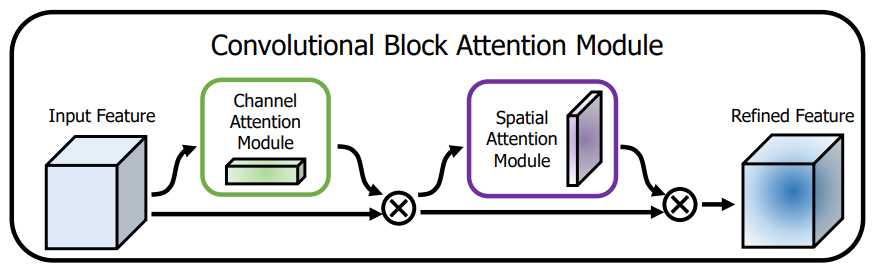
1.计算机视觉中的注意力机制 一般来说,注意力机制通常被分为以下基本四大类: 通道注意力 Channel Attention 空间注意力机制 Spatial Attention 时间注意力机制 Temporal Attention 分支注意力机制 Branch Attention 1.1.CBAM:通道注意力和空间注意力的集成者 轻量级…...

solr教程
一:安装配置 下载完成之后,解压solr文件,解压tomcat 1.1 在tomcat安装solr,并且建立solrCore 把solr5.5目录下的server/solr-webapp/webapp 重命名为solr,并且放置到tomcat/webapp的目录下。 打开tomcat/webapp/solr/WEB-INF/web.xml新建…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...
