常微分方程(ODE)求解方法总结
常微分(ODE)方程求解方法总结
- 1 常微分方程(ODE)介绍
- 1.1 微分方程介绍和分类
- 1.2 常微分方程的非计算机求解方法
- 1.3 线性微分方程求解的推导过程
- 2 一阶常微分方程(ODE)求解方法
- 2.1 欧拉方法
- 2.1.1 欧拉方法
- 2.1.2 欧拉方法的误差分析
- 2.1.3 欧拉方法的改进思路1——添加高阶项
- 2.1.4 欧拉方法的改进思路2——对斜率采用更好的估值方法
- 2.1.4.1 修恩法
- 2.1.4.2 中点方法
- 2.1.5 欧拉方法的改进思路3
- 2.2 龙格-库塔法
1 常微分方程(ODE)介绍
1.1 微分方程介绍和分类
举例:假设跳伞人的下落速度v于时间有如下关系:
d v d t = g − c m v \frac{dv}{dt} = g-\frac{c}{m}v dtdv=g−mcv (1.1)
其中g为重力常数,m为质量,c为阻力系数。
被微分的量v因变量,与v有关的变量t称为自变量。
如果函数只有一个自变量,那么方程就称为常微分方程(ordinary differential equation,ODE)。
如果函数含有两个或者多个自变量,则成为偏微分方程(partialdifferential equation,PDE)。
此外,微分方程也可以根据阶数来分类:最高阶导数是一阶导数,则称为一阶微分方程(first-order-equation);最高阶导数是二阶导数,则称为二阶微分方程(second-order-equation)。例如如(1.1)中就是一阶微分方程,下式(1.2)就是一个二阶微分方程。
m d 2 x d t 2 + c d x d t + k x = 0 m\frac{d^2x}{dt^2} +c\frac{dx}{dt} + kx = 0 mdt2d2x+cdtdx+kx=0 (1.2)
高阶微分方程能简化成一阶方程组。考虑上式(1.2),定义新变量y,令
y = d x d t y=\frac{dx}{dt} y=dtdx (1.3)
对上式取微分得:
d y d t = d 2 x d t 2 \frac{dy}{dt}=\frac{d^2x}{dt^2} dtdy=dt2d2x (1.4)
将式(1.3)和(1.4)代入式(1.2)中得到:
m d y d t + c y + k x = 0 m\frac{dy}{dt} +cy + kx = 0 mdtdy+cy+kx=0 (1.5)
于是原来的二阶微分方程(1.2)可等价于两个一阶方程组(1.3)和(1.5)。
同样的,其他的n阶微分方程也可以用类似的方式简化。
1.2 常微分方程的非计算机求解方法
常微分方程通常采用解析积分得方法来求解。如对于式(1.1),先乘以dt,在进行积分得到:
v = ∫ ( g − c m v ) d t v = \int{(g-\frac{c}{m}v)dt} v=∫(g−mcv)dt (1.6)
对于上式(1.6),是可以精确的推导出该积分得函数表达式的。因为该方程是线性的。
但在实际中,很多方程(是非线性的)精确解是无法求出的。于是提出了一个方法,就是将方程线性化。
( n n n阶)线性常微分方程的一般形式是:
a n ( x ) y ( n ) + . . . + a 2 ( x ) y ( 2 ) + a 1 ( x ) y ′ + + a 0 ( x ) y = f ( x ) a_n(x)y^{(n)}+...+a_2(x)y^{(2)}+a_1(x)y'++a_0(x)y = f(x) an(x)y(n)+...+a2(x)y(2)+a1(x)y′++a0(x)y=f(x) (1.7)
其中, y ( n ) y^{(n)} y(n)是y关于x的n阶导数, a n ( x ) a_n(x) an(x)和 f ( x ) f(x) f(x)都是关于x的函数。因为该方程中未出现因变量y与其导数的乘积,也没有出现非线性函数。所以认为它是线性的。
如下式(1.8)是一个非线性微分方程:
d 2 x d t 2 + g l s i n ( x ) = 0 \frac{d^2x}{dt^2} +\frac{g}{l} sin(x)= 0 dt2d2x+lgsin(x)=0 (1.8)
由于含有 s i n ( x ) sin(x) sin(x)为非线性函数,故该微分方程是非线性的。
线性常微分方程是可以通过解析法求解的。但是,大部分非线性方程无法精确求解。
1.3 线性微分方程求解的推导过程
拿一个简单的方程举例。首先给定函数:
y = − 0.5 x 4 + 4 x 3 − 10 x 2 + 8.5 x + 1 y=-0.5x^4+4x^3-10x^2+8.5x+1 y=−0.5x4+4x3−10x2+8.5x+1 (1.9)
这是一个四次多项式。对其进行微分,就得到一个常微分方程:
d y d x = − 2 x 3 + 12 x 2 − 20 x + 8.5 \frac{dy}{dx}=-2x^3+12x^2-20x+8.5 dxdy=−2x3+12x2−20x+8.5 (1.10)
对式(1.10)乘以dx,在进行积分得到:
y = ∫ ( − 2 x 3 + 12 x 2 − 20 x + 8.5 ) d x y=\int{(-2x^3+12x^2-20x+8.5)}dx y=∫(−2x3+12x2−20x+8.5)dx (1.11)
应用积分法则得出解为:
y = − 0.5 x 4 + 4 x 3 − 10 x 2 + 8.5 x + C y=-0.5x^4+4x^3-10x^2+8.5x+C y=−0.5x4+4x3−10x2+8.5x+C (1.12)
除了相差一个C外,其余都与原函数相同。这个C称为积分常数(constant of integration)。
出现一个任意常数C表明,积分的结果并不算是唯一的。无限多个常数C对应无限多个可能的函数,都满足微分方程。下图给出了6个满足条件的函数:
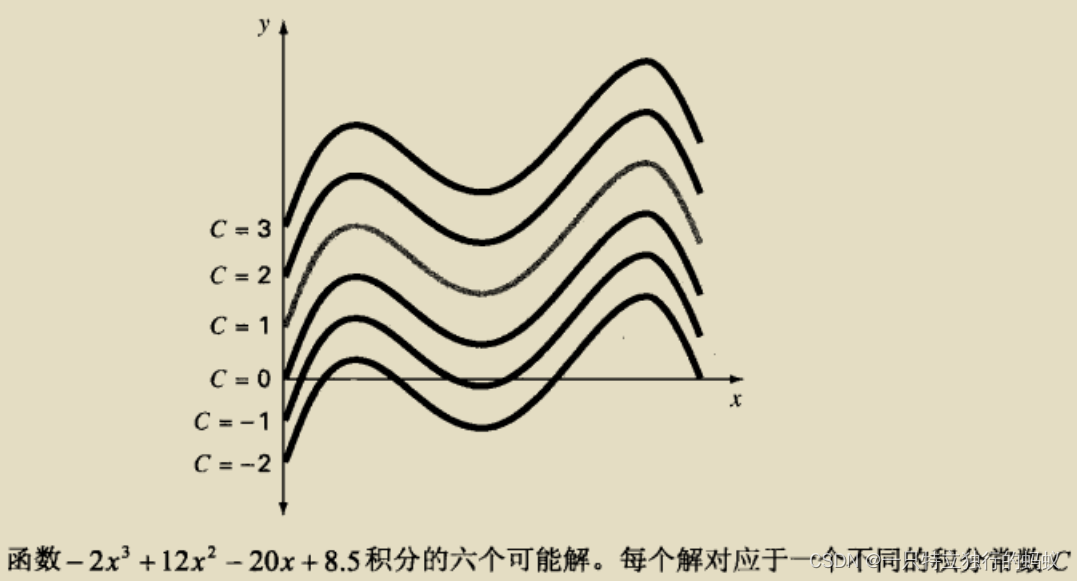
为了将解完全确定下来,微分方程通常伴随有辅助条件(auxiliary conditions)。对于一阶常微分方程,有一类被称为**初值(initial value)**的辅助条件,这类条件用于确定常数值,从而使得解是唯一的。例如,给式(1.11)添加初始条件x=0,y=1。带入式(1.12)中,可推导出C=1。于是就得到了唯一解:
y = − 0.5 x 4 + 4 x 3 − 10 x 2 + 8.5 x + 1 y=-0.5x^4+4x^3-10x^2+8.5x+1 y=−0.5x4+4x3−10x2+8.5x+1
这个解同时满足常微分方程和指定的初始条件。
当处理n阶微分方程时,就需要n个条件来确定唯一解。如果所有的条件都是在自变量同一值处指定的,那么问题就称为初值问题(initial-value problem)。与之相对的,边值问题(boundary-value problems),就是指在自变量的不同值处指定初始条件。
2 一阶常微分方程(ODE)求解方法
2.1 欧拉方法
2.1.1 欧拉方法
还是拿式(1.1)举例:
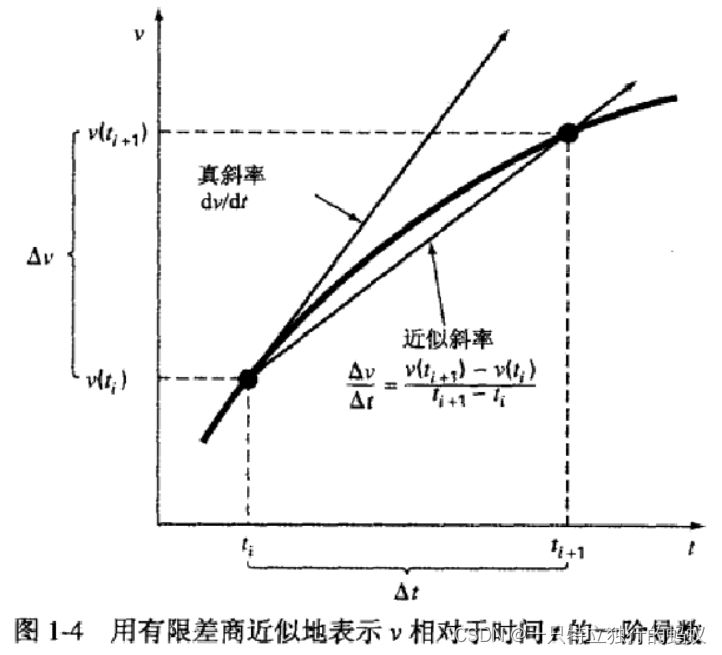
d v d t ≈ Δ v Δ t = v ( t i + 1 ) − v ( t i ) t i + 1 − t i \frac{dv}{dt} \approx \frac{\Delta v}{\Delta t} = \frac{v(t_{i+1}) - v(t_{i})}{t_{i+1} - t_{i}} dtdv≈ΔtΔv=ti+1−tiv(ti+1)−v(ti) (2.1)
其中, Δ v \Delta v Δv和 Δ t \Delta t Δt分别为速度与时间的差分, v ( t i ) v(t_{i}) v(ti)为初始时刻 t i t_i ti的速度, v ( t i + 1 ) v(t_{i+1}) v(ti+1)为下一个时刻 t i + 1 t_{i+1} ti+1的速度。注意, d v d t ≈ Δ v Δ t \frac{dv}{dt} \approx \frac{\Delta v}{\Delta t} dtdv≈ΔtΔv 是一个近似计算,因为:
d v d t = lim Δ t → 0 Δ v Δ t \frac{dv}{dt} = \lim_{\Delta t \to 0}\frac{\Delta v}{\Delta t} dtdv=limΔt→0ΔtΔv
式(2.1)称为在时刻 t i t_i ti处导数的有限差商(finite divided difference)逼近。将其代入式(1.1)中可得:
d v d t ≈ v ( t i + 1 ) − v ( t i ) t i + 1 − t i = g − c m v ( t i ) \frac{dv}{dt} \approx\frac{v(t_{i+1}) - v(t_{i})}{t_{i+1} - t_{i}} = g-\frac{c}{m}v(t_i) dtdv≈ti+1−tiv(ti+1)−v(ti)=g−mcv(ti) (2.2)
对该方程进行整理可得:
v ( t i + 1 ) = v ( t i ) + [ g − c m v ( t i ) ] ( t i + 1 − t i ) v(t_{i+1}) = v(t_{i}) + [g-\frac{c}{m}v(t_i)](t_{i+1} - t_{i}) v(ti+1)=v(ti)+[g−mcv(ti)](ti+1−ti) (2.3)
注意1:在式(2.3)的中括号内部分 g − c m v ( t i ) g-\frac{c}{m}v(t_i) g−mcv(ti)其实就是式(1.1)常微分方程的右边 g − c m v g-\frac{c}{m}v g−mcv,是不过这个是一个估计值,是拿 t i t_i ti对刻的速度来估计 t i t_i ti ~ t i + 1 t_{i+1} ti+1这段时间的速度,但只要两个时间点距离越近,这个估值就准确。
根据式(2.3),如果给定了在某一对刻 t i t_i ti的初始值速度 v i v_i vi,就很容易计算出下一时刻 t i + 1 t_{i+1} ti+1的速度 v i + 1 v_{i+1} vi+1。接着又可以用 t i + 1 t_{i+1} ti+1时刻的新速度值来计算 t i + 2 t_{i+2} ti+2的速度,然后依次继续下去。这样,用这种方式就可以计算出任意时刻的速度。
新值 = 旧值 + 斜率 × 步长 新值 = 旧值 + 斜率 \times 步长 新值=旧值+斜率×步长
用数学语言表述为:
v i + 1 = v i + ϕ × h v_{i+1} = v_{i} + \phi \times h vi+1=vi+ϕ×h(2.4)
这种方法的就命名为欧拉法(Euler’s method)(或欧拉一柯西法(Euler-Cauchy method),或折线法
(point-slope method)。
欧拉方法利用斜率(等于一阶导数在 x i x_i xi处的值),通过线性外推的办法预测出y在前进步长h之后 x i + 1 x_{i+1} xi+1处的新值:
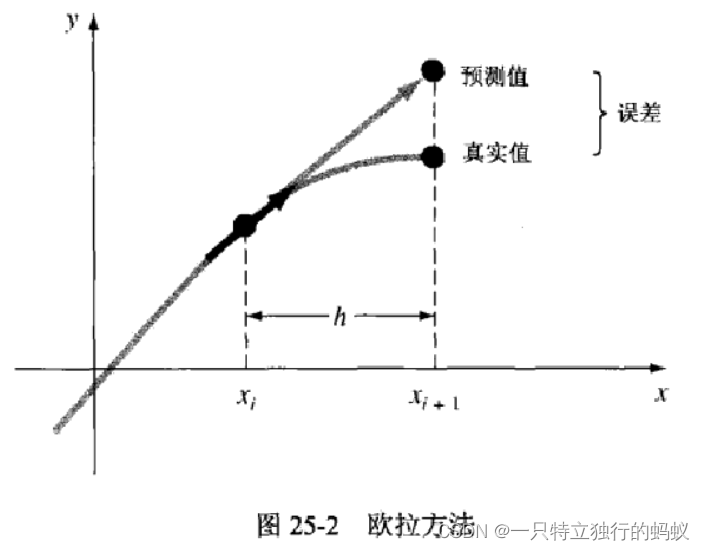
利用上面的方法,取步长为2(也就是每隔2秒,计算一次速度值),于是得到一系列时间t与速度v的值,将这些计算结果与精确解同时画在一个图中:
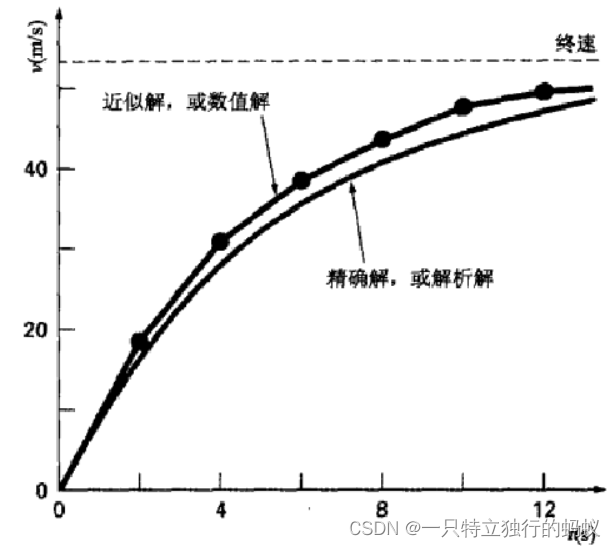
图5 速度v与时间t的关系的常微分方程的数值解与解析解的对比
上图中,如果我们将步长减小一半,以1秒的步长计算得到的结果,其误差将会更小,从而直线段的轨迹更趋近于真实解。但是步长每减小一半,可以得到更精确的结果,所需要的计算量也会翻一番。
2.1.2 欧拉方法的误差分析
常微分方程数值解的误差包括两种类型:
(1)截断(Truncation)误差或离散误差,是由逼近Y值的方法本身引起的。
(2)舍入(Round-off误差,是由于计算机能保留的有效数字有限而引起的。
截断误差由两部分组成:第一部分是局部截断误差(local truncation error),指方法在一步迭代中所产生的误差。第二部分是传播截断误差(propagated truncation error),它是由前面各步中产生的逼近值引起的,这两部分的和称为整体截断误差或全局截断误差(global truncation error)。
利用泰勒级数展开直接推导欧拉方法,可以同时推出截断误差的大小和属性。假设被积分的微分方程具有一般形式:
y ′ = f ( x , y ) y' = f(x, y) y′=f(x,y)(2.5)
其中, y ′ = d y / d x y' = dy/dx y′=dy/dx,x和y分别为自变量和因变量。
如果解(也就是描述y行为的函数)具有连续导数,那么它可以在点(xi, yi)处展开成泰勒级数,即
y i + 1 = y i + y i ′ ∗ h + y i ′ ′ 2 ! ∗ h 2 + . . . + y i ( n ) n ! ∗ h n + R n y_{i+1}=y_i+y'_i*h+\frac{y''_i}{2!}*h^2+...+\frac{y^{(n)}_i}{n!}*h^n + R_n yi+1=yi+yi′∗h+2!yi′′∗h2+...+n!yi(n)∗hn+Rn(2.6)
其中, h = ( x i + 1 − x i ) h = (x_{i+1}-x_i) h=(xi+1−xi), R n R_n Rn为余项,定义为:
R n = y ( n + 1 ) ( ξ ) ( n + 1 ) ! ∗ ( h ) ( n + 1 ) R_n = \frac{y^{(n+1)}(\xi)}{(n+1)!}*(h)^{(n+1)} Rn=(n+1)!y(n+1)(ξ)∗(h)(n+1)(2.7)
其中, ξ ∈ [ x i , x i + 1 ] \xi \in [x_{i}, x_{i+1}] ξ∈[xi,xi+1]。
由于 y ′ = f ( x , y ) y' = f(x, y) y′=f(x,y),所以 y ′ ′ = f ′ ( x , y ) y'' = f'(x, y) y′′=f′(x,y), y ′ ′ ′ = f ′ ′ ( x , y ) y''' = f''(x, y) y′′′=f′′(x,y),依此类推,代入式(2.6)右边,同时也加入式(2.7),得到:
y i + 1 = y i + f ( x i , y i ) ∗ h + f ′ ( x i , y i ) 2 ! ∗ h 2 + . . . + f ( n − 1 ) ( x i , y i ) n ! ∗ h n + O ( h n + 1 ) y_{i+1}=y_i+ f(x_i, y_i)*h+\frac{ f'(x_i, y_i)}{2!}*h^2+...+\frac{f^{(n-1)}(x_i, y_i)}{n!}*h^n + O(h^{n+1}) yi+1=yi+f(xi,yi)∗h+2!f′(xi,yi)∗h2+...+n!f(n−1)(xi,yi)∗hn+O(hn+1)(2.8)
此处 O ( h n + 1 ) O(h^{n+1}) O(hn+1)表示局部截断误差与步长的n+1次幂成正比。
因为我们仅使用了泰勒级数的有限项来逼近真解,所以就产生了截断误差。这样,我们就截断或者略去了一部分真实解。例如,在前面的计算中,我们采用 y i + 1 = y i + f ( x i , y i ) × h y_{i+1} = y_{i} + f(x_i, y_i) \times h yi+1=yi+f(xi,yi)×h来计算下一个点的值,有部分泰勒级数展开项没有被包括在式中,这些剩余项就导致了欧拉方法的截断误差:
E t = f ′ ( x i , y i ) 2 ! ∗ h 2 + . . . + f ( n − 1 ) ( x i , y i ) n ! ∗ ( h ) n + O ( h n + 1 ) E_t = \frac{ f'(x_i, y_i)}{2!}*h^2+...+\frac{f^{(n-1)}(x_i, y_i)}{n!}*(h)^n + O(h^{n+1}) Et=2!f′(xi,yi)∗h2+...+n!f(n−1)(xi,yi)∗(h)n+O(hn+1)(2.9)
E t E_t Et为真实的局部截断误差。
当h足够小时,式(2.9)中各项的误差通常随着阶数的增加而减少。于是常常可以表示为:
E a = f ′ ( x i , y i ) 2 ! ∗ h 2 E_a = \frac{ f'(x_i, y_i)}{2!}*h^2 Ea=2!f′(xi,yi)∗h2(2.10)
或者:
E a = O ( h 2 ) E_a =O(h^2) Ea=O(h2)(2.11)
E t E_t Et为近似的局部截断误差。
泰勒级数给出了一种量化欧拉方程误差的方法。不过,这种方法使用时存在局限:
(1)泰勒级数仅能估计局部截断误差一即方法在一步迭代中所产生的误差。它不能估量传播截断误差,因此也不能估量全局截断误差。
(2)实际问题中处理的函数一般比简单多项式复杂。因此,计算泰勃级数展开时,导数值有时很难得到。
尽管这些限制使泰勒级数无法分析人多数实际问题的精确误差,但是它仍然有助于了解欧拉方法的性态。按照式(2.11)可发现局部误差与步长的平方和微分方程的一阶导数成正比。此外已经证明,全局截断误差为O(h),全局截断误差与步长成正比(Carnahan等人,1969)。
结论:
(1)缩短步长可以减少误差。
(2)因为直线的二阶导数为常数,所以如果基本函数(即微分方程的解)是线性的,那么方法能给出无误差的预测值。
由于欧拉方法使用直线段来逼近解,因此,欧拉方法称为一阶方法(first-order method)。
思考:如果使用二次来逼近解,也就是二阶方法,就能给出基本函数(即微分方程的解)是二次的问题的精确。同理,如果基本函数是n次多项式,则使用n阶方法可得出精确解。
2.1.3 欧拉方法的改进思路1——添加高阶项
减小欧拉方法的误差的一种方法是,在公式中加入泰勒级数展开的高阶项。例如,添加二阶项后,得到:
y i + 1 = y i + f ( x i , y i ) ∗ h + f ′ ( x i , y i ) 2 ! ∗ h 2 y_{i+1}=y_i+ f(x_i, y_i)*h+\frac{ f'(x_i, y_i)}{2!}*h^2 yi+1=yi+f(xi,yi)∗h+2!f′(xi,yi)∗h2(2.12)
于是局部截断误差变为:
E a = f ′ ′ ( x i , y i ) 3 ! ∗ h 3 E_a = \frac{ f''(x_i, y_i)}{3!}*h^3 Ea=3!f′′(xi,yi)∗h3(2.13)
尽管添加高阶项对于处理多项式来说十分简单,不过有时候会使常微分方程变得更加复杂。特别地,如果常微分方程同时为自变量和因变量的函数,就需要通过链式法则来计算微分。例如,f(x,y)的一阶导数是:
f ′ ( x , y ) = ∂ f ( x i , y i ) ∂ x + ∂ f ( x i , y i ) ∂ y d y d x f'(x,y) = \frac{ \partial{f(x_i, y_i)}}{\partial{x}} + \frac{ \partial{f(x_i, y_i)}}{\partial{y}}\frac{dy}{dx} f′(x,y)=∂x∂f(xi,yi)+∂y∂f(xi,yi)dxdy
二阶导数是:
f ′ ′ ( x , y ) = ∂ [ ∂ f / ∂ x + ( ∂ f / ∂ y ) ( d y / d x ) ] ∂ x + ∂ [ ∂ f / ∂ x + ( ∂ f / ∂ y ) ( d y / d x ) ] ∂ y d y d x f''(x,y) = \frac{ \partial[\partial{f}/\partial{x} + (\partial{f}/\partial{y})(dy/dx) ]}{\partial{x}} + \frac{ \partial[\partial{f}/\partial{x} + (\partial{f}/\partial{y})(dy/dx) ]}{\partial{y}}\frac{dy}{dx} f′′(x,y)=∂x∂[∂f/∂x+(∂f/∂y)(dy/dx)]+∂y∂[∂f/∂x+(∂f/∂y)(dy/dx)]dxdy
高阶导数会变得越来越复杂。而综合其计算量,其在性能上其实与一阶泰勒级数方法差不多,而一阶泰勒展开的欧拉方法只需要计算一阶导数,实现起来会简洁很多。因此,添加高阶项的方法其实并不是很实用。
2.1.4 欧拉方法的改进思路2——对斜率采用更好的估值方法
在“注意1”中我们提到,欧拉方法是将区间左端点处的斜率当作斜率在整个区间上平均值的逼近。但估值毕竟是估值,不是精确值,所以这个估值的精确度会严重影响计算的结果。
于是我们思考,有没有什么其他估计斜率的其他方法,能够给出更好的估值,从而得到更精确的预测值。
基于这个想法,下面给出了两种简单的修正方法来克服这个估值不精确的问题:修恩法和中点方法。
(这两种方法其实都属于一个更广泛的类型—龙格一库塔法。)
2.1.4.1 修恩法
改进斜率估计值的一种方法是,在区间上计算两个导数值:一个在区间的起始点处,一个在区间的终点处。然后,将这两个导数的平均值作为斜率在整个区间上的改进估计值。这种方法,称为修恩法(Heun’s method),其示意图如下图所示。
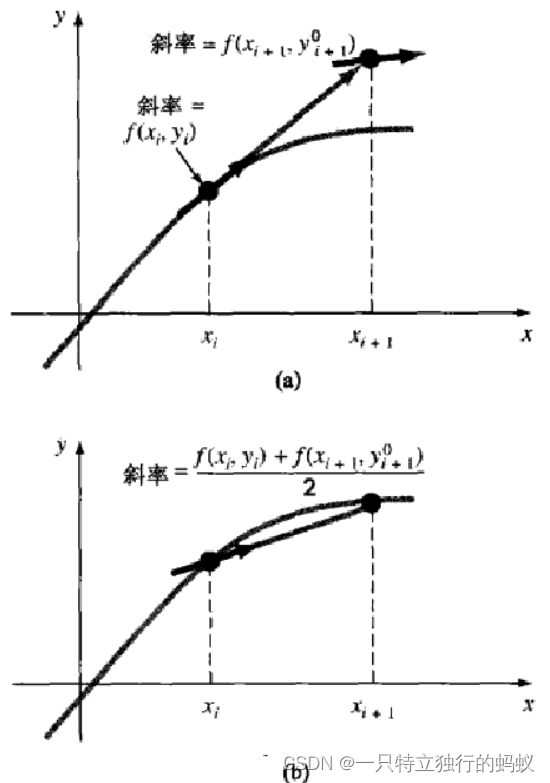
图5 修恩法的示意图:(a)预估和(b)校正
前面介绍过,在欧拉方法中,区间起始点处的斜率为:
y i ′ = f ( x i , y i ) y_i' = f(x_i, y_i) yi′=f(xi,yi) (2.15)
利用这个值线性外推出 y i + 1 y_{i+1} yi+1:
y i + 1 0 = y i + f ( x i , y i ) h y^0_{i+1} = y_i + f(x_i, y_i)h yi+10=yi+f(xi,yi)h (2.16)
标准的欧拉方法算到这一步就停止了。然而,在修恩法中,由式(2.16)得出的 y i + 1 0 y^0_{i+1} yi+10并不是最终结果,而是一个中间的预测值。式(2.16)称为预估表达式(predictor equation)。该式给出了 y i + 1 y_{i+1} yi+1的一个估计值,利用这个估计值又可以计算区间终点处的斜率(形式如式(2.15)):
y i + 1 ′ = f ( x i + 1 , y i + 1 0 ) y_{i+1}' = f(x_{i+1}, y^0_{i+1}) yi+1′=f(xi+1,yi+10) (2.17)
我们得到两个斜率估计值 y i ′ y_{i}' yi′和 y i + 1 ′ y_{i+1}' yi+1′(式(2.15)和式(2.17)),于是可以计算斜率的区间平均值:
y i ˉ ′ = y i ′ + y i + 1 ′ 2 = f ( x i , y i ) + f ( x i + 1 , y i + 1 0 ) 2 \bar{y_i}' = \frac{y_i' + y_{i+1}'}{2} = \frac{ f(x_i, y_i) + f(x_{i+1}, y^0_{i+1})}{2} yiˉ′=2yi′+yi+1′=2f(xi,yi)+f(xi+1,yi+10) (2.18)
然后,按照欧拉方法,利用这个平均斜率由 y i y_i yi线性外推出 y i + 1 y_{i+1} yi+1:
y i + 1 = y i + f ( x i , y i ) + f ( x i + 1 , y i + 1 0 ) 2 h y_{i+1} = y_i + \frac{ f(x_i, y_i) + f(x_{i+1}, y^0_{i+1})}{2} h yi+1=yi+2f(xi,yi)+f(xi+1,yi+10)h (2.19)
此式称为校正表达式((corrector equation)。
修恩法是一种预估一校正方法{predictor-corrector approach)。
修恩法可简洁地表示为:
预估: y i + 1 0 = y i + f ( x i , y i ) h y^0_{i+1} = y_i + f(x_i, y_i)h yi+10=yi+f(xi,yi)h (2.16)
校正: y i + 1 = y i + f ( x i , y i ) + f ( x i + 1 , y i + 1 0 ) 2 h y_{i+1} = y_i + \frac{ f(x_i, y_i) + f(x_{i+1}, y^0_{i+1})}{2} h yi+1=yi+2f(xi,yi)+f(xi+1,yi+10)h (2.19)
迭代修恩法:
因为式(2.19)的等号两边都含有 y i + 1 y_{i+1} yi+1,所以该式可以按迭代方式计算,可以反复使用旧的估计值计算出改进后的 y i + 1 y_{i+1} yi+1值。// 需要注意的是,这个迭代过程并不一定能收敛到真实解,不过它将收敛到一个截断误差有限的估计值。
校正过程收敛的终止条件为:
∣ ε a ∣ = ∣ y i + 1 j − y i + 1 j − 1 y i + 1 j ∣ 100 % |\varepsilon_a| = |\frac{y^j_{i+1} - y^{j-1}_{i+1}}{y^j_{i+1}}|100\% ∣εa∣=∣yi+1jyi+1j−yi+1j−1∣100%
其中, y i + 1 j − 1 y^{j-1}_{i+1} yi+1j−1和 y i + 1 j y^j_{i+1} yi+1j分别为上一校正步的结果和当前校正步的结果。
// 前面没有迭代校正的修恩法,可称为简单修恩法;经过迭代计算校正的修恩法,可以称为迭代修恩法。
特殊情况:
在前面的例子中,导数 d y / d x dy/dx dy/dx同时为因变量y和自变量x的函数( d y / d x = f ( x , y ) dy/dx = f(x,y) dy/dx=f(x,y))。对于常微分方程仅与自变量有关的情况( d y / d x = f ( x ) dy/dx = f(x) dy/dx=f(x)),求解过程中并不需要预估步(式(2.16)),而且每次迭代中也只需一次校正。在这种情况下,方法简化为
y i + 1 = y i + f ( x i ) + f ( x i + 1 ) 2 h y_{i+1} = y_i + \frac{ f(x_i) + f(x_{i+1})}{2} h yi+1=yi+2f(xi)+f(xi+1)h (2.19)
该式与“数值积分方法的总结”第1.1.1节 梯形法则(2点积分)其实是等价的。相应的截断误差也与梯形法则一样为:
E t = − f ′ ′ ( ξ ) 12 h 3 E_t = - \frac{f''(\xi)}{12}h^3 Et=−12f′′(ξ)h3
由于真解是二次多项式时,常微分方程的二阶导数为0,所以方法是二阶精度的。另外,局部和全局误差分别为 O ( h 3 ) O(h^3) O(h3)和 O ( h 2 ) O(h^2) O(h2),因此,减小步长时,误差减小的速度比欧拉方法快。
2.1.4.2 中点方法
图5和式(2.16)( y i + 1 0 = y i + f ( x i , y i ) h y^0_{i+1} = y_i + f(x_i, y_i)h yi+10=yi+f(xi,yi)h )使用了端点处的值 y i + 1 y_{i+1} yi+1 来修正斜率的。
那么是不是也可以考虑用中点处的值来修正斜率??
于是产生了另一种简单的欧拉方法的修正方法(如图6所示)。该方法称为中点方法(midpoint method)(或改进的多边形法(improved polygon),或修正的欧拉方法(modified Euler)),利用欧拉方法预测区间中点处的y值(图6(a)):
y i + 1 / 2 = y i + f ( x i , y i ) h / 2 y_{i+1/2} = y_i + f(x_i, y_i)h/2 yi+1/2=yi+f(xi,yi)h/2 (2.20)
然后用这个值来计算中点处的斜率:
y i + 1 / 2 ′ = f ( x i + 1 / 2 , y i + 1 / 2 ) y_{i+1/2}' = f(x_{i+1/2}, y_{i+1/2}) yi+1/2′=f(xi+1/2,yi+1/2) (2.21)
假设这个值是对整个区间的斜率平均值的有效近似,那么由 x i x_i xi线性外推出 x i + 1 x_{i+1} xi+1处的值为:
y i + 1 = y i + f ( x i + 1 / 2 , y i + 1 / 2 ) h y_{i+1} = y_i + f(x_{i+1/2}, y_{i+1/2}) h yi+1=yi+f(xi+1/2,yi+1/2)h (2.22)
// 注意对比式(2.20)、(2.20)、(2.20)与 (2.16)、 (2.17)、 (2.19),就可以清晰地看出中点法和修恩法的区别。
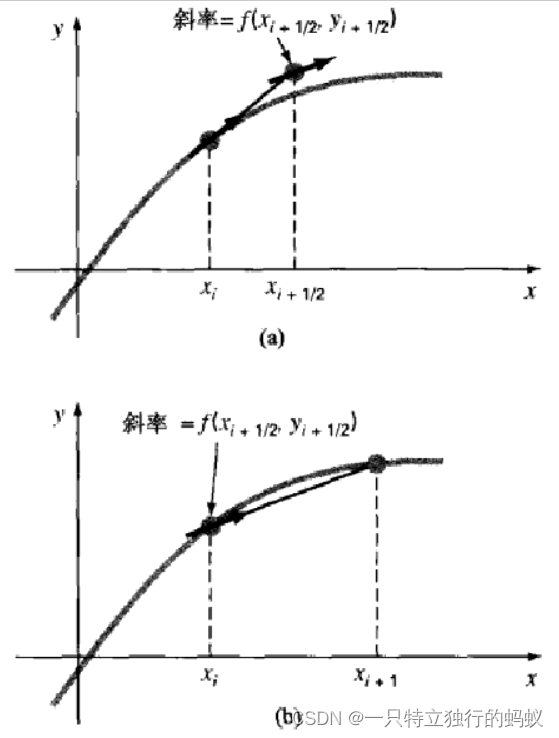
图6 中点公式的示意图。(a)式(2.20)}和(b)式(2.22)
因为式(2.22)只有等式的一边含 y i + 1 y_{i+1} yi+1,所以这种方法的结果无法像修恩法一样采用迭代校正的办法来改进。
(本方法也可同牛顿一柯特斯开型公式的中点公式结合起来理解。)
因为中点方法利用区间中点处的斜率估计值,它理论上比端点(起点)处的斜率估计值要更好(//关于数值微分的讨论知,中心有限差分逼近导数的效果比前向或后向差分都要好),所以中点方法优于欧拉方法。中点方法的局部和全局误差分别为 O ( h 3 ) O(h^3) O(h3)和 O ( h 2 ) O(h^2) O(h2)。
2.1.5 欧拉方法的改进思路3
思考:上一节提到的中点法,就类似计算积分的时候,取中点计算估值(1点积分);修恩法,就类似于梯形法计算积分(2点积分)。回想在“数值积分方法的总结”积分计算中,除了梯形法则(2点积分),我们还讲到了3点积分和4点积分,区别就在于用二次曲线和三次曲线来逼近使积分结果更加接近真实值。那么,这个地方,如果我们能计算或者估算出三个点或者四个点,是否也能用类似的方法,使求解的结果更接近真实值?
2.2 龙格-库塔法
龙格一库塔法(Range-Kutta)(RK)无需计算高阶导数,也可以达到与泰勒级数方法同样的精度。龙格一库塔法存在许多不同版本,但它们都可以写成式(25.1)的一般形式
y i + 1 = y i + ϕ ( x i , y i , h ) h y_{i+1} = y_i + \phi(x_i, y_i, h)h yi+1=yi+ϕ(xi,yi,h)h (2.23)
其中, ϕ ( x i , y i , h ) \phi(x_i, y_i, h) ϕ(xi,yi,h)称为增量函数((increment function),它表示整个区间上的斜率。增量函数的一般形式是

k1出现在k2的表达式中,k2又出现在k3的表达式中,等等。因为每个k都是由函数赋值的,所以这种
递归关系提高了龙格-库塔法的计算效率。
将增量函数的项数记为n,n值的不同就对应着不同类型的龙格一库塔法。n=1时,一阶龙格-库塔法,实际上就是欧拉方法。
(未完待续,更新中。。。)
相关文章:

常微分方程(ODE)求解方法总结
常微分(ODE)方程求解方法总结 1 常微分方程(ODE)介绍1.1 微分方程介绍和分类1.2 常微分方程的非计算机求解方法1.3 线性微分方程求解的推导过程 2 一阶常微分方程(ODE)求解方法2.1 欧拉方法2.1.1 欧拉方法2…...

【华为OD机试】区间交集【2023 B卷|200分】
【华为OD机试】-真题 !!点这里!! 【华为OD机试】真题考点分类 !!点这里 !! 题目描述 给定一组闭区间,其中部分区间存在交集。 任意两个给定区间的交集,称为公共区间 (如:[1,2],[2,3]的公共区间为[2,2],[3,5],[3,6]的公共区间为[3,5])。 公共区间之间若存在交集,则需…...

Vue3 | Element Plus resetFields不生效
Vue3 | Element Plus resetFields不生效 1. 简介 先打开创建对话框没有问题,但只要先打开编辑对话框,后续在打开对话框就会有默认值,还无法使用resetFields()重置。 下面是用来复现问题的示例代码和示例GIF。 <script setup> import…...

机器视觉特点 机器视觉实际应用
机器视觉特点 1、机器视觉是一项综合技术,其中包括数字图像处理技术,机械工程技术,控制技术,电光源照明技术,光学成像技术,传感器技术,模拟与数字视频技术,计算机硬件技术ÿ…...
elementui大型表单校验
一般很大的表单都会被拆解开,校验,,不会写在一个页面,,就会有多个 el-form ,,主页要集合所有el-form的数据,,所以有一个map来接收,传送表单数据,&…...

Linux+Selenium
SeleniumLinux 开源社区已无CentOS7.0以下rpm维护。升级测试机器到CentOS7.X。 Selenium安装 python环境:pip3 install selenium 浏览器插件:http://chromedriver.storage.googleapis.com/index.html yum instlal google-chrome 使用以下命令确定是…...
)
2023-06-01 LeetCode每日一题(礼盒的最大甜蜜度)
2023-03-29每日一题 一、题目编号 二、题目链接 点击跳转到题目位置 三、题目描述 给你一个正整数数组 price ,其中 price[i] 表示第 i 类糖果的价格,另给你一个正整数 k 。 商店组合 k 类 不同 糖果打包成礼盒出售。礼盒的 甜蜜度 是礼盒中任意两…...

Spring架构篇--2.7.2 远程通信基础--Netty原理--ServerBootstrap
前言:已经初始化了NioEventLoopGroup 的boosGroup 和 workerGroup ,那么ServerBootstrap的作用是干嘛的呢 ,本文在Spring架构篇–2.7.1 远程通信基础–Netty原理–NioEventLoopGroup 之后继续进行探究 1 首先回顾下 nettt 的使用demo&#x…...

awk编辑器
文章目录 一.awk概述1.概述2.作用3.awk的工作过程4.awk 工作原理及命令格式5.awk的基本操作及其内置变量5.1 awk的-F操作5.2 awk的-v操作5.3 内置变量 二.awk 打印1.基本打印用法1.1 默认打印1.2打印文件内容 2.对行进行操作2.1 只打印行号(有多少行)2.2…...
DicomObjects.Core 3.0.17 Crack
DicomObjects.NET 核心版简介 DicomObjects.Core Assembly DicomObjects.NET 核心版简介 DicomObjects.Core 由一组相互关联但独立的 .核心兼容的“对象”,使开发人员能够快速轻松地将DICOM功能添加到其产品中,而无需了解或编程DICOM标准的复杂性。此帮助…...
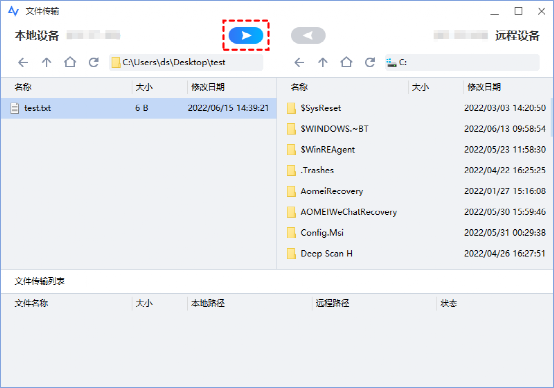
电脑怎么通过网络传输文件?
可以通过网络在电脑之间传输文件吗? “由于天气的原因,我的老板决定让所有员工在家工作。但是我很多工作文件都在公司的电脑中,怎么才能将公司的文件远程传输到我家里的电脑上?电脑可以通过网络远程传输文件吗?” …...

人工智能之深度学习
第一章 人工智能概述 1.1人工智能的概念和历史 1.2人工智能的发展趋势和挑战 1.3人工智能的伦理和社会问题 第二章 数学基础 1.1线性代数 1.2概率与统计 1.3微积分 第三章 监督学习 1.1无监督学习 1.2半监督学习 1.3增强学习 第四章 深度学习 1.1神经网络的基本原理 1.2深度…...

性能测试设计阶段
性能测试设计阶段 性能测试是软件测试中的关键环节,它可以帮助我们评估软件系统在压力下的运行稳定性和性能表现。性能测试设计阶段是性能测试的基础,只有经过充分的设计,才能保证性能测试的有效性和准确性。 在性能测试设计阶段,…...

leetCode !! word break
方法一:字典树动态规划 首先,创建node类,每个对象应该包含:一个node array nexts(如果有通往’a’的路,那么对应的nexts[0]就不该为null); 一个boolean 变量(如果到达的这个字母恰好是字典中某个候选串的结尾,那么 标记…...

基础学习——关于list、numpy、torch在float和int等数据类型转换方面的总结
系列文章目录 Numpy学习——创建数组及常规操作(数组创建、切片、维度变换、索引、筛选、判断、广播) Tensor学习——创建张量及常规操作(创建、切片、索引、转换、维度变换、拼接) 基础学习——numpy与tensor张量的转换 基础学习…...

华纳云美国Linux服务器常用命令分享
美国Linux服务器系统目前也是跟Windows操作系统一样用户量非常多,其简单的纯命令操作模式可以节省很多系统空间,本文小编就来分享一些美国Linux服务器系统常用的命令,希望能够给刚入门的美国Linux服务器系统的用户提供一些操作参考。 1、系统…...

【minio】8.x版本与SpringBoot版本不兼容报错
错误异常: <minio.version>8.4.3</minio.version><spring-boot.version>2.6.13</spring-boot.version>Description:An attempt was made to call a method that does not exist. The attempt was made from the following location:io.min…...
如何用chatGPT赚钱?
赚钱思路 1)初级-账号 对于新事物的出现,很多人对此都是抱着一个看热闹的态度,大家对于这个东西的整体认知水平是很低的! 所以这个时候的思路就是快速去抢占市场,去各个平台发一些和ChatGPT相关的视频和文章去抢占市…...
【Go编程语言】流程控制
流程控制 文章目录 流程控制一、if 语句1.if 嵌套语句 二、switch 语句三、for 循环四、string 程序的流程控制结构一具有三种:顺序结构,选择结构,循环结构 顺序结构:从上到下,逐行执行。默认的逻辑 选择结构…...
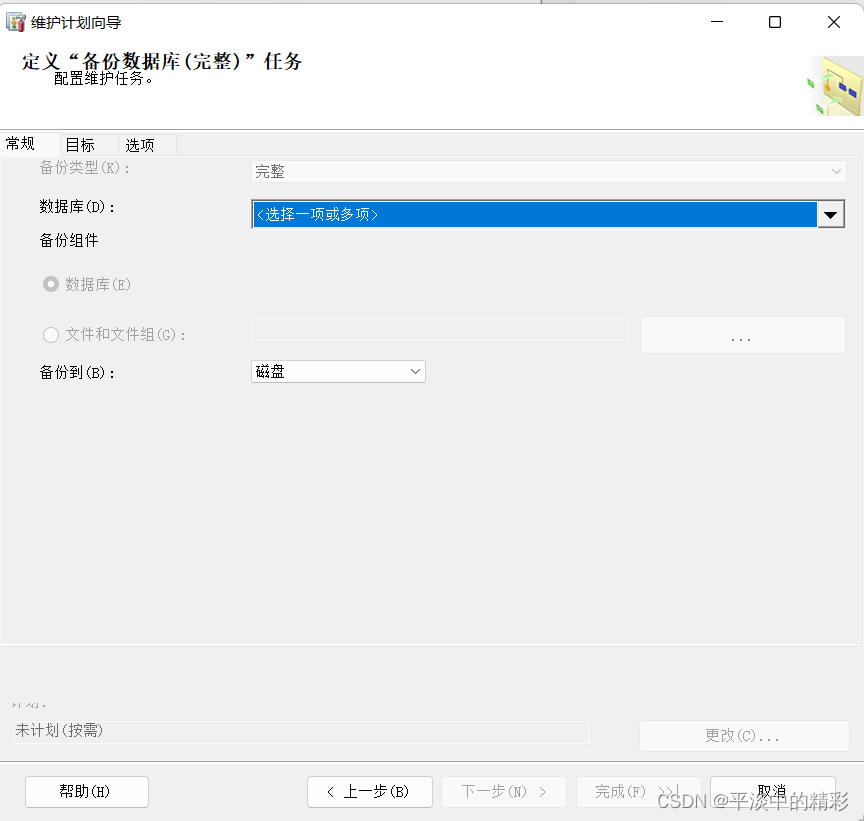
Sql Server 自动备份
Sql Server 自动备份 文章目录 Sql Server 自动备份1. 打开SQL Server,在管理下找到”维护计划”,右键点击”维护计划向导”,如图;2. 再次点击维护计划向导3. 在选择维护任务下勾选”备份数据库”、”清楚维护任务”4.选择需要备份…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...
