交直流系统潮流计算及相互关联特性分析(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
2.1 整流侧定电流,逆变侧定电压
2.2 整流侧定电流,逆变侧定熄弧角
2.3 整流侧定功率,逆变侧定电压
2.4 整流侧定功率,逆变侧定熄弧角
2.5 整流侧定触发角,逆变侧定电流
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
文献来源:

随着交直流输电系统的网络结构日益复杂,传统的纯交流潮流算法受到挑战,国内外学者对此进行了研究。截至到目前,交直流系统的潮流算法分为两大类:统一计算和交替迭代计算4。直流输电系统平衡方程包括换流器的稳态方程以及相关控制方程,统一潮流算法将交流与直流平衡方程同时求解。与其不同,交替迭代算法将两者分离计算,第一步将直流线路作为等值PQ负荷,求解交流系统状态量;第二步求解直流系统状态量,将第一步求解得到的交流端电压设为恒定值[5]。
在交直流转换过程中,换流装置吸收的无功功率约为所传输的直流功率的-一半,其中逆变器吸收的无功功率更多,能达到60%左右[14-15]。在传统电压稳定性分析方法的基础上得知,若受端交流系统无功供给不足,交直流系统会发生严重的电压失稳现象,尤其是逆变站受端电网交直流混合节点。
目前来说,人们主要从静态、动态两个角度研究交直流系统电压稳定性问题。在静态电压稳定角度,分析方法包括最大功率曲线法、短路比法、电压稳定因子分析法、特征值分析、崩溃点法等。在动态电压稳定角度,分析方法包括动态最大功率曲线法、分叉理论法、时域仿真、暂态能量函数等6]。
对于潮流算法,合适的存储结构可实现元素的快速检索、更新、存储,提高计算速度。本章算法采用支路潮流微增量为基元,使支路与雅可比矩阵直接关联;采用三角检索存储格式,存储框架不改变,只在预留的位置添加注入元,避免了繁琐的信息检索[49]。
相对于消除全部直流变量方法来说,保留直流电流变量的交直流潮流计算方法增加了雅可比矩阵的维数,与纯交流的雅可比矩阵格式有差异,但关于状态量直流电流的导数项多数为0,矩阵的稀疏度依然较高。以交流潮流部分的存储技术为基础,为保持其雅可比格式最大化相容,该算法按照不同的控制方式,将直流输电线路等效成相应的节点与线路,在相应的存储数组上作相应的变化。
以文献[49]阐述的封闭存储框架为基础,阐述添加直流输电单元对存储检索技术的影响。以一条直流输电线路为例,整流器节点为i,逆变器节点k,分析在不同控制方式下存储格式的调整。假设n为电网总节点数,b为考虑虚拟支路的总支路数,直流输电单元个数分别为a,临时指针 pt,同时定义的各存储数组,变化如下:

📚2 运行结果
2.1 整流侧定电流,逆变侧定电压

2.2 整流侧定电流,逆变侧定熄弧角

2.3 整流侧定功率,逆变侧定电压

2.4 整流侧定功率,逆变侧定熄弧角

2.5 整流侧定触发角,逆变侧定电流
部分代码:
%% 直流节点编号
D_CN=Hvdc.con(:,[1 2])';%直流节点编号
A_CN=setdiff(1:n,union(D_CN,SW.con(1,1)))';
N_DC=size(D_CN,1);%直流节点个数
N_AC=size(A_CN,1);%交流节点个数
P_N=setdiff(1:n,SW.con(1,1))';
Q_N=setdiff(P_N,PV.con(:,1));
P_N=intersect(A_CN, P_N);%交流节点P方程节点
Q_N=intersect(A_CN, Q_N);%交流节点Q方程节点
P=size(P_N,1); %交流节点P方程个数
Q=size(Q_N,1); %交流节点Q方程个数
% YK=zeros(P+Q);
DPa=zeros(P,1);
DQa=zeros(Q,1);
DPt=zeros(N_DC,1);
DQt=zeros(N_DC,1);
Dd1=zeros(N_DC,1);
Dd2=zeros(N_DC,1);
Dd3=zeros(N_DC,1);
Dd4=zeros(N_DC,1);
Dd5=zeros(1,1);
H=zeros(P+N_DC);
N=zeros(P+N_DC,Q+N_DC);
M=zeros(Q+N_DC,P+N_DC);
L=zeros(Q+N_DC);
JRX=zeros(9,9);
%% 直流迭代初值设置+控制方式
V_d=ones(N_DC,1)*1.1562;%直流电压初值
I_D=0.5;
% fai=ones(N_DC,1)*30/180*pi;%功率因数角初值30°
P_d=0.6.*ones(N_DC,1);
Qd=0.3.*ones(N_DC,1);
Sd=0.5.*ones(N_DC,1);
Control_ang=[20/180*pi;17/180*pi];%换流器控制角,第一个为alpha,第二个为gama
% Control_ang(2)=30/180*pi;
W=cos(Control_ang);
K_T=ones(N_DC,1);%直流支路两端变压器变比值设置
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]王云鹏. 交直流系统潮流计算及相互关联特性分析[D].山东大学,2016.
🌈4 Matlab代码实现
相关文章:

交直流系统潮流计算及相互关联特性分析(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

如何快速掌握Facebook运营+独立站运营基础?
在当今数字化时代,Facebook运营和独立站运营成为许多企业和个人创业者的关键战略。通过巧妙地结合这两个渠道,你可以有效地推广品牌、吸引目标受众并实现商业目标。本文将为你介绍如何快速掌握Facebook运营和独立站运营的基础知识,为你的业务…...
)
Java之旅(十三)
Java 类 Java类是Java编程语言中的基本构建块,是一种用户定义的数据类型,它可以被看作是一个模板或蓝图。它是对象的模板,,描述了一组具有相同特征(属性)和行为(方法)的对象。Java …...

Calibre 6.18.1 正式发布,功能强大的开源电子书工具
导读Calibre 开源项目是 Calibre 官方出的电子书管理工具。它可以查看,转换,编辑和分类所有主流格式的电子书。Calibre 是个跨平台软件,可以在 Linux、Windows 和 macOS 上运行。 Calibre 6.18.1 正式发布,此次更新内容如下&#…...

如何在C语言中定义和使用函数?
如何在C语言中定义和使用函数? 引言: 函数是C语言中的一个重要概念,它使程序能够模块化、重用和组织代码。通过将一段逻辑相关的代码封装到函数中,我们可以提高代码的可读性、可维护性和重用性。本文将详细介绍在C语言中定义和使…...

【C++】4.多媒体库:SFML库入门
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍SFML库使用。 学其所用,用其所学。——梁启超 欢迎来到我的博客,一起学习知识,共同进步。 喜欢的朋友可以关注一下,下次更新不迷路&#…...

【算法题】1717. 删除子字符串的最大得分
插: 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 坚持不懈,越努力越幸运,大家一起学习鸭~~~ 给你一个字符串 s 和两个整数 x 和 y 。你可以执行下面…...
 ABCD)
Codeforces Round 877 (Div. 2) ABCD
A. Blackboard List solve: 1、生成的数一定不是负数,所以有负数的情况下,负数一定是原来的数。 2、没有负数的情况下,最大的数一定是原来的数,因为操作只能使数变小。 void solve() {cin>>n;for(int i0;i<n;i)cin>&…...
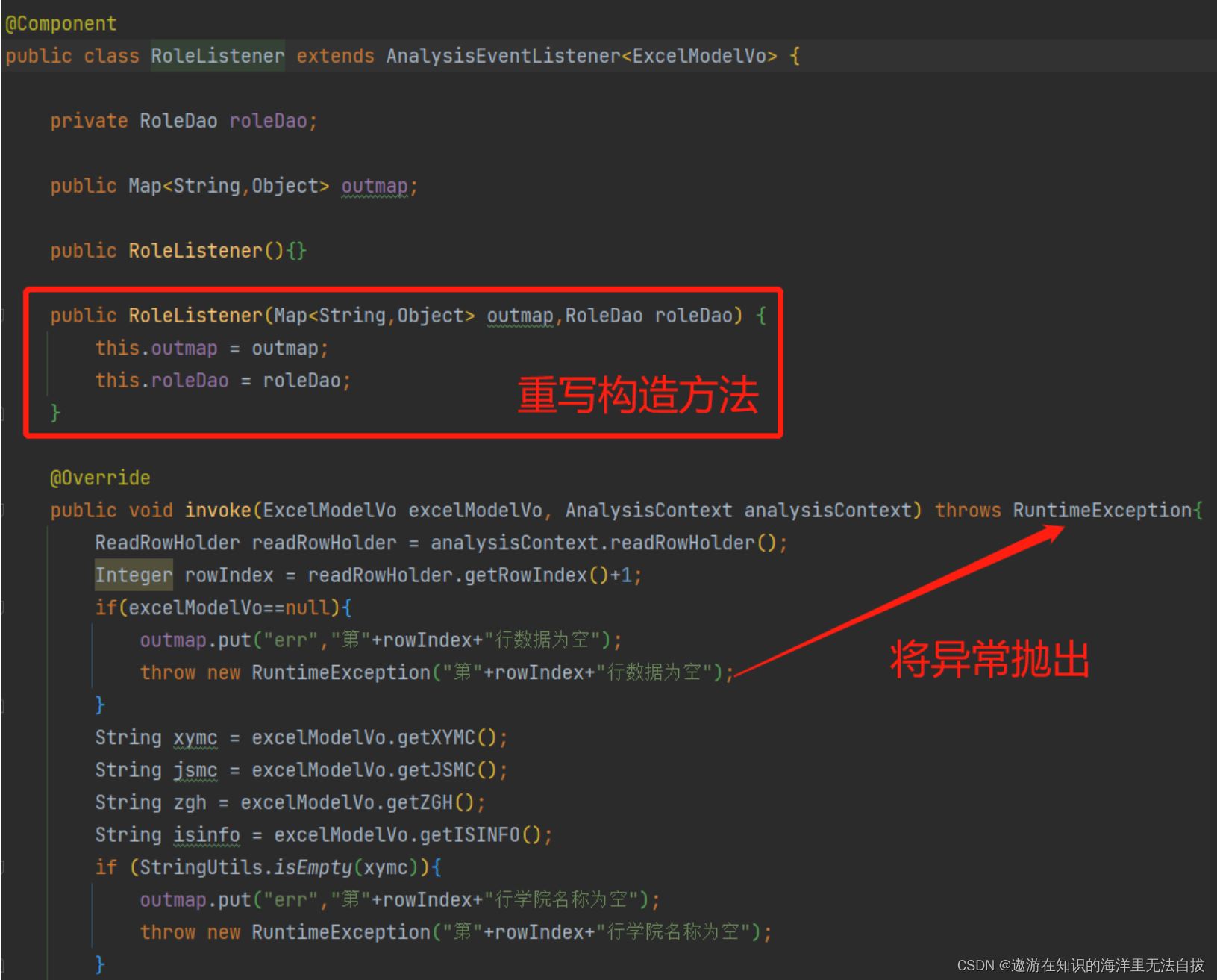
easyExcel导入失败提示用户第几行有误并回滚数据
思路: 在controller定义一个map,将map传入excel监听器,在监听器中处理excel的数据,读取到某一行出现错误就将错误提示信息存入map并抛出一个异常给service。在service方法上开启事务,并将异常出实现数据回滚࿰…...

问道价值互联网,区块链的下一个十年 | 2023 开放原子全球开源峰会区块链分论坛即将启幕
随着全球 Web3 浪潮经由数字藏品、元宇宙的日渐普及而实现落地,区块链在“信息互联网”转向“价值互联网”中的重要作用正得到进一步认可。在数字经济蓬勃发展、数据成为重要生产要素的时代,区块链已不仅仅是一项技术、一种工具,更是一种思维…...

解读 Nginx 配置
tip:作为程序员一定学习编程之道,一定要对代码的编写有追求,不能实现就完事了。我们应该让自己写的代码更加优雅,即使这会费时费力。 推荐:体系化学习Java(Java面试专题) 文章目录 1、Nginx 配…...

知识变现海哥:课程定价容易出现的三大误区
哈喽,大家好,我是海哥,知识付费变现创业教练,教育公司培训总监,从事知识付费变现咨询10年,已助力3000人实现知识付费变现。 很多做知识付费的老师都有定价方面的困惑。怕定太高,卖不出去&#…...
Android开发 LogDog (日志狗)V2.0.0
目录 一、简介 二、使用推荐 1、初始化LogDog 2、运行中如何更改初始化时的配置? 三、更改 四、新功能 1、Log过滤 2、自定义打印 3、提供占位符式打印 一、简介 LogDog V1.0 版本https://blog.csdn.net/Ym_quiet/article/details/130453232?spm1001.2014…...

JavaScript break
在JavaScript中,break语句用于提前退出或终止循环或switch语句。它允许您立即停止循环或switch的执行,并继续执行后面的代码。 以下是在循环中使用break的示例: javascript for (var i 0; i < 10; i) { if (i 5) { break; // 当…...

linux服务器使用curl命令处理常用es查询
目录 场景: 结果格式化显示: 验证服务启动: 单个参数变量查询: 分页查询: 日期范围查询: must中单个参数条件查询 must中多个参数条件查询 使用filter过滤查询 使用sort过滤查询 总结: 场景…...
Office Visio 2013安装
哈喽,大家好。今天一起学习的是Visio 2013的安装,这是一个绘制流程图的软件,用有效的绘图表达信息,比任何文字都更加形象和直观。Office Visio 是office软件系列中负责绘制流程图和示意图的软件,便于IT和商务人员就复杂…...

C++ 私有析构函数的作用
如果一个类的析构函数声明为私有(private),其他对象或函数将无法直接调用析构函数。这意味着如果你尝试使用delete操作符删除该类的对象,将会导致编译错误,因为析构函数是不可访问的。 将析构函数声明为私有是一种防止…...

【C++】deque的用法
目录 一、容器适配器二、deque的介绍三、deque的使用及缺陷1、deque的构造函数2、deque的元素访问接口3、deque的 iterator的使用4、deque的增删查改4、deque的缺陷5、为什么选择deque作为stack和queue的底层默认容器 一、容器适配器 在了解deque前,我们先讲一讲什…...

Live800:智能客服有哪些未来发展趋势?
智能客服,也称智能问答系统,是一种利用机器学习、自然语言处理等技术实现自主询问、自主应答、自主维护的自动化系统。它们可以通过文字形式,为用户提供个性化、一对一的服务,避免了人工客服的人力成本和等待时间。 未来ÿ…...

【一】Java SE 基础
文章目录 一、初始Java1.1 什么是Java1.2 Java的特点1.3 第一个Java程序 二、数据类型与变量2.1 基本数据类型2.2 基本数据类型对应的包装类2.3 变量2.4 类型转换2.5 字符串类型及其与数字之间的转换 三、运算符3.1 算术运算符3.2 赋值运算符3.3 关系运算符3.4 逻辑运算符3.5 位…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

