PAT A1087 All Roads Lead to Rome
1087 All Roads Lead to Rome
分数 30
作者 CHEN, Yue
单位 浙江大学
Indeed there are many different tourist routes from our city to Rome. You are supposed to find your clients the route with the least cost while gaining the most happiness.
Input Specification:
Each input file contains one test case. For each case, the first line contains 2 positive integers N (2≤N≤200), the number of cities, and K, the total number of routes between pairs of cities; followed by the name of the starting city. The next N−1 lines each gives the name of a city and an integer that represents the happiness one can gain from that city, except the starting city. Then K lines follow, each describes a route between two cities in the format City1 City2 Cost. Here the name of a city is a string of 3 capital English letters, and the destination is always ROM which represents Rome.
Output Specification:
For each test case, we are supposed to find the route with the least cost. If such a route is not unique, the one with the maximum happiness will be recommanded. If such a route is still not unique, then we output the one with the maximum average happiness -- it is guaranteed by the judge that such a solution exists and is unique.
Hence in the first line of output, you must print 4 numbers: the number of different routes with the least cost, the cost, the happiness, and the average happiness (take the integer part only) of the recommanded route. Then in the next line, you are supposed to print the route in the format City1->City2->...->ROM.
Sample Input:
6 7 HZH
ROM 100
PKN 40
GDN 55
PRS 95
BLN 80
ROM GDN 1
BLN ROM 1
HZH PKN 1
PRS ROM 2
BLN HZH 2
PKN GDN 1
HZH PRS 1
Sample Output:
3 3 195 97
HZH->PRS->ROM
将字符串转化为数字下标进行存储,用map来实现int和string之间的映射关系;
*
* 当题目中要 求超过三个标尺时,先用Dijkstra算法求出每个顶点的前驱节点,
* 即u是由哪个点哪个点(哪些点)转化过来能使d[u] 的值变小,使d[u]变小的
* 点就是应该求的u的前驱节点;
/*** 将字符串转化为数字下标进行存储,用map来实现int和string之间的映射关系;* * 当题目中要 求超过三个标尺时,先用Dijkstra算法求出每个顶点的前驱节点,* 即u是由哪个点哪个点(哪些点)转化过来能使d[u] 的值变小,使d[u]变小的* 点就是应该求的u的前驱节点;
*/#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <map>using namespace std;const int N = 210, INF = 1e9;
int g[N][N], d[N], w[N]; //图,距离数组,幸福值数组
bool hs[N];
int Nv, Ne, st, ed; //顶点数目,边数目,起点,终点
int idx; //字符转化为数字的下标编号//最小花费,最大幸福值,最大平均幸福值,最短路径数目
int MINC = INF, MAXH, MAXA, num;
vector<int> temp, path; //路径编号
vector<int> pre[N]; //前驱节点
map<int, string> idx_city; //字符串与数字编号的一一映射
map<string, int> city_idx;int add(string s)
{city_idx[s] = idx;idx_city[idx] = s;return idx++;
}void Read()
{fill(*g, *g+N*N, INF); //初始化string sta;cin >> Nv >> Ne >> sta;st = add(sta);for(int i=1; i<Nv; ++i){string s;int hap;cin >> s >> hap;int u = add(s);w[u] = hap;}ed = city_idx["ROM"];for(int i=0; i<Ne; ++i){string a, b;int u, v, cost;cin >> a >> b >> cost;u = city_idx[a], v = city_idx[b];g[u][v] = g[v][u] = min(g[u][v], cost);}
}void Dijkstra(int st)
{fill(d, d+N, INF);d[st] = 0;for(int i=0; i<Nv; ++i){int MIN = INF, u = -1;for(int j=0; j<Nv; ++j)if(hs[j] == 0 && d[j] < MIN){MIN = d[j];u = j;}if(u == -1) return;hs[u] = 1;for(int j=0; j<Nv; ++j)if(hs[j] == 0 && g[u][j] != INF){int cost = g[u][j];if(d[u] + cost < d[j]){d[j] = d[u] + cost;pre[j].clear();pre[j].push_back(u);}else if(d[u] + cost == d[j])pre[j].push_back(u);}}
}void dfs(int v)
{if(v == st){temp.push_back(v);++num; int cost = 0, hap = 0;for(int j=temp.size()-1; j>0; --j){int fs = temp[j], sc = temp[j-1];cost += g[fs][sc];hap += w[sc];}int avg = hap / (temp.size() - 1);//求平均值没有算起点;if(cost < MINC) {MINC = cost;MAXH = hap;MAXA = avg;path = temp;}else if(cost == MINC && hap > MAXH){MAXH = hap;MAXA = avg;path = temp;}else if(cost == MINC && hap == MAXH && avg > MAXA){MAXA = avg;path = temp;}temp.pop_back();return;}temp.push_back(v);for(auto ele : pre[v])dfs(ele);temp.pop_back(); //回溯
}void Print()
{cout << num << ' ' << MINC << ' ' << MAXH << ' ' << MAXA << endl;for(int i=path.size()-1; i>=0; --i){if(i != path.size()-1) cout << "->";cout << idx_city[path[i]];}
}int main()
{Read();Dijkstra(st);dfs(ed);Print();return 0;
}相关文章:

PAT A1087 All Roads Lead to Rome
1087 All Roads Lead to Rome 分数 30 作者 CHEN, Yue 单位 浙江大学 Indeed there are many different tourist routes from our city to Rome. You are supposed to find your clients the route with the least cost while gaining the most happiness. Input Specific…...

浅谈HttpURLConnection所有方法详解
HttpURLConnection 类是 Java 中用于实现 HTTP 协议的基础类,它提供了一系列方法来建立与 HTTP 服务器的连接、发送请求并读取响应信息。下面是 HttpURLConnection 类中常用的方法以及其详细解释: ---------------------------------------------------…...

前端快速创建web3应用模版分享
一、起因 一直以来都有一个创建前端Dapp模版的愿望,一来是工作中也有这样的需要,避免每次都要抽离重复的代码。二来是这样的模版也能帮助其他前端快速了解到web3应用的脚手架以及框架结构。于是决定整理一个模版并开源,希望我的代码能帮助到大…...

越权漏洞讲解
越权漏洞是指系统或应用程序中存在的安全漏洞,允许攻击者以超越其授权范围的方式访问系统资源或执行特权操作。这种漏洞可能会导致严重的安全风险,因为攻击者可以利用它来获取敏感信息、修改系统设置或执行恶意操作。 下面是一些常见的越权漏洞类型和它…...
短视频矩阵源码系统打包.源码
Masayl是一款基于区块链技术的去中心化应用程序开发平台,可帮助开发者快速、便捷地创建去中心化应用程序。Masayl拥有丰富的API和SDK,为开发者们提供了支持。此外,Masayl还采用了高效的智能合约技术,确保应用程序的稳定、安全和高…...

云南LED、LCD显示屏系统建设,户外、室内广告大屏建设方案
LED大屏幕显示系统是LED高清晰数字显示技术、显示单元无缝拼接技术、多屏图像处理技术、信号切换技术、网络技术等科技手段的应用综合为一体,形成一个拥有高亮度、高清晰度、技术先进、功能强大、使用方便的大屏幕投影显示系统。通过大屏幕显示系统,可以…...

Shell脚本:expect脚本免交互
Shell脚本:expect脚本免交互 expect脚本免交互 一、免交互基本概述:1.交互与免交互的区别:2.格式:3.通过read实现免交互:4.通过cat实现查看和重定向:5.变量替换: 二、expect安装:1.…...

王道考研计算机网络第二章知识点汇总
2.1.1物理层基本概念 电气特性和功能特性易混淆,注意区分。电气特性一般指的是某个范围,功能特性一般指的是电平所代表的含义。 2.1.2数据通信基础知识 同步传输是指发送方和接收方节奏是统一的,数据之间是没有间隔的是一个一个的区块。在键…...
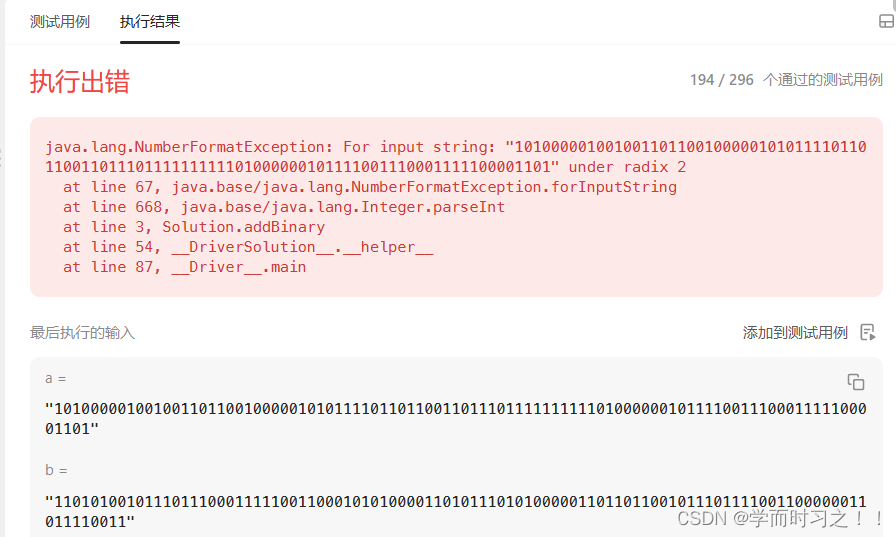
06.05
1.二进制求和 给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和。 考虑一个最朴素的方法:先将 aaa 和 bbb 转化成十进制数,求和后再转化为二进制数。利用 Python 和 Java 自带的高精度运算,我们可以很简单地写出这…...

【虹科案例】虹科数字化仪在激光雷达大气研究中的应用
01 莱布尼茨研究所使用激光雷达进行大气研究 图 1:在 Khlungsborn 的 IAP 办公室测试各种激光器 大气研究使用脉冲激光束通过测量大气中 100 公里高度的多普勒频移和反向散射光来测量沿光束的温度和风速。返回的光信号非常微弱,会被阳光阻挡,…...
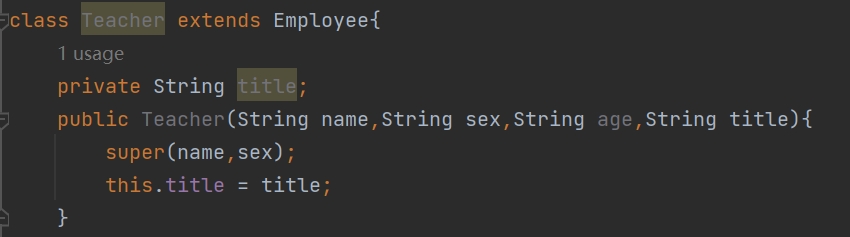
Java抽象类介绍
1 问题 声明一个名为Employee的抽象类,其中包含name(姓名)和sex(性别)两个String类型的私有属性,并声明一个继承于Employee抽象类的子类Teacher。 2 方法 2.1 定义一个抽象类:Employee。 2.2 为Employee类设计一个抽象方法。 2.3实现抽象类Em…...

适配器模式的运用
文章目录 一、适配器模式的运用1.1 介绍1.2 适配器模式结构1.3 类适配器模式1.3.1 类适配器模式类图1.3.2 代码 1.4 对象适配器模式1.4.1 对象适配器模式类图1.4.2 代码 1.5 应用场景1.6 JDK源码解析1.6.1 字节流到字符流的转换类图1.6.2 部分源码分析1.6.3 总结 一、适配器模式…...

2023/6/8总结
MySQL必知必会 commit 和 rollback 的差异是commit会提交,而rollback不会,就好像是撤回。 使用保留点: 简单的rollback和commit语句就可以写入或者撤销整个事务处理,但是,只是对简单的事务处理才能这样做࿰…...
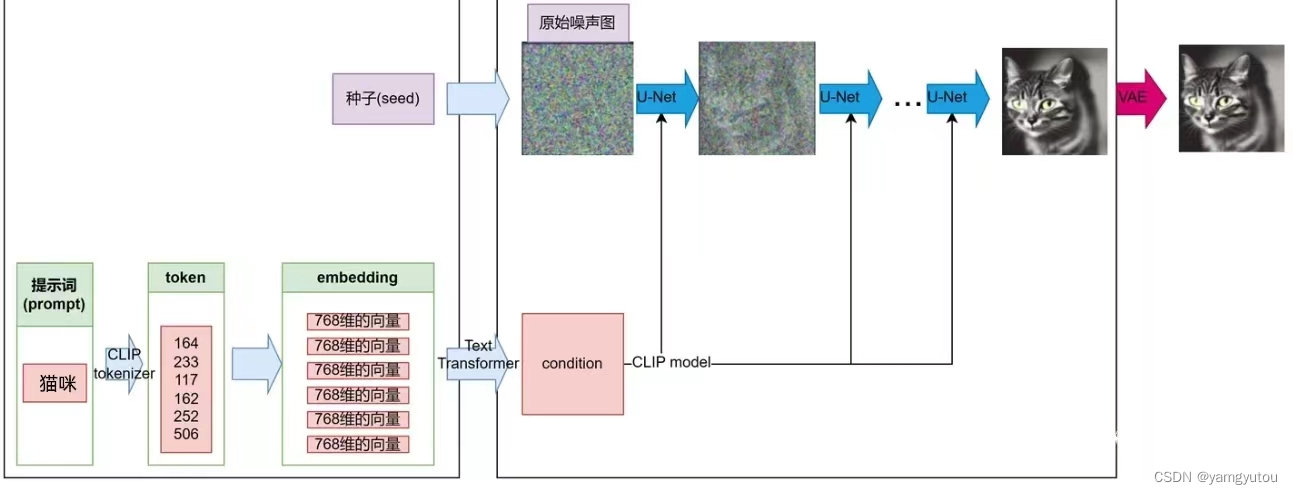
AIGC大模型之——以文生图介绍
一、什么是以文生图? 以文生图是AIGC ( AI Generated Content )框架中的一个关键技术,通过文字描述,将文字转化为图像并展示出来。以文生图具有白动化程度高、精度高、可扩展性强、可定制化等优势,具有广泛的应用前景&…...

kali学习笔记(二)
一、关闭自动锁屏 关闭自动锁屏对于测试人员来说,可以按照自己的习惯来设置,不然kali会过十分钟就锁屏,有的时候会比较不方便。 1、使用root账号登录,在display设置选项中做如下设置。 2、把休眠选项关掉。 二、创建快照 关机创…...

avx指令集判断的坑
(一)背景 项目中依赖算法同学编写的算法模块,他们在使用avx,sse指令集来提高速度,结果在一些机器上崩溃,导致项目无法发版。 我给他们说,我们项目中使用了谷歌的 libyuv 库,也使用了…...

求内推,求明主!
个人资料: 性 别: 男 年 龄: 30岁 户 籍: 湖南衡阳 专 业: 计算机科学与技术 求职意向: Java软件开发工程师/JavaWeb开发工程师 现 居 地: 深圳市龙华新区 自考本科学历,6年工作经验(做过商城,APP,小程序,也研究多个开源案例,开源项目,并提交过PR) 自我评价: 做事积极主动,有责…...

第十三章:约束
第十三章:约束 13.1:约束(constraint)概述 为什么需要约束 数据完整性(Data Integrity)是指数据的精确性(Accuracy)和可靠性(Reliability)。它是防止数据库中存在不符合语义规定的数据和防止因错误信息的输入输出造成无效操作或错误信息而提出的。 为…...

M.2 SSD接口详解
一、M.2简介 M.2接口是一种新的主机接口方案,可以兼容多种通信协议,如sata、PCIe、USB、HSIC、UART、SMBus等。 M.2接口是为超极本(Ultrabook)量身定做的新一代接口标准,以取代原来的mSATA接口。无论是更小巧的规格尺…...
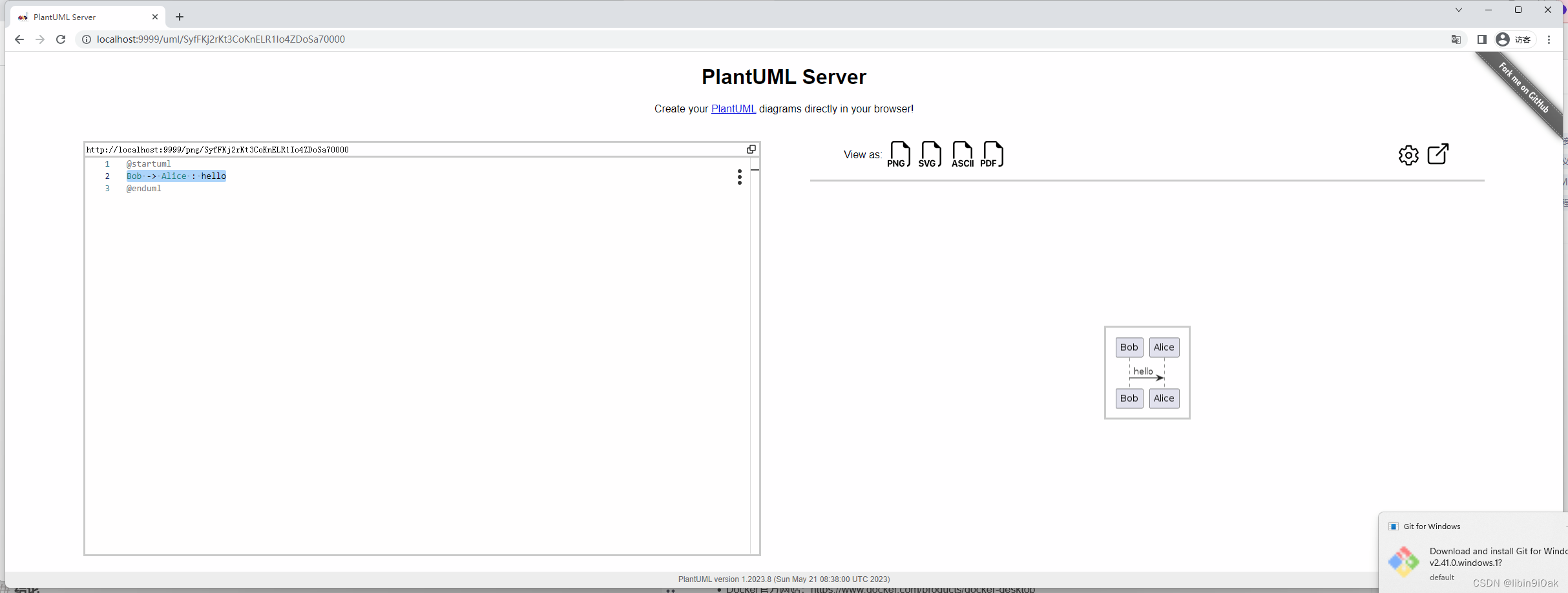
在本地Windows 11 系统的桌面版Docker上搭建PlantUML
文章目录 在本地Windows系统的桌面版Docker上搭建PlantUML简介步骤步骤 1:安装Docker Desktop步骤 2:启动Docker Desktop步骤 3:拉取PlantUML镜像步骤 4:运行PlantUML容器步骤 5:访问PlantUML Web界面 结论参考资料 结…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
