当前位置： 首页 > news >正文

苹果MacOS系统傻瓜式本地部署AI绘画Stable Diffusion教程

news 2026/2/8 18:09:04

Stable Diffusion的部署对小白来说非常麻烦，特别是又不懂技术的人。今天分享两个一键傻瓜式安装包，对小白来说非常有用。下面两个任选一个安装就可以。

一、DiffusionBee

简单介绍

DiffusionBee是基于stable diffusion的一个安装包，有图形界面，直接安装就能使用，安装完成后会自行下载两个基础的模型大概几个G。

在 8GB M1 MacBook Air 上，DiffusionBee 生成图像大约需要 30 秒。DiffusionBee 需在 macOS 12.5.1以上版本才能安装使用。

下载地址：

夸克网盘下载链接：https://pan.quark.cn/s/93e00229014e

二、魔法与巫术课程标准书籍

简单介绍

与B站大神秋葉aaaki的整合包一样，这个魔法与巫术课程标准书籍也是一个整合安装包，打开界面如何操作一目了然。

1、安装WEBUI；

2、一键启动；

下载地址：

夸克网盘下载链接：https://pan.quark.cn/s/ca7b9d428492

阅读原文，获取更多相关网盘资源，下载更方便：https://y3if3fk7ce.feishu.cn/docx/AJSEdVOBOoCUvYxpkwxcW2E8nfe

相关文章：

苹果MacOS系统傻瓜式本地部署AI绘画Stable Diffusion教程

Stable Diffusion的部署对小白来说非常麻烦，特别是又不懂技术的人。今天分享两个一键傻瓜式安装包，对小白来说非常有用。下面两个任选一个安装就可以。 一、DiffusionBee 简单介绍 DiffusionBee是基于stable diffusion的一个安装包，有图形…...

编程日记 2023/6/9 15:44:39

DBA之路-- 闪回恢复区FRA（Flash recovery area）与闪回特性（flashback)[待更新]

闪回恢复区FRA（Flash recovery area）与闪回特性（flashback） 1、闪回特性FB 用于快速简单恢复数据库中出现的认为误操作等逻辑错误 Flashback由undo表空间的撤销段内容为基础，受限于UNDO_RETENTON参数。要使用flashb…...

编程日记 2023/6/9 15:39:37

chatgpt赋能python：Python3.6.5到Python3.7.5：升级指南

Python 3.6.5到Python 3.7.5：升级指南 Python是一种广泛使用的编程语言，拥有强大的库和框架，能够开发各种类型的应用程序。在Python的发行版中，版本更新是常见的过程，以提供更好的性能和新的功能。 本文将介绍如何将…...

编程日记 2023/6/9 15:34:36

Element UI DatePicker 日期选择器

该组件选择周的时候，默认显示‘xxxx年第x周’，但在需求要显示为‘xxxx年x月第x周（mm.dd - mm.dd)’或者‘本周（mm.dd - mm.dd)’，最终效果为 首先需要修改v-model默认展示日期，控件中默认展示为周二&#x…...

编程日记 2023/6/9 15:29:35

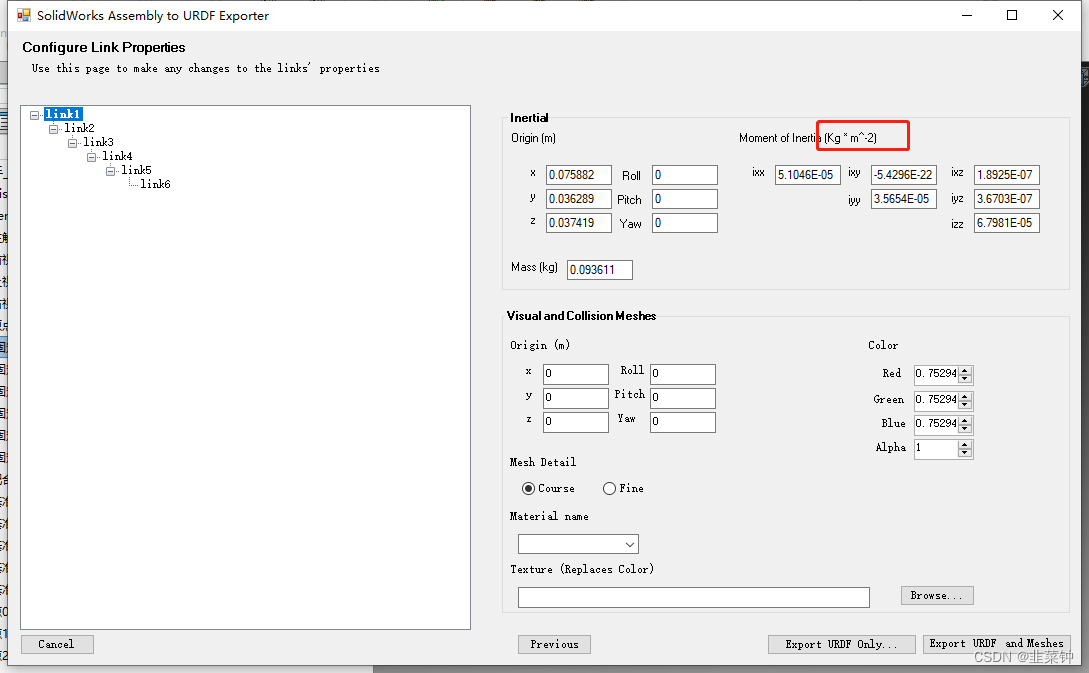
sw2urdf导出的urdf文件中的惯性参数（inertial）错误的问题

现象描述 有时候，当我们使用solidworks建好我们的模型，然后利用【sw2urdf】导出后，发现其中的惯性参数，似乎不正确，ixx、izz这些参数都是很接近0的： 资料查找 其实这个不是我们设置的问题，而…...

编程日记 2023/6/9 15:24:33

AICG - Stable Diffusion 学习思考踩坑实录（待续补充）

关于模型 如果模型中没有各种角度的脚和手，无论你再怎么费劲心思，AI 都画不出来，目前C 站也没有什么好脚的例子，正面脚背面脚，但是没有侧面脚，脚这块还是很欠缺，希望未来有大牛能训练出来美脚 …...

编程日记 2023/6/9 15:19:30

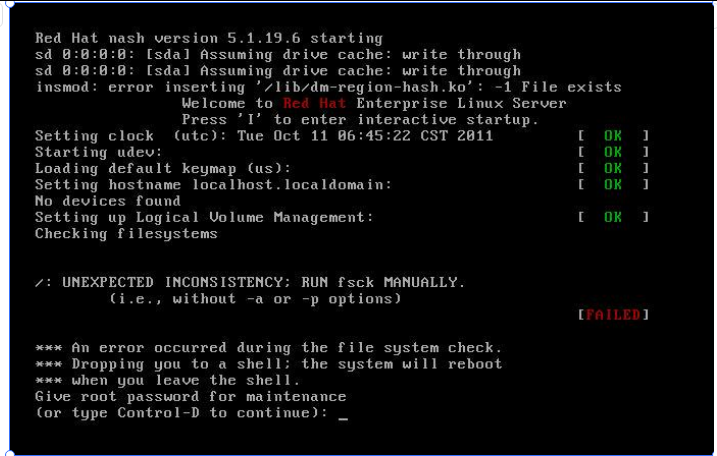
LiangGaRy-学习笔记-Day19

1、回顾知识 1.1、文件系统说明 xfs与ext4文件系统 CentOS7以上：默认的就是XFS文件系统 xfs 使用的就是restore、dump等工具 CentOS6默认的就是ext4文件系统 extundelete工具就是用于ext4系统 1.2、回顾Linux文件系统 Linux文件系统是由三个部分组成 inode文…...

编程日记 2023/6/9 15:14:29

智能指针（1）

智能指针（1） 概念内存泄漏指针指针概念RAII使用裸指针存在的问题 智能指针使用分类unique（唯一性智能指针）介绍智能指针的仿写代码理解删除器 概念 内存泄漏 内存泄漏：程序中已动态分配的堆内存由于某些原因而未释放…...

编程日记 2023/6/9 15:09:25

Steemit 会颠覆 Quora/知乎 甚至 Facebook 吗？

Steemit是基于区块链技术的社交媒体平台，其独特的激励机制吸引了众多用户。然而，是否能够真正颠覆Quora、知乎甚至Facebook这些已经成为社交巨头的平台，仍然存在着许多未知因素。本文将探讨Steemit的优势和挑战，以及其在社交领域中…...

编程日记 2023/6/9 15:04:24

002Mybatis初始化引入

引入依赖 <dependency><groupId>org.mybatis.spring.boot</groupId><artifactId>mybatis-spring-boot-starter</artifactId> </dependency> 自动检测工程中的DataSource创建并注册SqlSessionFactory实例创建并注册SqlSessionTemplate实例自…...

编程日记 2023/6/9 14:59:22

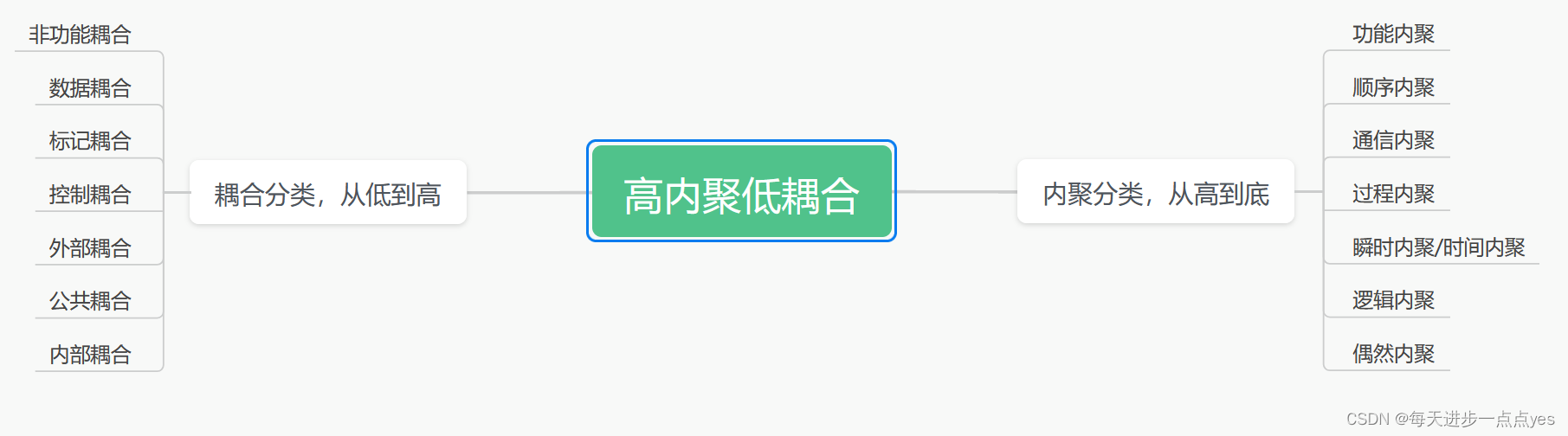
系统架构师之高内聚低耦合

一、概念&#xff1a; 标记耦合&#xff08;Stamp Coupling&#xff09;和数据耦合&#xff08;Data Coupling&#xff09;是软件设计中两种不同的耦合类型&#xff0c;它们之间的区别如下&#xff1a; 标记耦合&#xff1a;标记耦合是指模块之间通过参数传递标记或标识符来进…...

编程日记 2023/6/9 14:54:20

Netty核心源码剖析(二)

1.Netty接受请求过程源码剖析 1>.从之前的Netty启动过程源码剖析中,我们得知服务器最终注册了一个Accept事件等待客户端的连接.我们也知道,NioServerSocketChannel将自己注册到了bossGroup单例线程池(reactor线程)上,也就是EventLoop; 2>.先简单说下EventLoop的逻辑,Ev…...

编程日记 2023/6/9 14:49:19

「C/C++」C/C++ Lamada表达式

✨博客主页&#xff1a;何曾参静谧的博客 &#x1f4cc;文章专栏&#xff1a;「C/C」C/C程序设计 相关术语 Lambda表达式&#xff1a;是C11引入的一种函数对象&#xff0c;可以方便地创建匿名函数。与传统的函数不同&#xff0c;Lambda表达式可以在定义时直接嵌入代码&#xff…...

编程日记 2023/6/9 14:44:18

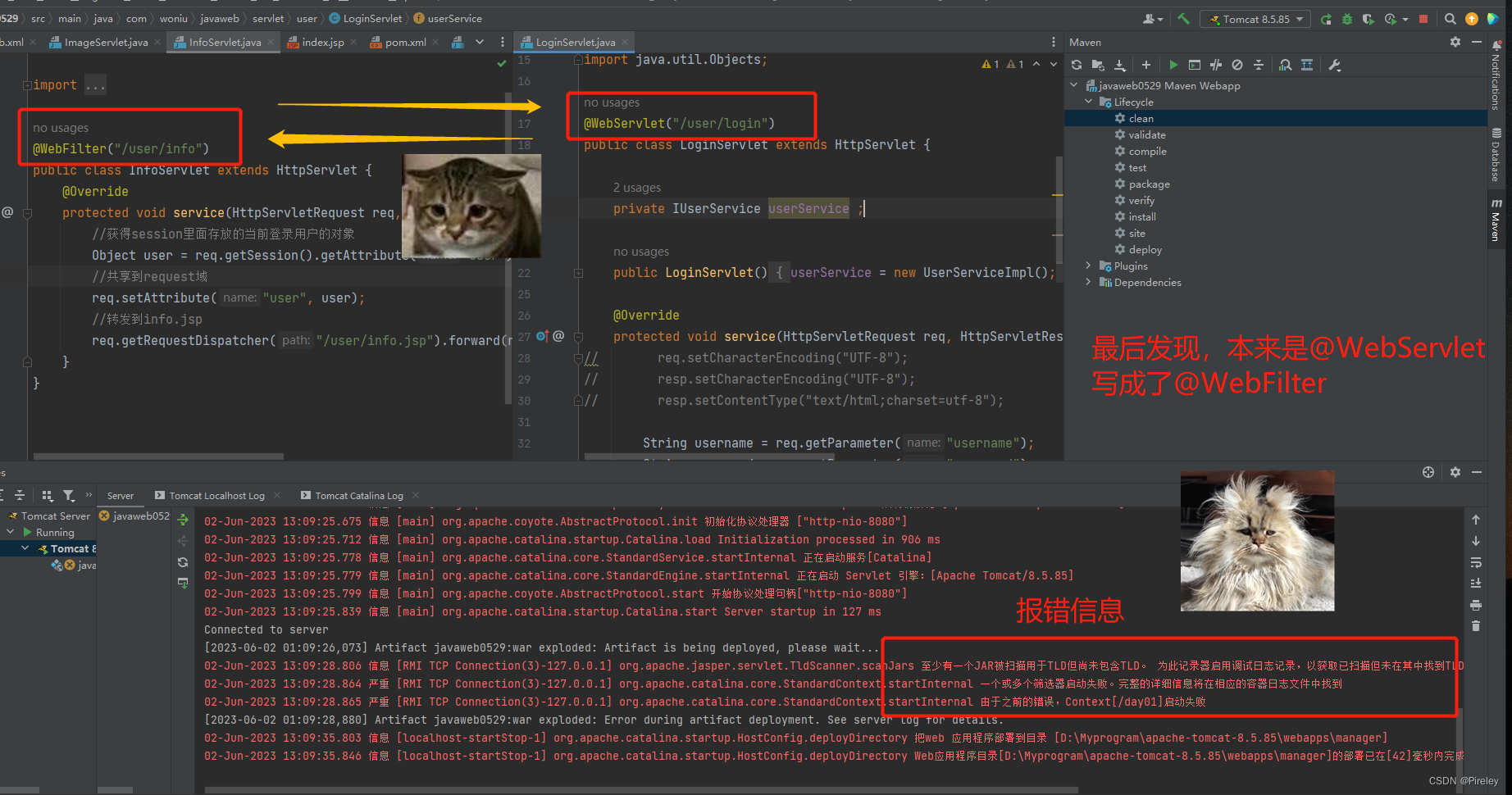
bug（Tomcat）：StandardContext.startInternal 由于之前的错误，Context[/day01]启动失败

引出 项目启动失败&#xff0c;一个困扰了一上午的bug 报错信息 org.apache.catalina.core.StandardContext.startInternal 一个或多个筛选器启动失败。完整的详细信息将在相应的容器日志文件中找到 org.apache.catalina.core.StandardContext.startInternal 由于之前的错误…...

编程日记 2023/6/9 14:39:17

Java性能权威指南-总结6

Java性能权威指南-总结6 垃圾收集入门垃圾收集概述GC算法选择GC算法 垃圾收集入门 垃圾收集概述 GC算法 JVM提供了以下四种不同的垃圾收集算法: Serial垃圾收集器 Serial垃圾收集器是四种垃圾收集器中最简单的一种。如果应用运行在Client型虚拟机(Windows平台上的32位JVM或…...

编程日记 2023/6/9 14:34:14

群的定义及性质

群的定义 设 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩为独异点&#xff0c;若 G G G中每个元素关于 ⋅ \cdot ⋅都是可逆的&#xff0c;则称 < G , ⋅ > \left<G,\cdot\right> ⟨G,⋅⟩为群 由于群中结合律成立&#xff0c;每个元素的逆元是唯一的 …...

编程日记 2023/6/9 14:29:13

mac电脑git clone项目时报错证书过期和权限被拒绝

mac电脑使用git clone命令克隆项目时&#xff0c;一开始一直提示证书过期 SSL certificate problem: certificate has expired 执行以下代码关掉验证后&#xff0c;解决了这个问题 找到git目录 Git\git-cmd输入命令跳转到bin目录&#xff0c;cd bin输入命令运行git.exe执行关…...

编程日记 2023/6/9 14:24:12

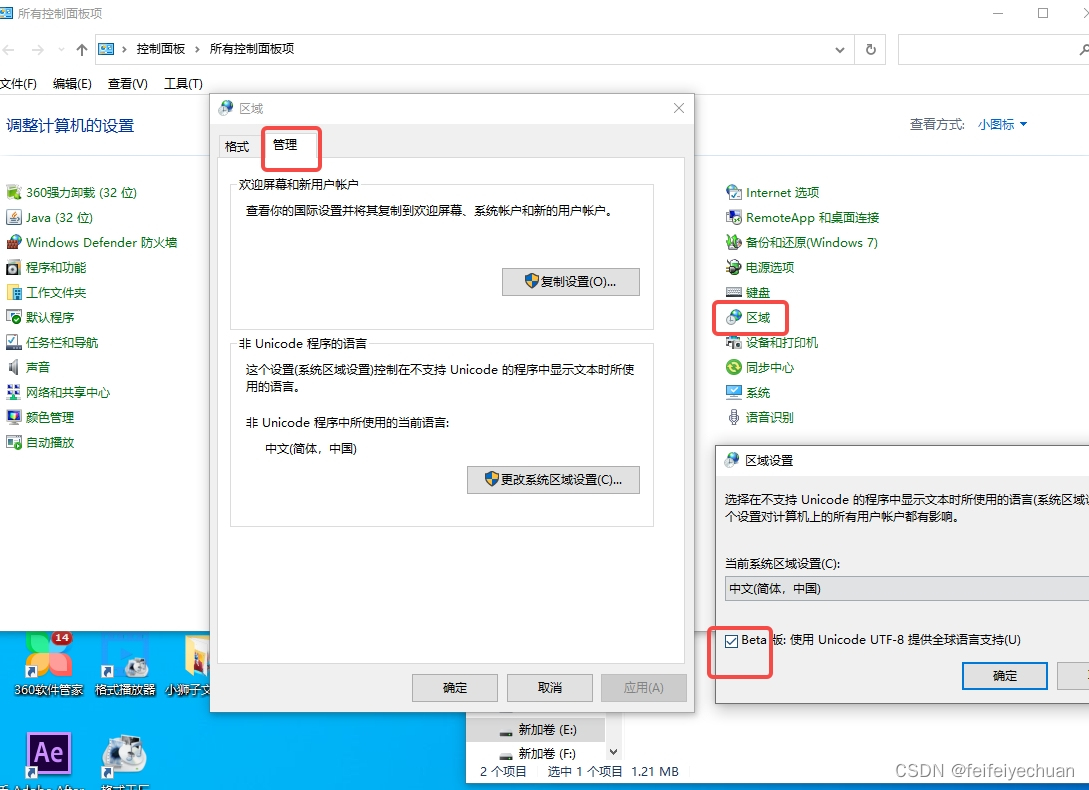
【AIGC】Photoshop AI Beta版本安装使用（永久免费）

AIGC 大爆发 Adobe近日宣布&#xff0c;Photoshop&#xff08;测试版&#xff09;应用程序发布了生成式AI绘图&#xff0c;这是世界上第一个创意和设计工作流程的副驾驶&#xff0c;为用户提供了一种神奇的新工作方式。生成式AI绘图由Adobe Firefly提供支持&#xff0c;Adobe的…...

编程日记 2023/6/9 14:19:10

01 云原生生态系统解读

云计算的技术革命 互联网时代的历程 云计算到底是什么 云计算历程 云平台的优缺点 优势 稳定性&#xff1a;云平台大量资源&#xff0c;分布式集群部署&#xff0c;保障服务永不宕机&#xff0c;几个9弹性扩展&#xff1a;按需索取&#xff0c;一键秒级开通需要的资源安全性&…...

编程日记 2023/6/9 14:14:10

Java——Java易错选择题复习（2）（计算机网络）

1. 下面关于源端口地址和目标端口地址的描述中&#xff0c;正确的是&#xff08; &#xff09; A. 在TCP/UDP传输段中&#xff0c;源端口地址和目的端口地址是不能相同的 B. 在TCP/UDP传输段中&#xff0c;源端口地址和目的端口地址必须是相同的 C. 在TCP/UDP传输段中&#xff…...

编程日记 2023/6/9 14:09:06

从WWDC看苹果产品发展的规律

WWDC 是苹果公司一年一度面向全球开发者的盛会&#xff0c;其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具&#xff0c;对过去十年 WWDC 主题演讲内容进行了系统化分析&#xff0c;形成了这份…...

编程新知 2026/2/2 21:52:33

PHP和Node.js哪个更爽?

先说结论&#xff0c;rust完胜。 php&#xff1a;laravel&#xff0c;swoole&#xff0c;webman&#xff0c;最开始在苏宁的时候写了几年php&#xff0c;当时觉得php真的是世界上最好的语言&#xff0c;因为当初活在舒适圈里&#xff0c;不愿意跳出来&#xff0c;就好比当初活在…...

编程新知 2025/9/14 7:59:52

Java如何权衡是使用无序的数组还是有序的数组

在 Java 中，选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南： ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

编程新知 2025/8/3 11:17:37

Objective-C常用命名规范总结

【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名&#xff08;Class Name)2.协议名&#xff08;Protocol Name)3.方法名&#xff08;Method Name)4.属性名&#xff08;Property Name&#xff09;5.局部变量/实例变量&#xff08;Local / Instance Variables&…...

编程新知 2025/12/14 22:33:06

CentOS下的分布式内存计算Spark环境部署

一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架&#xff0c;相比 MapReduce 具有以下核心优势&#xff1a; 内存计算&#xff1a;数据可常驻内存&#xff0c;迭代计算性能提升 10-100 倍&#xff08;文档段落&#xff1a;3-79…...

编程新知 2026/2/5 1:30:05

家政维修平台实战20：权限设计

目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系&#xff0c;主要是分成几个表&#xff0c;用户表我们是记录用户的基础信息&#xff0c;包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题&#xff0c;不同的角色&#xf…...

编程新知 2026/2/1 22:23:58

如何在最短时间内提升打ctf（web)的水平？

刚刚刷完2遍 bugku 的 web 题&#xff0c;前来答题。 每个人对刷题理解是不同&#xff0c;有的人是看了writeup就等于刷了&#xff0c;有的人是收藏了writeup就等于刷了&#xff0c;有的人是跟着writeup做了一遍就等于刷了&#xff0c;还有的人是独立思考做了一遍就等于刷了。…...

编程新知 2026/1/28 5:55:15

今日学习：Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存

文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

编程新知 2026/1/27 16:41:02

力扣-35.搜索插入位置

题目描述 给定一个排序数组和一个目标值&#xff0c;在数组中找到目标值&#xff0c;并返回其索引。如果目标值不存在于数组中&#xff0c;返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

编程新知 2025/12/3 3:22:43

Redis的发布订阅模式与专业的 MQ（如 Kafka, RabbitMQ）相比，优缺点是什么？适用于哪些场景？

Redis 的发布订阅&#xff08;Pub/Sub&#xff09;模式与专业的 MQ&#xff08;Message Queue&#xff09;如 Kafka、RabbitMQ 进行比较&#xff0c;核心的权衡点在于&#xff1a;简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

编程新知 2025/12/4 2:32:37