【学习笔记】[AGC048D] Pocky Game
这是一个非平等博弈。但是只要求你判断胜负,本身也不是一道结论题,所以可以用 D P DP DP来解决。
结论:第一堆石子剩的越多,先手玩家获胜的概率越大。这直接引出了一个非常感性的结论:每次取石子时要么取一堆,要么只取一个。很难理性证明这个博弈策略是正确的,但是博弈本身就是很玄学的东西,似乎我们找不出来一套普适的理论去判断游戏的胜负。那么只要这个策略本身具有合理性就可以采纳。就这道题而言,取一堆石子可以看成是加快游戏进度,取一个石子可以看成是让游戏的步数延长。看来这道题当中游戏步数是非常重要的维度,我们可以通过比较游戏步数的大小来判定胜负。
然后就是编 D P DP DP状态。设 f l , r f_{l,r} fl,r表示剩 [ l + 1 , r ] [l+1,r] [l+1,r]堆中石子时先手获胜, a l a_l al的最小数目, g l , r g_{l,r} gl,r表示剩 [ l , r − 1 ] [l,r-1] [l,r−1]堆中石子时后手获胜(后手先操作), a r a_r ar的最小数目。注意,这里我们要求 [ l , r ] [l,r] [l,r]中的石子堆都非空。这个状态给我一种 border \text{border} border的感觉,也就是要么左端点被截断或者右端点被截断,正好就是对应左右两端中两堆石子被消耗的过程。
接着编具体的转移。其实并不复杂:如果 g l + 1 , r > a r g_{l+1,r}>a_r gl+1,r>ar那么直接将第 l l l堆取空就行,有 f l , r = 1 f_{l,r}=1 fl,r=1;否则先手一定是消耗,并且 a l > 1 a_l>1 al>1,任意时刻如果 a l < f l , r − 1 a_l<f_{l,r-1} al<fl,r−1那么后手就会将第 r r r堆取完,从而先手必败,那么分类讨论:
1.1 1.1 1.1 如果 g l + 1 , r = 1 g_{l+1,r}=1 gl+1,r=1,那么一定要是后手取完,并且此时 a l a_l al恰好为 f l , r − 1 f_{l,r-1} fl,r−1,有 f l , r = f l , r − 1 + a r f_{l,r}=f_{l,r-1}+a_r fl,r=fl,r−1+ar
1.2 1.2 1.2 如果 g l + 1 , r ≠ 1 g_{l+1,r}\ne 1 gl+1,r=1,那么当 a l = f l , r − 1 a_l=f_{l,r-1} al=fl,r−1时第 r r r堆也恰好为 g l + 1 , r − 1 g_{l+1,r}-1 gl+1,r−1,此时再将 a l a_l al取完就变成先手必胜了,有 f l , r = f l , r − 1 + a r − g l + 1 , r + 1 f_{l,r}=f_{l,r-1}+a_r-g_{l+1,r}+1 fl,r=fl,r−1+ar−gl+1,r+1。
后手和先手是对称的就不说了。这个 D P DP DP转移还挺容易推错的,可能主要是因为没有想到临界时两端的石子数目都不为 0 0 0。
复杂度 O ( n 2 ) O(n^2) O(n2)。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define db double
using namespace std;
int T,n;
ll a[105],f[105][105],g[105][105];
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];memset(f,0x3f,sizeof f),memset(g,0x3f,sizeof g);for(int i=1;i<=n;i++){f[i][i]=1,g[i][i]=1;}for(int len=2;len<=n;len++){for(int l=1;l<=n-len+1;l++){int r=l+len-1;if(g[l+1][r]>a[r])f[l][r]=1;else f[l][r]=f[l][r-1]+a[r]-g[l+1][r]+1;if(f[l][r-1]>a[l])g[l][r]=1;else g[l][r]=g[l+1][r]+a[l]-f[l][r-1]+1;}}if(n==1||f[1][n]<=a[1]){cout<<"First"<<"\n";}else{cout<<"Second"<<"\n";}}
}相关文章:

【学习笔记】[AGC048D] Pocky Game
这是一个非平等博弈。但是只要求你判断胜负,本身也不是一道结论题,所以可以用 D P DP DP来解决。 结论:第一堆石子剩的越多,先手玩家获胜的概率越大。这直接引出了一个非常感性的结论:每次取石子时要么取一堆…...
Qgis中进行Shp和Excel属性连接实现百强县公共预算空间分析
前言 在之前的博文中,将2022的全国百强县一般公共预算收入的数据下载到了本地,博客原文地址:一种使用Java的快速将Web中表格转换成Excel的方法。对于不关注时空位置关系的一般分析,到此也就基本够用了。但是,如果站在全…...

ES6 新增的循环方法
在 ES6(ECMAScript 2015)中,新增了一些循环方法,这些方法可以帮助我们更方便地遍历数组、字符串、Set、Map 等数据结构。本文将介绍一些常用的 ES6 循环方法。 for…of 循环 for…of 循环是一种遍历可迭代对象的方法,…...

移动端事件300ms延迟解决
有移动端与PC端的项目开发,那么移动端和PC端开发上是存在差异的,比如 click 事件的300ms 延迟,即移动Web页面上的click事件响应都要慢上300ms,移动设备访问Web页面时往往需要 “双击” 或者 “捏开” 来放大页面看清页面的具体内容…...
NRF52832的DFU
开发环境: Winsodw:10 nRF5_SDK:17.1.0 1 工具安装 1.1 gcc-arm-none-eabi Downloads | GNU Arm Embedded Toolchain Downloads – Arm Developer 下载“gcc-arm-none-eabi-10.3-2021.10-win32.exe”,接提示安装。注意安装完…...
开源WebRTC库放大器模式在采集桌面图像时遇到的DPI缩放与内存泄漏问题排查
目录 1、在非100%的显示比例下放大器采集到的桌面图像不全问题 1.1、通过manifest文件禁止系统对软件进行缩放 1.2、调用SetThreadDpiAwarenessContext函数,禁止系统对目标线程中的窗口进行缩放 1.3、使用winver命令查看Windows的年月版本 2、使用放大器模式遇…...

敲黑板!java反射机制和原理
获取Class对象:首先,你需要获取表示要操作的类的Class对象。可以使用以下三种方式之一来获取Class对象: Class.forName()方法:使用类的全限定名获取Class对象,例如:Class<? Class<?> clazz MyC…...
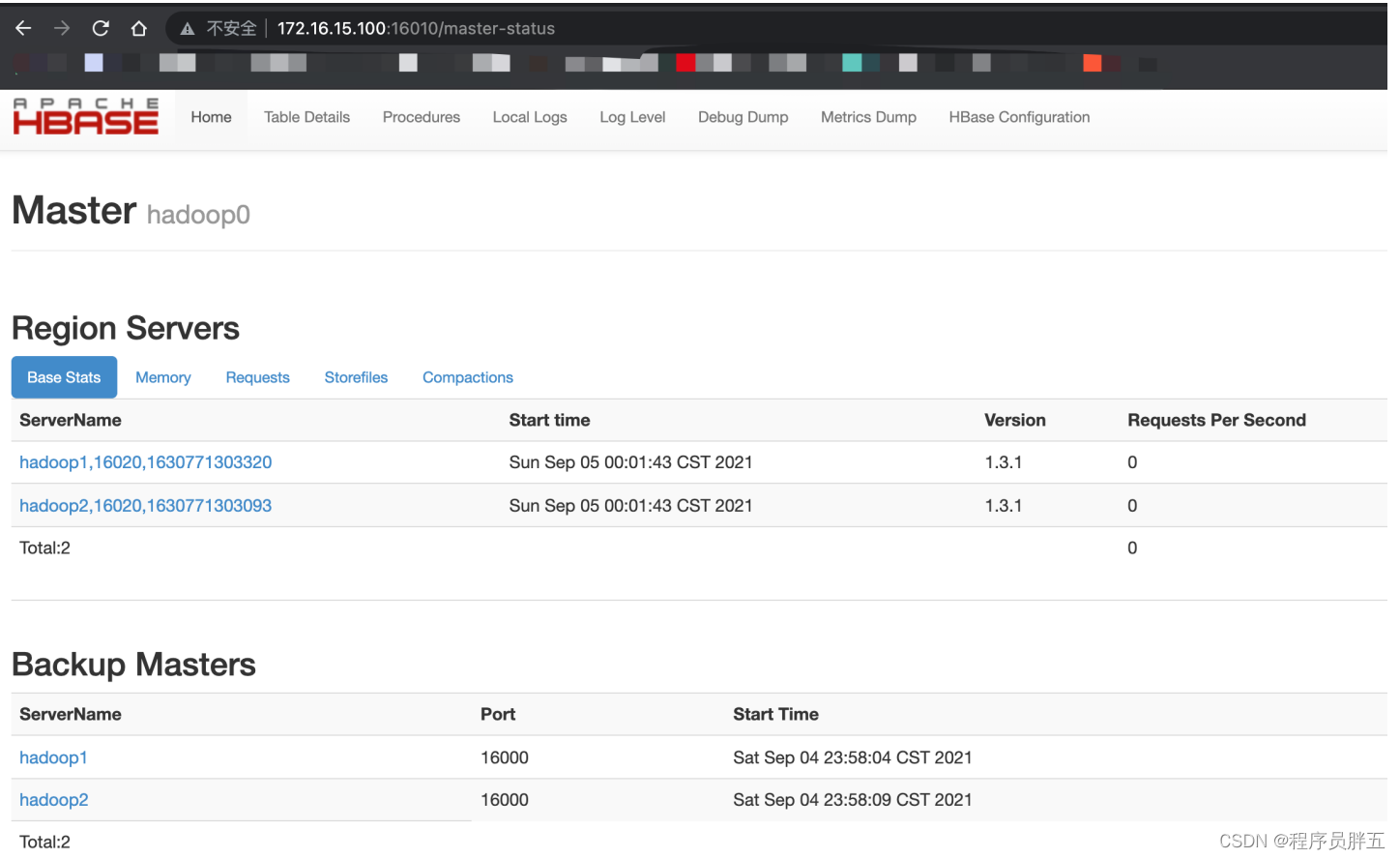
【大数据工具】HBase 集群搭建与基本使用
HBase 集群搭建 HBase 安装包下载地址:https://archive.apache.org/dist/hbase/ 安装 HBase 的前提: ZooKeeper 集群 OKHadoop 集群 OK 1. HBase 集群安装 1. 将 HBase 软件包上传至 Hadoop0 解压并重命名 使用 FileZilla 将 hbase-1.3.1-bin.tar.g…...
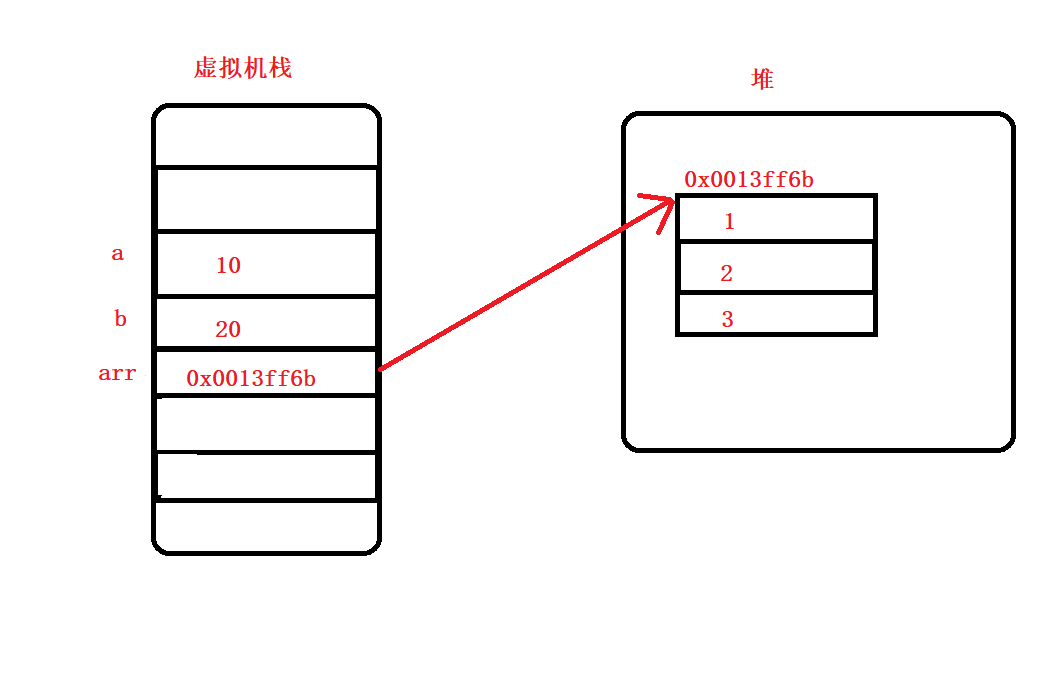
【Java】数组详解
文章目录 一、数组的基本认识1.1 数组的概念1.2数组的创建与初始化1.3 数组的使用 二、数组的类型 — 引用类型2.1 JVM 内存分布2.2 什么是引用类型2.3 基本类型变量与引用类型变量的区别2.4 Java 中的 null 三、数组的应用3.1 保存数据3.2 函数参数3.3 函数返回值 一、数组的基…...
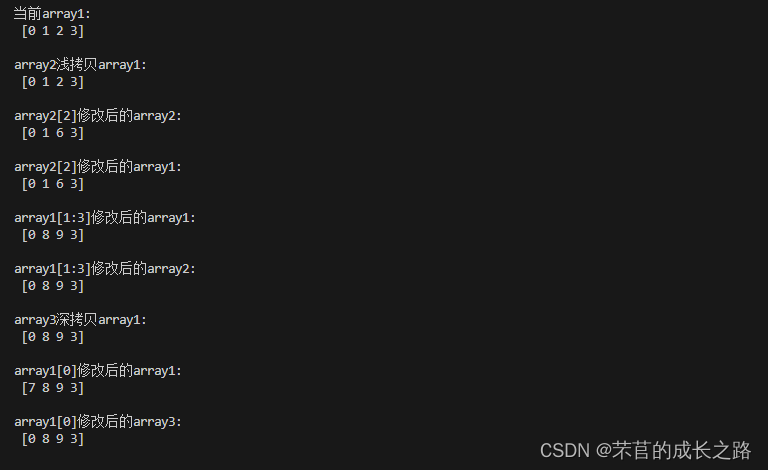
NumPy库的学习
本文主要记录的是笔者在B站自学Numpy库的学习笔记。 引入numpy库 import numpy as np矩阵的创建 创建一个二行三列的矩阵。 array np.array([[1,2,3],[2,3,4]])查看array的行数、形状、元素数量 print("number of dim:",array.ndim) print("shape:"…...

CentOS安装IRIS
最近电脑提搞了,可以无顾虑创建虚拟机了,试一下在Linux安装IRIS,适用CentOS7.6上安装Intersystem公司的IRIS数据库,资料基本是空白,分享一下。 首先安装解压软件unzip和libicu,最小化安装的缺,…...

华为OD机试真题 JavaScript 实现【最多几个直角三角形】【2023Q1 100分】
一、题目描述 有 N 条线段,长度分别为 a[1]-a[n]。 现要求你计算这 N 条线段最多可以组合成几个直角三角形,每条线段只能使用一次,每个三角形包含三条线段。 二、输入描述 第一行输入一个正整数 T (1< T< 100) ,表示有…...

vue3中的reactive、ref、toRef和toRefs
目录 reactivereactive的实现原理使用reactive的注意事项 refref的实现原理使用ref的注意事项 toRef和toRefsref和reactive的使用比较 reactive reactive用于创建响应式对象,它返回一个对象的响应式代理。即:它返回的对象以及其中嵌套的对象都会通过 Pr…...

数字图像处理与Python实现-图像增强经典算法汇总
图像增强经典算法汇总 文章目录 图像增强经典算法汇总1、像素变换2、图像逆变换3、幂律变换4、对数变换5、图像均衡化6、对比度受限自适应直方图均衡(CLAHE)7、对比度拉伸8、Sigmoid校正9、局部对比度归一化10、总结本文将对图像增强经典算法做一个简单的汇总。图像增强的经典…...

tag提示词总结
顺序的权重 越靠前的tag权重越大,越靠后的tag权重越小经验来讲,将图像质量相关的tag放在前面,例如masterpiece,best quality等;接着添加主体画风等;最后添加一些不太重要的细节 权重增减 (tag):…...

微信小程序原生开发功能合集二十:导航栏、tabbar自定义及分包功能介绍
本章实现导航栏及tabbar的自定义处理的相关方法介绍及效果展示。 另外还提供小程序开发基础知识讲解课程,包括小程序开发基础知识、组件封装、常用接口组件使用及常用功能实现等内容,具体如下: 1. CSDN课程: https://edu.csdn.net/course/detail/37977 2. 5…...

高通 Camera HAL3:项目开发技术点总结
做高通 Camera HAL3开发的一些技术点的总结、整理。 做个记录,方便后续查阅。 1.目录、so、配置文件 productName是项目名 out Target路径:\out\target\product\productName\chi-cdk:\vendor\qcom\proprietary\chi-cdk\ldc node࿱…...

chatgpt赋能python:Python怎么删除列表中的最大值和最小值
Python怎么删除列表中的最大值和最小值 在Python中,一个列表(List)是一种非常常见的数据结构,它允许我们以有序的方式存储和访问数据。但是,有时候我们需要从列表中删除最大或最小的值,以满足我们的特定需…...

简述Vue的生命周期以及每个阶段做的事情
03_简述Vue的生命周期以及每个阶段做的事情 思路 给出概念 列举出生命周期各个阶段 阐述整体流程 结合实际 扩展:vue3变化 回答范例 每个vue组件实例被创建后都会经过一系列步骤。比如它需要数据观测、模板编译、挂载实例到dom、以及数据变化的时候更新dom、…...

LeetCode-C#-0004.寻找两个正序数组的中位数
0.声明 该题目来源于LeetCode 如有侵权,立马删除。 解法不唯一,如有新解法可一同讨论。 1.题目 0004寻找两个正序数组的中位数 给定两个大小分别为m和n的正序(从小到大)数组nums1和nums2。 请你找出并返回着两个正序数组的中位…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...
