基于前推回代法的连续潮流计算研究【IEEE33节点】(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
目前的配电网潮流计算方法主要有改进的牛顿 - 拉 夫 逊 法[1]、改 进 PQ 解 耦 法[2]、回 路 阻 抗法[3 - 4]、前推回代法[5 - 7]等。牛顿 - 拉夫逊法及改进 PQ 解耦法由于其自身原理的缺点,直接应用于配电网潮流计算时,收敛性较差且计算误差大。回路阻抗法主要应用于处理环网结构,收敛性较好,但其节点和支路编号处理复杂且计算量大。针对配电网辐射状结构的特点,前推回代法是配电网潮流计算最优算法之一,收敛性好且计算速度快。传统的前推回代法在计算前需要对网络的节点、支路进行预编号,可能导致计算错误,因此文献[5 - 6]提出了一种自动编号法,但该方法未考虑日益增加的分布式电源对配电网的影响。文献[7]指出传统前推 回代法的无功功率取值可能与实际值出入较大,将导致计算误差增大影响迭代结果,因此需要将 PV
节点转化为 PQ 节点,然后对无功和电压方程进行处理; 然而,将所有 PV 节点转化为 PQ 节点又会导致潮流计算收敛性变差。
各类配电网潮流算法性能通常从以下几个方面进行分析:
1) 算法的收敛速度。改进的牛顿 - 拉夫逊法将非线性的方程通过一定变换转化为对相应线性方
程的反复求解,且是二阶算法,具有平方收敛的特点,能在个位次数的迭代中迅速求解。
2) 稳定性。在配电网中,电力系统网络结构、线路参数及各种扰动因素对计算结果影响的程度即
为稳定性。由于牛顿拉夫逊算法是二阶算法,且受到配电网 R /X 比值较高的影响而无法输出准确的计算结果。而前推回代法受到的影响则很小。
3) 算法的复杂程度。用简单原理的算法通常更可靠,由于前推回代法不需要计算节点导纳矩阵,
其计算效率高。综上所述,前推回代法的原理更符合实际配电网结构的要求,其处理环网结构方面的能力较弱; 但配电网的主要特点就是运行时呈辐射状,因此并不会受到太大的影响。此外,该方法计算误差小、计算时间少,在系统异常时仍能保证输入有效结果,且收敛性能不会被配电网高 R /X 数值影响,目前已经广泛被用作计算配电网潮流的主要算法。
📚2 运行结果
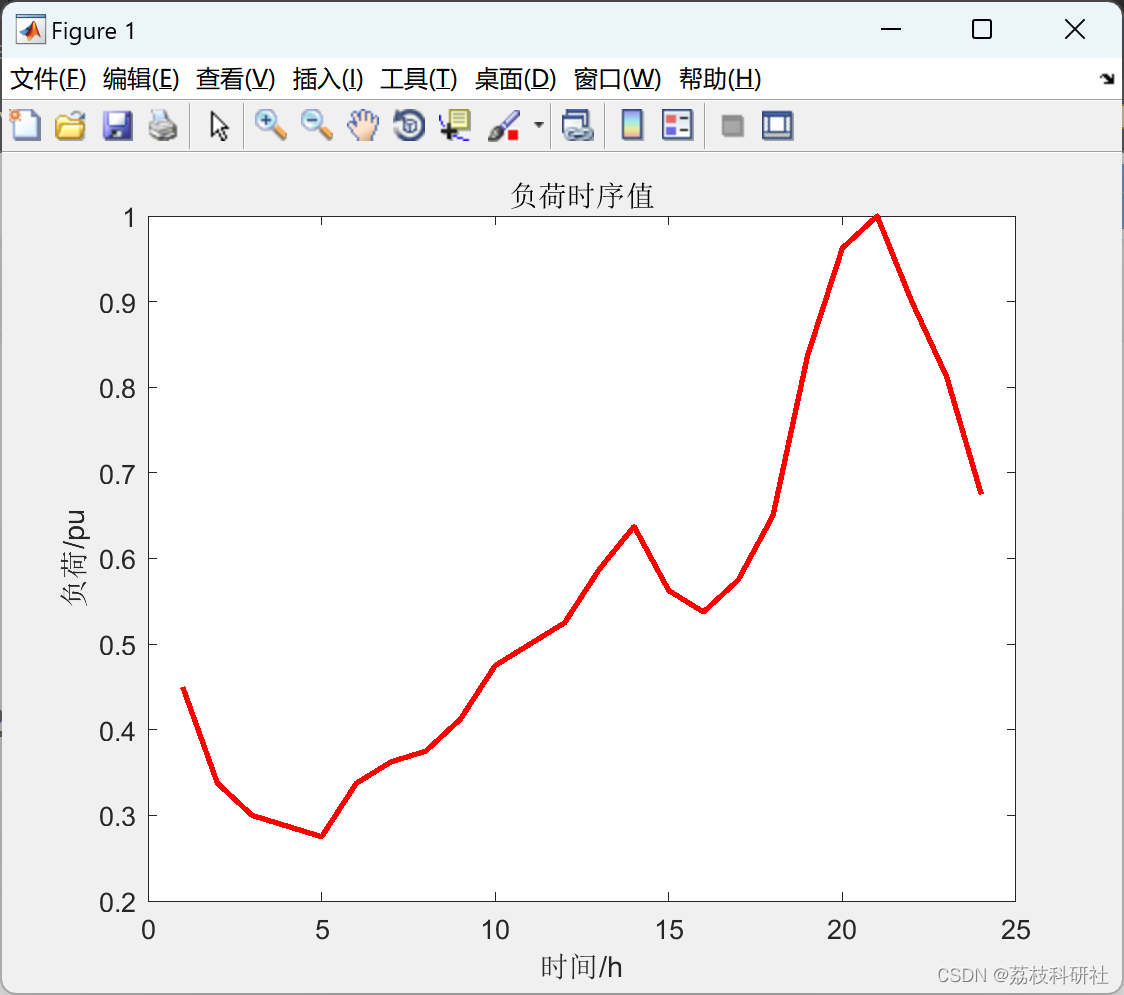
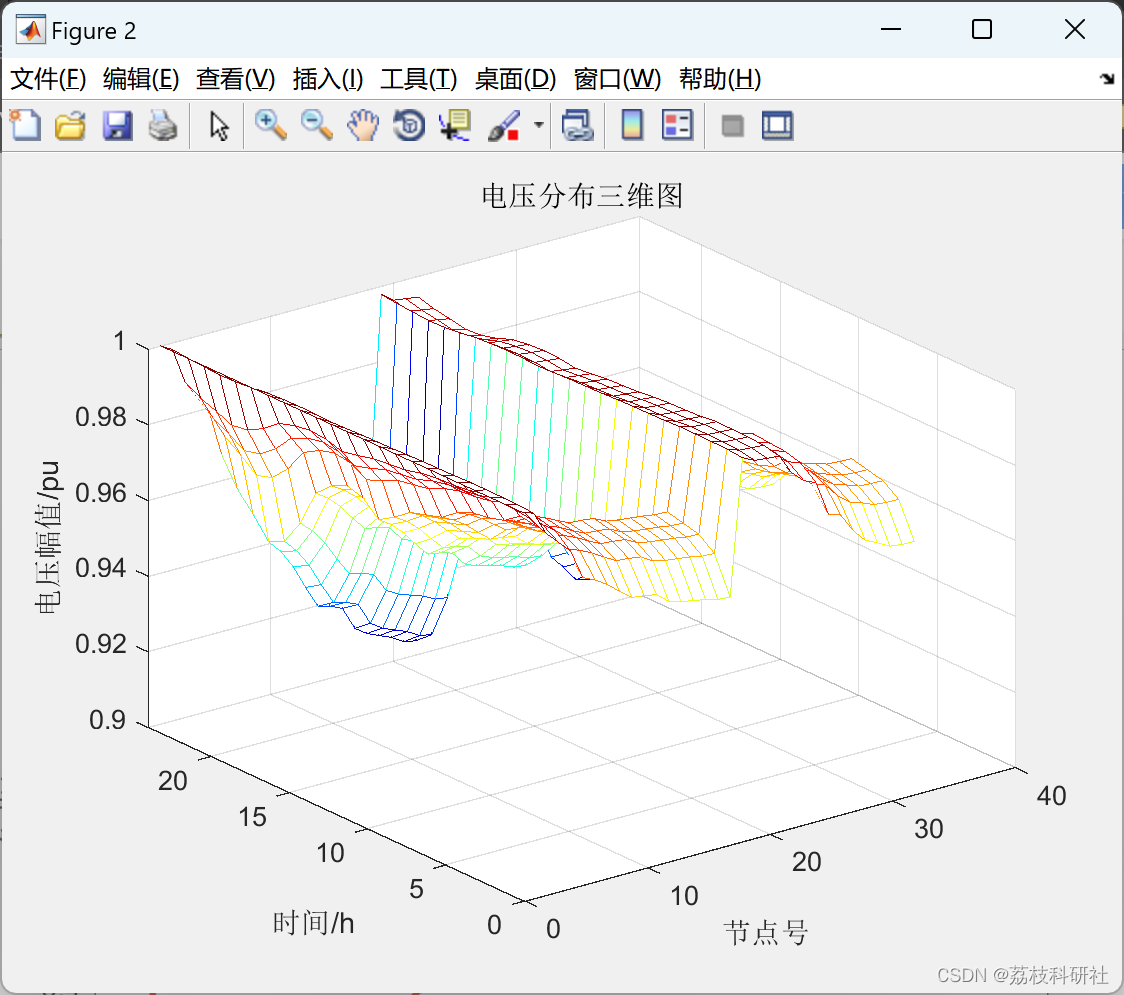
%% 系统支路参数 节点 节点 电阻 电抗
Branch=[1 ,1 ,2 ,0.0922,0.0407;
2 ,2 ,3 ,0.4930,0.2511;
3 ,3 ,4 ,0.3660,0.1864;
4 ,4 ,5 ,0.3811,0.1941;
5 ,5 ,6 ,0.8190,0.7070;
6 ,6 ,7 ,0.1872,0.6188;
7 ,7 ,8 ,0.7144,0.2351;
8 ,8 ,9 ,1.0300,0.7400;
9 ,9 ,10,1.0440,0.7400;
10,10,11,0.1966,0.065;
11,11,12,0.3744,0.1238;
12,12,13,1.4680,1.1550;
13,13,14,0.5416,0.7129;
14,14,15,0.5910,0.5260;
15,15,16,0.7463,0.5450;
16,16,17,1.2890,1.7210;
17,17,18,0.7320,0.5740;
18,2, 19,0.1640,0.1565;
19,19,20,1.5042,1.3554;
20,20,21,0.4095,0.4784;
21,21,22,0.7089,0.9373;
22,3, 23,0.4512,0.3083;
23,23,24,0.8980,0.7091;
24,24,25,0.8960,0.7011;
25,6, 26,0.2030,0.1034;
26,26,27,0.2842,0.1447;
27,27,28,1.0590,0.9337;
28,28,29,0.8042,0.7006;
29,29,30,0.5075,0.2585;
30,30,31,0.9744,0.9630;
31,31,32,0.3105,0.3619;
32,32,33,0.3410,0.5302;];
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]张捷,徐焰,张学飞.一种改进前推回代法的配电网潮流计算[J].四川电力技术,2020,43(03):85-90.DOI:10.16527/j.cnki.cn51-1315/tm.2020.03.017.
[2]张宾.基于改进Matpower连续潮流算法的静态电压稳定性分析[J].西安文理学院学报(自然科学版),2020,23(02):25-29.
[3]张小敏,林群,吴旭光,林振兴,杨惠源,唐爱红.适用于低压配电网潮流计算的前推回代法[J].水电能源科学,2016,34(09):183-186+70.
🌈4 Matlab代码实现
相关文章:

基于前推回代法的连续潮流计算研究【IEEE33节点】(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

【双向链表】
双向链表 带头双向循环链表的实现1. 函数的声明2. 函数的实现3. 主函数测试 带头双向循环链表的实现 今天我们来实现一下带头双向循环链表,顾名思义,带头就是有哨兵位,哨兵位不是链表的头,它是连接头节点的一个节点,方…...

POSTGRESQL NEON - Serverless 式的POSTGRESQL 数据库的独特技能 分支数据
开头还是介绍一下群,如果感兴趣polardb ,mongodb ,mysql ,postgresql ,redis 等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请联系 liuaustin3 ,在新加的朋友会分到2群(共…...

数据分布——长尾分布的处理
前言 长尾分布在分类任务中会提到这个名,这是因为长尾分布这个现象问题会导致在训练过程中会出现出错率高的问题,影响了实验结果。 这里要说的是,长尾分布是一种现象,有的地方说是一种理论或定律,我感觉这样说不太确切࿰…...
集合导题、刷题、考试全套完整流程,专业强大的功能,提高刷题学习效率和企业的培训效率
土著刷题微信小程序v1.15,主要是迭代了考试模块的进阶功能,对考试模块进行了一次升级改造。 由于在v1.15开发期间,收到了违规内容整改的通告,为了遵守相关法律法规,让小程序能够平稳安全地运营下去,我们特此…...
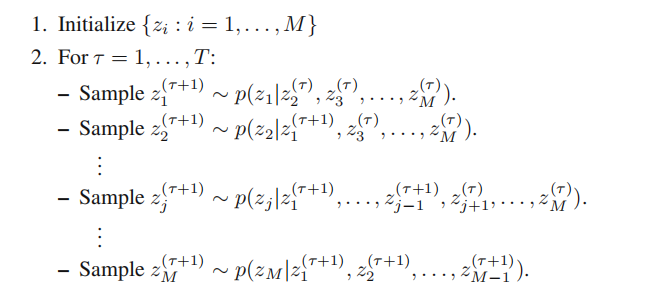
【机器学习】采样方法
文章目录 采样方法11.1 简介11.2 常见采样方法11.2.1 均匀分布采样11.2.2 逆变换采样11.2.3 拒绝采样11.2.4 重要采样11.2.5 Metropolis方法11.2.6 Metropolis-Hasting 算法11.2.7 吉布斯采样 采样方法 11.1 简介 什么是采样 从一个分布中生成一批服从该分布的样本,…...
Seata TCC 模式理论学习、生产级使用示例搭建及注意事项 | Spring Cloud55
一、前言 通过以下系列章节: docker-compose 实现Seata Server高可用部署 | Spring Cloud 51 Seata AT 模式理论学习、事务隔离及部分源码解析 | Spring Cloud 52 Spring Boot集成Seata利用AT模式分布式事务示例 | Spring Cloud 53 Seata XA 模式理论学习、使用…...

一文详解:Vue3中使用Vue Router
目录 安装和配置Vue Router安装Vue Router配置Vue Router Vue Router的基本概念Vue Router 的配置项介绍routes中的配置项介绍 路由跳转使用 router-link组件使用router.push函数 路由传参动态路由嵌套路由命名路由路由守卫全局路由守卫路由独享守卫 路由懒加载使用import()方式…...
C++开发—远程控制
C开发—远程控制 一,准备二,安装版本控制工具1,安装gitforwindows2,安装乌龟git1,安装乌龟git应用2,安装乌龟git对应的语言包 3,设置Visual Studio的git插件4,创建git项目 三&#x…...
)
【Python基础】Python数据容器(集合)
文章目录 数据容器:set(集合)集合的定义集合的常用操作-修改(1)添加新元素(2)移除元素(3)从集合中随机取出元素(4)清空集合(5)取出 两个集合的差集(6)消除 两个集合的差集(7)两个集合 合并(8)统计集合元素数量len()(9)集合的遍历 集合的特点 …...

高通 Camera HAL3:集成camxoverridesettings.txt到整机版本
camxoverridesettings.txt 是高通提供给开发者临时进行CAMX、CHI-CDK功能调试的一种方式,通过配置各种变量值然后写入到该文件,能控制Log打印、参数配置、数据dump等多种功能 这个文件需要集成在设备目录的vendor/etc/camera/里 因为camxoverridesetti…...

PHP面试题大全
一 、PHP基础部分 1、PHP语言的一大优势是跨平台,什么是跨平台? PHP的运行环境最优搭配为ApacheMySQLPHP,此运行环境可以在不同操作系统(例如windows、Linux等)上配置,不受操作系统的限制,所以…...

Linux发送接收邮件
目录 一、实验 1.linux用户发送给linux中的其它用户 2.linux用户发送给外网用户 一、实验 1.linux用户发送给linux中的其它用户 (1)使用命令 yum install -y sendmail 安装sendmail软件 (2)使用yum install -y mailx 安装 mail…...

SpringBoot-【回顾】
第一个SpringBoot程序 自动装配原理 Springboot的自动装配实际上就是为了从Spring.factories文件中获取到对应的需要进行自动装配的类,并生成相应的Bean对象,然后将它们交给Spring容器来帮我们进行管理 启动器:以starter为标记 EnableAuto…...
)
Python模拟试卷2023(1)
模拟试卷(1) 一、简答题 (共8题,100分) 1、已知有列表lst[54,36,75,28,50],请完成一下操作: 1、在列表尾部插入元素42 2、在元素28前面插入66 3、删除并输出28 4、将列表按降序排序 5、清空整个列表 lst[54,3…...

常量接口 vs 常量类 vs 枚举区别
把常量定义在接口里与类里都能通过编译,那2者到底有什么区别呢? 那个更合理? 常量接口 public interface ConstInterfaceA {public static final String CONST_A "aa";public static final String CONST_C "cc"; } 存在…...

第二章 模态命题:必然、可能
第二章 模态命题:必然、可能 第一节 模态命题-句式转换-逻辑转换 题-模态命题-句式转换-逻辑转换:①不一定不可能;②不一定可能不未必。 1.唐代韩愈在《师说》中指出:“孔子曰:三人行,则必有我师。是故…...

Selenium 必了解—如何测试REST API
目录 前言: Web UI测试存在的问题: REST API测试: 依赖包 程序示例: 1-获取联系人 2-GET Request: 3-POST Request: 4- 编辑请求 5- 删除请求 前言: Selenium WebDriver 可以用于测试 Web 应用的…...

pytorch安装老版本
比如1.7.1, cuda 10.1 pip install torch1.7.1cu101 -f https://download.pytorch.org/whl/torch_stable.html官网查看有哪些可以装的: https://download.pytorch.org/whl/torch_stable.html...

怎么自学电脑编程
首要之首:不要急于选择一种语言 新手们有一个常见的错误就是犹豫于判断哪种编程语言是做好的、最该先学的。 我们有很多的选择,但你不能说那种语言最好。 我们应该理解:说到底,什么语言并不重要。 重要的是理解数据结构、控制逻辑…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

