“Chain of Thought Reasoning“ 和 “Chain Prompts“ 是什么
"Chain of Thought Reasoning" 和 "Chain Prompts" 是什么
- 1. "Chain Prompts" 是什么
- 2. “Chain of Thought Reasoning” 是什么
1. “Chain Prompts” 是什么
“Chain Prompts” 是指一系列相关的提示,它们之间有逻辑上的联系和依赖关系。用户需要基于前一个提示的回答来回答后一个提示。
举个例子:
Prompt 1: 你最喜欢的书是什么?
用户回答:我最喜欢的书是《哈利波特》。
Prompt 2: 那你最喜欢《哈利波特》里的哪个人物?
用户回答:我最喜欢的人物是赫敏。
Prompt 3: 赫敏身上你最欣赏的品质是什么?
用户回答:我最欣赏赫敏的聪明和理性。
这个例子包含3个提示,它们之间有逻辑关联:
- 第一个提示问用户最喜欢的书,用户选择了《哈利波特》
- 第二个提示基于第一个提示的回答,问用户最喜欢的《哈利波特》人物,用户选择了赫敏
- 第三个提示基于第二个提示的回答,问用户最欣赏赫敏的什么品质
所以这3个提示构成了一个链条,每个后续提示都依赖前一个提示的回答。这就是 “Chain Prompts” 的意思和示例。
"Chain Prompts"可以让对话显得更加连贯和有逻辑,这是设计人机对话时常用的手法之一。
2. “Chain of Thought Reasoning” 是什么
“Chain of Thought Reasoning” 是指一种由一连串相关联的思维构成的推理过程。在这种推理过程中,一个思维可以触发下一个相关的思维,最终形成一条细致连贯的推理链。
举个例子:
思维1:我这个月的水电费明显高了许多。
思维2:最近天气比较热,空调开的时间长了,这可能是导致水电费上升的原因之一。
思维3:不过我家里这段时间人也比较多,房间也常开着电脑和电视,这也会增加用电量。
思维4:想想看,这两个月浴室也多次出过问题,修理工来过几次,水龙头和花洒可能也不太密合,这也会造成水资源的浪费从而提高水电费。
思维5:看来水电费的上升还是由多重因素造成的,不仅仅是Because天气问题那么简单。要想降低家庭开销,还需从多个方面着手。
这个例子展示了一个推理的过程,每个思维都与前一个思维有逻辑关联,最后形成了一条分析水电费上升原因的连贯推理链。这个就是 “Chain of Thought Reasoning” 的意思和示例。
利用 “Chain of Thought Reasoning”,我们可以进行更加深入全面与细致连贯的分析推理,这也常常出现在人与人的日常对话中。
完结!
相关文章:

“Chain of Thought Reasoning“ 和 “Chain Prompts“ 是什么
"Chain of Thought Reasoning" 和 "Chain Prompts" 是什么 1. "Chain Prompts" 是什么2. “Chain of Thought Reasoning” 是什么 1. “Chain Prompts” 是什么 “Chain Prompts” 是指一系列相关的提示,它们之间有逻辑上的联系和依赖关系。用户…...

signal
读信号,dqs 是对齐到dq的边沿, 写信号,dqs 的边沿是对到中间的。 spec 就是这样规定的。我们在dq的最中间的采样,肯定是最安全的。 dqs 是对齐到dq的边沿 , 在silicon 内部,还是通过移位完成的。 rl: re…...

深度研究微软的资产负债表和财务状况以及未来投资价值
来源:猛兽财经 作者:猛兽财经 微软股票的关键指标 猛兽财经认为,微软公布的2023财年第三季度财务业绩,有三个关键指标值得投资者关注。 第一个关键指标是利息收入。微软的利息收入目前已经同比增长了44%,从2022财年第…...
Mac电脑删除第三方软件工具CleanMyMac X
经常使用Mac的人都知道,Mac除了可以在AppStore下载应用程序,还有许多软件是需要在网页上搜索下载的第三方软件。那么这类第三方软件软件除了下载方式不同之外还有什么是和从App store下载的软件有区别的吗?答案是肯定的,那就是这些…...
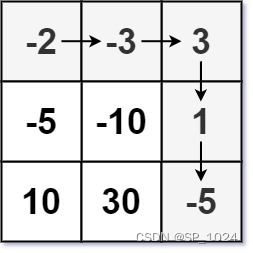
leetcode174. 地下城游戏(java)
地下城游戏 leetcode174. 地下城游戏题目描述 动态规划解题思路代码 动态规划专题 leetcode174. 地下城游戏 来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/dungeon-game 题目描述 恶魔们抓住了公主并将她关在了地下城 …...

信号与系统复习笔记——傅里叶变换
信号与系统复习笔记——傅里叶变换 周期信号的傅里叶级数表示 特征函数 假设LTI系统的输入为 x ( t ) e s t x(t) e^{st} x(t)est 输出为: y ( t ) e s t ∗ h ( t ) ∫ − ∞ ∞ e s ( t − τ ) h ( τ ) d τ e s t ∫ − ∞ ∞ e − s τ h ( τ ) d…...
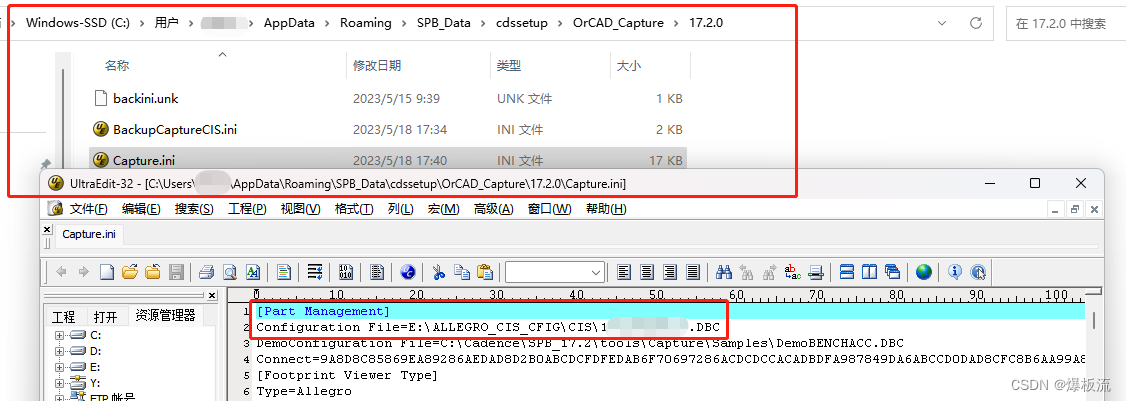
Allegor17.2版本WIN11系统CIS配置提示错误解决方案
错误提示: ERROR(ORCIS-6250): Unable to continue. Database access failed. Contact the database administrator to correct the following error(s), and then retry. ODBC Error Code: -1 Description: 在指定的 DSN 中,驱动程序和应用程序之间的体…...

Java设计模式七大原则-合成聚合复用原则
🧑💻作者:猫十二懿 ❤️🔥账号:CSDN 、掘金 、个人博客 、Github 🎉公众号:猫十二懿 合成-聚合复用原则 1、合成-聚合复用原则介绍 合成/聚合复用原则(Composition/Aggregatio…...

SOFA Weekly|可信基础设施技术分论坛、Layotto 社区会议回顾与预告、社区本周贡献...
SOFA WEEKLY | 每周精选 筛选每周精华问答,同步开源进展 欢迎留言互动~ SOFAStack(Scalable Open Financial Architecture Stack)是蚂蚁集团自主研发的金融级云原生架构,包含了构建金融级云原生架构所需的各个组件&am…...

Melody 监控(四十九)
当新的世界出现,请立即向他奔去 上一章简单介绍了Spring Boot Actuator详解(四十八), 如果没有看过,请观看上一章 一. JavaMelody 一.一 什么是 Java Melody JavaMelody是一个方便的Java或JavaEE Web 应用程序监控工具。 它允许自动存储由 Web 应用程序的实际操…...

Shell脚本管道符常用搭配命令
1.sort sort命令——以行为单位对文件内容进行排序,也可以根据不同的数据类型来排序比较原则是从首字符向后,依次按ASCII码值进行比较,最后将他们按升序输出。 sort [选项] 文件名 cat file | sort [选项] 常用选项 选项作用-n按照数字进行…...
基于html+mysql+Spring+mybatis+Springboot的Springboot宠物医院管理系统
运行环境: 最好是java jdk 1.8,我在这个平台上运行的。其他版本理论上也可以。 IDE环境: Eclipse,Myeclipse,IDEA或者Spring Tool Suite都可以,如果编译器的版本太低,需要升级下编译器,不要弄太低的版本 tomcat服务器环…...
:搜索(5):其他)
算法模板(3):搜索(5):其他
搜索 模拟退火 模拟退火一个很关键的是,看看枚举到每一个方案是不是可能的。 3167. 星星还是树 在二维平面上有 n 个点,第 i 个点的坐标为 ( x i , y i ) (x_i,y_i) (xi,yi)。请你找出一个点,使得该点到这 n 个点的距离之和最小。这…...
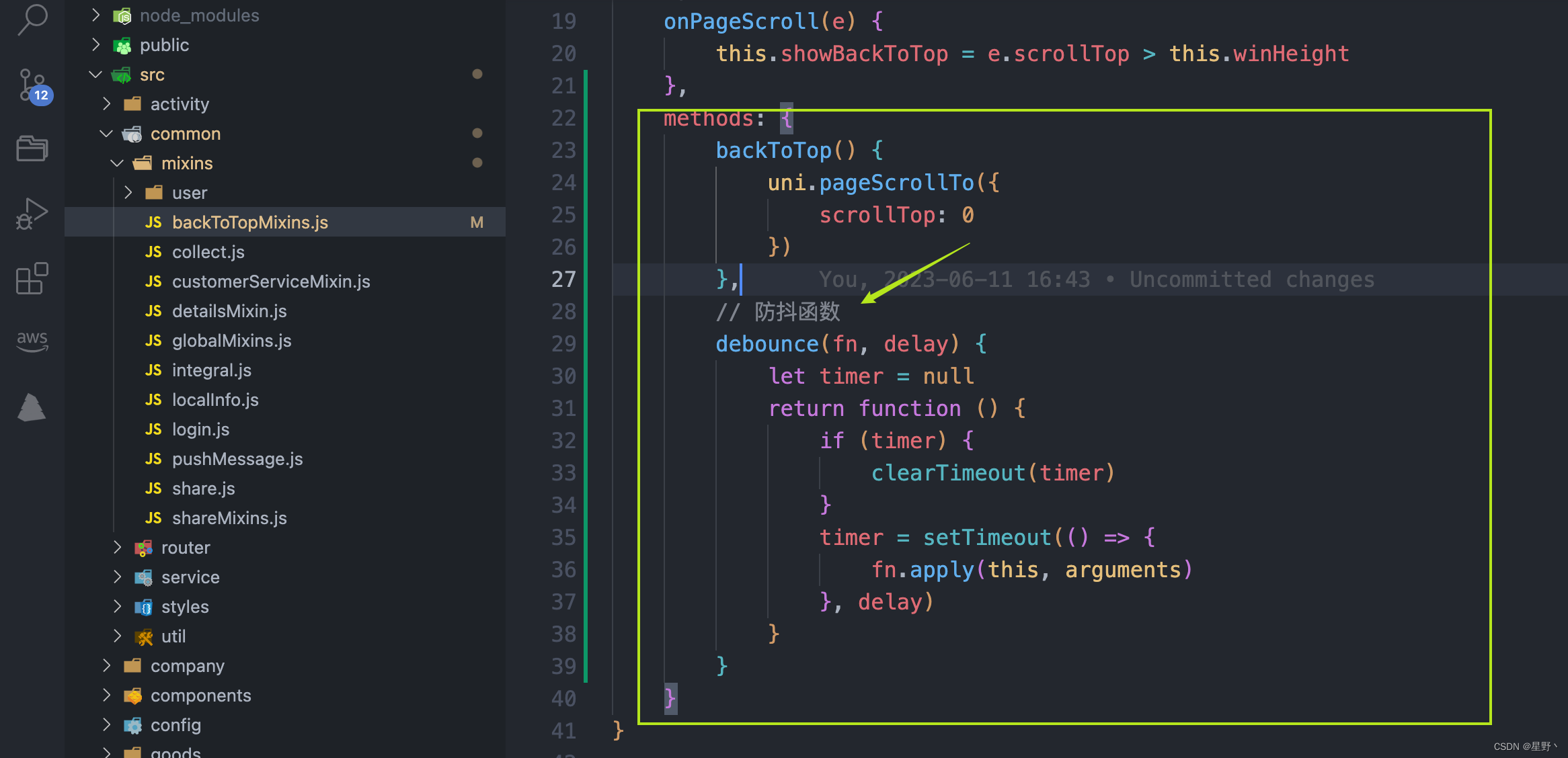
AWS CodeWhisperer 心得体会:安装与使用
大家好,今天我要和大家分享一下我在使用 AWS CodeWhisperer 这个工具时的心得体会。首先,让我们了解一下什么是 AWS CodeWhisperer。 什么是 AWS CodeWhisperer? AWS CodeWhisperer 是一个用于帮助开发者在 AWS 云平台上更轻松地编写、测试…...

高级查询 — 子查询
关于嵌套查询(子查询) 1.概述 子查询是在一个查询中嵌套另一个查询的查询语句。内部查询从外部查询或数据库中提取数据,然后使用这些数据来执行内部查询。出现在其他语句中的 select 语句,称为嵌套查询或子查询。外部的查询语句…...

霍夫变换(Hough Transform)
文章目录 1. 什么是霍夫变换2. 霍夫直线检测2.1 霍夫直线检测的具体步骤2.2 霍夫直线检测的优缺点2.3 OpenCV中霍夫直线检测的应用2.3.1 标准霍夫检测2.3.2 概率霍夫检测 3. 霍夫圆检测4. 源码仓库地址 1. 什么是霍夫变换 霍夫变换(Hough Transform)是图像处理中的一种特征提取…...

【每日挠头算法题(2)】压缩字符串|仅执行一次字符串交换能否使两个字符串相等
文章目录 一、压缩字符串思路 二、仅执行一次字符串交换能否使两个字符串相等思路1:计数法思路2:模拟法 总结 一、压缩字符串 点我直达~ 思路 使用双指针法 大致过程如下: 使用双指针,分别读(read)&…...

V4L2框架解析
和你一起终身学习,这里是程序员Android 经典好文推荐,通过阅读本文,您将收获以下知识点: 一、概览二、流程简介三、关键结构体四、模块初始化五、处理用户空间请求 一、概览 相机驱动层位于HAL Moudle与硬件层之间,借助linux内核驱…...
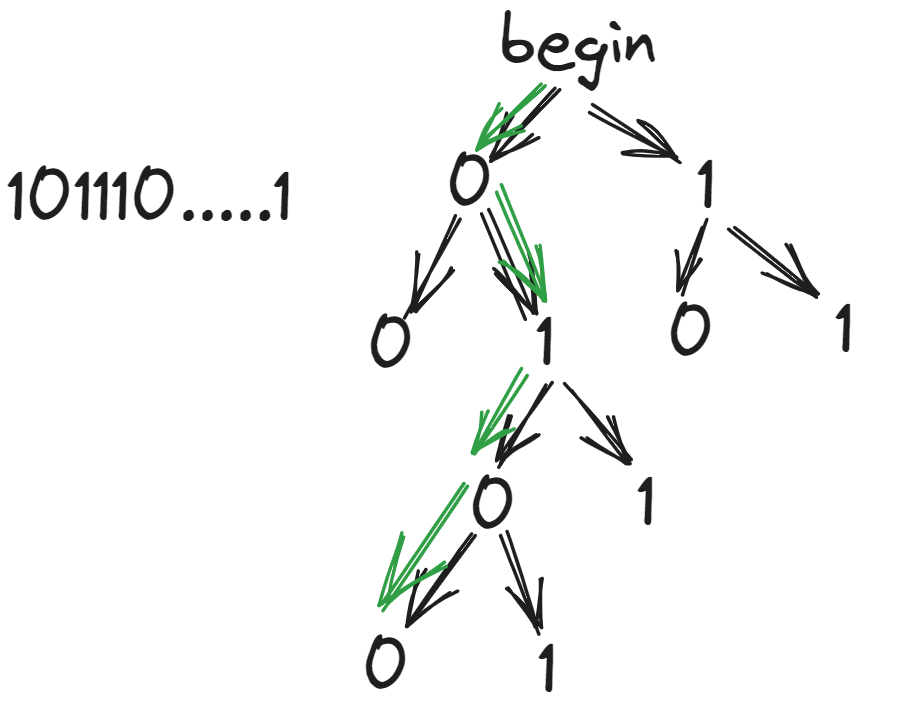
Trie树模板与应用
文章和代码已经归档至【Github仓库:https://github.com/timerring/algorithms-notes 】或者公众号【AIShareLab】回复 算法笔记 也可获取。 文章目录 Trie树(字典树)基本思想例题 Trie字符串统计code关于idx的理解 模板总结应用 最大异或对分…...
)
【华为OD统一考试B卷 | 200分】跳格子游戏(C++ Java JavaScript Python)
文章目录 题目描述输入描述输出描述用例C++javajavaScriptpython题目描述 地上共有N个格子,你需要跳完地上所有的格子,但是格子间是有强依赖关系的,跳完前一个格子后,后续的格子才会被开启,格子间的依赖关系由多组steps数组给出,steps[0]表示前一个格子,steps[1]表示st…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
