[ 靶场环境片 ] kali-linux采用Docker 搭建 pikachu（特别详细）
🍬 博主介绍
👨🎓 博主介绍：大家好，我是 _PowerShell ，很高兴认识大家~
✨主攻领域：【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】
🎉点赞➕评论➕收藏 == 养成习惯（一键三连）😋
🎉欢迎关注💗一起学习👍一起讨论⭐️一起进步📝文末有彩蛋
🙏作者水平有限，欢迎各位大佬指点，相互学习进步！
文章目录
- 🍬 博主介绍
- 一、pikachu介绍
- 1.Pikachu简介
- 2.Pikachu上的漏洞类型列表
- 二、windows搭建pikachu
- 三、Docker 搭建 pikachu
- 1.下载pikachu镜像
- 2.遇到拉取慢的情况下可以使用docker的国内镜像加速
- 3.启动pikachu容器
- <
相关文章：
[ 靶场环境片 ] kali-linux采用Docker 搭建 pikachu（特别详细）
🍬 博主介绍 👨🎓 博主介绍：大家好，我是 _PowerShell ，很高兴认识大家~ ✨主攻领域：【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 == 养成习惯（一键三连）😋 🎉欢迎关注💗一起学习👍一起讨论⭐️一起进步📝文末…...
阿里6面，成功唬住面试官拿了27K，软件测试面试也没有传说中那么难吧....
阿里的面试挺独特，每轮面试都没有 HR 约时间，一般是晚上 8 点左右面试官来一个电话，问是否能面试，能的话开始面，不能就约一个其它时间。 全程 6 面，前五面技术面，电话面试，最后一面…...
为什么静默安装未经过数字签名的驱动是不可行的?
我想，在 Windows XP 系统上，造成蓝屏的最主要原因是带有 Bug 的设备驱动程序。 请问在座的，谁赞成，谁反对。 因为驱动运行在内核模式，再也没有更高级别的组件对其进行行为监管，它可以做它想做的任何事情。…...
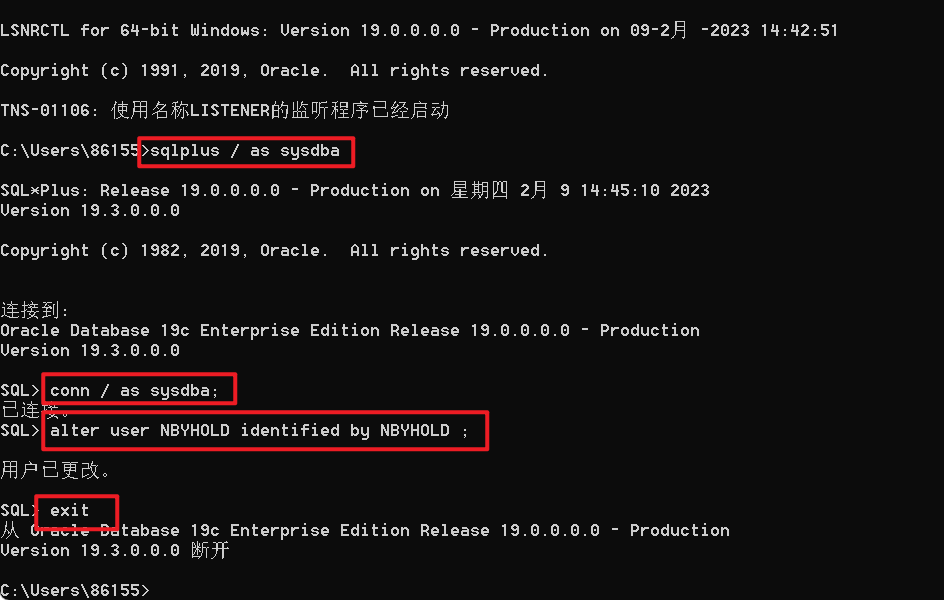
Caused by: java.sql.SQLException: ORA-28040: 没有匹配的验证协议
更改Oracle的配置文件：Oracle -> app -> ... ->...dbhome... -> admin重启Oracle:重启Oracle数据库的操作步骤1.查看监听器状态：lsnrctl status2.停止监听器：lsnrctl stop3.连接数据库：sqlplus / as sysdba4.停止数据…...
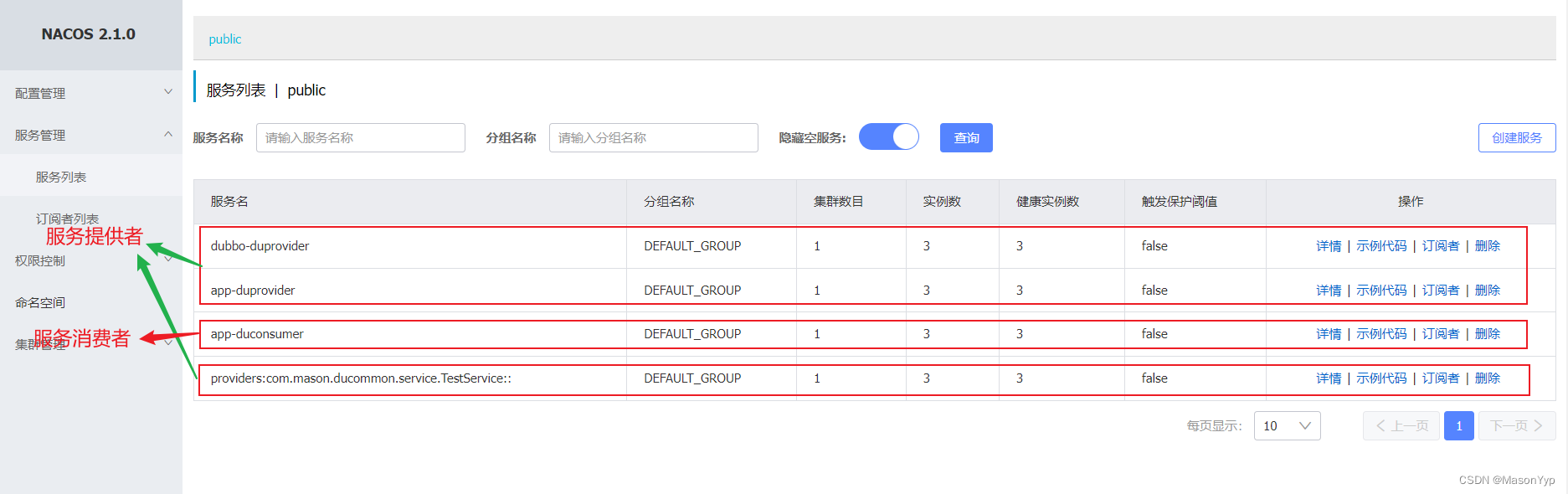
Dubbo3简单使用
Dubbo3简单使用 👉 使用Spring Boot实现Dubbo3，请参见以下地址。 # Dubbo3官网地址 https://cn.dubbo.apache.org/zh/# 使用SpringBoot实现Dubbo3的地址 https://cn.dubbo.apache.org/zh/docs3-v2/java-sdk/quick-start/spring-boot/# 该项目的git地址…...
Redis未授权漏洞蜜罐模拟与捕获分析
1.概述 文章主要分析Redis未授权漏洞的原理及形成原因，使用vulhub靶场进行漏洞复现，在了解漏洞原理并复现的基础上使用golang编写蜜罐代码进行模拟，开放端口在网上捕获真实存在的恶意攻击行为，对恶意样本进行分析，总结…...
Spring Security Oauth2.0认证授权
基本概念认证: 用户认证就是判断一个用户的身份是否合法的过程 ，用户去访问系统资源时系统要求验证用户的身份信息，身份合法方可继续访问，不合法则拒绝访问。常见的用户身份认证方式有:用户名密码登录，二维码登录，手机…...
安卓小游戏：贪吃蛇
安卓小游戏：贪吃蛇 前言 这个是通过自定义View实现小游戏的第二篇，实际上第一篇做起来麻烦点，后面的基本就是照葫芦画瓢了，只要设计下游戏逻辑就行了，技术上不难，想法比较重要。 需求 贪吃蛇࿰…...
CUDA中的图内存节点
CUDA中的图内存节点 文章目录CUDA中的图内存节点1. 简介2. 支持的架构和版本3. API基础知识3.1. 图节点 APIs3.2. 流捕获3.3. 在分配图之外访问和释放图内存3.4. cudaGraphInstantiateFlagAutoFreeOnLaunch4. 优化内存复用4.1. 解决图中的重用问题4.2. 物理内存管理和共享5. 性…...
你真的看好低代码开发吗？
低代码开发前景如何，大家真的看好低代码开发吗？之前有过很多关于低代码的内容，这篇就来梳理下国内外低代码开发平台发展现状及前景。 01、国外低代码开发平台现状 2014年，研究机构Forrester Research发表的报告中提到“面向客户…...
一篇带你MySQL运维
1. 日志 1.1 错误日志 错误日志是 MySQL 中 重要的日志之一，它记录了当 mysqld启动和停止时，以及服务器在运行过程中发生任何严重错误时的相关信息。当数据库出现任何故障导致无法正常使用时，建议首先查看此日志。 该日志是默认开启的&…...
《嵌入式 – GD32开发实战指南》第22章 SPI
开发环境： MDK：Keil 5.30 开发板：GD32F207I-EVAL MCU：GD32F207IK 22.1 SPI简介 SPI，是Serial Peripheral interface的缩写，顾名思义就是串行外围设备接口。是Motorola首先在其MC68HCXX系列处理器上定义的…...
一个优质软件测试工程师的简历应该有的样子（答应我一定要收藏起来）
个人简历 基本信息 姓 名：xxx 性 别： 女 年 龄：24 现住 地址： 深圳 测试 经验：3年 学 历：本科 联系 电话：18xxxxxxxx 邮 箱：xxxxl163.com 求职意向 应聘岗位：软件…...
C++ 浅谈之 STL Deque
C 浅谈之 STL Deque HELLO，各位博友好，我是阿呆 🙈🙈🙈 这里是 C 浅谈系列，收录在专栏 C 语言中 😜😜😜 本系列阿呆将记录一些 C 语言重要的语法特性 🏃&a…...
Koa2-项目中的基本应用
文章目录安装配置koa2配置nodemon,热更新我们的项目中间件什么是中间件👻洋葱模型路由中间件连接数据库 - mysql后端允许跨域处理请求getpostputdelete后续会继续更新安装配置koa2 👻安装 koa2 npm i koa2 -s👻在package.json 配置,当然是在…...
Flask入门（2）：配置
目录2.Flask配置2.1 直接写入主脚本2.2 系统环境变量2.3 单独的配置文件2.4 多个配置类2.5 Flask内置配置2.Flask配置 我们都知道，Flask应用程序肯定是需要各种各样的配置。来满足我们不同的需求的，这样可以使我们的应用程序更加灵活。比如可以根据需要…...
Linux--fork
一、fork入门知识 fork（）函数通过系统调用创建一个与原来进程几乎完全相同的进程，也就是两个进程可以做完全相同的事，但如果初始参数或者传入的变量不同，两个进程也可以做不同的事。可以简单地说fork()的作用就是创建一…...
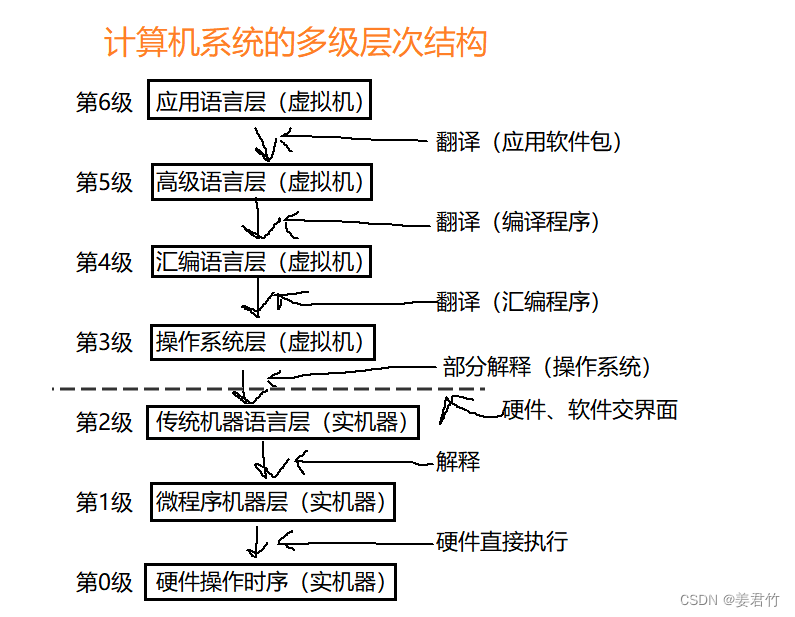
计算机组成原理（一）
1.了解计算机硬件的发展和软件的发展历程； 硬件： 电子管时代（1946-1959）：电子管、声汞延迟线、磁鼓 晶体管时代（1959-1964）：晶体管、磁芯 中、小规模集成电路时代&#…...
【SpringBoot】实现Async异步任务
1. 环境准备 在 Spring Boot 入口类上配置 EnableAsync 注解开启异步处理。 创建任务抽象类 AbstractTask，并分别配置三个任务方法 doTaskOne()，doTaskTwo()，doTaskThree()。 public abstract class AbstractTask {private static Random r…...
Node =＞Express学习
1.Express 能做什么 能快速构建web网站的服务器 或 Api接口的服务期 Web网站服务器，专门对外提供Web网页资源的服务器Api接口服务器：专门对外提供API接口的服务器 2.安装 在项目所处的目录中，运行以下命令，简装到项目中了 npm …...
以下是对华为 HarmonyOS NETX 5属性动画（ArkTS）文档的结构化整理，通过层级标题、表格和代码块提升可读性：
一、属性动画概述NETX 作用：实现组件通用属性的渐变过渡效果，提升用户体验。支持属性：width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项： 布局类属性（如宽高）变化时&#…...
Cesium1.95中高性能加载1500个点
一、基本方式： 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...
什么是库存周转？如何用进销存系统提高库存周转率？
你可能听说过这样一句话： “利润不是赚出来的，是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业，很多企业看着销售不错，账上却没钱、利润也不见了，一翻库存才发现： 一堆卖不动的旧货…...
Springcloud：Eureka 高可用集群搭建实战（服务注册与发现的底层原理与避坑指南）
引言：为什么 Eureka 依然是存量系统的核心？ 尽管 Nacos 等新注册中心崛起，但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制，是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...
tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录，但是由于这个树组件的节点越来越多，导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多，导致的浏览器卡顿，这里很明显就需要用到虚拟列表的技术&…...
springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生，小白用户，想学习知识的 有点基础，想要通过项…...
LLMs 系列实操科普（1）
写在前面： 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容，原视频时长 ~130 分钟，以实操演示主流的一些 LLMs 的使用，由于涉及到实操，实际上并不适合以文字整理，但还是决定尽量整理一份笔…...
stm32wle5 lpuart DMA数据不接收
配置波特率9600时，需要使用外部低速晶振...
华为OD最新机试真题-数组组成的最小数字-OD统一考试（B卷）
题目描述 给定一个整型数组，请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3，则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组，0<数组长度<= 100，0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
前端调试HTTP状态码
1xx（信息类状态码） 这类状态码表示临时响应，需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分，客户端应继续发送剩余部分。 2xx（成功类状态码） 表示请求已成功被服务器接收、理解并处…...