16 粒子滤波
文章目录
- 16 粒子滤波
- 16.1 背景介绍
- 16.1.1 Particle Filter是什么?
- 16.1.2 Patricle Filter的状态如何转移?
- 16.1.3 如何通过采样求解Particle Filter
- 16.2 重要性采样
- 16.2.1 重要性采样方法
- 16.2.2 Sequential Importance Sampling
- 16.2.3 Resampling
- 16.2.4 采样总结——Basic Particle Filter
- 16.3 具体算法——SIR Filter
16 粒子滤波
16.1 背景介绍
16.1.1 Particle Filter是什么?
Dynamic Model包含:
- HMM——关注Decoding问题
- Linear Dynamic System——关注Filtering问题
- Patricle Filter——Nan-Linear,Nan-Gauss,关注Filtering问题
16.1.2 Patricle Filter的状态如何转移?
在HMM中有 λ = ( π , A , B ) \lambda = (\pi, A, B) λ=(π,A,B),用于表示状态转移矩阵和发射矩阵。
由于Linear Dynamic System和Particle Filter中的隐变量与观测变量连续,状态转移矩阵和发射矩阵不用矩阵A、B表示,表示为:
Z t = g ( Z t − 1 , u , ε ) ↦ A X t = h ( Z t , u , δ ) ↦ B \begin{align} Z_t & = g(Z_{t-1}, u, \varepsilon) \mapsto A \\ X_t & = h(Z_t, u, \delta) \mapsto B \end{align} ZtXt=g(Zt−1,u,ε)↦A=h(Zt,u,δ)↦B
在Kalman Filter中我们假设以上两个公式均为线性,且噪声为Gauss。表示为:
Z t = A ⋅ Z t − 1 + B + ε ε ∽ N ( 0 , Q ) X t = C ⋅ Z t + D + δ δ ∽ N ( 0 , R ) \begin{align} Z_t & = A \cdot Z_{t-1} + B + \varepsilon & \varepsilon \backsim N(0, Q) \\ X_t & = C \cdot Z_t + D + \delta & \delta \backsim N(0, R) \end{align} ZtXt=A⋅Zt−1+B+ε=C⋅Zt+D+δε∽N(0,Q)δ∽N(0,R)
回顾:Kalman Filter通过预测+更新的方式求解Filtering问题
Step1: 求解Prediction问题
P ( Z t ∣ x 1 , … , x t − 1 ) = ∫ Z t − 1 P ( Z t ∣ Z t − 1 ) ⋅ P ( Z t − 1 ∣ x 1 , … , x t − 1 ) d Z t − 1 P(Z_{t} | x_1, \dots, x_{t-1}) = \int_{Z_{t-1}} P(Z_t | Z_{t-1}) \cdot P(Z_{t-1} | x_1, \dots, x_{t-1}) {\rm d}_{Z_{t-1}} P(Zt∣x1,…,xt−1)=∫Zt−1P(Zt∣Zt−1)⋅P(Zt−1∣x1,…,xt−1)dZt−1
Step2: 求解update问题
P ( Z t ∣ x 1 , … , x t ) ∝ P ( X t ∣ Z t ) ⋅ P ( Z t ∣ x 1 , … , x t − 1 ) P(Z_{t} | x_1, \dots, x_t) \propto P(X_t | Z_t) \cdot P(Z_t | x_1, \dots, x_{t-1}) P(Zt∣x1,…,xt)∝P(Xt∣Zt)⋅P(Zt∣x1,…,xt−1)
具体可以通过条件概率相互求解的公式求解。
而在Particle Filter中转移方程非线形非高斯,只能通过采样的方式求解。
16.1.3 如何通过采样求解Particle Filter
由于转移方程非线性非高斯,所以只能采取近似方法求解Filtering问题。这里使用Monte Carlo Method,通过采样求取期望:
P ( Z ∣ X ) → E Z ∣ X [ f ( z ) ] = ∫ Z f ( z ) ⋅ P ( Z ∣ X ) d Z ≈ 1 N ∑ i = 1 N f ( Z ( i ) ) P(Z|X) \rightarrow E_{Z|X}[f(z)] = \int_Z {f(z) \cdot P(Z|X)} {\rm d}Z \approx \frac{1}{N} \sum_{i=1}^N f(Z^{(i)}) P(Z∣X)→EZ∣X[f(z)]=∫Zf(z)⋅P(Z∣X)dZ≈N1i=1∑Nf(Z(i))
其中 Z ( i ) Z^{(i)} Z(i)为样本,且 Z ( 1 ) , Z ( 2 ) , … , Z ( N ) ∽ P ( Z ∣ X ) Z^{(1)}, Z^{(2)}, \dots, Z^{(N)} \backsim P(Z|X) Z(1),Z(2),…,Z(N)∽P(Z∣X)。
16.2 重要性采样
16.2.1 重要性采样方法
已知问题:
E [ f ( Z ) ] = ∫ f ( Z ) p ( Z ) d Z E[f(Z)] = \int f(Z) p(Z) {\rm d}Z E[f(Z)]=∫f(Z)p(Z)dZ
求解方法:
-
但 p ( Z ) p(Z) p(Z)的分布复杂,无法直接采样,所以我们引入已知分布 q ( Z ) q(Z) q(Z), q ( Z ) q(Z) q(Z)也称为提议分布(Proposed dist):
E [ f ( Z ) ] = ∫ f ( Z ) p ( Z ) d Z = ∫ f ( Z ) ⋅ p ( Z ) q ( Z ) ⋅ q ( Z ) d Z = 1 N ∑ i = 1 N f ( Z ( i ) ) ⋅ p ( Z ) q ( Z ) \begin{align} E[f(Z)] & = \int f(Z) p(Z) {\rm d}Z \\ & = \int f(Z) \cdot \frac{p(Z)}{q(Z)} \cdot q(Z) {\rm d}Z\\ & = \frac{1}{N} \sum_{i=1}^{N} f(Z^{(i)}) \cdot \frac{p(Z)}{q(Z)} \end{align} E[f(Z)]=∫f(Z)p(Z)dZ=∫f(Z)⋅q(Z)p(Z)⋅q(Z)dZ=N1i=1∑Nf(Z(i))⋅q(Z)p(Z) -
其中 p ( Z ) q ( Z ) \frac{p(Z)}{q(Z)} q(Z)p(Z)被称为weight,表示为 w ( i ) w^{(i)} w(i),用于表示提议分布与实际分布之间的相似度:
E [ f ( Z ) ] = 1 N ∑ i = 1 N f ( Z ( i ) ) ⋅ w ( i ) E[f(Z)] = \frac{1}{N} \sum_{i=1}^{N} f(Z^{(i)}) \cdot w^{(i)} E[f(Z)]=N1i=1∑Nf(Z(i))⋅w(i)
所以我们通过采样可以求出 f ( Z ( i ) ) f(Z^{(i)}) f(Z(i)),然后我们的目标就是求出对应的 w ( i ) w^{(i)} w(i)。
16.2.2 Sequential Importance Sampling
引入SIS的原因:
- 由于Filtering问题在递推过程中求解的是 P ( Z t ∣ X 1 : t ) P(Z_t | X_{1:t}) P(Zt∣X1:t),所以对应就会有 w t ( i ) = P ( Z t ∣ X 1 : t ) q ( Z t ( i ) ∣ X 1 : t ) w_t^{(i)} = \frac{P(Z_t | X_{1:t})}{q(Z_t^{(i)} | X_{1:t})} wt(i)=q(Zt(i)∣X1:t)P(Zt∣X1:t),但是随着 t t t增加,每次 w w w都要求 N N N遍,时间开销大。所以引入Sequential Importance Sampling,通过递推的方式求解 w w w( w t − 1 ( i ) → w t ( i ) w_{t-1}^{(i)} \rightarrow w_t^{(i)} wt−1(i)→wt(i))。
推导过程:
-
已知:
w t ( i ) ∝ P ( Z 1 : t ∣ X 1 : t ) q ( Z 1 : t ∣ X 1 : t ) w_t^{(i)} \propto \frac{P(Z_{1:t} | X_{1:t})}{q(Z_{1:t} | X_{1:t})} wt(i)∝q(Z1:t∣X1:t)P(Z1:t∣X1:t) -
分解 P ( Z 1 : t ∣ X 1 : t ) P(Z_{1:t} | X_{1:t}) P(Z1:t∣X1:t),其中将已知量(只由观测变量构成的数据)假设为常数:
P ( Z 1 : t ∣ X 1 : t ) = P ( Z 1 : t , X 1 : t ) P ( X 1 : t ) = 1 C ⋅ P ( X t ∣ Z 1 : t , X 1 : t − 1 ) ⋅ P ( Z t , X 1 : t − 1 ) = 1 C ⋅ P ( X t ∣ Z t ) ⋅ P ( Z t ∣ Z 1 : t − 1 , X 1 : t − 1 ) ⋅ P ( Z 1 : t − 1 , X 1 : t − 1 ) = 1 C ⋅ P ( X t ∣ Z t ) ⋅ P ( Z t ∣ Z t − 1 ) ⋅ P ( Z 1 : t − 1 , X 1 : t − 1 ) = 1 C ⋅ P ( X t ∣ Z t ) ⋅ P ( Z t ∣ Z t − 1 ) ⋅ P ( Z 1 : t − 1 ∣ X 1 : t − 1 ) ⋅ P ( X 1 : t − 1 ) = D C ⋅ P ( X t ∣ Z t ) ⋅ P ( Z t ∣ Z t − 1 ) ⋅ P ( Z 1 : t − 1 ∣ X 1 : t − 1 ) \begin{align} P(Z_{1:t} | X_{1:t}) & = \frac{P(Z_{1:t}, X_{1:t})}{P(X_{1:t})} \\ & = \frac{1}{C} \cdot P(X_t | Z_{1:t}, X_{1:t-1}) \cdot P(Z_t, X_{1:t-1}) \\ & = \frac{1}{C} \cdot P(X_t | Z_{t}) \cdot P(Z_t| Z_{1:t-1}, X_{1:t-1}) \cdot P(Z_{1:t-1}, X_{1:t-1}) \\ & = \frac{1}{C} \cdot P(X_t | Z_{t}) \cdot P(Z_t| Z_{t-1}) \cdot P(Z_{1:t-1}, X_{1:t-1}) \\ & = \frac{1}{C} \cdot P(X_t | Z_{t}) \cdot P(Z_t| Z_{t-1}) \cdot P(Z_{1:t-1}| X_{1:t-1}) \cdot P(X_{1:t-1}) \\ & = \frac{D}{C} \cdot P(X_t | Z_{t}) \cdot P(Z_t| Z_{t-1}) \cdot P(Z_{1:t-1}| X_{1:t-1}) \end{align} P(Z1:t∣X1:t)=P(X1:t)P(Z1:t,X1:t)=C1⋅P(Xt∣Z1:t,X1:t−1)⋅P(Zt,X1:t−1)=C1⋅P(Xt∣Zt)⋅P(Zt∣Z1:t−1,X1:t−1)⋅P(Z1:t−1,X1:t−1)=C1⋅P(Xt∣Zt)⋅P(Zt∣Zt−1)⋅P(Z1:t−1,X1:t−1)=C1⋅P(Xt∣Zt)⋅P(Zt∣Zt−1)⋅P(Z1:t−1∣X1:t−1)⋅P(X1:t−1)=CD⋅P(Xt∣Zt)⋅P(Zt∣Zt−1)⋅P(Z1:t−1∣X1:t−1)
通过以上推导可将 P ( Z 1 : t ∣ X 1 : t ) P(Z_{1:t} | X_{1:t}) P(Z1:t∣X1:t)分解为由 P ( Z 1 : t − 1 ∣ X 1 : t − 1 ) P(Z_{1:t-1}| X_{1:t-1}) P(Z1:t−1∣X1:t−1)组成的公式 -
分解 q ( Z 1 : t ∣ X 1 : t ) q(Z_{1:t} | X_{1:t}) q(Z1:t∣X1:t):
q ( Z 1 : t ∣ X 1 : t ) = q ( Z t ∣ Z 1 : t − 1 , X 1 : t ) ⋅ q ( Z 1 : t − 1 ∣ X 1 : t ) = q ( Z t ∣ Z 1 : t − 1 , X 1 : t ) ⋅ q ( Z 1 : t − 1 ∣ X 1 : t − 1 ) \begin{align} q(Z_{1:t} | X_{1:t}) & = q(Z_t | Z_{1:t-1}, X_{1:t}) \cdot q(Z_{1:t-1}| X_{1:t}) \\ & = q(Z_t | Z_{1:t-1}, X_{1:t}) \cdot q(Z_{1:t-1}| X_{1:t-1}) \end{align} q(Z1:t∣X1:t)=q(Zt∣Z1:t−1,X1:t)⋅q(Z1:t−1∣X1:t)=q(Zt∣Z1:t−1,X1:t)⋅q(Z1:t−1∣X1:t−1) -
结合起来就是:
w t ( i ) ∝ P ( Z 1 : t ∣ X 1 : t ) q ( Z 1 : t ∣ X 1 : t ) ∝ P ( X t ∣ Z t ) ⋅ P ( Z t ∣ Z t − 1 ) ⋅ P ( Z 1 : t − 1 ∣ X 1 : t − 1 ) q ( Z t ∣ Z 1 : t − 1 , X 1 : t ) ⋅ q ( Z 1 : t − 1 ∣ X 1 : t − 1 ) ∝ P ( X t ∣ Z t ) ⋅ P ( Z t ∣ Z t − 1 ) q ( Z t ∣ Z 1 : t − 1 , X 1 : t ) ⋅ w t − 1 ( i ) ∝ P ( X t ∣ Z t ) ⋅ P ( Z t ∣ Z t − 1 ) q ( Z t ∣ Z t − 1 , X 1 : t ) ⋅ w t − 1 ( i ) \begin{align} w_t^{(i)} & \propto \frac{P(Z_{1:t} | X_{1:t})}{q(Z_{1:t} | X_{1:t})} \\ & \propto \frac{P(X_t | Z_{t}) \cdot P(Z_t| Z_{t-1}) \cdot P(Z_{1:t-1}| X_{1:t-1})}{q(Z_t | Z_{1:t-1}, X_{1:t}) \cdot q(Z_{1:t-1}| X_{1:t-1})} \\ & \propto \frac{P(X_t | Z_{t}) \cdot P(Z_t| Z_{t-1})}{q(Z_t | Z_{1:t-1}, X_{1:t})} \cdot w_{t-1}^{(i)} \\ & \propto \frac{P(X_t | Z_{t}) \cdot P(Z_t| Z_{t-1})}{q(Z_t | Z_{t-1}, X_{1:t})} \cdot w_{t-1}^{(i)} \end{align} wt(i)∝q(Z1:t∣X1:t)P(Z1:t∣X1:t)∝q(Zt∣Z1:t−1,X1:t)⋅q(Z1:t−1∣X1:t−1)P(Xt∣Zt)⋅P(Zt∣Zt−1)⋅P(Z1:t−1∣X1:t−1)∝q(Zt∣Z1:t−1,X1:t)P(Xt∣Zt)⋅P(Zt∣Zt−1)⋅wt−1(i)∝q(Zt∣Zt−1,X1:t)P(Xt∣Zt)⋅P(Zt∣Zt−1)⋅wt−1(i)
具体可以表示为一个算法:
条件:t-1时刻的采样已完成 → w t − 1 ( i ) \rightarrow w_{t-1}^{(i)} →wt−1(i)已知。
t时刻:
for i = 1 to N:
Z t ( i ) ∽ q ( Z t ∣ Z t − 1 , X 1 : t ) Z_t^{(i)} \backsim q(Z_t | Z_{t-1}, X_{1:t}) Zt(i)∽q(Zt∣Zt−1,X1:t) // 采样
w t ( i ) ∝ P ( X t ∣ Z t ) ⋅ P ( Z t ∣ Z t − 1 ) q ( Z t ∣ Z t − 1 , X 1 : t ) ⋅ w t − 1 ( i ) w_t^{(i)} \propto \frac{P(X_t | Z_{t}) \cdot P(Z_t| Z_{t-1})}{q(Z_t | Z_{t-1}, X_{1:t})} \cdot w_{t-1}^{(i)} wt(i)∝q(Zt∣Zt−1,X1:t)P(Xt∣Zt)⋅P(Zt∣Zt−1)⋅wt−1(i) // 计算
endw t ( i ) w_t^{(i)} wt(i)要归一化, ∑ i = 1 N w t ( i ) \sum_{i=1}^{N} w_t^{(i)} ∑i=1Nwt(i)
但是通过SIS直接求解有一个问题: w t ( i ) w_t^{(i)} wt(i)的权值会退化——有的大有的小,随着维度上升,可能会出现如: w t ( 1 ) → 1 w_t^{(1)} \rightarrow 1 wt(1)→1但 w t ( N ) → 0 w_t^{(N)} \rightarrow 0 wt(N)→0的情况。解决方案有:
- Resampling——重采样(通过别的方法重新采样)
- 选择一个合适的proposed dist q(Z)
16.2.3 Resampling
这里介绍一种最简单的重采样方法。
倘若第一遍的采样结果为第二列:
| 数据编号 | 权重(weight) | cdf | |
|---|---|---|---|
| x ( 1 ) x^{(1)} x(1) | 0.1 | 0.1 | 0.1 |
| x ( 2 ) x^{(2)} x(2) | 0.1 | 0.1 | 0.2 |
| x ( 3 ) x^{(3)} x(3) | 0.8 | 0.8 | 1 |
我们将权重假设为当前数据的概率,通过权重建立概率密度函数,并求出其分布函数,即可通过分段函数进行采样。
这样的优点是可以将数据集中在权重大的地方。
16.2.4 采样总结——Basic Particle Filter
结合:重要性采样方法+SIS+Resampling,就是简单的粒子滤波求解方案:Basic Particle Filter
16.3 具体算法——SIR Filter
Particle Filter整体就是通过每个时刻的采样与迭代地计算权重,通过Monte Carlo方法预测的方法。
根据16.2.2已知迭代公式为:
w t ( i ) ∝ P ( X t ∣ Z t ) ⋅ P ( Z t ∣ Z t − 1 ) q ( Z t ∣ Z t − 1 , X 1 : t ) ⋅ w t − 1 ( i ) w_t^{(i)} \propto \frac{P(X_t | Z_{t}) \cdot P(Z_t| Z_{t-1})}{q(Z_t | Z_{t-1}, X_{1:t})} \cdot w_{t-1}^{(i)} wt(i)∝q(Zt∣Zt−1,X1:t)P(Xt∣Zt)⋅P(Zt∣Zt−1)⋅wt−1(i)
其中我们令 q ( Z t ∣ Z t − 1 , X 1 : t ) q(Z_t | Z_{t-1}, X_{1:t}) q(Zt∣Zt−1,X1:t)为用于采样的分布,我们假设采样的分布就是状态转移函数:
q ( Z t ∣ Z t − 1 , X 1 : t ) = p ( Z t ∣ Z t − 1 ( i ) ) q(Z_t | Z_{t-1}, X_{1:t}) = p(Z_t | Z_{t-1}^{(i)}) q(Zt∣Zt−1,X1:t)=p(Zt∣Zt−1(i))
可以简化计算,算法可以总结为"generate and test":
-
generate表示采样:采样的方式变成了:
Z t ( i ) ∽ q ( Z t ∣ Z t − 1 , X 1 : t ) ⟹ Z t ( i ) ∽ p ( Z t ∣ Z t − 1 ( i ) ) Z_t^{(i)} \backsim q(Z_t | Z_{t-1}, X_{1:t}) \implies Z_t^{(i)} \backsim p(Z_t | Z_{t-1}^{(i)}) Zt(i)∽q(Zt∣Zt−1,X1:t)⟹Zt(i)∽p(Zt∣Zt−1(i)) -
test表示通过权重的迭代计算进行预测:变成了:
w t ( i ) ∝ P ( X t ∣ Z t ( i ) ) ⋅ w t − 1 ( i ) w_t^{(i)} \propto P(X_t | Z_{t}^{(i)}) \cdot w_{t-1}^{(i)} wt(i)∝P(Xt∣Zt(i))⋅wt−1(i)
上面的方法总结下来就是:SIR Filter(Sampling-Importance-Resampling)——SIS + Resampling + ( q ( Z t ∣ Z t − 1 , X 1 : t ) = p ( Z t ∣ Z t − 1 ( i ) ) q(Z_t | Z_{t-1}, X_{1:t}) = p(Z_t | Z_{t-1}^{(i)}) q(Zt∣Zt−1,X1:t)=p(Zt∣Zt−1(i)))
相关文章:

16 粒子滤波
文章目录 16 粒子滤波16.1 背景介绍16.1.1 Particle Filter是什么?16.1.2 Patricle Filter的状态如何转移?16.1.3 如何通过采样求解Particle Filter 16.2 重要性采样16.2.1 重要性采样方法16.2.2 Sequential Importance Sampling16.2.3 Resampling16.2.4…...

【appium】appium自动化入门之API(下)——两万字API长文,建议收藏
目录 Appium API 前言 1.contexts (返回当前会话中的上下文,使用后可以识别 H5 页面的控件) 2.current_context (返回当前会话的当前上下文 ) 3. context (返回当前会话的当前上下文) 4.find_e…...

开发改了接口,经常忘通知测试的解决方案!
目录 前言: Apifox解决方案 Apifox对此给出的解决方案是: 用Apifox怎么处理接口变更 接口代码实现逻辑修改 接口参数修改 前言: 在开发过程中,接口变动十分频繁,测试人员没有及时获得相关通知的情况也很普遍。这…...
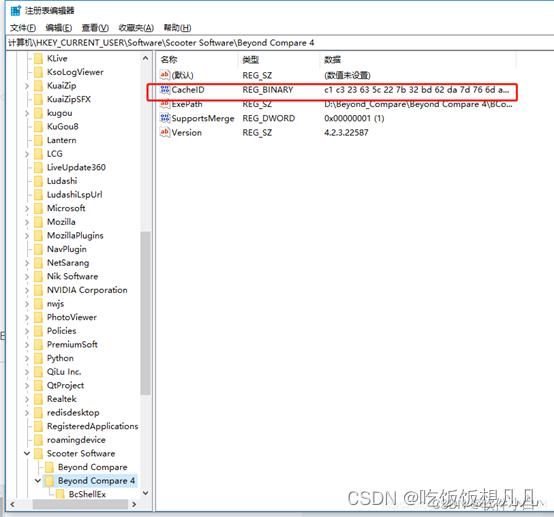
Beyond Compare 4 无法打开
解决办法: 1.修改注册表。WINR呼出开始菜单,在搜索栏中输入 regedit,点击确定。 2.删除项目:\HKEY_CURRENT_USER\Software\ScooterSoftware\Beyond Compare 4\CacheId 根据这个路径找到cacheid 右击删除掉就可以...

MySQL高级数据操作
✅作者简介:热爱Java后端开发的一名学习者,大家可以跟我一起讨论各种问题喔。 🍎个人主页:Hhzzy99 🍊个人信条:坚持就是胜利! 💞当前专栏:MySQL 🥭本文内容&a…...
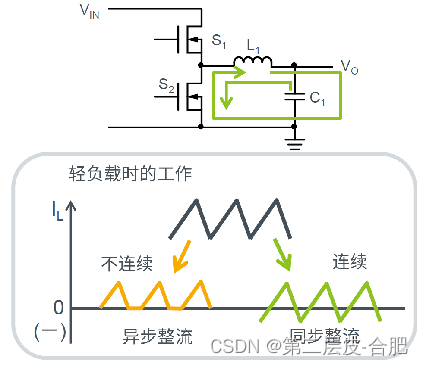
硬件设计电源系列文章-DCDC转换器基础知识
文章目录 概要整体架构流程技术名词解释技术细节小结 概要 提示:这里可以添加技术概要 本文主要接着上篇,上篇文章主要讲述了LDO的相关基础知识,本节开始分享DCDC基础知识 整体架构流程 提示:这里可以添加技术整体架构 以下是…...
XdsObjects .NET 8.45.1001.0 Crack
XdsObjects 是一个工具包,允许开发人员使用 IHE XDS 和 XDS-I 配置文件开发应用程序,只需花费最少的时间和精力,因为遵守配置文件和 ebXML 规则的所有艰苦工作都由该工具包处理。 它为所有角色提供客户端和服务器支持,包括&#…...
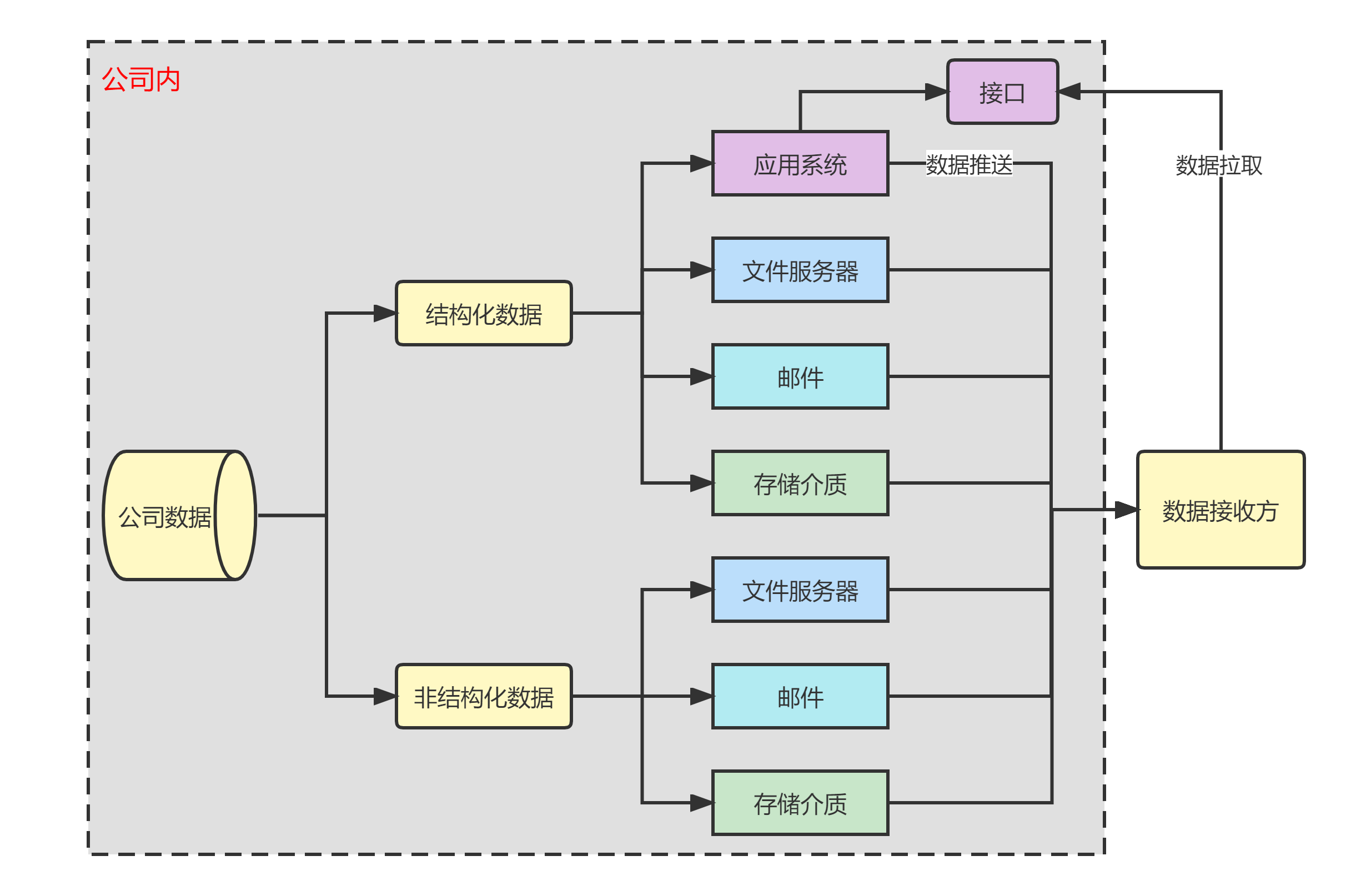
数据安全--17--数据安全管理之数据传输
本博客地址:https://security.blog.csdn.net/article/details/131061729 一、数据传输概述 数据传输有两个主体,一个是数据发送方,另一个是数据接收方。数据在通过不可信或者较低安全性的网络进行传输时,容易发生数据被窃取、伪…...

SpringSecurity实现前后端分离登录token认证详解
目录 1. SpringSecurity概述 1.1 权限框架 1.1.1 Apache Shiro 1.1.2 SpringSecurity 1.1.3 权限框架的选择 1.2 授权和认证 1.3 SpringSecurity的功能 2.SpringSecurity 实战 2.1 引入SpringSecurity 2.2 认证 2.2.1 登录校验流程 2.2.2 SpringSecurity完整流程 2.2.…...

Vue3_ElementPlus_简单增删改查(2023)
Vue3,Element Plus简单增删改查 代码:https://github.com/xiaoming12318/Vue3_ElementPlus_CRUD.git 环境: Visual Studio Code Node.js 16.0或更高版本,https://nodejs.org/en axios 快速上手: 如果已经有16.0及…...
vue中重写并自定义console.log
0. 背景 在vue2项目中自定义console.log并输出文件名及行、列号 1. 实现 1.1 自定义console.log export default {// 输出等级: 0-no, 1-error, 2-warning, 3-info, 4-debug, 5-loglevel: 5,// 输出模式: 0-default, 1-normal, 2-randommode: 1,// 是否输出图标hasIcon: fal…...
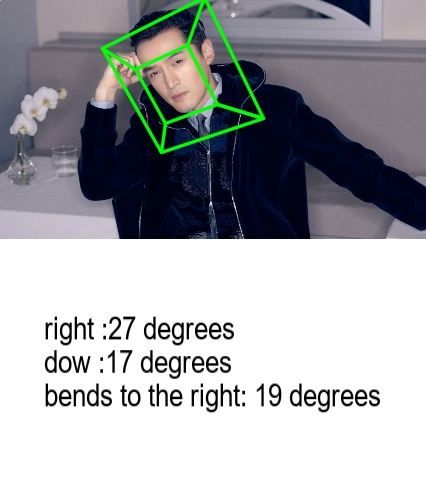
基于OpenCV 和 Dlib 进行头部姿态估计
写在前面 工作中遇到,简单整理博文内容涉及基于 OpenCV 和 Dlib头部姿态评估的简单Demo理解不足小伙伴帮忙指正 庐山烟雨浙江潮,未到千般恨不消。到得还来别无事,庐山烟雨浙江潮。 ----《庐山烟雨浙江潮》苏轼 https://github.com/LIRUILONGS…...
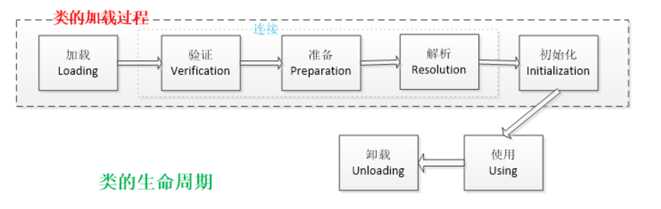
24个Jvm面试题总结及答案
1.什么是Java虚拟机?为什么Java被称作是“平台无关的编程语言”? Java虚拟机是一个可以执行Java字节码的虚拟机进程。Java源文件被编译成能被Java虚拟机执行的字节码文件。 Java被设计成允许应用程序可以运行在任意的平台,而不需要程序员为每…...

freemarker 生成前端文件
Freemarker是一种模板引擎,它允许我们在Java应用程序中分离视图和业务逻辑。在Freemarker中,List是一种非常有用的数据结构,它允许我们存储一组有序的元素。有时候,我们需要判断一个List是否为空,这在程序设计中有许多…...

Pycharm+pytest+allure打造高逼格的测试报告
目录 前言: 1、安装allure 2、安装allure-pytest 3、一个简单的用例test_simpe.py 4、在pycharm底部打开terminal 5、用allure美化报告 6、查看报告 总结: 前言: 今天分享的内容:在Pycharmpytest基础上使用allure打造高逼格…...
Mybatis-Plus中update更新操作用法
目录 一、前言二、update1、关于修改的4个条件构造器2、UpdateWrapper【用法示例】3、LambdaUpdateWrapper【用法示例】4、UpdateChainWrapper【 用法示例】5、LambdaUpdateChainWrapper【 用法示例】6、updateById 和 updateBatchById7、Mybatis-plus设置某个字段值为null的方…...

16道JVM面试题
1.jvm内存布局 1.程序计数器:当前线程正在执行的字节码的行号指示器,线程私有,唯一一个没有规定任何内存溢出错误的情况的区域。 2.Java虚拟机栈:线程私有,描述Java方法执行的内存模型,每个方法运行时都会…...
HttpRunner 接口自动化测试框架实战,打造高效测试流程
简介 2018年python开发者大会上,了解到HttpRuuner开源自动化测试框架,采用YAML/JSON格式管理用例,能录制和转换生成用例功能,充分做到用例与测试代码分离,相比excel维护测试场景数据更加简洁。在此,利用业…...
手写一个webpack插件(plugin)
熟悉 vue 和 react 的小伙伴们都知道,在执行过程中会有各种生命周期钩子,其实webpack也不例外,在使用webpack的时候,我们有时候需要在 webpack 构建流程中引入自定义的行为,这个时候就可以在 hooks 钩子中添加自己的方…...

jvm常见面试题
0x01. 内存模型以及分区,需要详细到每个区放什么。 栈区: 栈分为java虚拟机栈和本地方法栈 重点是Java虚拟机栈,它是线程私有的,生命周期与线程相同。 每个方法执行都会创建一个栈帧,用于存放局部变量表࿰…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
