【数学建模系列】TOPSIS法的算法步骤及实战应用——MATLAB实现
文章目录
- TOPSIS简介
- 方法和原理
- 数学定义
- 数学语言描述
- 现实案例
- 正负理想解
- 定义
- 实例
- 量纲
- TOPSIS法的算法步骤
- 1.用向量规范化的方法求得规范决策矩阵
- 2.构成加权规范阵C=(c~ij~)~m*n~
- 3.确定正负理想解的距离
- 4.计算各方案到正理想解与负理想解的距离
- 5.计算各方案的综合评价指数
- 6.排列方案的优劣次序
- 实战应用
- 例题
- 解答步骤
- **数据的预处理**
- **属性值线性规划归一化**
- MATLAB代码(建议对照上方 “TOPSIS法的算法步骤” 查看)
- 完整代码
TOPSIS简介
客观评价方法中的一种,亦称为理想解法,是一种有效的多指标评价方法。这种方法通过构造评价问题的正理想解和负理想解,即各指标的最优解和最劣解,通过计算每个方案到理想方案的相对贴近度,即靠近止理想解和远离负理想解的程度,来对方案进行排序,从而选出最优方案。
方法和原理
数学定义
数学语言描述
设多属性决策方案集为D={d1,d2,…,dm},衡量方案优劣的属性变量为x1,…,xn,,这时方案集D中的每个方案di( i= 1,…,m )的n个属性值构成的向量是[Ai1,…,Ain],它作为n维空间中的一个点,能唯一地表征方案di。
现实案例
例如评价经济的发展水平
d1代表山东,d2代表江苏,d3代表北京……就是一共有m个待评价方案。
x1是绿化面积,x2是人均GDP,x3是经济总量……共有n个属性值。
其中能够展现山东的经济发展水平有绿化面积、人均GDP、经济总量等n个指标。而Ai1就是山东绿化的总面积、Ai2为山东GDP总量……
正负理想解
定义
正理想解C是一个方案集D中并不存在的虚拟的最佳方案,它的每个属性值都是决策矩阵中该属性的最好值;而负理想解C0则是虚拟的最差方案,它的每个属性值都是决策矩阵中该属性的最差值。在n维空间中,将方案集D中的各备选方案di与正理想解C和负理想解C0的距离进行比较,既靠近正理想解又远离负理想解的方案就是方案集D中的最佳方案;并可以据此排定方案集D中各备选方案的优先序。
实例

评价表中哪五个研究生院更好,可以虚构一个最好的研究生院标准,该虚构的研究生院的数据全为最优值,例如:
虚构研究生院6,其中它的人均专著x61为1.2,生师比x62为5(生师比为学生和老师的比值,它的值必须保持适度,适当的生师比可以促进老师和学生良好的互动,该值过高过低都不好),科研经费x63为10000,预期毕业率x64为1.8。此时,研究生院6就是正理想解C*,同理构建虚拟的最差方案负理想解C0。
| – | x1 | x2 | x3 | x4 |
|---|---|---|---|---|
| C*(正理想解) | 1.2 | 5 | 10000 | 1.8 |
| C0(负理想解) | 0.1 | 10 | 400 | 6.7 |
量纲
确定好正负理想解后,就可以以此来判断判断不同研究生院的优劣。下面开始描述每个研究生院与正负理想解的距离。
那么距离应该怎么算呢?当量纲不同时,方案不同数据的波动会很大,因此在计算距离时首先要排除量纲的影响,进行非量纲化。
非量纲化定义
多属性决策与评估的困难之一是属性间的不可公度性,即在属性值表中的每一列数具有不同的单位(量纲)。即使对同一属性,采用不同的计量单位,表中的数值也就不同。在用各种多属性决策方法进行分析评价时,需要排除量纲的选用对决策或评估结果的影响,这就是非量纲化。
TOPSIS法的算法步骤
1.用向量规范化的方法求得规范决策矩阵
设多属性决策问题的决策矩阵A=(aij )m*n,规范化决策矩阵B=(bij)m*n,其中

2.构成加权规范阵C=(cij)m*n
设由决策人给定各属性的权重向量为 w=[w1,w2,…,wn] ,
则 cij = wj*bij
其中 i=1,2,…,m, j =1,2,…,n.
在评价过程中,每项评价标准占比不同,让重要的指标影响大一点,不重要的指标影响小一点。
类似于成绩的计算,比较重要的语数英总分数高一些,其他副科的总分数低一些。
3.确定正负理想解的距离
理想解属性大致可以分为效益型、成本型和区间型三种,其中
正理想解:

效益最大值和成本最小值,当属性为区间型的时候要判断在哪个区间最佳。
负理想解:

效益最小值和成本最大值
4.计算各方案到正理想解与负理想解的距离
备选方案di到正理想解的距离为:

备选方案di到负理想解的距离为:

可类比两点间距离公式,该距离为n维空间内的距离
5.计算各方案的综合评价指数

计算综合评价指数公式的分子为方案到负理想解的距离,分母为为方案到负理想解的距离与方案到正理想解的距离之和,所以综合评价指数越大越好。
6.排列方案的优劣次序
按综合评价指数由大到小排列方案的优劣次序即可
实战应用
例题
研究生院试评估
为了客观地评价我国研究生教育的实际状况和各研究生院的教学质量,国务院学位委员会办公室组织过一次研究生院的评估。为了取得经验,先选5所研究生院,收集有关数据资料进行了试评估,表1是所给出的部分数据。

解答步骤
数据的预处理
数据的预处理又称属性值的规范化
属性值具有多种类型,包括效益型、成本型和区间型等。这三种属性,效益型属性越大越好,成本型属性越小越好,区间型属性是在某个区间最佳。
判断每个属性的数据是越大越好还是越小越好,当属性为区间型的时候判断在哪个区间最佳。
判断完成以后将它们进行规范化处理。
数据规范化处理的作用
1.属性值有多种类型,上述三种属性放在同一个表中不便于直接从数值大小判断方案的优劣,因此需要对数据进行预处理,使得表中任一属性下性能越优的方案变换后的属性值越大。
2.非量纲化,多属性决策与评估的困难之一是属性间的不可公度性,即在属性值表中的每一列数具有不同的单位(量纲)。即使对同一属性,采用不同的计量单位,表中的数值也就不同。在用各种多属性决策方法进行分析评价时,需要排除量纲的选用对决策或评估结果的影响,这就是非量纲化。
3.归一化,属性值表中不同指标的属性值的数值人小差别很大,为了直观,更为了便于采用各种多属性决策与评估方法进行评价,需要把属性值表中的数值归一化,即把表中数值均变换到[0,1]区间上。
即将上述三种属性全部转化为效益型,这个数值分布在[0,1]区间上,该值越大越好。
属性值线性规划归一化
为了使每个属性变换后的最优值为1且最差值为0,可以进行标准0-1变换。
**1.对效益型属性xj,令
当aij为最小值时,bij为0,当aij为最大值时,bij为1。**
2.对成本型属性xj,
计算公式可套用效益型的公式,在求正负理想解的时候记得要颠倒一下。
**3.对区间型属性xj,设给定的最优属性区间为[ a j 0 a^0_j aj0, a j ∗ a^*_j aj∗], a j , a^,_j aj,为无
法容忍下限, a j ” a^”_j aj”为无法容忍上限,则
例如例题中的生师比,它最好的区间应为[5,6],最差应不低于2,高于12,当该属性值在最有区间时为1,当超过或等于能容忍上下限时为0。**
MATLAB代码(建议对照上方 “TOPSIS法的算法步骤” 查看)
注:以下并非C语言
clc,clear
% clc:清除命令窗口的内容,对工作环境中的全部变量无任何影响
% clear:清除工作空间的所有变量a=[0.1 5 5000 4.70.2 6 6000 5.60.4 7 7000 6.70.9 10 10000 2.31.2 2 400 1.8];
% 输入数据[m,n]=size(a);
%这行代码的作用是获取矩阵a的维度信息,其中m表示a的行数,n表示a的列数。其中,size函数返回的是一个含有两个元素的向量,第一个元素表示矩阵的行数,第二个元素表示矩阵的列数。因此,在这个代码中,m和n就被赋值为了矩阵a的行数和列数。在后续的代码中,可以使用这两个变量来控制循环等操作。% @是用于定义函数句柄的操作符。函数句柄既是一种变量,可以用于传参和赋值;也是可以当做函数名一样使用,该步骤类似于C语言中的构造函数。
x2=@(qujian,lb,ub,x)(1-(qujian(1)-x)./(qujian(1)-lb)).*(x>=lb&x<qujian(1))+...(x>=qujian(1)&x<=qujian(2))+(1-(x-qujian(2))./(ub-qujian(2))).*...(x>qujian(2)&x<=ub);
qujian=[5,6];lb=2;ub=12;
a(:,2)=x2(qujian,lb,ub,a(:,2));
%该函数可以实现将区间型属性转换为效益型属性的,实现下图所示公式

注:如果 (x>=qujian(1)&x<=qujian(2)) 成立,结果为真,值为1;如果 x 的值没有出现在上述区间,结果为假,值为0。
加权处理
for j=1:nb(:,j)=a(:,j)/norm(a(:,j));%向量规范化
end
实现该式:

%设权向量为w=[0.2,0.3,0.4,0.1]
w=[0.2 0.3 0.4 0.1];
c=b.*repmat(w,m,1);%求出加权规范阵
至此步骤2完成,得出加权的向量规范化属性矩阵

正负理想解
cstar=max(c);%求正理想解
cstar(4)=min(c(:,4))%属性4为成本型,与效益型相反
c0=min(c);%求负理想解
c0(4)=max(c(:,4))%属性4为成本型,与效益型相反for i=1:msstar(i)=norm(c(i,:)-cstar);%求到正理想解的距离s0(i)=norm(c(i,:)-c0);%求到负理想解的距离
end
按顺序依次实现
求到正理想解的距离:

求到负理想解的距离:

f=s0./(sstar+s0);
[sf,ind]=sort(f,'descend') %求排序结果
% "ascend"时,进行升序排序,为"descend "时,进行降序排序
计算各方案的综合评价指数:

得出结果
各方案的从优到劣的次序为4,3,2,1,5
完整代码
clc,clear
% clc:清除命令窗口的内容,对工作环境中的全部变量无任何影响
% clear:清除工作空间的所有变量a=[0.1 5 5000 4.70.2 6 6000 5.60.4 7 7000 6.70.9 10 10000 2.31.2 2 400 1.8];
% 输入数据
[m,n]=size(a);
x2=@(qujian,lb,ub,x)(1-(qujian(1)-x)./(qujian(1)-lb)).*(x>=lb&x<qujian(1))+...(x>=qujian(1)&x<=qujian(2))+(1-(x-qujian(2))./(ub-qujian(2))).*...(x>qujian(2)&x<=ub);
qujian=[5,6];lb=2;ub=12;
a(:,2)=x2(qujian,lb,ub,a(:,2));%对属性2进行变换for j=1:nb(:,j)=a(:,j)/norm(a(:,j));%向量规范化
end
w=[0.2 0.3 0.4 0.1];
c=b.*repmat(w,m,1);%求加权矩阵cstar=max(c);%求正理想解
cstar(4)=min(c(:,4))%属性4为成本型
c0=min(c);%求负理想解
c0(4)=max(c(:,4))%属性4为成本型的for i=1:msstar(i)=norm(c(i,:)-cstar);%求到正理想解的距离s0(i)=norm(c(i,:)-c0);%求到负理想解的距离
end
f=s0./(sstar+s0);
[sf,ind]=sort(f,'descend') %求排序结果
% "ascend"时,进行升序排序,为"descend "时,进行降序排序
负理想解
c0(4)=max(c(:,4))%属性4为成本型的for i=1:msstar(i)=norm(c(i,:)-cstar);%求到正理想解的距离s0(i)=norm(c(i,:)-c0);%求到负理想解的距离
end
f=s0./(sstar+s0);
[sf,ind]=sort(f,'descend') %求排序结果
% "ascend"时,进行升序排序,为"descend "时,进行降序排序
相关文章:

【数学建模系列】TOPSIS法的算法步骤及实战应用——MATLAB实现
文章目录 TOPSIS简介方法和原理数学定义数学语言描述现实案例 正负理想解定义实例 量纲 TOPSIS法的算法步骤1.用向量规范化的方法求得规范决策矩阵2.构成加权规范阵C(c~ij~)~m*n~3.确定正负理想解的距离4.计算各方案到正理想解与负理想解的距离5.计算各方案的综合评价指数6.排列…...
工具)
网络安全(黑客)工具
1.Nmap 它是网络管理员 必用的软件之一,以及用以评估网络系统安全。正如大多数被用于网络安全的工具,nmap 也是不少黑客及骇客(又称脚本小子 )爱用的工具 。系统管理员可以利用nmap来探测工作环境中未经批准使用的服务器ÿ…...

探究前后端数据交互方式
前端和后端在 Web 开发中扮演着不同的角色,两者需要进行数据的传递和交互。本篇文章将主要讨论前后端数据交互方式的不同类型和应用场景。 一、什么是前后端数据交互? 在 Web 开发中,前端负责用户界面的设计和交互,后端负责数据…...

Yolov5轻量化:CVPR2023|RIFormer:无需TokenMixer也能达成SOTA性能的极简ViT架构
1.RIFormer介绍 论文:https://arxiv.org/pdf/2304.05659.pdf 本文基于重参数机制提出了RepIdentityFormer方案以研究无Token Mixer的架构体系。紧接着,作者改进了学习架构以打破无Token Mixer架构的局限性并总结了优化策略。搭配上所提优化策略后,本文构建了一种极致简单且…...
Spring-Retry实现及原理
前言 重试,其实我们其实很多时候都需要的,为了保证容错性,可用性,一致性等。一般用来应对外部系统的一些不可预料的返回、异常等,特别是网络延迟,中断等情况。还有在现在流行的微服务治理框架中࿰…...

Java中的锁
为什么会有这些锁呢? 因为一种类型的锁很难应对线程操作同步资源的情况。 乐观锁和悲观锁 自旋锁和适应性自旋锁 无锁、偏向锁、轻量级锁和重量级锁 公平锁和非公平锁 可重入锁和非可重入锁 乐观锁和悲观锁 悲观锁认为当它操作数据的时候,必然用一…...

学习系列:5种常见的单例模式变体及其实现方式
单例模式是一种创建型设计模式,它保证一个类只有一个实例,并提供了一个全局访问点。在实际应用中,我们可能会遇到一些特殊情况,需要对单例模式进行一些变体,以满足不同的需求。下面介绍几种常见的单例模式变体。 1. 懒…...
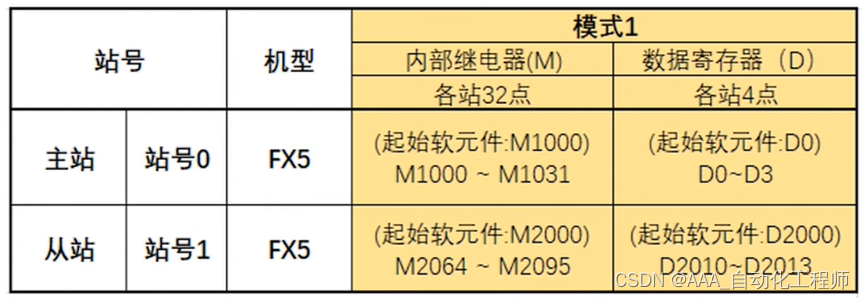
三菱FX5U系列PLC之间进行简易PLC间链接功能的具体方法
三菱FX5U系列PLC之间进行简易PLC间链接功能的具体方法 功能介绍: 在最多8台FX5U或者FX3U PLC之间通过RS-485通信方式连接,进行软元件相互链接的功能。 接线注意事项: 根据链接模式和所使用的从站数量的不同,链接软元件的占用点数也有所变化。根据链接软元件的起始编号,对占…...
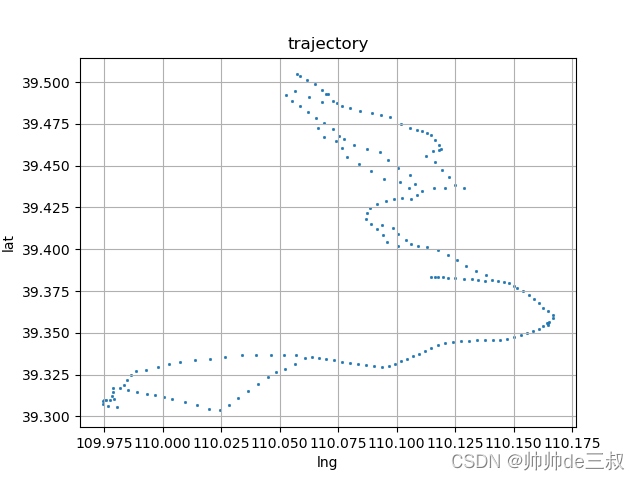
基于DBACAN的道路轨迹点聚类
目录 前言道路栅格化轨迹聚类参考资料 前言 很多针对道路轨迹的挖掘项目前期都需要对道路进行一段一段的分割成路段,然后对每一个路段来单独进行考察,如设定路段限速标识,超速概率等,如何对道路进行划分,其实是一个很…...
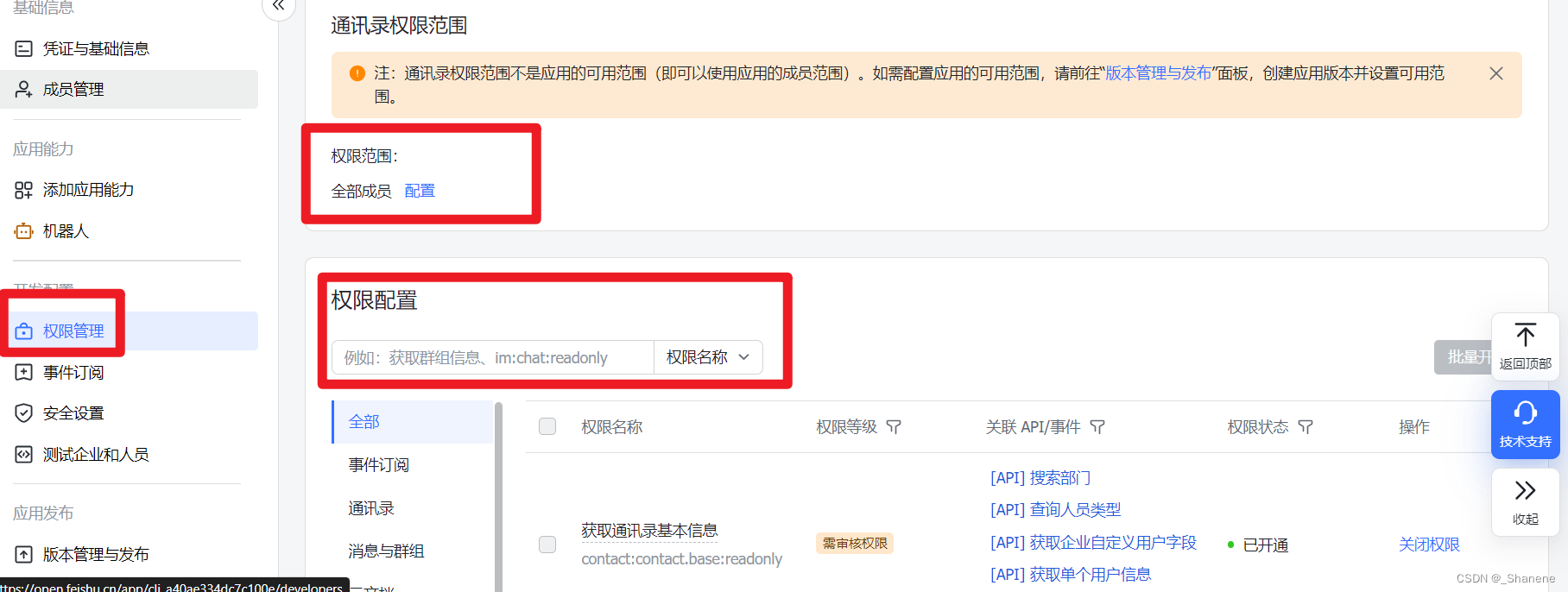
【项目】接入飞书平台
前言 项目有和飞书打通的需求,因为是第一次打通,摸索过程还是花了些时间的,现在相关笔记分享给大家。 步骤 1、熟悉开发文档 熟悉飞书的开发文档:开发文档 ,找到你需要的接口,拿我为例,我需…...
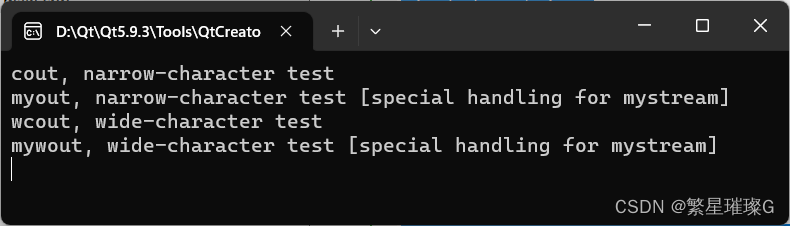
c++11 标准模板(STL)(std::ios_base)(三)
定义于头文件 <ios> class ios_base; 类 ios_base 是作为所有 I/O 流类的基类工作的多用途类。它维护数种数据: 1) 状态信息:流状态标志; 2) 控制信息:控制输入和输出序列格式化和感染的本地环境的标志; 3)…...
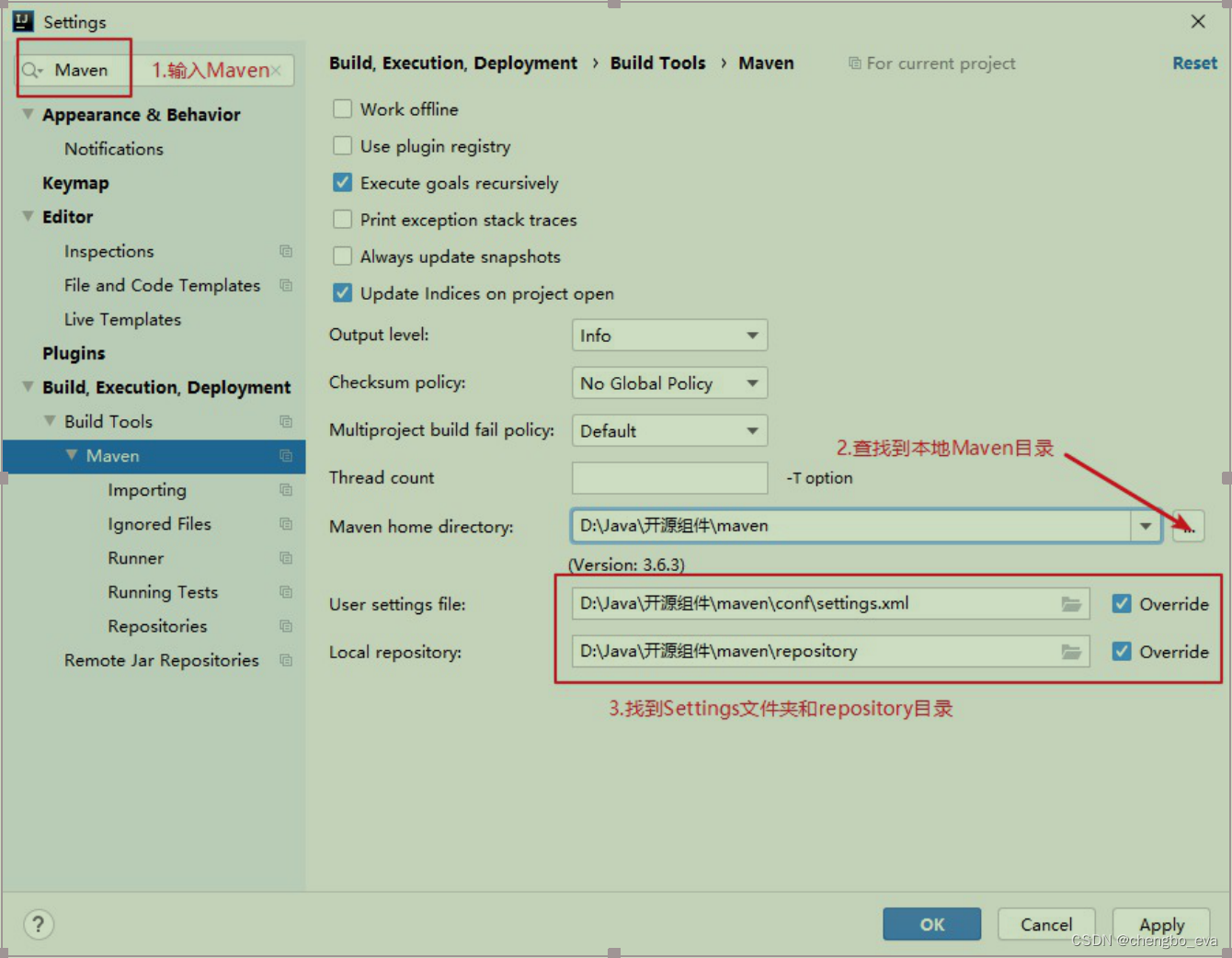
在线协同办公小程序开发搭建开发环境
目录 介绍 开发环境说明 虚拟机 原因 VirtualBox虚拟机 VMware虚拟机v15 安装MySQL数据库 安装步骤 导入EMOS系统数据库 安装MongoDB数据库 启动Navicat,选择创建MongoDB连接 创建用户 搭建Redis数据库 配置Maven 安装IDEA插件 Lombok插件 …...
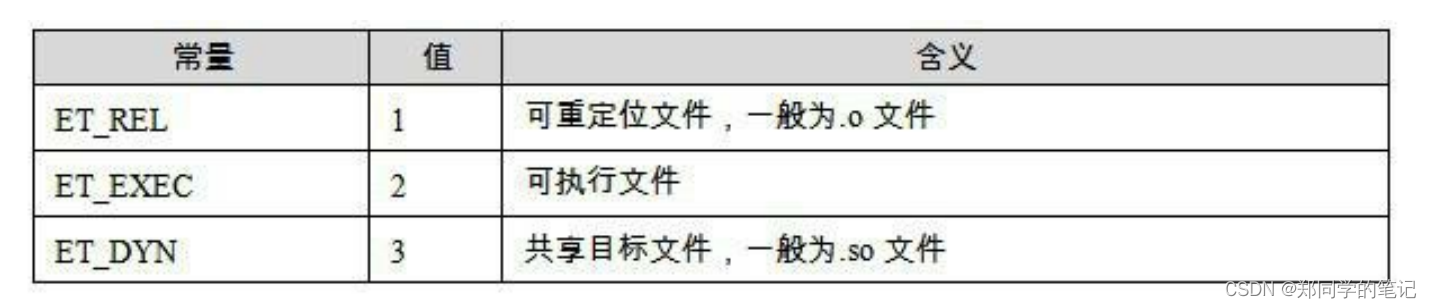
【编译、链接、装载六】汇编——目标文件
【编译和链接六】汇编——目标文件 一、目标文件_存储格式1、生成目标文件2、目标文件存储格式3、file查看文件格式 二、查看目标文件的内部结构——objdump三、代码段四、 数据段和只读数据段五、 ELF文件结构描述1、头文件2、段表2.1、重定位表2.2、字符串表2.3、查看重定位表…...
)
王道计算机考研408计算机组成原理汇总(下)
提示:真正的英雄是明白世界的残酷,也遭受了社会带给他的苦难,他依然能用心的说“我热爱这个世界,我愿竭尽所能去为我的世界而好好战斗 文章目录 前言4.1.1 指令格式4.1.2 扩展操作码指令格式4.2.1 指令寻址4.2.2 数据寻址4.2.3 偏移寻址4.2.4 堆栈寻址汇总前言4.3.1 高级语…...
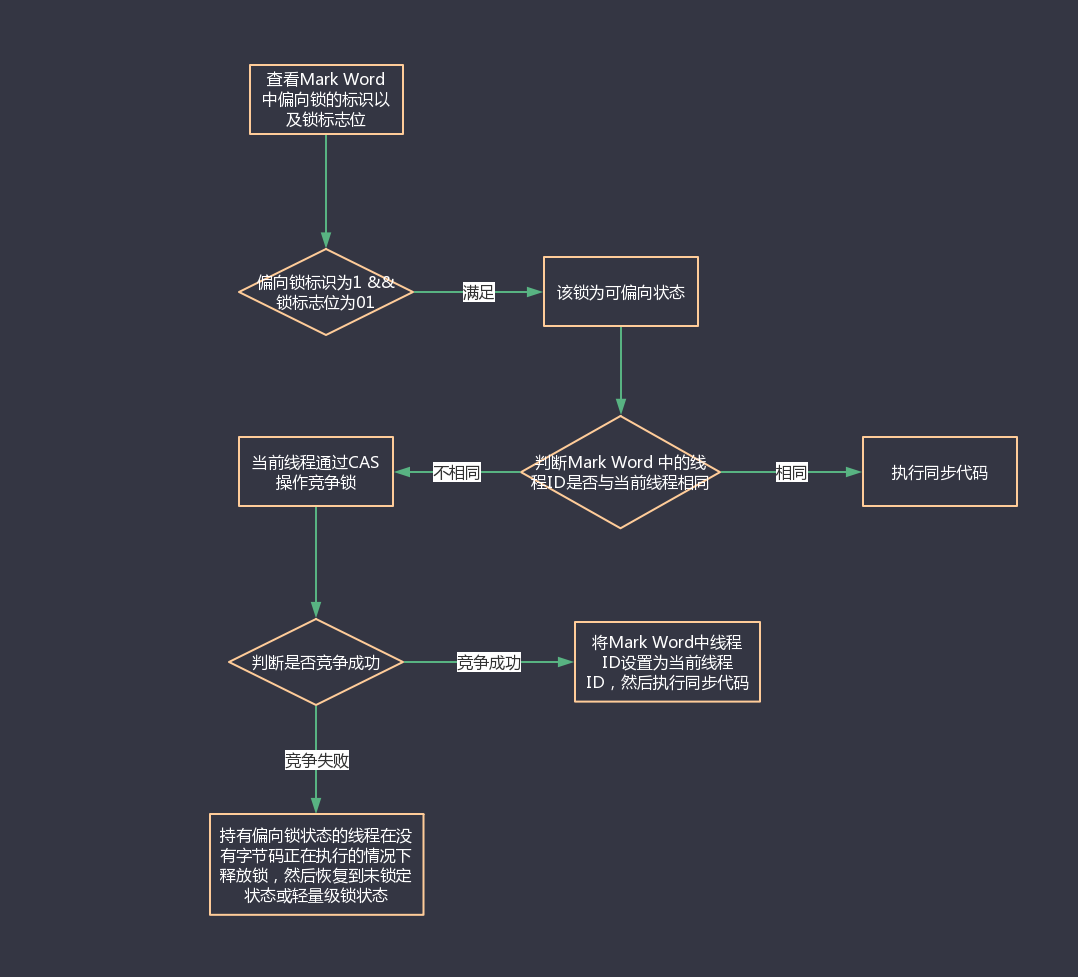
偏向锁、轻量级锁、重量级锁、自旋锁、自适应自旋锁
1. 偏向锁 偏向锁就是在运行过程中,对象的锁偏向某个线程。即在开启偏向锁机制的情况下,某个线程获得锁,当该线程下次再想要获得锁时,不需要重新申请获得锁(即忽略synchronized关键词),直接就可…...
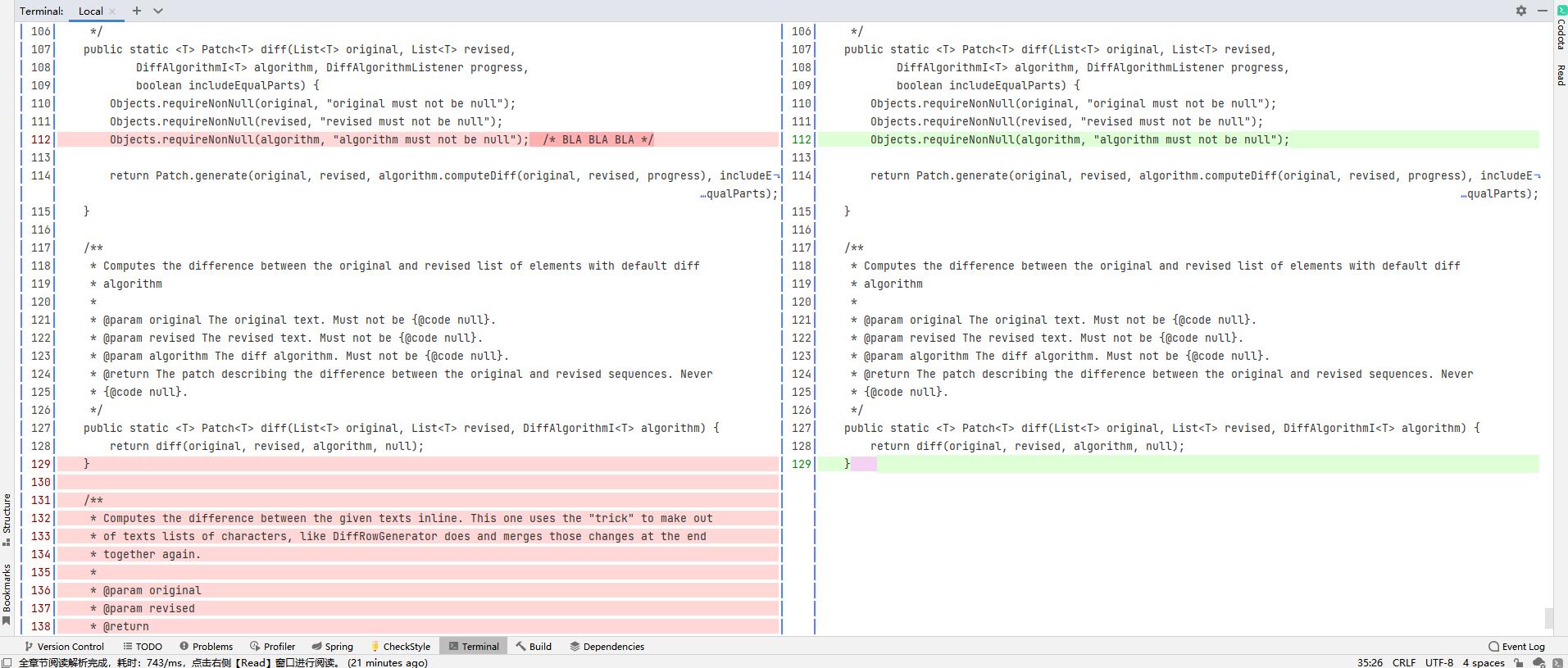
Delta 一个新的 git diff 对比显示工具
目录 介绍git diff 介绍delta介绍 一、安装1.下载 Git2.下载 delta3.解压4.修改配置文件5. 修改主题6.其他配置和说明 二、对比命令1.在项目中 git diff 常用命令2.对比电脑上两个文件3.对比电脑上的两个文件夹 三、在Git 命令行中使用效果四、在idea 的Terminal命令行中使用效…...

C# 二进制序列化和反序列化示例
.NET框架提供了两种种串行化的方式: 1、是使用BinaryFormatter进行串行化; 2、使用XmlSerializer进行串行化。 第一种方式提供了一个简单的二进制数据流以及某些附加的类型信息,而第二种将数据流格式化为XML存储。可以使用[Serializable]属…...

【CSS】文字扫光 | 渐变光
码来 可调整角度与颜色值来改变效果 <p class"gf-gx-color">我是帅哥</p> <style>.gf-gx-color {background: -webkit-linear-gradient(135deg,red,red 25%,red 50%,#fff 55%,red 60%,red 80%,red 95%,red);-webkit-text-fill-color: transparen…...

Overhaul Distillation(ICCV 2019)原理与代码解析
paper:A Comprehensive Overhaul of Feature Distillation official implementation:GitHub - clovaai/overhaul-distillation: Official PyTorch implementation of "A Comprehensive Overhaul of Feature Distillation" (ICCV 2019) 本文的…...
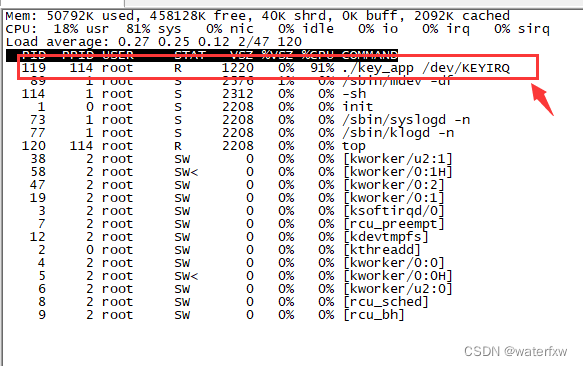
<Linux开发>驱动开发 -之-内核定时器与中断
<Linux开发>驱动开发 -之-内核定时器与中断 交叉编译环境搭建: <Linux开发> linux开发工具-之-交叉编译环境搭建 uboot移植可参考以下: <Linux开发> -之-系统移植 uboot移植过程详…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

C++ Saucer 编写Windows桌面应用
文章目录 一、背景二、Saucer 简介核心特性典型应用场景 三、生成自己的项目四、以Win32项目方式构建Win32项目禁用最大化按钮 五、总结 一、背景 使用Saucer框架,开发Windows桌面应用,把一个html页面作为GUI设计放到Saucer里,隐藏掉运行时弹…...
claude3.7高阶玩法,生成系统架构图,国内直接使用
文章目录 零、前言一、操作指南操作指导 二、提示词模板三、实战图书管理系统通过4o模型生成系统描述通过claude3.7生成系统架构图svg代码转换成图片 在线考试系统通过4o模型生成系统描述通过claude3.7生成系统架构图svg代码转换成图片 四、感受 零、前言 现在很多AI大模型可以…...


