Rust每日一练(Leetday0026) 最小覆盖子串、组合、子集

目录
76. 最小覆盖子串 Minimum Window Substring 🌟🌟🌟
77. 组合 Combinations 🌟🌟
78. 子集 Subsets 🌟🌟
🌟 每日一练刷题专栏 🌟
Rust每日一练 专栏
Golang每日一练 专栏
Python每日一练 专栏
C/C++每日一练 专栏
Java每日一练 专栏
76. 最小覆盖子串 Minimum Window Substring
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
- 对于
t中重复字符,我们寻找的子字符串中该字符数量必须不少于t中该字符数量。 - 如果
s中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = "ADOBECODEBANC", t = "ABC" 输出:"BANC"
示例 2:
输入:s = "a", t = "a" 输出:"a"
示例 3:
输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中, 因此没有符合条件的子字符串,返回空字符串。
提示:
1 <= s.length, t.length <= 10^5s和t由英文字母组成
进阶:你能设计一个在 o(n) 时间内解决此问题的算法吗?
代码1: 滑动窗口
use std::collections::HashMap;fn min_window(s: String, t: String) -> String {let s: Vec<u8> = s.into_bytes();let t: Vec<u8> = t.into_bytes();if s.len() < t.len() {return String::new();}let mut need: HashMap<u8, i32> = HashMap::new(); // 存储t中每个字符的出现次数for i in 0..t.len() {*need.entry(t[i]).or_insert(0) += 1;}let (mut left, mut right) = (0, 0); // 滑动窗口的左右指针let mut count = t.len(); // 记录滑动窗口中还需要的字符数let mut min_len = s.len() + 1; // 记录最小覆盖子串的长度let mut start = 0; // 记录最小覆盖子串的起始位置while right < s.len() {// 当右指针指向的字符是需要的字符,count减一if let Some(v) = need.get_mut(&s[right]) {if *v > 0 {count -= 1;}*v -= 1;}right += 1;// 当count为0时,说明滑动窗口中已经包含t中的所有字符while count == 0 {// 如果当前的覆盖子串更小,则更新最小覆盖子串的长度和起始位置if right - left < min_len {min_len = right - left;start = left;}// 当左指针指向的字符是需要的字符,count加一if let Some(v) = need.get_mut(&s[left]) {*v += 1;if *v > 0 {count += 1;}}left += 1;}}if min_len == s.len() + 1 {"".to_string()} else {String::from_utf8_lossy(&s[start..start + min_len]).to_string()}
}fn main() {println!("{}", min_window("ADOBECODEBANC".to_string(), "ABC".to_string()));println!("{}", min_window("a".to_string(), "a".to_string()));println!("{}", min_window("a".to_string(), "aa".to_string()));
}
代码2: 双指针
use std::collections::HashMap;fn min_window(s: String, t: String) -> String {let mut need: HashMap<char, i32> = HashMap::new();let mut count = t.len() as i32;let (mut left, mut right, mut start, mut min_len) = (0, 0, 0, s.len() + 1);for c in t.chars() {*need.entry(c).or_insert(0) += 1;}let s = s.chars().collect::<Vec<_>>();while right < s.len() {if let Some(v) = need.get_mut(&s[right]) {if *v > 0 {count -= 1;}*v -= 1;}right += 1;while count == 0 {if right - left < min_len {min_len = right - left;start = left;}if let Some(v) = need.get_mut(&s[left]) {*v += 1;if *v > 0 {count += 1;}}left += 1;}}if min_len == s.len() + 1 {"".to_owned() // 返回空字符串} else {s[start..start + min_len].iter().collect()}
}fn main() {println!("{}", min_window("ADOBECODEBANC".to_string(), "ABC".to_string()));println!("{}", min_window("a".to_string(), "a".to_string()));println!("{}", min_window("a".to_string(), "aa".to_string()));
}
输出:
BANC
a
//空行
77. 组合 Combinations
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2 输出: [[2,4],[3,4],[2,3],[1,2],[1,3],[1,4], ]
示例 2:
输入:n = 1, k = 1 输出:[[1]]
提示:
1 <= n <= 201 <= k <= n
代码1: 回溯法
fn combine(n: i32, k: i32) -> Vec<Vec<i32>> {let mut res: Vec<Vec<i32>> = vec![]; // 存储所有组合let mut path: Vec<i32> = vec![]; // 存储当前组合fn backtrack(start: i32, n: i32, k: i32, path: &mut Vec<i32>, res: &mut Vec<Vec<i32>>) {if path.len() == k as usize { // 当前组合长度为k,加入结果中res.push(path.clone());return;}for i in start..=n { // 枚举可选数字path.push(i); // 加入当前数字backtrack(i + 1, n, k, path, res); // 从i+1开始枚举下一个数字path.pop(); // 撤销当前数字}}backtrack(1, n, k, &mut path, &mut res); // 从1开始枚举第一个数字res
}fn main() {println!("{:?}", combine(4, 2));println!("{:?}", combine(1, 1));
}
输出:
[[1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]
[[1]]
代码2: 枚举法
fn combine(n: i32, k: i32) -> Vec<Vec<i32>> {let mut res: Vec<Vec<i32>> = vec![]; // 存储所有组合for i in 0..1<<n { // 枚举所有二进制数let mut path: Vec<i32> = vec![]; // 存储当前组合for j in 1..=n { // 枚举n个数字if i & 1 << j-1 != 0 { // 当前数字被选中path.push(j);}}if path.len() == k as usize { // 当前组合长度为k,加入结果中res.push(path);}}res
}fn main() {println!("{:?}", combine(4, 2));println!("{:?}", combine(1, 1));
}
78. 子集 Subsets
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3] 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0] 输出:[[],[0]]
提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10nums中的所有元素 互不相同
代码1:回溯法
fn subsets(nums: Vec<i32>) -> Vec<Vec<i32>> {let mut res: Vec<Vec<i32>> = vec![]; // 存储所有子集fn back_track (index: usize, path: &mut Vec<i32>, nums: &[i32], res: &mut Vec<Vec<i32>>) { // 递归枚举所有子集let tmp: Vec<i32> = path.to_vec(); // 将当前组合复制到临时数组中let n = nums.len();res.push(tmp); // 加入当前子集for i in index..n { // 枚举每个数字path.push(nums[i]); // 加入数字构成新的组合back_track (i+1, path, nums, res); // 递归枚举下一位数字path.pop(); // 移除数字}}back_track (0, &mut vec![], &nums, &mut res); // 从空集开始递归枚举所有子集res
}fn main() {let nums: Vec<i32> = vec![1, 2, 3];println!("{:?}", subsets(nums));let nums: Vec<i32> = vec![0];println!("{:?}", subsets(nums));
}输出:
[[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]
[[], [0]]
代码2: 循环枚举
fn subsets(nums: Vec<i32>) -> Vec<Vec<i32>> {let mut res: Vec<Vec<i32>> = vec![vec![]]; // 初始为空集for i in 0..nums.len() { // 枚举每个数字for sub in res.clone() { // 枚举已有的子集let mut temp = sub.clone();temp.push(nums[i]); // 加入当前数字res.push(temp); // 加入新的子集}}res
}fn main() {let nums: Vec<i32> = vec![1, 2, 3];println!("{:?}", subsets(nums));let nums: Vec<i32> = vec![0];println!("{:?}", subsets(nums));
}
输出:
[[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]
[[], [0]]
代码3: 位运算
fn subsets(nums: Vec<i32>) -> Vec<Vec<i32>> {let mut res: Vec<Vec<i32>> = vec![]; // 存储所有子集let n = nums.len();for i in 0..(1 << n) { // 枚举所有二进制数let mut path: Vec<i32> = vec![]; // 存储当前子集for j in 0..n { // 枚举n个数字if i & (1 << j) != 0 { // 当前数字被选中path.push(nums[j]);}}res.push(path); // 加入当前子集}res
}fn main() {let nums: Vec<i32> = vec![1, 2, 3];println!("{:?}", subsets(nums));let nums: Vec<i32> = vec![0];println!("{:?}", subsets(nums));
}输出:
[[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]
[[], [0]]
🌟 每日一练刷题专栏 🌟
✨ 持续,努力奋斗做强刷题搬运工!
👍 点赞,你的认可是我坚持的动力!
🌟 收藏,你的青睐是我努力的方向!
✎ 评论,你的意见是我进步的财富!
☸ 主页:https://hannyang.blog.csdn.net/
|
| Rust每日一练 专栏(2023.5.16~)更新中... |
|
| Golang每日一练 专栏(2023.3.11~)更新中... |
|
| Python每日一练 专栏(2023.2.18~2023.5.18)暂停更 |
|
| C/C++每日一练 专栏(2023.2.18~2023.5.18)暂停更 |
|
| Java每日一练 专栏(2023.3.11~2023.5.18)暂停更 |
相关文章:

Rust每日一练(Leetday0026) 最小覆盖子串、组合、子集
目录 76. 最小覆盖子串 Minimum Window Substring 🌟🌟🌟 77. 组合 Combinations 🌟🌟 78. 子集 Subsets 🌟🌟 🌟 每日一练刷题专栏 🌟 Rust每日一练 专栏 Gola…...

c# 从零到精通-ArrayList-Hashtable的操作
c# 从零到精通-ArrayList-Hashtable的操作 1、ArrayList的操作 using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Collections; namespace Test11 { class Program { static void Main(string[] args) { ArrayList list …...

pnpm带来了什么
首先 pnpm 和 npm yarn 一样是包管理工具,他解决了npm 和 yarn 存在的一些问题 npm3之前每个依赖都是一层嵌套一层的,每个依赖里都有node_modules 用来存放依赖所需的依赖包导致重复下载的依赖包很多,一层层嵌套,嵌套很深&#x…...
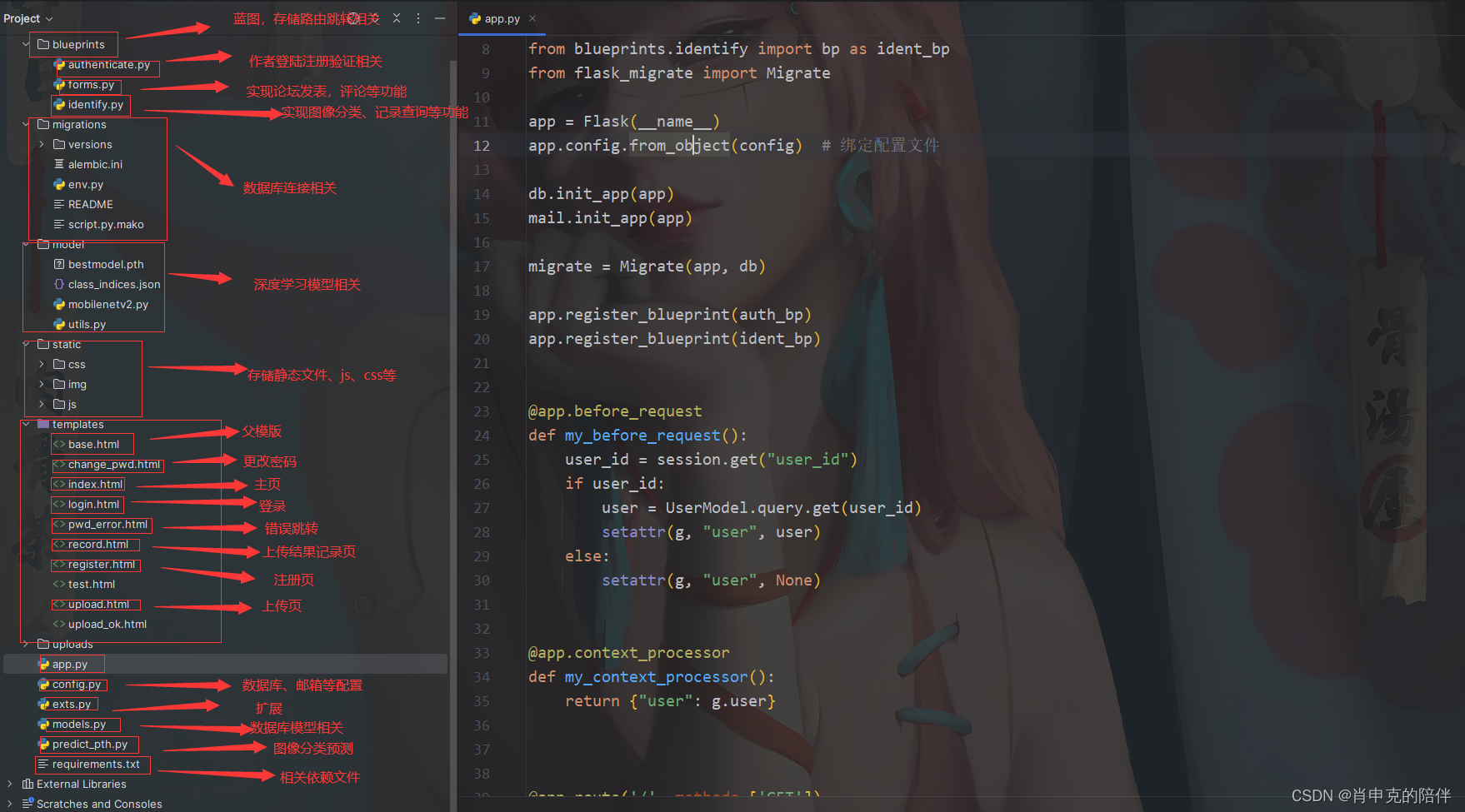
图像分类模型嵌入flask中开发PythonWeb项目
图像分类模型嵌入flask中开发PythonWeb项目 图像分类是一种常见的计算机视觉任务,它的目的是将输入的图像分配到预定义的类别中,如猫、狗、花等。图像分类模型是一种基于深度学习的模型,它可以利用大量的图像数据来学习图像的特征和类别之间…...
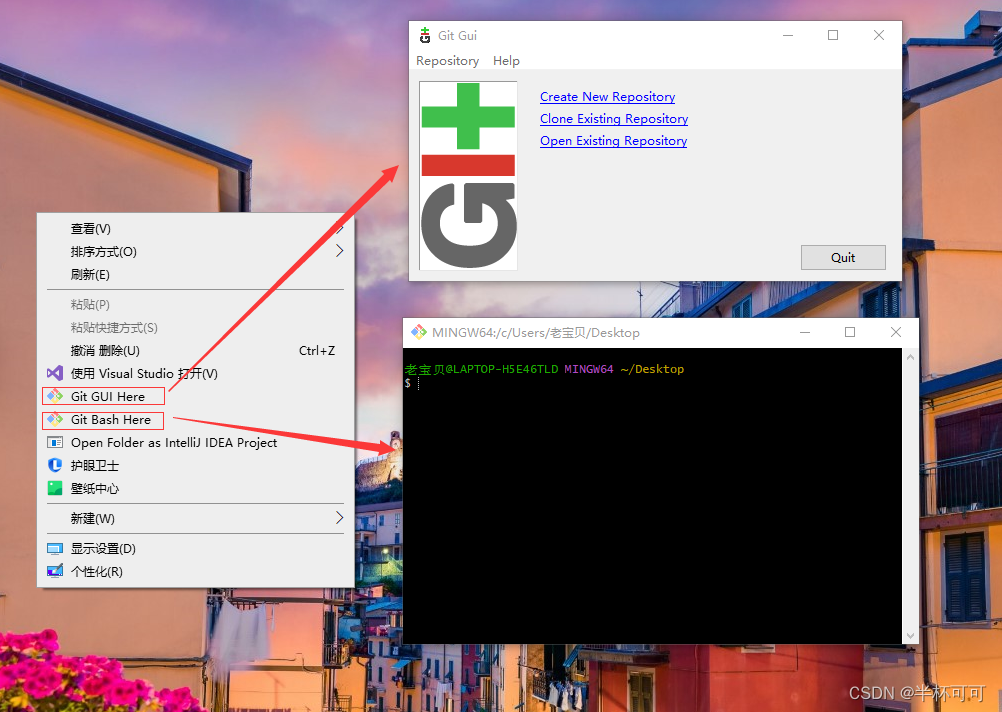
GIT安装教程(入门)
目录 前言 Git作者 官网 GIT优点 GIT缺点 为什么要使用 Git 下载以及安装步骤 一、官网下载 二、GIT安装步骤 1、安装get程序 2、许可声明 3、选择安装路径 4、选择git组件 5、创建菜单名称 6、 git文件默认编辑器 7、设置新存储库中初始分支的名称 8、调整Pa…...

全志V3S嵌入式驱动开发(触摸屏驱动)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 所谓的触摸屏,其实就是在普通的lcd屏幕之上,再加一层屏而已。这个屏是透明的,这样客户就可以看到下面lcd屏幕的…...

死信队列详解
什么是死信队列? 在消息队列中,执行异步任务时,通常是将消息生产者发布的消息存储在队列中,由消费者从队列中获取并处理这些消息。但是,在某些情况下,消息可能无法正常地被处理和消耗,例如&…...
:北京卷I)
我用ChatGPT写2023高考语文作文(五):北京卷I
2023年 北京卷 I 适用地区:北京 “续航”一词,原指连续航行,今天在使用中被赋予了新的含义,如为青春续航、科技为经济发展续航等。 请以“续航”为题目,写一篇议论文。 要求:论点明确,论据充实&…...
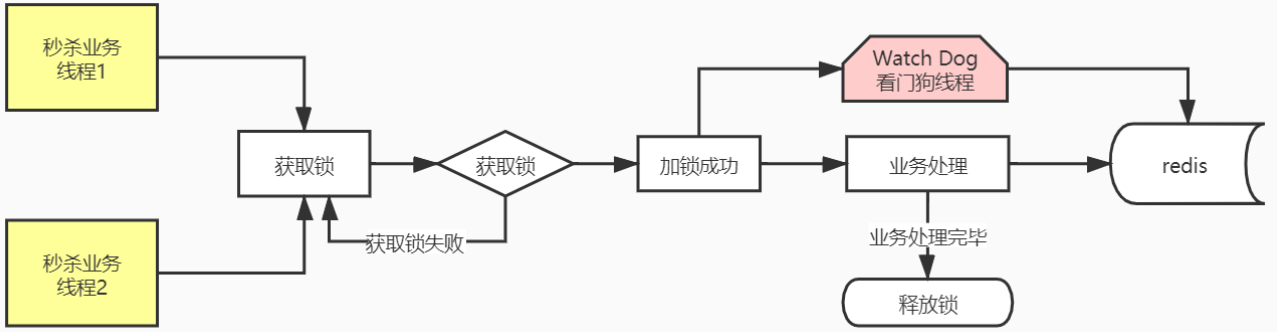
《微服务实战》 第二十八章 分布式锁框架-Redisson
前言 Redisson 在基于 NIO 的 Netty 框架上,充分的利⽤了 Redis 键值数据库提供的⼀系列优势,在Java 实⽤⼯具包中常⽤接⼝的基础上,为使⽤者提供了⼀系列具有分布式特性的常⽤⼯具类。使得原本作为协调单机多线程并发程序的⼯具包获得了协调…...

局部搜索,变邻域搜索算法
目录 局部搜索 02 变邻域搜索算法 局部搜索 1.1 局部搜索是什么玩意儿? 官方一点:局部搜索是解决优化问题的一种启发式算法。对于某些计算起来非常复杂的优化问题,比如各种NP-难问题,要找到最优解需要的时间随问题规模呈指数增长,因此诞生了各种启发式算法来退而求其次…...

软件工程实训——第一天
第一天 前后分离 前端:android 后端:springbootmbatis-plus 高心星 软件工程的思维来开发项目 问题定义 可行性研究 需求分析 概要设计 详细设计 编码 测试 维护 需求分析 1.用户的信息管理 2.新增支出 3.新增收入 4.支出统计 5.收入…...
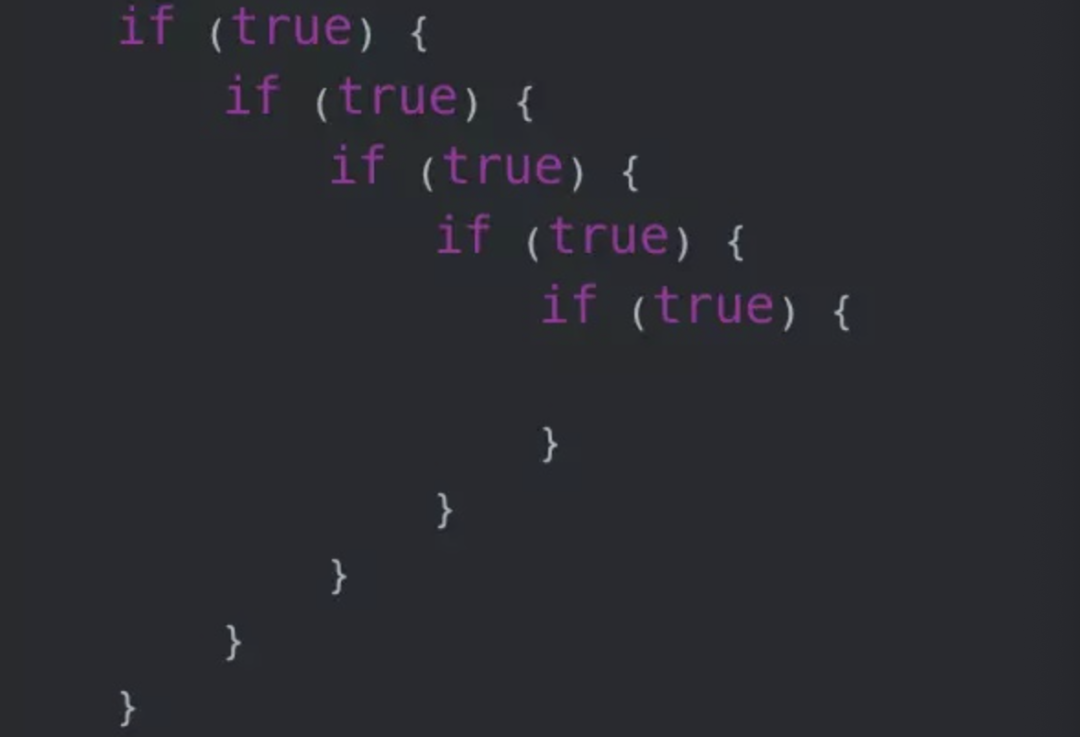
嵌入式C语言中if/else如何优化详解
观点一(灵剑): 前期迭代懒得优化,来一个需求,加一个if,久而久之,就串成了一座金字塔。 当代码已经复杂到难以维护的程度之后,只能狠下心重构优化。那,有什么方案可以优雅…...

【LSTM】读取时间序列数据 | 时间序列数据的小批量划分方法
由于序列数据本质上是连续的,因此我们在处理数据时需要解决这个问题。当序列过长而不能被模型一次性全部处理时,我们希望能拆分这样的序列以便模型方便读取。 Q:怎样随机生成一个具有n个时间步的mini batch的特征和标签? A&…...
K8s in Action 阅读笔记——【12】Securing the Kubernetes API server
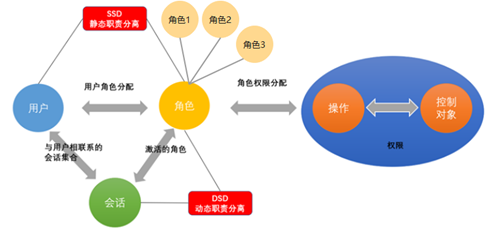
K8s in Action 阅读笔记——【12】Securing the Kubernetes API server 12.1 Understanding authentication 在上一章中,我们提到API服务器可以配置一个或多个认证插件(授权插件也是同样的情况)。当API服务器接收到一个请求时,它…...
爆肝整理,3个月从功能进阶自动化测试,一跃成测试卷王...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 首先先了解自动化…...

人生这场概率游戏,怎么玩
只会标准答案,是不可救药的愚蠢 那么为了便于理解,我用一些典型的案例来讲解,什么是概率游戏,以及这个游戏,应该怎么玩。 比如典型的相亲,婚恋。人生大事,用标准答案来说,你的意中人…...
Redis笔记
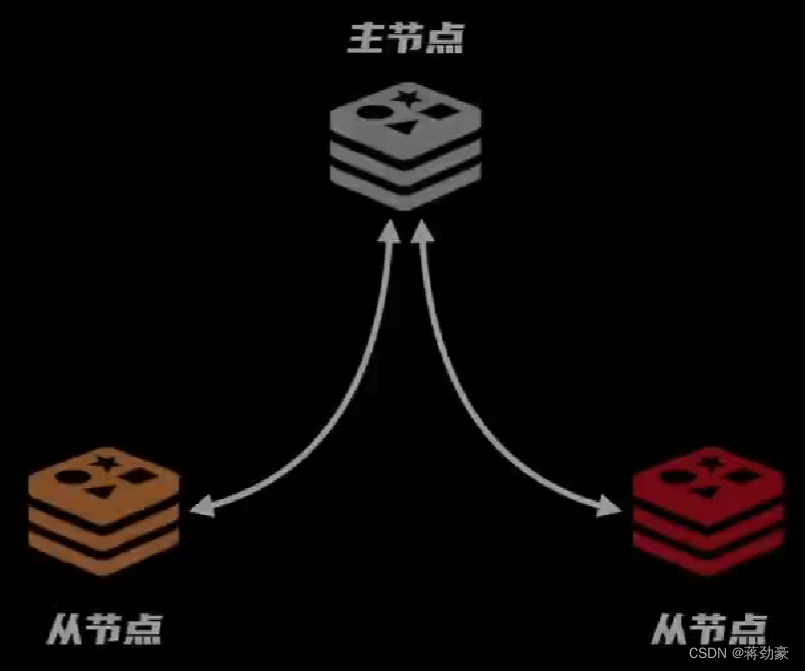
缓存过期时间很重要!redis是单线程的 对于内存过多的3中方案: 惰性删除: 在定时删除的基础上,对于已经过期了的数据,redis的随机选择算法一直没有选中这个数据,所以导致它就一直没被删除,但是…...

centos 安装supervisor并运行网站
前言 之前一直用宝塔的**进程守护管理器【Supervisor】**来启动一些项目,如ThinkPHP、Hyperf的项目,或laravel的一些命令。如果不用宝塔怎么办呢? 一、简介[supervisor] [Supervisor] 是用Python开发的一个client/server服务,是Linux/Unix系统下的一个进程管理工具,不支…...

Hadoop面试题十道
问题 1:Hadoop是什么? 答案:Hadoop是一个开源的分布式计算框架,用于处理大规模数据集的存储和处理。它基于Google的MapReduce和Google文件系统(GFS)的思想,旨在解决大数据量的处理和分析问题。…...
使用Docker-Compose对Docker容器集群快速编排
目录 一、Docker-Compose1、Docker-Compose使用场景2、Docker-Compose简介3、Docker-Compose安装部署4、YAML 文件格式及编写注意事项5、Docker Compose配置常用字段6、Docker Compose 常用命令7、Docker Compose 文件结构8、docker Compose撰写nginx 镜像9、docker Compose撰写…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...




