【人工智能】— 逻辑回归分类、对数几率、决策边界、似然估计、梯度下降
【人工智能】— 逻辑回归分类、对数几率、决策边界、似然估计、梯度下降
- 逻辑回归分类
- Logistic Regression Classification
- Logistic Regression: Log Odds
- Logistic Regression: Decision Boundary
- Likelihood under the Logistic Model
- Training the Logistic Model
- Gradient Descent
逻辑回归分类
考虑二分类问题,其中每个样本由一个特征向量表示。
直观理解:将特征向量 x \text{x} x映射到一个实数 w T x \text{w}^T\text{x} wTx
- 一个正的值 w T x \text{w}^T\text{x} wTx表示 x \text{x} x属于正类的可能性较高。
- 一个负的值 w T x \text{w}^T\text{x} wTx表示 x \text{x} x属于负类的可能性较高。
概率解释: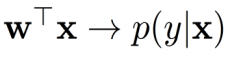
- 对映射值应用一个变换函数,将其范围压缩在0和1之间。
- 变换后的值表示属于正类的概率。
- 变换后的值 w T x ∈ ( − ∞ , + ∞ ) \text{w}^T\text{x}\in(-∞,+∞) wTx∈(−∞,+∞)的范围是 [ 0 , 1 ] [0, 1] [0,1]。
注意:在逻辑回归中通常使用的变换函数是sigmoid函数。
Logistic Regression Classification
条件概率:
- 条件概率在分类任务中很重要。
- 使用逻辑函数(也称为sigmoid函数)计算条件概率。
逻辑函数 / sigmoid函数:
-
当 z 趋近正无穷时,逻辑函数趋近于1。
-
当 z 趋近负无穷时,逻辑函数趋近于0。
-
当 z = 0 时,逻辑函数等于0.5,表示两个类别的概率相等。
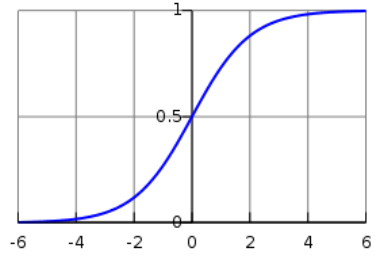
-
给定输入 x,正类的概率表示为:
p ( y = 1 ∣ x ) = σ ( w T x ) = 1 1 + e − w T x = e w T x 1 + e w T x p(y = 1 \,|\, x) =\sigma(w^Tx) = \cfrac{1}{1 + e^{-w^T x}} = \cfrac{e^{w^T x}}{1 + e^{w^T x}} p(y=1∣x)=σ(wTx)=1+e−wTx1=1+ewTxewTx -
给定输入 x,负类的概率表示为:
p ( y = 0 ∣ x ) = 1 − p ( y = 1 ∣ x ) = 1 1 + e w T x p(y = 0 \,|\, x) = 1 - p(y = 1 \,|\, x) = \cfrac{1}{1 + e^{w^T x}} p(y=0∣x)=1−p(y=1∣x)=1+ewTx1
Logistic Regression: Log Odds
- 在逻辑回归中,我们使用log odds(对数几率)来建模。
- 一个事件的几率(odds):该事件发生的概率与不发生的概率的比值, p 1 − p \cfrac{p}{1-p} 1−pp。
- log odds / logit function: log ( p 1 − p ) \log\left(\cfrac{p}{1-p}\right) log(1−pp)。
- Log odds for logistic regression: log ( p ( y = 1 ∣ x ) 1 − p ( y = 1 ∣ x ) ) = w T x \log\left(\cfrac{p(y=1|x)}{1-p(y=1|x)}\right) = w^Tx log(1−p(y=1∣x)p(y=1∣x))=wTx。
在逻辑回归中,我们通过学习适当的权重 w w w 来建立一个线性模型,该模型可以将输入特征 x x x 映射到对数几率(log odds)上。然后,通过对对数几率应用逻辑函数(sigmoid函数)来得到分类概率。
Logistic Regression: Decision Boundary
决策边界: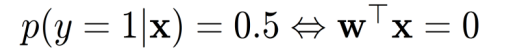
- 在逻辑回归中,决策边界是指分类模型对于输入特征的判断边界。
- 对于线性逻辑回归模型,决策边界是线性的。
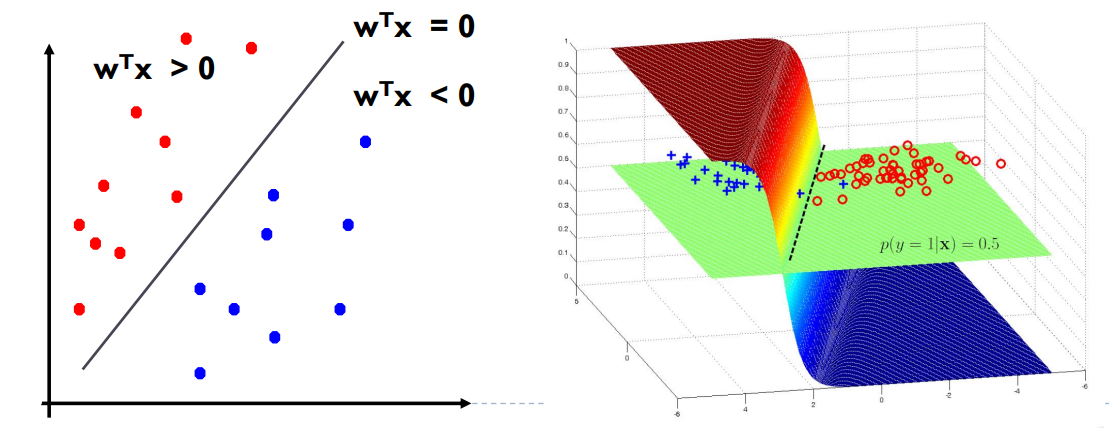
决策规则:
- 如果 p ^ ( y = 1 ∣ x ) ≥ 0.5 \hat{p}(y=1|x) \geq 0.5 p^(y=1∣x)≥0.5,则预测为正类。
- 如果 p ^ ( y = 1 ∣ x ) < 0.5 \hat{p}(y=1|x) < 0.5 p^(y=1∣x)<0.5,则预测为负类。
对于线性逻辑回归,决策边界是一个线性函数,用于将特征空间划分为两个不同的类别区域。
Likelihood under the Logistic Model
在逻辑回归中,我们观察标签并测量它们在模型下的概率。
给定参数 w w w,样本的条件对数似然函数为:
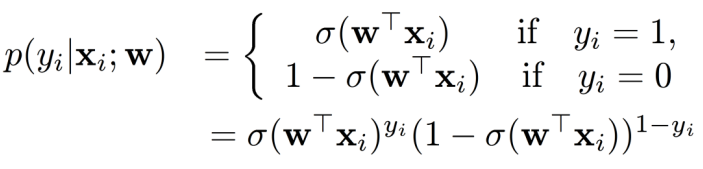
对数似然函数的表达式为:
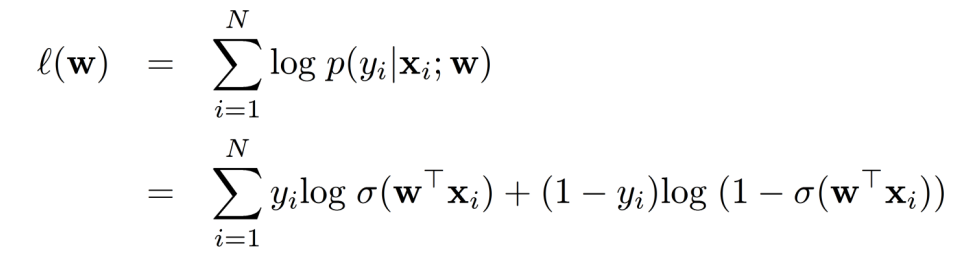
其中, N N N 是样本数量, x i x_i xi 是第 i i i 个样本的特征向量, y i y_i yi 是第 i i i 个样本的标签。
通过最大化对数似然函数来估计参数 w w w,可以找到最佳的参数值,使得模型的概率预测与观察到的标签尽可能一致。
Training the Logistic Model
训练逻辑回归模型(即找到参数 w w w)可以通过最大化训练数据的条件对数似然函数或最小化损失函数来完成。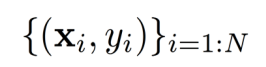
最大化条件对数似然函数 or 最小化损失函数:
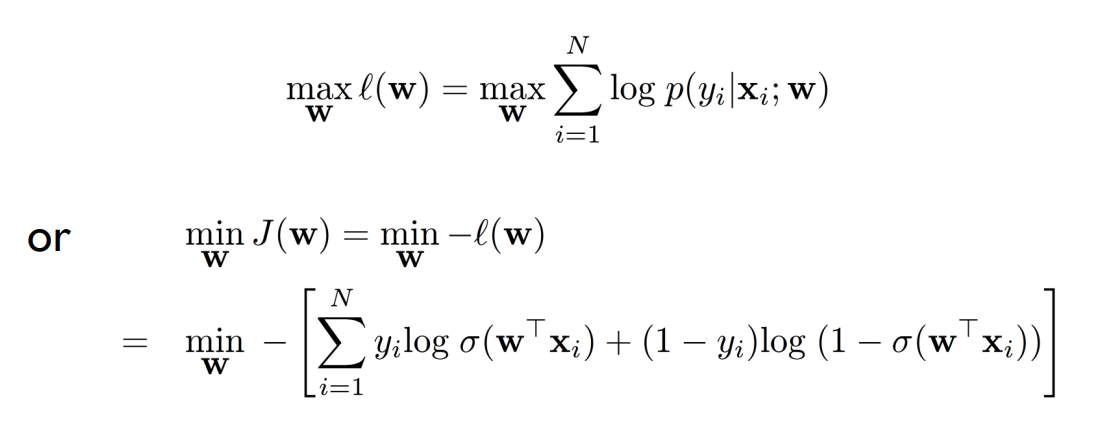
其中, N N N 是训练数据的样本数量, x i x_i xi 是第 i i i 个样本的特征向量, y i y_i yi 是第 i i i 个样本的标签。
通过最大化条件对数似然函数或最小化损失函数,我们可以找到最优的参数 w w w,使得模型能够最好地拟合训练数据,并能够准确地预测新的样本标签。常用的优化算法,如梯度下降法或牛顿法,可以用于求解最优参数。
Gradient Descent
梯度下降是一种常用的优化算法,用于求解最小化损失函数的问题。
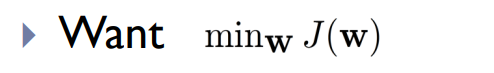
梯度下降的步骤如下:
- 初始化参数 w w w 的值。
- 重复以下步骤直到满足停止条件:
- 计算损失函数 J ( w ) J(w) J(w) 对参数 w w w 的梯度,即 ∂ J ( w ) ∂ w \cfrac{\partial J(w)}{\partial w} ∂w∂J(w)。
- 根据学习率 α \alpha α,更新参数 w w w 的值: w j : = w j − α ∂ J ( w ) ∂ w j w_j := w_j - \alpha \cfrac{\partial J(w)}{\partial w_j} wj:=wj−α∂wj∂J(w),对所有参数 w j w_j wj 同时进行更新。
梯度下降的目标是通过迭代更新参数,逐渐减小损失函数的值,直到达到局部最小值或收敛。
在逻辑回归中,我们可以使用梯度下降算法来最小化损失函数 J ( w ) J(w) J(w),从而找到最优的参数 w w w,使得模型能够最好地拟合训练数据。通过计算损失函数对参数的梯度,然后根据梯度和学习率更新参数,我们可以逐步调整参数的值,使得损失函数逐渐减小,从而达到最优参数的目标。
相关文章:
【人工智能】— 逻辑回归分类、对数几率、决策边界、似然估计、梯度下降
【人工智能】— 逻辑回归分类、对数几率、决策边界、似然估计、梯度下降 逻辑回归分类Logistic Regression ClassificationLogistic Regression: Log OddsLogistic Regression: Decision BoundaryLikelihood under the Logistic ModelTraining the Logistic ModelGradient Desc…...

k8s pod “cpu和内存“ 资源限制
转载用于收藏学习:原文 文章目录 Pod资源限制requests:limits:docker run命令和 CPU 限制相关的所有选项如下: Pod资源限制 为了保证充分利用集群资源,且确保重要容器在运行周期内能够分配到足够的资源稳定运行&#x…...
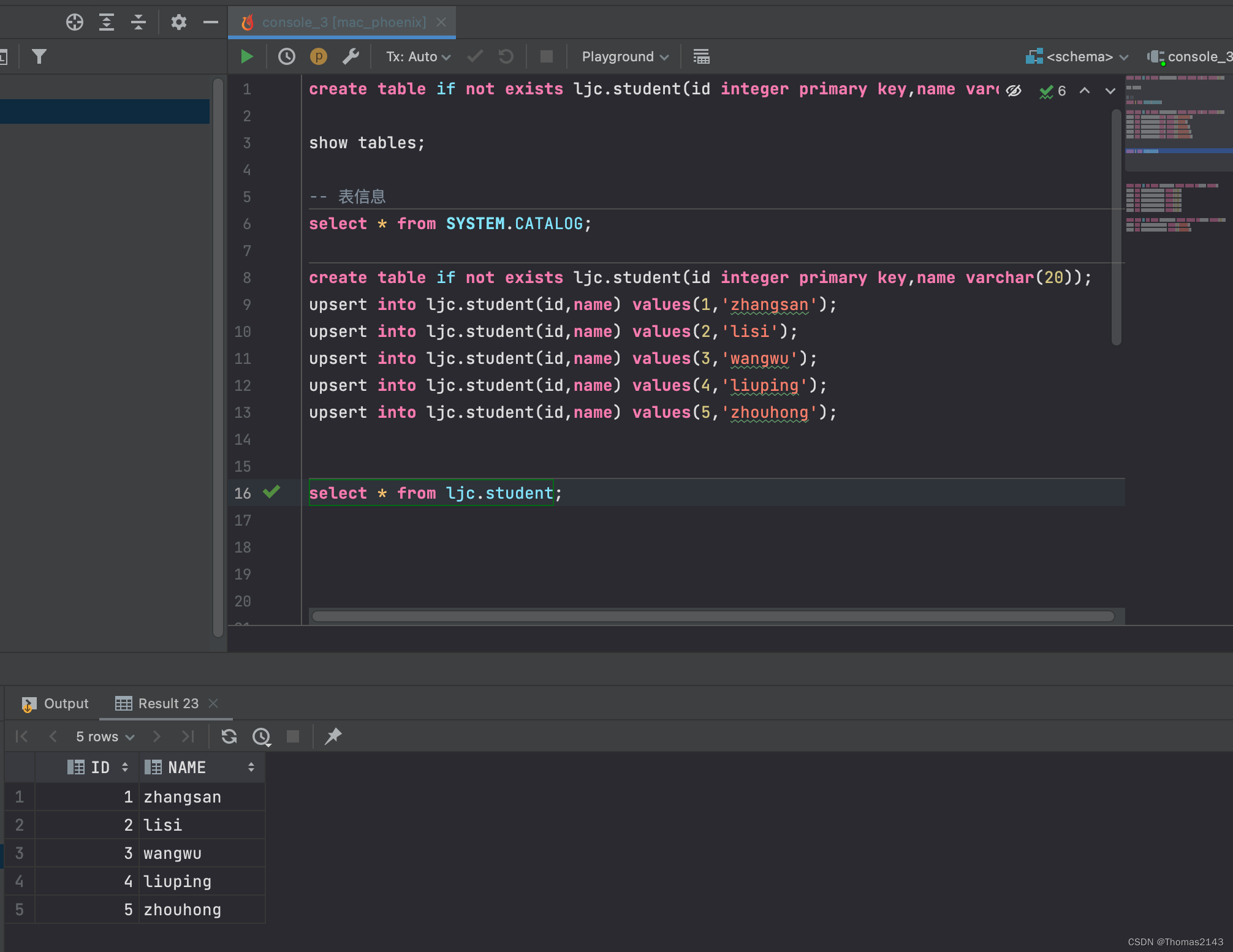
datagrip 连接 phoenix
jar替换完后尽量重启datagrip. 然后重新连接即可. 不重启貌似报错... 效果:...

黑客入侵的常法
1.无论什么站,无论什么语言,我要渗透,第一件事就是扫目录,最好一下扫出个上传点,直接上传 shell ,诸位不要笑,有时候你花很久搞一个站,最后发现有个现成的上传点,而且很容…...
)
VB报警管理系统设计(源代码+系统)
可定时显示报警系统是一个能够定时并及时报警,提醒人们安全有效地按计划完成任务的系统。本论文从软件工程的角度,对可定时显示报警系统做了全面的需求分析,简要说明了该系统的构思、特点及开发环境;阐述了系统的主要功能,论述了它的设计与实现,并且叙述了系统的测试与评…...
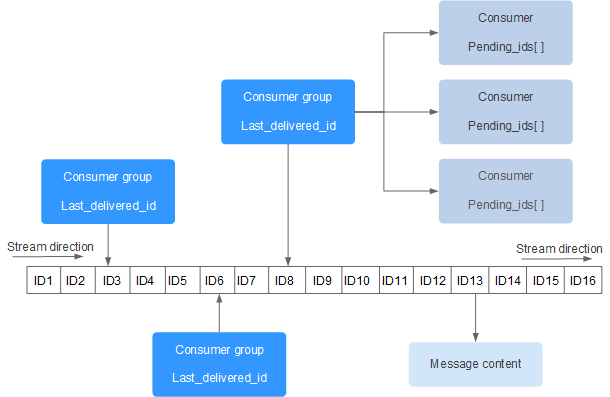
Redis入门 - Redis Stream
原文首更地址,阅读效果更佳! Redis入门 - Redis Stream | CoderMast编程桅杆Redis入门 - Redis Stream Redis Stream 是 Redis 5.0 版本新增加的数据结构。 Redis Stream 主要用于消息队列(MQ,Message Queue)…...

微服务中常见问题
Spring Cloud 组件 Spring Cloud五大组件有哪些? Eureka:注册中心 Ribbon:负载均衡 Feign:远程调用 Hystrix:服务熔断 Zuul/Gateway:服务网关 随着SpringCloud Alibaba在国内兴起,我们项目中…...

更新删除清理购物车
目录 1 更新购物车 2 取会员门店购物车项 3 取会员门店购物车项(无缓存) 4 删除门店购物车某项 5 删除门店购物车多项 6 清理门店购物车 7 清理门店购物车 8 添加商品至购物车 9 添加商品至购物车...

基于Intel NUC平台的字符设备陀螺仪GX5-25驱动程序
陀螺仪GX5-25连接到Intel NUC上可能需要进行一些设备树的修改和编写驱动程序的工作。这是因为陀螺仪GX5-25可能需要特定的设备树配置和驱动程序来与Intel NUC的硬件和操作系统进行通信。 如果陀螺仪GX5-25没有官方的Linux驱动程序或文档,您可能需要自己编写驱动程序…...
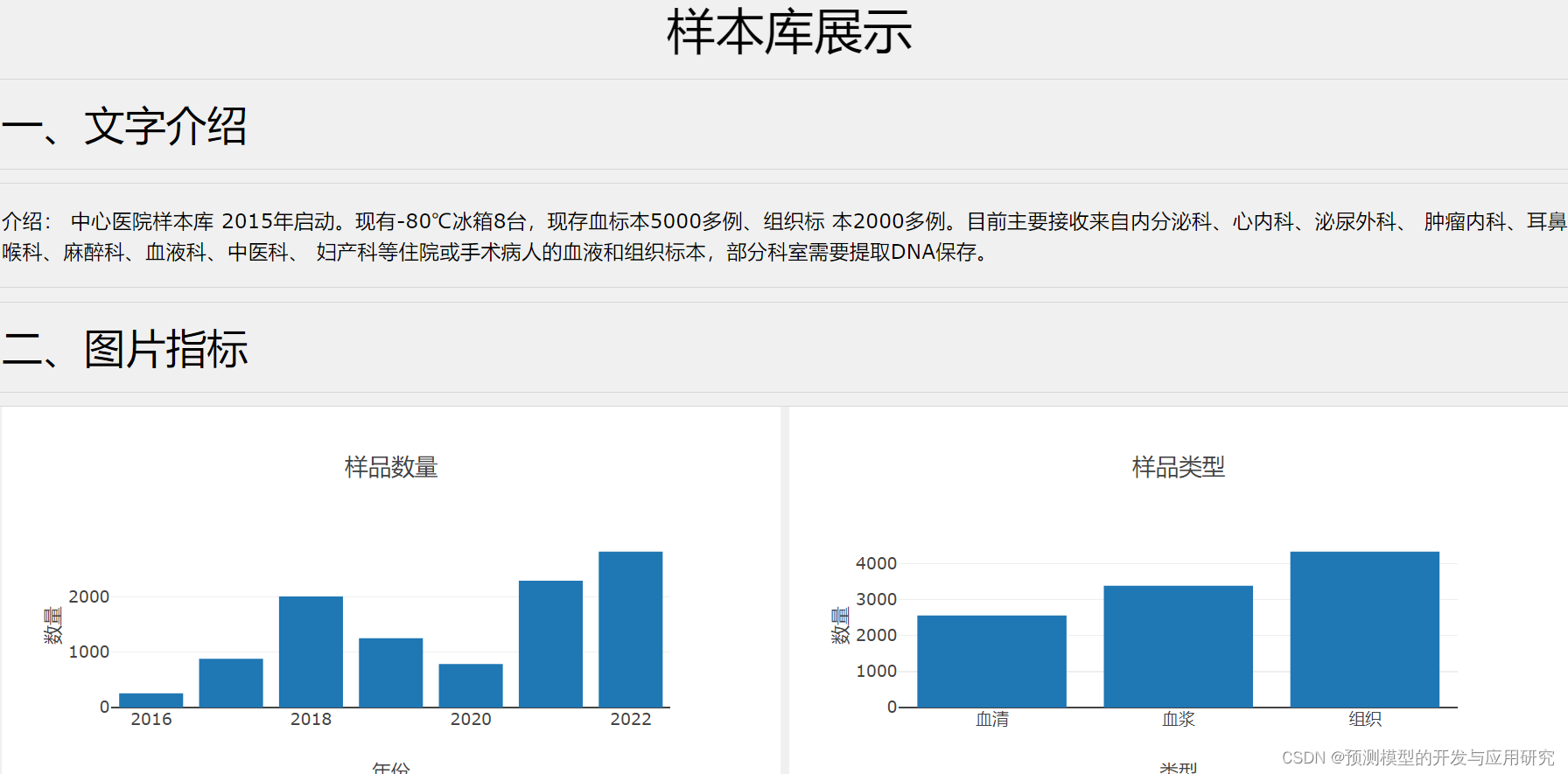
建立小型医学数据库(总结)
建立小型医学数据库 小型医学数据库可以用于存储和管理医学数据,如患者病历、药品信息、试验结果等。这对于医疗机构和科研机构来说非常必要,可以提高数据管理和共享的效率,进而促进医学研究和诊疗水平的提升。 建立小型医学数据库有以下基本…...

Git学习笔记
文章目录 一. 引入1. SCM软件2. 概念 二. GitHubDesktop三. Git1. 版本号 (底层原理)1.1 视频笔记1.2 实操记录 2. Git命令2.0 汇总2.1 仓库操作2.2 文件操作2.3 分支操作2.4 标签操作2.5 远程仓库 四. idea操作 一. 引入 1. SCM软件 2. 概念 集中式版本控制 文件冲突 可以上…...

vue面试题1. 请说下封装 vue 组件的过程?2. Vue组件如何进行传值的?3. Vue 组件 data 为什么必须是函数?4. 讲一下组件的命名规范
1. 请说下封装 vue 组件的过程? 首先,组件可以提升整个项目的开发效率。能够把页面抽象成多个相对独立的模块,解决了我们传统项目开发:效率低、难维护、复用性等问题。 分析需求:确定业务需求,把页面中可以…...

Docker使用记录
文章目录 Docker基本使用Docker配置查看状态卸载安装使用 apt 存储库安装在 Ubuntu 上安装 Docker 桌面(非必要) Docker实例使用现有的镜像查找镜像拖取镜像列出镜像列表更新镜像导出镜像删除镜像导入镜像清理镜像查看容器导出容器导入容器-以镜像的方式创建容器重启容器进入容…...
OpenCV(图像处理)-基于Python-形态学处理-开运算、闭运算、顶帽、黑帽运算
1. 形态学2. 常用接口2.1 cvtColor()2.2 图像二值化threshod()自适应阈值二值化adaptiveThreshod() 2.3 腐蚀与膨胀erode()getStructuringElement()dilate() 2.4开、闭、梯度、顶帽、黑帽运算morphologyEx() 1. 形态学 OpenCV形态学是一种基于OpenCV库的数字图像处理技术&…...

chatgpt赋能python:Python支持跨平台软件开发
Python支持跨平台软件开发 作为一种高级编程语言,Python 以其丰富的库和跨平台支持而备受开发人员欢迎。Python 通过将应用程序的可移植性最大化,使得开发人员可以轻松地在不同的操作系统平台上构建和部署软件。 跨平台支持 Python 支持各种不同的操作…...
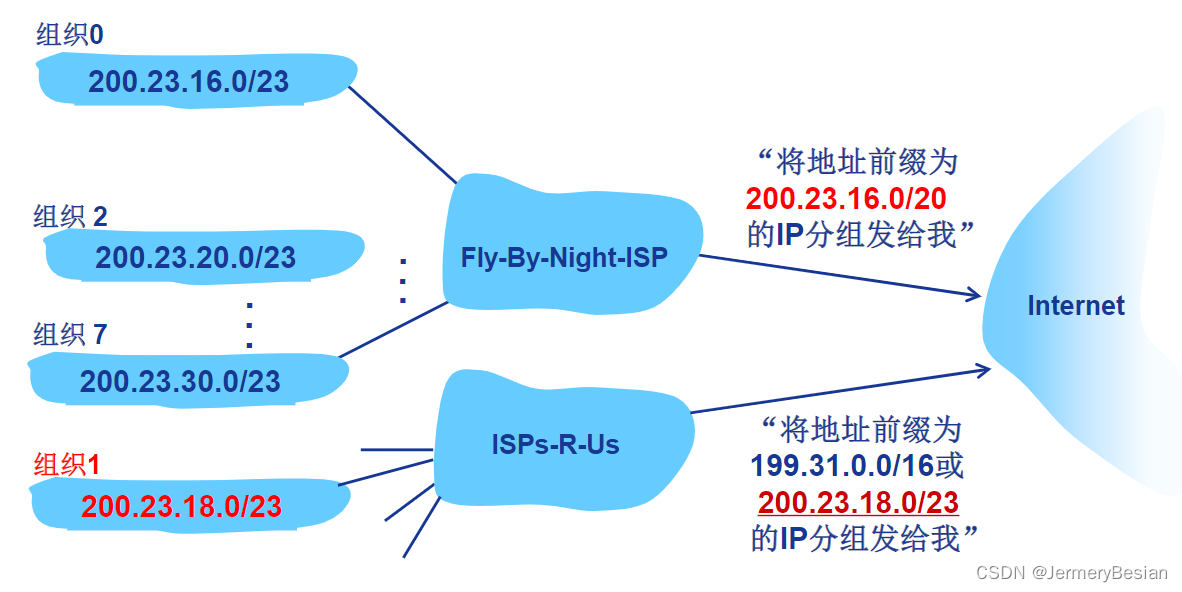
哈工大计算机网络课程网络层协议详解之:CIDR与路由聚集
哈工大计算机网络课程网络层协议详解之:CIDR与路由聚集 文章目录 哈工大计算机网络课程网络层协议详解之:CIDR与路由聚集CIDR与路由聚集CIDR路由聚集 CIDR与路由聚集 CIDR CIDR:无类域间路由(CIDR:Classless InterDo…...
——日期 时间)
C++ 教程(19)——日期 时间
C 日期 & 时间 C 标准库没有提供所谓的日期类型。C 继承了 C 语言用于日期和时间操作的结构和函数。为了使用日期和时间相关的函数和结构,需要在 C 程序中引用 <ctime> 头文件。 有四个与时间相关的类型:clock_t、time_t、size_t 和 tm。类型…...
React 应用 Effect Hook 函数式中操作生命周期
React Hook入门小案例 在函数式组件中使用state响应式数据给大家演示了最简单的 Hook操作 那么 我们继续 首先 Hook官方介绍 他没有破坏性是完全可选的 百分比兼容 也就说 我们一起的 类 class的方式也完全可以用 只要 react 16,8以上就可以使用 Hook本身不会影响你的react的理…...

C代码程序实现扫雷游戏纯代码版本
//test.c文件 #define _CRT_SECURE_NO_WARNINGS 1#include "game.h"void menu() {printf("***********************\n");printf("***** 1. play *****\n");printf("***** 0. exit *****\n");printf("*******************…...

ai代写---怎么在ubutnu服务器中安装mqtt
在Ubuntu服务器中安装MQTT Broker可以使用Mosquitto,它是一个开源的MQTT Broker实现,支持Linux、Windows和MacOS等多个平台。 以下是在Ubuntu服务器中安装Mosquitto的步骤: 更新apt-get包列表 打开终端,执行以下命令更新apt-get…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
