动态规划part9 | ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III
文章目录
- 198.打家劫舍
- 思路
- 思路代码
- 官方题解
- 代码
- 213.打家劫舍II
- 思路
- 思路代码
- 官方代码
- 困难
- 337.打家劫舍III
- 思路
- 思路代码
- 官方题解
- 代码
- 困难
- 今日收获
198.打家劫舍
198.打家劫舍
思路
dp含义,偷前i个房,切第i个房偷
dp[i]=max(dp[i-2],dp[i-3])+nums[i]
所以结果为
max(dp[len(nums)-1],dp[len(nums)-2])
思路代码
func rob(nums []int) int {if len(nums)==1{return nums[0]}if len(nums)==2{return max(nums[0],nums[1])}dp:=make([]int,len(nums))dp[0]=nums[0]dp[1]=max(nums[0],nums[1])dp[2]=max(nums[1],dp[0]+nums[2])for i:=3;i<len(nums);i++{dp[i]=max(dp[i-2],dp[i-3])+nums[i]}return max(dp[len(nums)-1],dp[len(nums)-2])
}func max(i,j int)int{if i<j{return j}return i
}
官方题解
确定dp数组(dp table)以及下标的含义
dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]。
确定递推公式
决定dp[i]的因素就是第i房间偷还是不偷。
如果偷第i房间,那么dp[i] = dp[i - 2] + nums[i] ,即:第i-1房一定是不考虑的,找出 下标i-2(包括i-2)以内的房屋,最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。
如果不偷第i房间,那么dp[i] = dp[i - 1],即考 虑i-1房,(注意这里是考虑,并不是一定要偷i-1房,这是很多同学容易混淆的点)
然后dp[i]取最大值,即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
代码
func rob(nums []int) int {n := len(nums)dp := make([]int, n+1) // dp[i]表示偷到第i家能够偷得的最大金额dp[1] = nums[0]for i := 2; i <= n; i++ {dp[i] = max(dp[i-1], dp[i-2] + nums[i-1])}return dp[n]
}func max(a, b int) int {if a > b {return a}return b
}
213.打家劫舍II
213.打家劫舍II
思路
成环收尾不能相连,所以分两种情况,第一种去掉头,第二种去掉尾,然后分别计算dp即可,最后取最大值即可。
思路代码
func rob(nums []int) int {if len(nums)==1{return nums[0]}if len(nums)==2{return max(nums[0],nums[1])}dp1:=make([]int,len(nums)-1)dp2:=make([]int,len(nums)-1)dp1[0]=nums[0]dp1[1]=max(nums[0],nums[1])dp2[0]=nums[1]dp2[1]=max(nums[1],nums[2])for i:=2;i<len(nums)-1;i++{dp1[i]=max(nums[i]+dp1[i-2],dp1[i-1])dp2[i]=max(nums[i+1]+dp2[i-2],dp2[i-1])}return max(dp1[len(nums)-2],dp2[len(nums)-2])
}func max(i,j int)int{if i<j{return j}return i
}
官方代码
func rob(nums []int) int {if len(nums) == 1 {return nums[0]}if len(nums) == 2 {return max(nums[0], nums[1])}result1 := robRange(nums, 0)result2 := robRange(nums, 1)return max(result1, result2)
}// 偷盗指定的范围
func robRange(nums []int, start int) int {dp := make([]int, len(nums))dp[1] = nums[start]for i := 2; i < len(nums); i++ {dp[i] = max(dp[i - 2] + nums[i - 1 + start], dp[i - 1])}return dp[len(nums) - 1]
}func max(a, b int) int {if a > b {return a}return b
}
困难
去掉头和去掉尾
337.打家劫舍III
思路
后序遍历
树形dp,返回当前偷还是不偷的情况
思路代码
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/
func rob(root *TreeNode) int {return max(dfs(root)[0],dfs(root)[1])
}func dfs(node *TreeNode) []int{if node==nil{return []int{0,0}}left:=dfs(node.Left)right:=dfs(node.Right)robthis:=node.Val+left[1]+right[1]notrobthis:=max(left[0],left[1])+max(right[0],right[1])return []int{robthis,notrobthis}
}func max(i,j int)int{if i<j{return j}return i
}
官方题解
这道题目算是树形dp的入门题目,因为是在树上进行状态转移,我们在讲解二叉树的时候说过递归三部曲,那么下面我以递归三部曲为框架,其中融合动规五部曲的内容来进行讲解。
确定递归函数的参数和返回值
这里我们要求一个节点 偷与不偷的两个状态所得到的金钱,那么返回值就是一个长度为2的数组。
参数为当前节点,代码如下:
vector robTree(TreeNode* cur) {
其实这里的返回数组就是dp数组。
所以dp数组(dp table)以及下标的含义:下标为0记录不偷该节点所得到的的最大金钱,下标为1记录偷该节点所得到的的最大金钱。
所以本题dp数组就是一个长度为2的数组!
那么有同学可能疑惑,长度为2的数组怎么标记树中每个节点的状态呢?
别忘了在递归的过程中,系统栈会保存每一层递归的参数。
如果还不理解的话,就接着往下看,看到代码就理解了哈。
代码
func rob(root *TreeNode) int {res := robTree(root)return max(res[0], res[1])
}func max(a, b int) int {if a > b {return a}return b
}func robTree(cur *TreeNode) []int {if cur == nil {return []int{0, 0}}// 后序遍历left := robTree(cur.Left)right := robTree(cur.Right)// 考虑去偷当前的屋子robCur := cur.Val + left[0] + right[0]// 考虑不去偷当前的屋子notRobCur := max(left[0], left[1]) + max(right[0], right[1])// 注意顺序:0:不偷,1:去偷return []int{notRobCur, robCur}
}
困难
树形dp,长度只需为2,别忘了在递归的过程中,系统栈会保存每一层递归的参数。
今日收获
打家劫舍问题,重点是当前位置偷还是不偷,然后判断哪种更大。
树形dp,长度只需为2,别忘了在递归的过程中,系统栈会保存每一层递归的参数。
这道题是树形DP的入门题目,通过这道题目大家应该也了解了,所谓树形DP就是在树上进行递归公式的推导。
所以树形DP也没有那么神秘!
只不过平时我们习惯了在一维数组或者二维数组上推导公式,一下子换成了树,就需要对树的遍历方式足够了解!
相关文章:

动态规划part9 | ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III
文章目录 198.打家劫舍思路思路代码官方题解代码 213.打家劫舍II思路思路代码官方代码困难 337.打家劫舍III思路思路代码官方题解代码困难 今日收获 198.打家劫舍 198.打家劫舍 思路 dp含义,偷前i个房,切第i个房偷 dp[i]max(dp[i-2],dp[i-3])nums[i] …...
【k8s系列】一分钟搭建MicroK8s Dashboard
本文基于上一篇文章的内容进行Dashboard搭建,如果没有看过上一篇的同学请先查阅上一篇文章 k8s系列】使用MicroK8s 5分钟搭建k8s集群含踩坑经验 使用MicroK8s搭建Dashboard很简单,只需要在Master节点按照以下几步操作 1.启用Dashboard插件 microk8s en…...
ArcEngine二次开发0——入门(下载 部署 组件学习)
折腾一下ArcGIS Engine二次开发。 目录 1、开发环境配置2、部署一个ArcGIS Engine应用程序3、ArcObject组件学习4、报错及解决4、其他 1、开发环境配置 参考:https://blog.csdn.net/H48662654/article/details/113384150 (使用ArcEngine前,…...
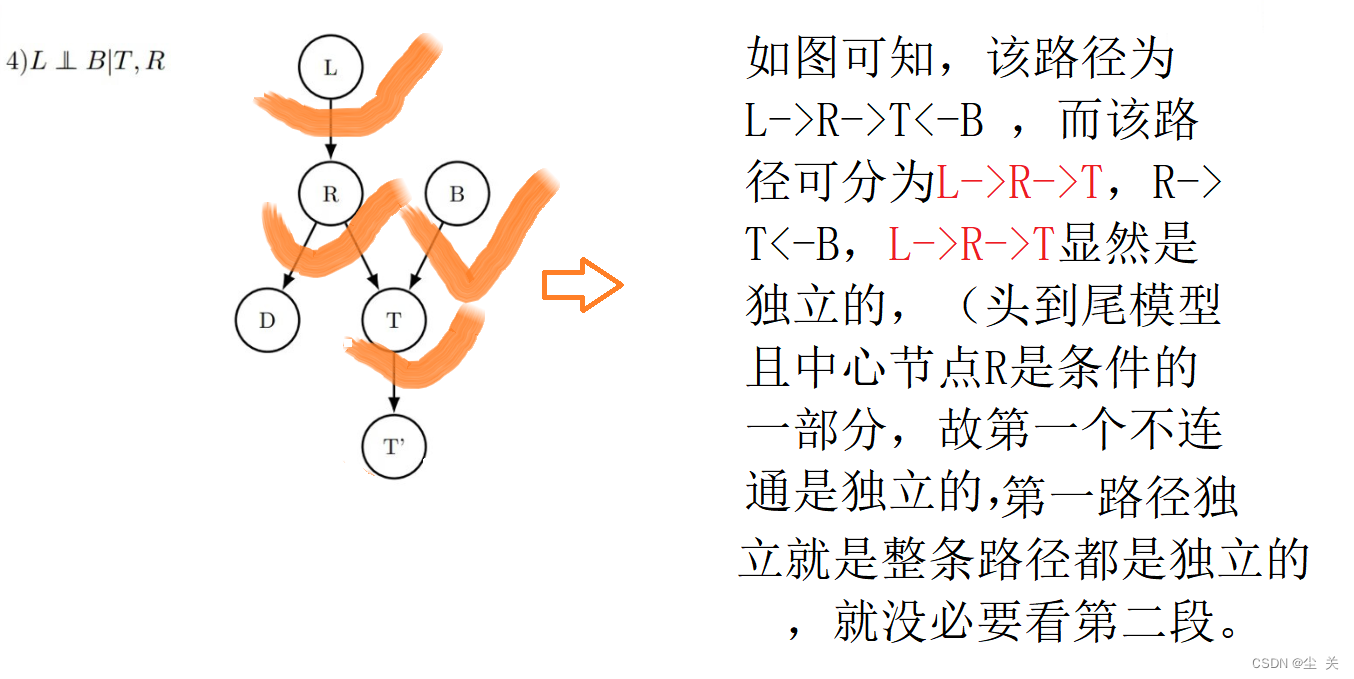
人工智能---D分离
D分离(D-Separation)是一种用来判断变量是否条件独立的图形化方法。相比于非图形化方法,D-Separation更加直观,且计算简单。对于一个DAG(有向无环图)E,D-Separation方法可以快速的判断出两个节点…...
java spring cloud 企业工程项目管理系统源码-全面的工程项目管理
工程项目管理系统是指从事工程项目管理的企业(以下简称工程项目管理企业)受业主委托,按照合同约定,代表业主对工程项目的组织实施进行全过程或若干阶段的管理和服务。 如今建筑行业竞争激烈,内卷严重,…...

2023最新软件测试面试题【1000道题含答案】
1、自动化代码中,用到了哪些设计模式? 单例设计模式 工厂模式PO设计模式数据驱动模式面向接口编程设计模式 2、什么是断言( Assert) ? 断言Assert用于在代码中验证实际结果是不是符合预期结果,如果测试用例执行失败会抛出异常并提供断言日志 3、什么是web自动化测…...

【目标跟踪】MOT数据集GroundTruth可视化
MOT数据集格式简介 MOT15数据集下载:https://pan.baidu.com/s/1foGrBXvsanW8BI4eybqfWg?pwd8888 以下为一行gt示例: 1,1,1367,393,73,225,1,-1,-1,-1 各列数据对应含义如下 <frame>,<id>,<bb_left>,<bb_top>,<bb_width&g…...

软件测试的概念与过程----学习软件测试前的思考
软件测试的概念与过程----学习软件测试前的思考 1、软件测试工作是做什么的?2、那我做软件测试拿到一个软件产品我应该从哪里测试,怎末开始工作?3、测试早做好还是晚一些做好?4、软件测试能将软件测试的一点问题都没有嘛ÿ…...

Streamlit基础教程
streamlit是什么 streamlit是一个开源的python库,它能够快速的帮助我们创建定制化的web应用,而且还非常便于和他人分享,特别是在机器学习和数据科学领域。整个过程不需要你了解任何前端的知识,包括html、css、javascript等&#x…...

内网穿透技术
文章目录 前言1. 安装JAVA2. MCSManager安装3.局域网访问MCSM4.创建我的世界服务器5.局域网联机测试6.安装cpolar内网穿透7. 配置公网访问地址8.远程联机测试9. 配置固定远程联机端口地址9.1 保留一个固定tcp地址9.2 配置固定公网TCP地址9.3 使用固定公网地址远程联机 转载自内…...

计算机网络笔记:内部网关协议RIP
文章目录 1.协议RIP的工作原理2.距离向量算法3.坏消息传播得慢 1.协议RIP的工作原理 RIP的地位:RIP是内部网关协议IGP中最先得到广泛使用的协议,其中文译名为路由信息协议。 RIP概述: RIP是一种分布式的基于距离向量的路由选择协议&#x…...
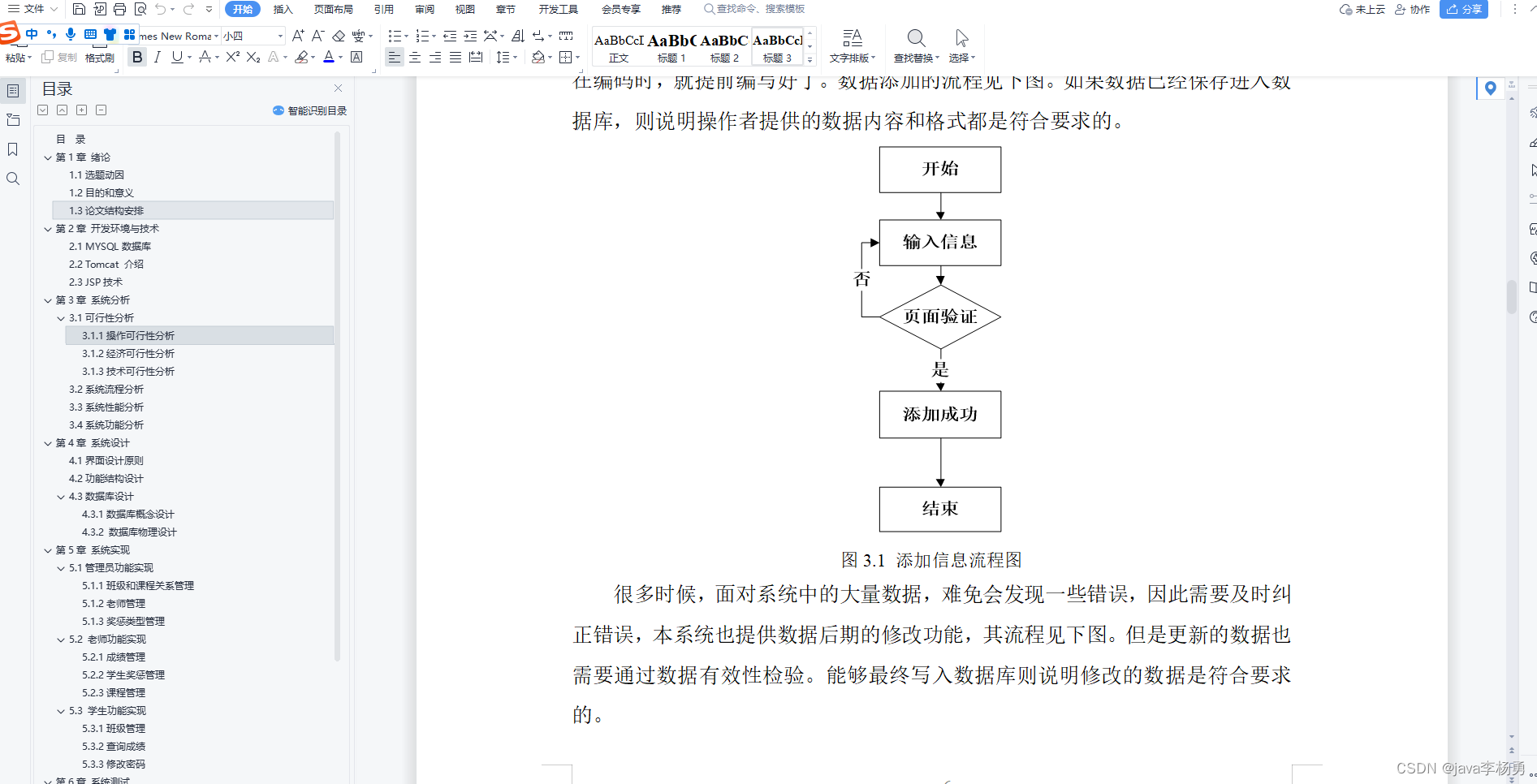
基于Java学生信息管理系统设计实现(源码+lw+部署文档+讲解等)
博主介绍: ✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战 ✌ 🍅 文末获取源码联系 🍅 👇🏻 精…...

PHP简单入门
PHP是一种流行的服务器端编程语言,被广泛用于Web开发。许多著名的网站和应用程序都是使用PHP编写的,例如Facebook、Wikipedia和WordPress等。本篇文章将为您介绍如何入门PHP编程。 环境配置 在开始使用PHP之前,需要先配置开发环境。要在本…...

java 客户端操作HDFS
1、windows上部署hadoop包 部署包win版本 源码包zip包 lib整合:共121个jar包 $HADOOP_PREFIX/share/hadoop/{common,hdfs,mapreduce,yarn,tools}/{lib,.}*.jar 将windows版本hadoop/bin/hadoop.dll 放到c:/windows/system32下 2、windows环境变量配置 hadoop的…...

区块链中的共识机制以及共识算法
目录 什么是共识 什么是共识机制 共识机制类型 1、基于工作证明(Proof of Work PoW)...

【计算机网络自顶向下】DNS简答题总结
主要功能:将域名解析为主机能识别的IP地址 DNS实现的功能 主机到IP地址的转换主机别名的转换邮件服务器别名负载均衡 DNS实现冗余服务器:一个IP地址集合对应同一个规范主机名 域名系统 分布式数据库:一个由多层DNS服务器实现的分布式数据库应…...

【QQ界面展示-实现自动回复 Objective-C语言】
一、刚才咱们监听键盘弹出事件,是怎么监听的, 1.监听键盘弹出事件的步骤 1)首先,在控制器的viewDidLoad方法中,创建一个NotificationCenter对象啊 2)通过center,让当前控制器的这个方法,监听这个通知, 3)然后,我们在这个通知里面,获取到键盘的Y值, 4)对我们的…...

-bash: ssh: command not found
解决方法: 命令安装SSH: yum -y install openssh-clients [roothad2 ~]# yum -y install openssh-clients Loaded plugins: fastestmirror Loading mirror speeds from cached hostfile * base: mirrors.qlu.edu.cn * extras: mirrors.ustc.edu.cn …...
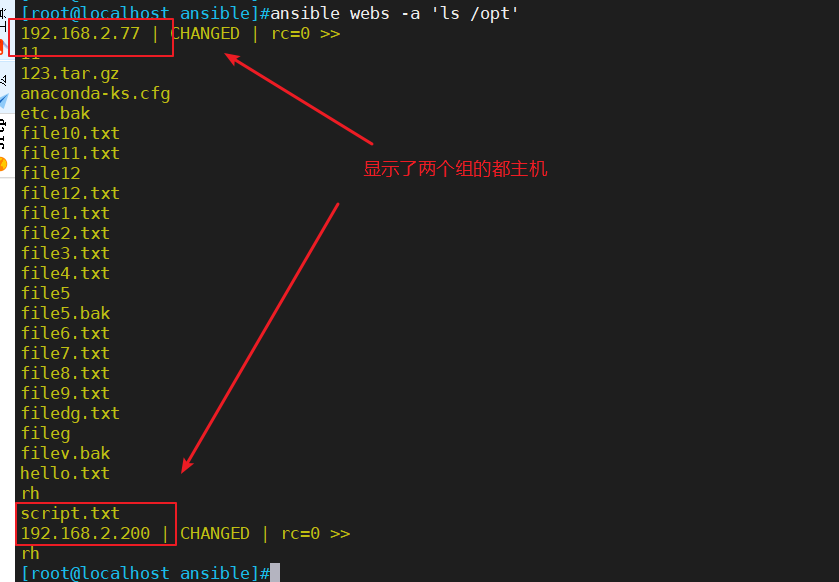
ansible的部署和模块
一、 ansible 的概述 1、ansible简介 Ansible是一款为类Unix系统开发的自由开源的配置和自动化工具。 它用Python写成,类似于saltstack和Puppet,但是有一个不同和优点是我们不需要在节点中安装任何客户端。 它使用SSH来和节点进行通信。Ansible基于 …...
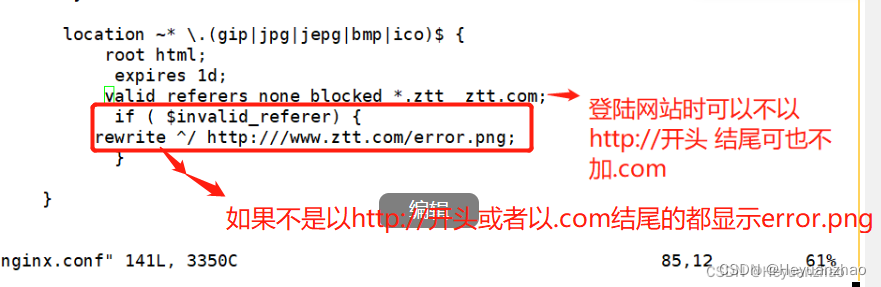
nginx的优化
目录 一 隐藏版本号在网页上面有nginx的版本号会让别人攻击你的服务器 二 nginx的优化之日志分割 三 nginx的优化之页面压缩 四 连接超时 五 nginx的并发设置 七总结:nginx的优化 一 隐藏版本号在网页上面有nginx的版本号会让别人攻击你的服务器 如图所示 第一种方法是关…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...
