13-C++算法笔记-递归
📚 Introduction
递归是一种常用的算法设计和问题求解方法。它基于问题可以分解为相同类型的子问题,并通过解决子问题来解决原始问题的思想。递归算法在实际编程中具有广泛的应用。
🎯 递归算法解决问题的特点
递归算法具有以下特点:
- 问题可以分解为相同类型的子问题。
- 递归算法通过解决子问题来解决原始问题。
- 递归算法在解决问题时使用自己调用自己的方式。
📝 递推算法练习题
🐰 1. 斐波那契数列
题目描述:
斐波那契数列是指这样的数列:数列的第一个和第二个数都为1,接下来每个数都等于前面两个数之和。现在给定一个正整数n,要求计算斐波那契数列的第n个数。
💡 思路解析:
- 基本情况: 当n为1或2时,直接返回1。
- 递归过程: 对于其他n,递归计算斐波那契数列的第n-1和n-2个数,并将它们相加。
#include <iostream>
using namespace std;int fibonacci(int n) {if (n <= 2) {return 1;}return fibonacci(n - 1) + fibonacci(n - 2);
}int main() {int n = 6;cout << "斐波那契数列的第" << n << "个数为:" << fibonacci(n) << endl;return 0;
}
解题步骤图:
🔄 2. 阶乘计算
题目描述:
阶乘是指从1乘积到给定的正整数n。现在给定一个正整数n,要求计算n的阶乘。
💡 思路解析:
- 基本情况: 当n为0或1时,直接返回1。
- 递归过程: 对于其他n,递归计算n-1的阶乘,并将其乘以n。
#include <iostream>
using namespace std;int factorial(int n) {if (n <= 1) {return 1;}return n * factorial(n - 1);
}int main() {int n = 5;cout << n << "的阶乘为:" << factorial(n) << endl;return 0;
}
解题步骤图:
📏 3. 最大公约数
题目描述:
给定两个正整数a和b,要求计算它们的最大公约数。
💡 思路解析:
- 基本情况: 当b等于0时,直接返回a。
- 递归过程: 对于其他情况,递归计算b和a除以b的余数的最大公约数。
#include <iostream>
using namespace std;int gcd(int a, int b) {if (b == 0) {return a;}return gcd(b, a % b);
}int main() {int a = 24;int b = 36;cout << a << "和" << b << "的最大公约数为:" << gcd(a, b) << endl;return 0;
}
解题步骤图:
以上代码分别使用递归算法解决了斐波那契数列、阶乘计算和最大公约数的问题。通过递归的方式,我们可以简洁地解决这些问题,并且代码具有可读性和可维护性。
📚 总结
递归算法是一种强大的问题求解方法,通过将问题分解为相同类型的子问题,可以高效地解决各种复杂的问题。在编写递归算法时,需要注意定义好基本情况和递归的终止条件,确保算法的正确性和有效性。通过递归算法的练习,我们可以更深入地理解递归思想和算法设计的精妙之处。
⭐️希望本篇文章对你有所帮助。
⭐️如果你有任何问题或疑惑,请随时向提问。
⭐️感谢阅读!
相关文章:

13-C++算法笔记-递归
📚 Introduction 递归是一种常用的算法设计和问题求解方法。它基于问题可以分解为相同类型的子问题,并通过解决子问题来解决原始问题的思想。递归算法在实际编程中具有广泛的应用。 🎯 递归算法解决问题的特点 递归算法具有以下特点&#…...
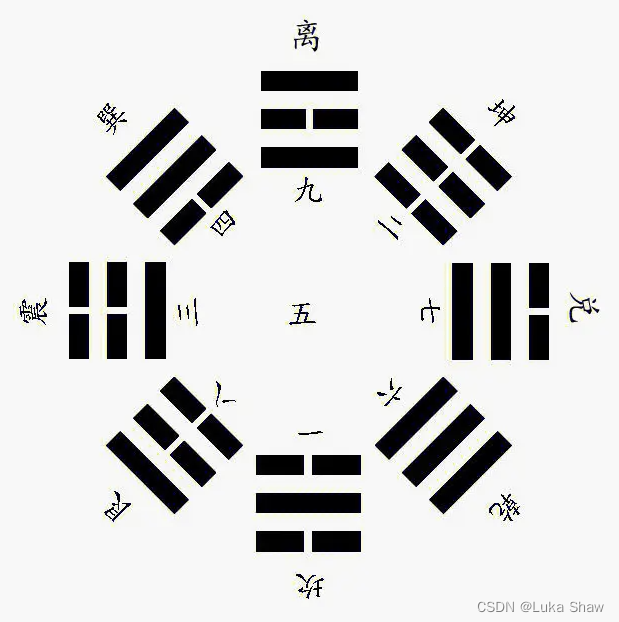
从古代八卦探究计算机的八进制
八进制,即八卦,是中国古代哲学体系中非常重要的一个概念,它被广泛应用于易经、道家、儒家等诸多领域。随着计算机科学的快速发展,人们开始思考:八进制是否可以应用到计算机上? 一、什么是八进制࿱…...

Linux shell mkfs.ext4命令参数使用
mkfs mkfs是个综合命令 mkfs 然后按两下tab 查看系统支持哪些文件系统的格式化功能 mkfs -t 文件系统格式名 以指定的文件系统格式来进行磁盘格式化 > 等于 mkfs.文件系统格式名 比如: mkfs -t xfs mkfs.xfs 常见的磁盘格式…...

【Docker】子系统与其相关名词的界定、Control Groups等详细讲解
前言 Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的容器中,然后发布到任何流行的Linux或Windows操作系统的机器上,也可以实现虚拟化,容器是完全使用沙箱机制,相互之间不会有任何接口。 📕作者简介:热…...

spring事务的传播性与隔离性
spring事务的传播性 REQUIRED(必须的)(TransactionDefinition.PROPAGATION_REQUIRED) 使用当前的事务,如果当前没有事务,则自己新建一个事务,子方法是必须运行在一个事务中的,如果当前存在事务,…...
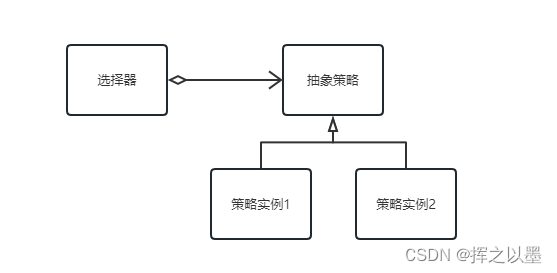
【设计模式】模板方法与策略模式的结合使用
文章目录 1. 概述1.1.简述模板方法 2.模板方法实现2.1.简单实现2.2.在SpringBoot中的实现 3.模板方法与策略模式的结合使用3.1.代码实现 4.总结 1. 概述 模板方法是一种非常简单的设计模式,只要能够理解面向对象中的继承与多态就能够理解这种设计模式,我…...
Jmeter实现参数加密
目录 一、使用__digest自带函数 以md5加密算法演示使用方法 二、在BeanShell 中使用JAVA代码实现算法加密 规避BUG的方法 JMeter有两种方法可以实现算法加密 一、使用__digest自带函数 参数说明: Digest algorithm:算法摘要,可输入值&a…...
)
Solon Web 开发:四、认识请求上下文(Context)
Handler Context 架构,是Solon Web 的基础。在 Context (org.noear.solon.core.handle.Context)里可以获取: 请求相关的对象与接口会话状态相关的对象与接口响应相关的对象与接口 或者理解所有请求与响应相关的,都在…...
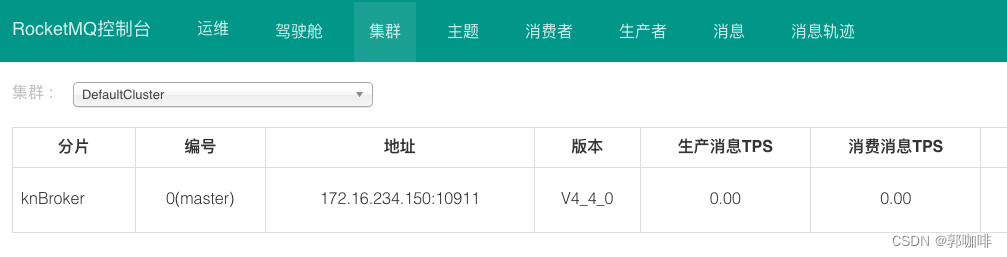
docker安装RocketMQ(附填坑经验connect to <172.17.0.3:10909> failed)
目录 一、docker部署RocketMQ1、简易说明2、docker拉取RocketMQ镜像\RocketMQ控制台3、获取RocketMQ配置文件4、RocketMQ配置文件描述5、docker启动RocketMQ6、进入RocketMQ控制台 二、填坑经验错误一: connect to <172.17.0.3:10909> failed错误二: maybe your broker m…...
GRU、LSTM、注意力机制(第八次组会)
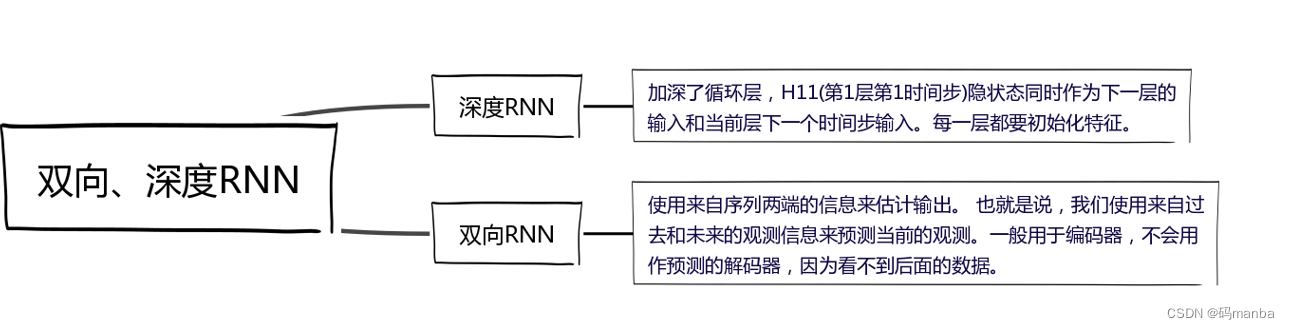
GRU、LSTM、注意力机制(第八次组会) 一、 GRU二、 LSTM三、 深度RNN、双向RNN四、 注意力机制一、 GRU 二、 LSTM 三、 深度RNN、双向RNN...
@RequestBody、@RequestParam和@PathVariable三个注解的区别和使用)
问题杂谈(三十六)@RequestBody、@RequestParam和@PathVariable三个注解的区别和使用
总结: 在后端的同一个接收方法里,RequestBody与RequestParam()可以同时使用RequestBody最多只能有一个,而RequestParam()可以有多个RequestBody 接收的是请求体里面的数据,所以一般用POST请求;而RequestParam接收的是…...

Flutter学习四:Flutter开发基础(六)调试Flutter应用
目录 0 引言 1 调试Flutter应用 1.1 日志与断点 1.1.1 debugger() 声明 1.1.2 print和debugPrint 1.1.3 调试模式、中间模式、发布模式 1.1.4 断点 1.2 调试应用程序层 1.2.1 转储Widgets树 1.2.2 转储渲染树 1.2.3 转储Layer树 1.2.4 转储语义树 1.2.5 调度&…...
)
新的开始(开始更新笔记)
首先感谢关注我的小伙伴,以后在求职或者选择方向的时候,感觉迷茫的时候,可以加我聊聊。 一路走来,跌跌撞撞,磕磕碰碰,经历了很多,记得上一次的更新笔记还是2021年。 首先说一下我的经历&#…...

爬虫工具-替换js文件ReRes插件/Gores插件
目录 一、ReRes插件二、Gores插件 一、ReRes插件 用途:爬虫逆向过程中一些文件需要替换时 ① 原始网站js文件有无限debugger,复制原始网站js文件,删掉无限debugger相关代码保存为新的js文件;用ReRes插件进行替换② 原始网站js文件…...

多任务学习用于多模态生物数据分析
目前的生物技术可以同时测量来自同一细胞的多种模态数据(例如RNA、DNA可及性和蛋白质)。这需要结合不同的分析任务(如多模态整合和跨模态分析)来全面理解这些数据,推断基因调控如何驱动生物多样性。然而,目…...

使用less命令搜索文件中的关键字
目录 介绍常用搜索技巧实例 介绍 less 与 more 类似,less 可以随意浏览文件,支持翻页和搜索,支持向上翻页和向下翻页。 语法 less [参数] 文件 参数说明: -b <缓冲区大小> 设置缓冲区的大小 -e 当文件显示结束后ÿ…...

【kubernetes系列】Kubernetes之Taints和tolerations
概述 节点亲和性是pod的一种属性(优先选择或硬性要求),它使 pod 被优先分配到一类特定的节点上。而Taint则相反,它使节点能够排斥一类特定的 pod。 Taints(污点)与tolerations(容忍度…...
)
宝剑锋从磨砺出 梅花香自苦寒来(高考志愿篇)
各省高考成绩已出,又到一年高考季。张雪峰提到:“普通家庭不要光谈理想,也要谈落地。”志愿怎样填报、选专业还是选学校、什么专业好就业、高考志愿主要看什么?针对这些疑问,你对正在选志愿的毕业生们有什么建议吗&…...

Jtti:怎样进行sql server2000 日志传送
在 SQL Server 2000 中,日志传送是指将事务日志从一个主服务器传送到一个或多个备份服务器的过程。这个过程确保备份服务器上的数据库保持与主服务器上的数据库同步。 要进行 SQL Server 2000 的日志传送,需要进行以下步骤: 配置主服务器&…...

MyBatis-Plus:条件构造器Wrapper
目录 1.Wrapper概述 1.1.Wrapper的继承关系 1.2.Wapper介绍 1.3.各个构造器使用区别 1.4.构造器常用方法 2.Wrapper常用构造器介绍 2.1.QueryWrapper 2.2.UpdateWrapper 2.3.LambdaQueryWrapper 2.4.AbstractWrapper 3. Lambda条件构造器 3.1.示例 4.鸣谢 MyBati…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...
