贝叶斯与认知——读《贝叶斯的博弈》有感
关于对贝叶斯与认知问题的相关思考
- 一、贝叶斯定理
- 二、贝叶斯与认知的本质
- 三、经验的偏见
- 四、总结
自古以来,人们就在思考知识来自何处,“冯翼惟象,何以识之?”,对此的思考逐渐发展成哲学的认识论分支。德国哲学家康德指出,“所有人类知识从直觉开始,然后转变为观念,最后化为思想”。法国数学家拉普拉斯进一步阐释到,“概率论本质不过是化为计算的常识,它以准确的方式评价那些政策的头脑通过某种直觉领会到的东西,而这种直接领会经常不被察觉”。
人类认识研究自然、开展社会实践,包括现在的人工智能都遵循着,做出假设、收集数据、判断决策、观察结果、修正假设的周而复始的类似过程。
贝叶斯公式通过简洁的数学形式,将人类的基本感知与高级推理相结合,定义了人类对世界的认知过程。根据贝叶斯公式,我们不断获取有效的知识,英国靠它破译二战德军密码,医疗业靠它辅助诊断,银行业靠它发放贷款,互联网靠它推荐商品,而人工智能更是靠它实现了飞跃。
一、贝叶斯定理
1763年12月23日,托马斯·贝叶斯的遗产受赠者R. Price牧师在英国皇家学会宣读了贝叶斯的遗作《An essay towards solving a problem in the doctrine of chances》(《论机会学说中一个问题的求解》),其中给出了贝叶斯定理。贝叶斯定理是一种统计学方法,其基本工具就是贝叶斯公式: P ( A ∣ B ) = P ( A ) P ( B ∣ A ) / P ( B ) P(A|B)=P(A)P(B|A)/P(B) P(A∣B)=P(A)P(B∣A)/P(B)其中, P ( A ) P(A) P(A)为事件 A A A的先验概率, P ( A ∣ B ) P(A|B) P(A∣B)为事件 B B B条件下,事件A的后验概率; P ( B ) P(B) P(B)为事件 B B B的先验概率, P ( B ∣ A ) P(B|A) P(B∣A) 为事件 A A A条件下,事件 B B B的后验概率。

贝叶斯定理广泛应用于各个领域的推断、决策中。以医疗诊断为例,假设肺癌发病率 P ( A ) = 0.001 P(A)=0.001 P(A)=0.001,吸烟人群占比 P ( B ) = 0.4 P(B)=0.4 P(B)=0.4,而肺癌病人中有 80 % 80\% 80%吸烟 ,即 P ( B ∣ A ) = 0.8 P(B|A)= 0.8 P(B∣A)=0.8,则若某患者吸烟,则该患者肺癌的概率: P ( A ∣ B ) = P ( A ) P ( B ∣ A ) / P ( B ) = 0.001 ∗ 0.8 / 0.4 = 0.002 P(A|B)=P(A) P(B|A)/P(B)=0.001*0.8/0.4 =0.002 P(A∣B)=P(A)P(B∣A)/P(B)=0.001∗0.8/0.4=0.002该例中,贝叶斯公式将先验概率 P ( A ) P(A) P(A)转化为了后验概率 P ( A ∣ B ) P(A|B) P(A∣B),这个过程中主要利用了观察数据 P ( B ∣ A ) P(B|A) P(B∣A) 。肺癌发病率只有 P ( A ) = 0.001 P(A)=0.001 P(A)=0.001,但是根据观察数据发现,肺癌病人的吸烟者比率 P ( B ∣ A ) = 0.8 P(B|A)= 0.8 P(B∣A)=0.8高于整体人群的吸烟者占比 P ( B ) = 0.4 P(B)=0.4 P(B)=0.4,因此增强了吸烟者中肺癌发病率的信念。
二、贝叶斯与认知的本质
贝叶斯定理之所以得到广泛应用,核心在于其本质符合人类认识的普遍规律与日常解决问题的通用方式,即“我”对客观世界总有一个主观的先验判断,但这个判断会随着“我”对真实世界的观察而修正,从而对世界永远保持开放的态度。其中,贝叶斯公式中的先验概率代表初始的主观判断,实质上也是经验统计的结果(先验信息一般来自历史经验与资料、甚至直觉),而后验概率代表对当前真实世界的观测(一般来自于当前的实践过程、观测数据)。
贝叶斯定理从“观察者”角度(即“人”的角度)出发,认为概率是主观对某个事物发生的相信程度,由于“观察者”知识的不完备,需要不断从对客观世界的观察中得到规律更新对事件的假设。
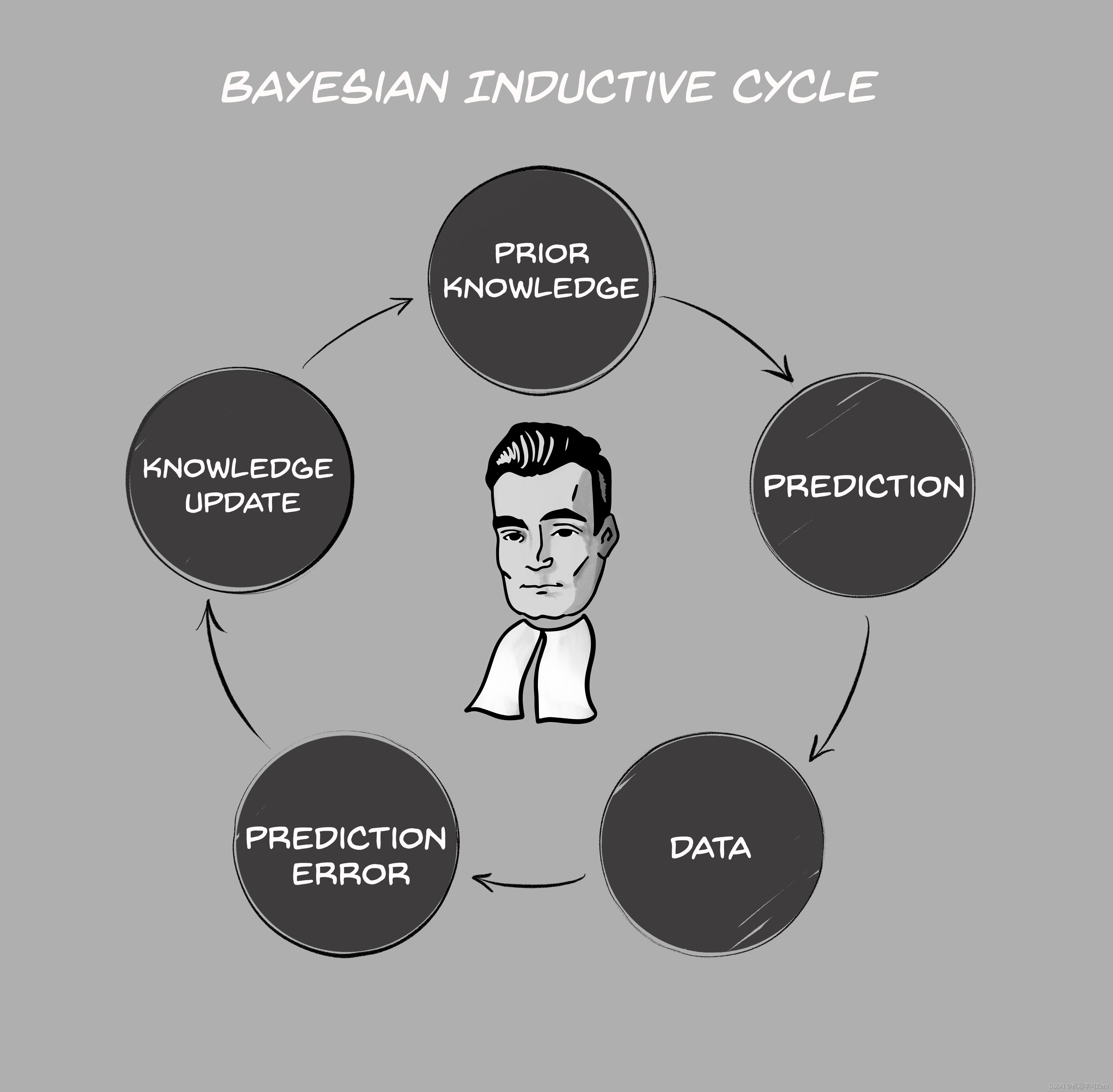
从这点来说,贝叶斯定理与马克思主义哲学的基本观点也是一致的。马克思主义哲学认为,人的认识都是一步步由低级向高级发展,即由浅入深,由片面到更多的方面。认识的过程分为感性阶段与理性阶段,感性阶段是开始接触外界事情,属于感觉的阶段;理性阶段是综合感觉的材料加以整理和改造,属于概念、判断和推理的阶段。理性认识依赖于感性认识,感性认识有待于发展到理性认识,这是辩证唯物论的认识论。

同时马克思主义深刻指出,只有人的社会实践,才是人们对于外界认识的真理性的标准。实践就是不断的观察世界,获取新的数据的过程,而发展真理则是不断对主观判断的修正。在实践过程中,人们达到预期结果时,认识才被证实。要想得到预期结果,一定要使自己的认知符合客观规律,否则就会在实践中失败。而经过失败后,从失败取得教训,改正自己的认识使之符合客观规,就能变失败为胜利,所谓“失败者成功之母”,“吃一堑长一智”。
三、经验的偏见
贝叶斯定理中“观察者”基于经验会对事件有个初始判断,而基于经验的判断往往存在不同程度的偏差。
《贝叶斯的博弈》一书中引用了阿莫斯·特沃斯基和丹尼尔·卡内曼两位心理学研究者提出的“琳达问题”:琳达31岁,独身,为人诚恳且充满智慧。她学习过哲学。她在还是大学生的时候就很关心歧视与社会正义的问题,也曾参加反核游行。下面哪个陈述更有可能正确:A.琳达是银行办事员。B.琳达是银行办事员,并且活跃在女权运动中。在该问题的多次实验中,85%以上的测试者选择了错误答案B。实际上,B是A的特殊情况,即B是A的子集,从概率上来说 P ( B ) ≤ ( A ) P(B)≤(A) P(B)≤(A),因此A是正确答案。特沃斯基和卡内曼认为,针对此类问题,人们更多是进行关联性的推理,而非数学推理,对于31岁、独身、接受过高等教育、参加过反歧视运动的女性的此类特征,选项B更令人信服。

尼曼和特沃斯基还发现,在回答“A物体是否属于S类”这种问题时,由于经验的偏见,人们容易出现代表性偏差。比如A是个害羞的人,他更可能是围棋选手还是销售员?大多数人会感觉A肯定更应该是围棋选手,因为害羞像围棋选手的代表性特征,而对销售员来说,这个特点太过异常。
然而,属于某一类的可能性还要受其他许多重要因素的影响。该例子中,A是围棋选手还是销售员还的可能性大,主要是受这两种职业在总人口中所占相对比例的影响。假设总人口中销售员所占比是20%,围棋选手则是0.1%,而10%的销售员害羞,而围棋选手害羞的有90%。则每1000人,害羞的销售员是20人,而害羞的围棋选手只有0.9人,因此此类情况下,一个害羞的人更可能是一个围棋选手。
通过上述例子,可以看出仅靠经验或理论做出的判断往往会造成偏见。《贝叶斯的博弈》中写到,“我们都是本能上不能理性的笨蛋,无法正确修订我们的信念,而理解贝叶斯的这个法则真的可以帮助改善我们自身”。

因此,要解决问题就不能仅靠理论或经验,要充分调查研究,结合客观实际具体问题具体分析。“没有调查,就没有发言权”,调查研究的过程就是对当前情况充分观测、获取数据的过程,从而将理论与客观实际相结合,看它是否在实践中能够达到预期。

许多科学理论之所以被称为真理,不在于科学家们创立这些学说的时候,而且在于为尔后的科学实践所证实的时候。人类认识的历史告诉我们,许多理论的真理性是不完全的,经过实践的检验而纠正了它们的不完全性。许多理论是错误的,经过实践的检验而纠正其错误。实践是检验真理的唯一标准,所谓“生活、实践底观点,应该是认识论底首先的和基本的观点”。
四、总结
“根据贝叶斯定理,任何理论都不完美。取而代之的是一项未尽的工作,它永远处于推敲与测试之中。”贝叶斯状态就是一种平衡于确信与怀疑之间的状态,在这种状态下,人们不会轻易相信谣言,也可以勇敢挑战权威。

正像毛泽东同志《实践论》指出的那样,“通过实践而发现真理,又通过实践而证实真理和发展真理。从感性认识而能动地发展到理性认识,又从理性认识而能动地指导革命实践,改造主观世界和客观世界”。实践、认识、再实践、再认识,这种形式,循环往复以至无穷,而实践和认识之每一循环的内容,都比较地进到了高一级的程度,这就是辩证唯物论的全部认识论,也就是所谓“知行合一”。
相关文章:

贝叶斯与认知——读《贝叶斯的博弈》有感
关于对贝叶斯与认知问题的相关思考 一、贝叶斯定理二、贝叶斯与认知的本质三、经验的偏见四、总结 自古以来,人们就在思考知识来自何处,“冯翼惟象,何以识之?”,对此的思考逐渐发展成哲学的认识论分支。德国哲学家康德…...
MySQL安装失败starting the sever
MySQL安装失败starting the sever 如果电脑是第一次安装MySQL,一般不会出现这样的报错。starting the sever失败,通常是因为上次安装该软件没有清除干净。 第一种解决方法:完全卸载mysql,重新安装 完全卸载该软件的办法&#…...

合并文件夹中所有文件,并输出重复的条形码值
文章目录 一、需求二、处理方式三、代码实现 一、需求 每天会生成一个记录文件(文件名按日期yyyyMMdd格式命名),记录文件中记录有条形码的内容,需要合并最近20次的数据,并提取出有重复的条形码。 也可以进行最近30天数…...

P3089 [USACO13NOV] Pogo-Cow S 弹簧踩高跷
P3089 [USACO13NOV] Pogo-Cow S 弹簧踩高跷 洛谷题目传送门 文章目录 P3089 [USACO13NOV] Pogo-Cow S 弹簧踩高跷题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示题目大意方法一(线段树维护dp)code 方法二 (单调队列维护dp&…...
计算机网络 - 第一章(下)
1.2_1 分层结构、协议、接口、服务_哔哩哔哩_bilibili1.2_1 分层结构、协议、接口、服务是王道计算机考研 计算机网络的第7集视频,该合集共计76集,视频收藏或关注UP主,及时了解更多相关视频内容。https://www.bilibili.com/video/BV19E411D78…...

【Uniapp】小程序携带Token请求接口+无感知登录方案2.0
本次改进原文《【Uniapp】小程序携带Token请求接口无感知登录方案》,在实际使用过程中我发现以下bug: 若token恰好在用户访问接口时到期,就会直接查询为空,不反映token过期问题(例如:弹窗显示订单查询记录…...
Ubuntu常用命令
文章目录 1:文件管理2:文档编辑3:系统管理4:磁盘管理5:文件传输6:网络通讯7:设备管理8:备份压缩9:其他命令扩展:知识干货 1:文件管理 ls命令 –…...
ERP重构-SLA子分类账-分布式实现方案
背景 ERP中的GL总账模块,明细数据来源于各个业务模块如库存、成本、应收、应付、费控、资产等,统称为子模块,生成的账叫做子分类账。然而记账的业务逻辑各式各样,但是最终输出都是来源、类型、期间、科目、借贷金额等等关键信息。…...

IP路由协议(RIP、IGRP、OSPF、IS-IS、BGP)
文章目录 1、路由分类2、RIP协议1)RIP的工作原理2)RIP路由表的更新过程3)RIP路由表的更新原则4)RIP的特性5)RIP协议的版本 4、IGRP协议1)IGRP路由表的更新2)IGRP的度量标准 5、OSPF协议1&#x…...
互斥锁、自旋锁、读写锁、悲观锁、乐观锁的应用场景
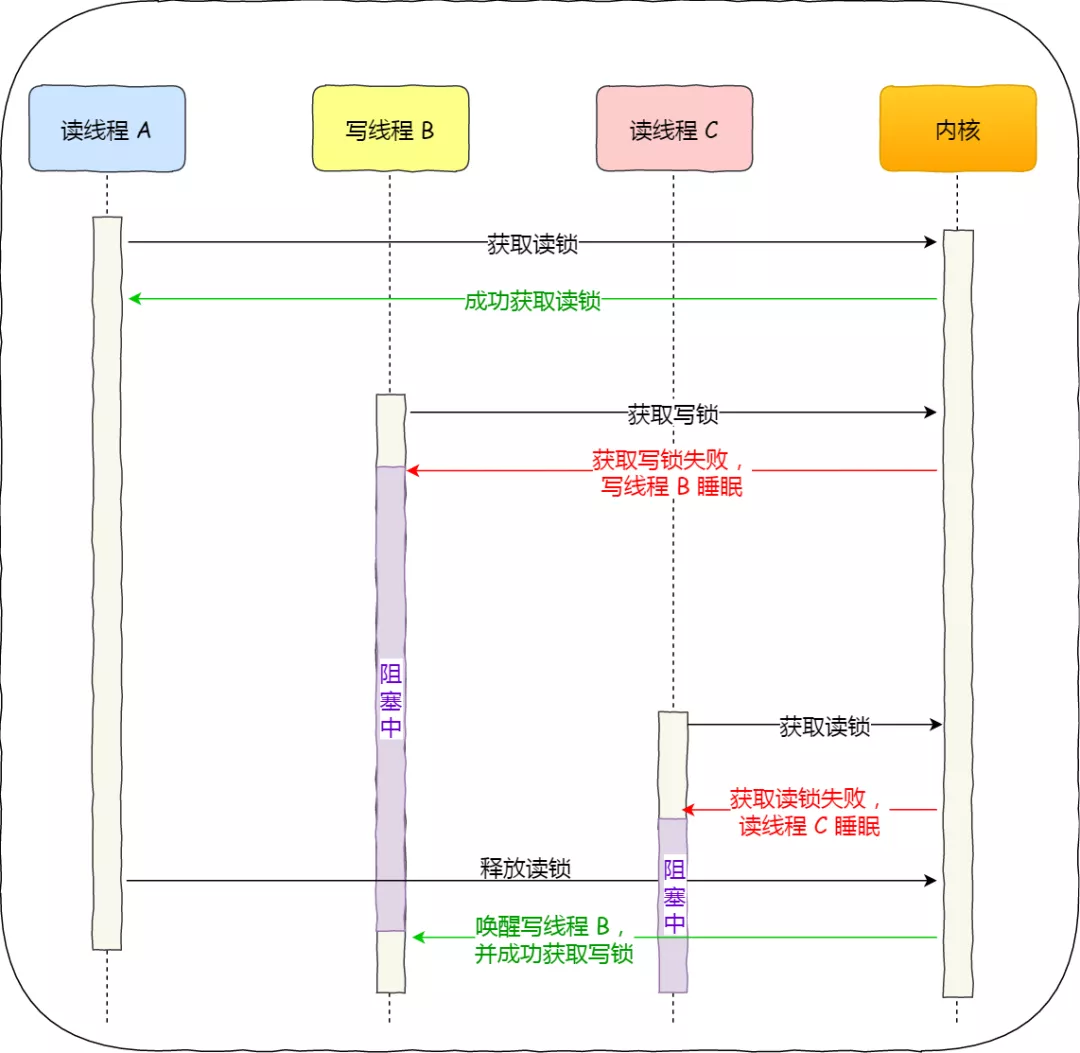
多线程访问共享资源的时候,避免不了资源竞争而导致数据错乱的问题,所以我们通常为了解决这一问题,都会在访问共享资源之前加锁。 最常用的就是互斥锁,当然还有很多种不同的锁,比如自旋锁、读写锁、乐观锁等࿰…...
Python WSGI 与 Web 开发框架
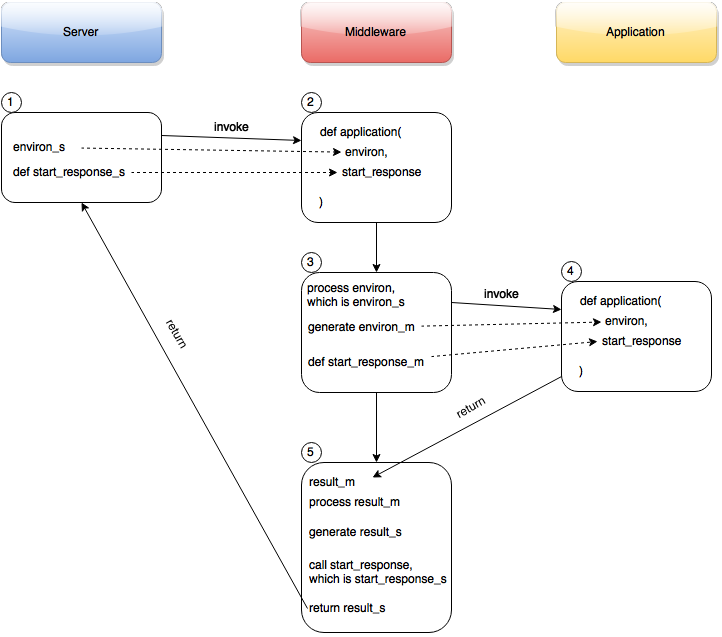
目录 文章目录 目录WSGIWSGI 的工作原理environ 参数start_resposne 参数 WSGI 的中间件 WSGI Web 开发框架OpenStack 中的应用案例进程入口WSGI Application 加载Paste/PasteDeployRoutesWebOb WSGI Server 启动 WSGI WSGI(Web Server Gateway Interfaceÿ…...

[洛谷]P6464 [传智杯 #2 决赛] 传送门
看到数据范围:n<100,嗯......脑子闪过:还在想什么呢!Floyd啊。哈哈哈 思路: 详细注释: 话不多说,上ACcode!: #include<bits/stdc.h> using namespace std; #define int lo…...

Http协议和RestTemplate协议有什么区别?
目录 一、功能不同 二、技术不同 三、使用场景不同 四、总结 RestTemplate 是一个 Spring 框架提供的用于发送 HTTP请求的客户端工具,它封装了 Java 原生的 HTTP 客户端库,并提供了一组简洁易用的 API 来发送 HTTP 请求和处理响应。而 HTTPÿ…...
基于SpringBoot+微信小程序的医院预约叫号小程序
✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍: 该项目是基于uniappWe…...

springboot整合RabbitMQ 消费端处理数据
pom 依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-amqp</artifactId></dependency>写一个rabbitmq配置文件 import org.springframework.amqp.core.Binding; import org.springframewo…...
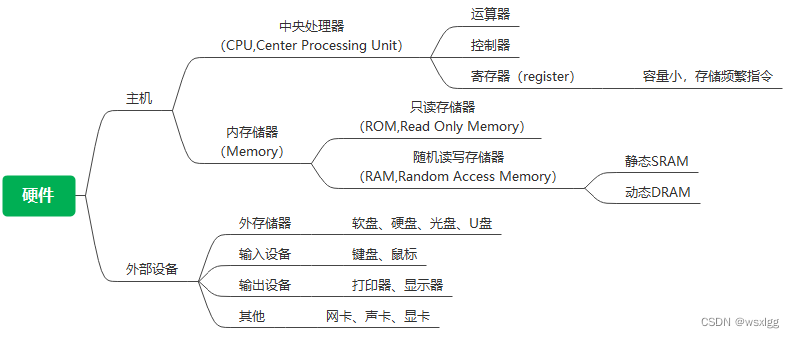
计算机中CPU、内存、缓存的关系
CPU(Central Processing Unit,中央处理器) 内存(Random Access Memory,随机存取存储器) 缓存(Cache) CPU、内存和缓存之间有着密切的关系,它们共同构成了计算机系统的核…...

【Linux实验】构造一个简单的 shell
一、实验目的 l 用 C/C++构造一个简单的 shell; l 理解 shell 程序的功能; l 学会 shell 的使用;...
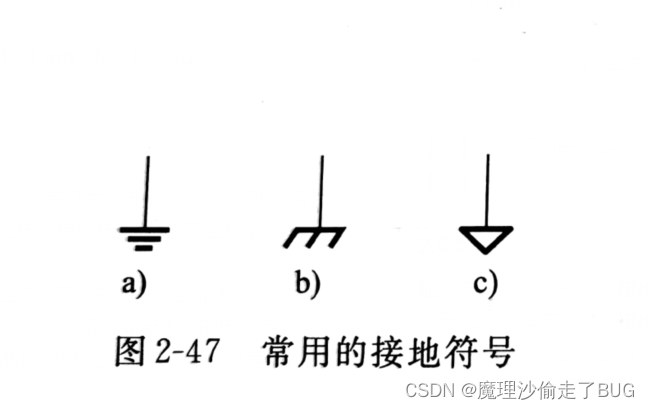
【电路原理学习笔记】第2章:电压、电流和电阻:2.6 电路
第2章:电压、电流和电阻 2.6 电路 2.6.1 电流的方向 电流方向有两种说法,一种按电子流动方向,另一种是传统的认为从正极流出到负极,这本教材采用传统电流方法。(事传统派,维新派输了,1&#…...

基于深度学习的人脸检测技术
用到环境 1、pycharm community edition 2022.3.2 2、Python 3.10 整篇内容都已上传至我的csdn资源中,想用的请移步。 流程 多任务级联卷积神经网络(Multi-task Cascaded Convolutional Networks, MTCNN)算法进行人脸检测 普通人脸检测 单人人脸检测 图1 单人人…...

【linux kernel】一文总结linux内核通知链
文章目录 1、通知链简介2、通知链的类型3、原理分析和API(1)注销通知器(2)注销通知器(3)通知链的通知 4、实例代码(1)定义一个通知链(2)实现观察者模块&#…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...
