图的总复习
一、图的定义Graph
图是由顶点vertex集合及顶点间关系集合组成的一种数据结构:
顶点的集合 和 边的集合
二、无向图
用(x,y)表示两个顶点x和y之间的一条边(edge)
边是无方向的
N={V,E},V={0,1,2,3,4,5} E={(0,1)......}
无向图有
一个有n个顶点的无向图最多有:
(n-1)n/2条边
如果一个无向图有(n-1)n/2条边
则称之为无向完全图。
邻接点:如果(x,y)属于E,称x和y互为邻接点,或x和y相邻接。
依附:边(x,y)依附于顶点x,y
相关联:边(x,y)与顶点x,y
顶点的度:与顶点x相关联的变的个数,记为TD(x)
三、有向图(Digragh)
用<x,y>表示从顶点x到顶点y之间的一条弧Arc
x为弧尾,y为弧头

四、网Network
网:带权的图被称为网
权:与弧或者边相关的数
五、
路径:是一个从顶点x到顶点y的序列
六、
回路
回路或环:路径的开始顶点与最后一个顶点相同
简单路径:在路径的顶点序列中,顶点不重复出现
七、连通
连通:如果顶点x到y有路径,称x和y是连通的
连通图:图中所有顶点都是连通的
八、子图
九、生成树
连通图的生成树是该图的一个极小连通子图。
设连通图有n个顶点,生成树也包含这n个顶点。
生成树有多少条边?n-1条
一、图的顺序存储结构




相关文章:

图的总复习
一、图的定义Graph 图是由顶点vertex集合及顶点间关系集合组成的一种数据结构: 顶点的集合 和 边的集合 二、无向图 用(x,y)表示两个顶点x和y之间的一条边(edge) 边是无方向的 N{V,E},V{0…...

测试流程记录
1,需求评审 2,技术方案评审 3,编写测试用例 编写需求分析 编写测试用例 编写冒烟case 4,用例评审 5,提测 提测前给开发执行冒烟case 6,测试 测试完成前约产品验收时间 7,验收 跟进验收问题…...

Mysql主从架构与实例
mysql的主从架构 MySQL主从架构是一种常见的数据库高可用性解决方案,它通常由一个主数据库和多个从数据库组成。主数据库用于处理写入请求和读取请求,从数据库则用于处理只读请求。 在主从架构中,主数据库记录所有数据更改并将这些更改同步…...

webpack(高级)--Tapable
webpack 我们直到webpack中有两个非常重要的类Compiler和Compilation 他们通过注入插件的方式 来监听webpack的所有声明周期 插件的注入是通过创建Tapable库中的各种Hook的实例来得到 Tapable Tapable中的Hook分为同步与异步 同步 SyncHook SyncBailHook SyncWaterfallHook…...

Python常见类型转换合集
近期在工作中常常接触到各种转换,如字符串转byte,byte转字符串,还有byte数组转成报文能接纳的格式(bin格式的十六进制)。故有必要系统的总结一下Python中常见的类型转换。 一:常见类型的概念 类型举例说明…...
)
知识点(1)
什么是跨域请求? 当前发起请求的域与该请求指向的资源所在的域不一样,凡是发送请求的url的协议、域名、端口号三者之间任意一者与当前页面地址不同的请求。这里的域指的是:我们认为若协议域名端口号均相同,那么就是同域。 get和…...
 Catalina启动)
Tomcat源码分析-启动分析(三) Catalina启动
在上一篇文章中,我们分析了tomcat的初始化过程,是由Bootstrap反射调用Catalina的load方法完成tomcat的初始化,包括server.xml的解析、实例化各大组件、初始化组件等逻辑。那么tomcat又是如何启动webapp应用,又是如何加载应用程序的…...
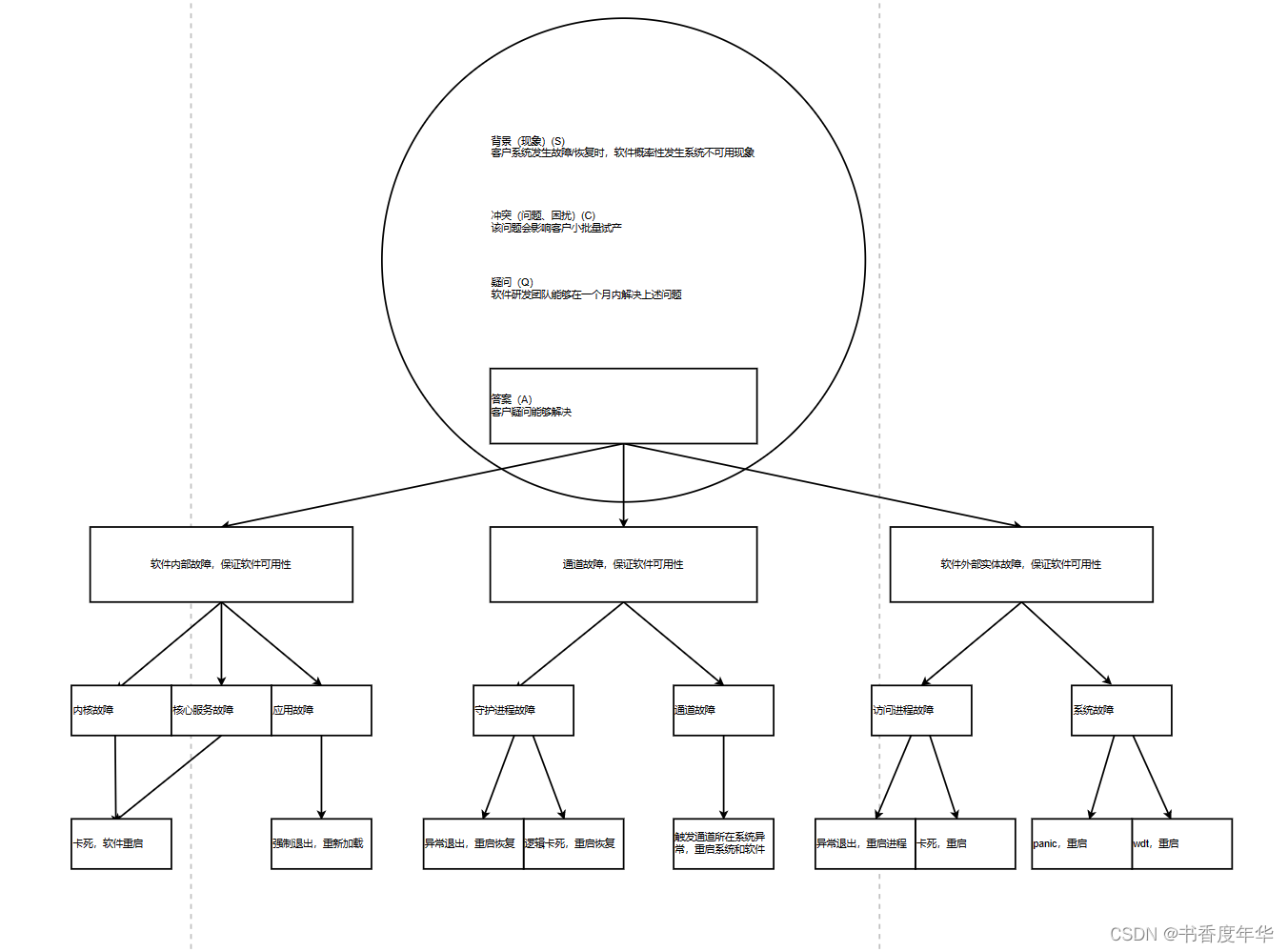
程序员必备的软技能-金字塔原理拆解
前言 日常工作中,常常因为思维、表达方式不对产生不想要的结果: 写了一个小时的周报,领导却不满意?跟团队讲了半天自己的想法,可别人就是没理解?看了很多知识、信息,却一点也没记住࿱…...
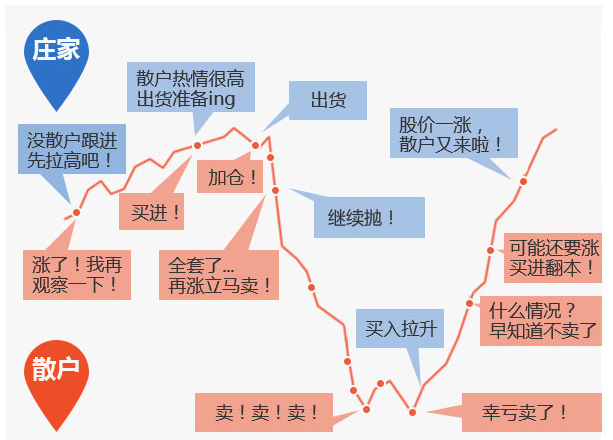
基金详细介绍
投资回报率 利润 / 投资总额(第一次投资回报率 5%) 关注南方理财 60 天债券 B(202306)万元收益 50—60 元 购基七步曲: 风险测试基本知识交易指南查看业绩了解评级在线下单赎回 基金类型: 积极成长型基金…...

媒体邀约之企业如何加强品牌的宣传力度
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。胡老师分享了许多媒体传播方面的经验,今天就跟大家分享下我对企业宣传方面的看法。企业如何加强品牌的宣传力度:1,网络宣传在社交媒体上建立企业账户&am…...

【SpringBoot】75、SpringBoot中使用spring-retry轻松解决重试
在日常开发过程中,难免会与第三方接口发生交互,例如:短信发送、远程服务调用、争抢锁等场景,当正常调用发生异常时,例如:网络抖动,这些间歇性的异常在一段时候之后会自行恢复,程序为…...

网络工程师必知的几个问题
路由器问题: 1、什么时候使用多路由协议? 当两种不同的路由协议要交换路由信息时,就要用到多路由协议。当然,路由再分配也可以交换路由信息。下列情况不必使用多路由协议: 从老版本的内部网关协议( interi…...
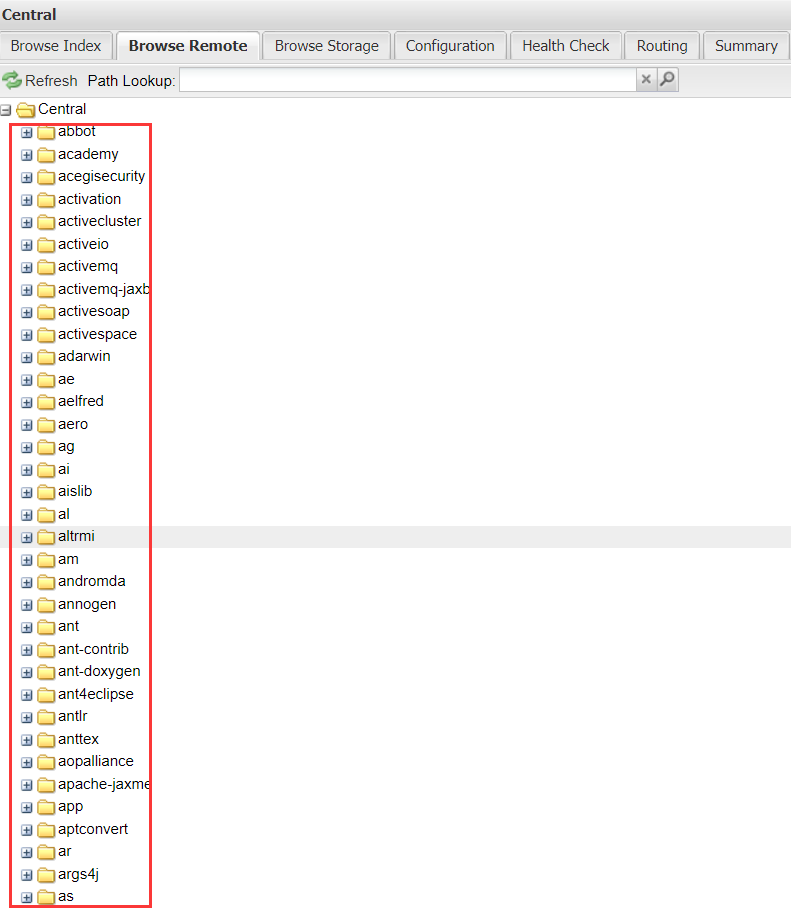
【仓库管理】搭建 Maven 私服之一--Nexus仓库(Repository)管理软件
文章目录Nexus是什么Nexus下载和安装1. 进入 Nexus 2.x 下载页面,根据本机操作系统,选择对应的版本进行下载,如下图所示。2. 将下载 Nexus 安装包解压到本地磁盘,可获得 nexus-2.14.20-02 和 sonatype-work 2 个目录,如…...
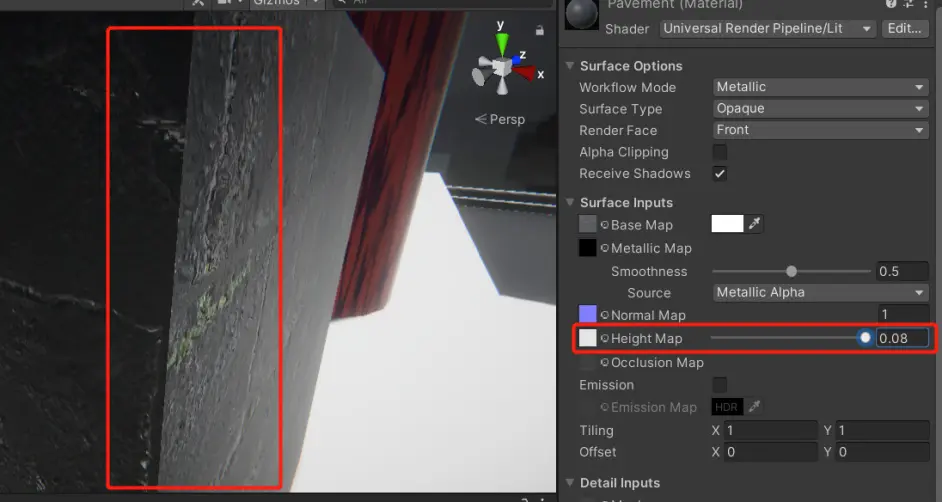
凹凸贴图(Bump Mapping)
凹凸贴图是什么? 我们首先来看low-poly(多边形数较少)mesh和high-poly(多边形数量较多)mesh之间的不同。首先,最明显的不同就是high-poly能够表现出更多细节,但high-poly有比较大的性能开销。有…...
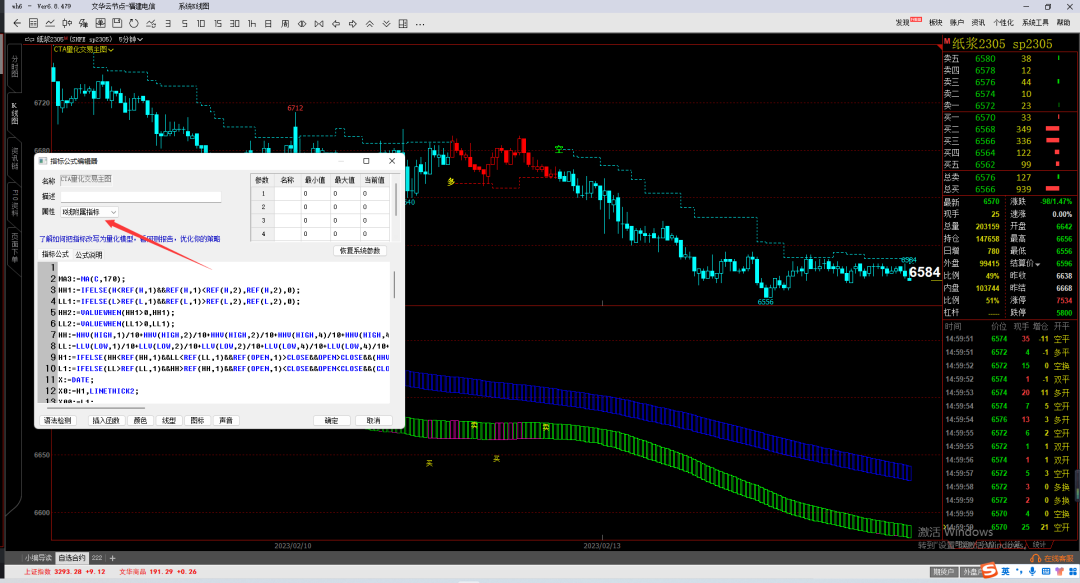
文华财经期货指标公式量化策略分析软件,多空共振信号准确率高的公式源码
期货指标公式信号本身就有滞后性,周期越大,滞后性越久。指标公式不是100%稳赚的工具,只是在合适的时候让我们理性看待行情,减少逆势操作。 多空量化三维系统是一款通过数学分析、挖掘价格运动规律,对历史价格走势、趋势…...
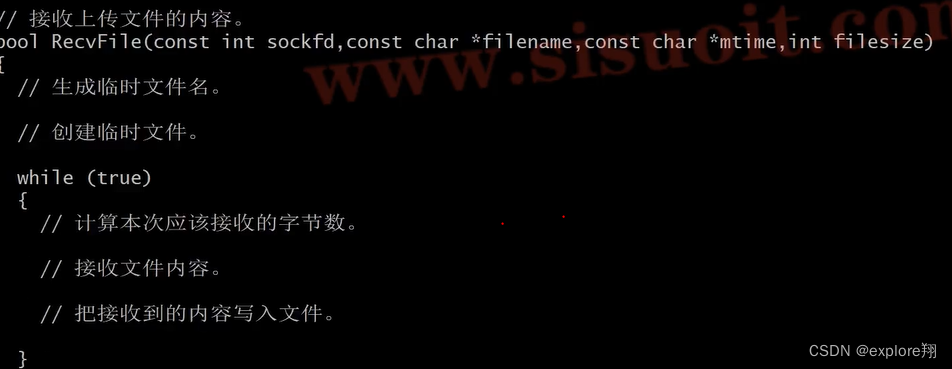
基于TCP协议的文件传输系统
最简单的一对一的服务端网络端通信(socket) Socket(IP地址:端口号),例如:如果IP地址是210.37.145.1,而端口号是23,那么得到套接字就是(210.37.145.1:23) socket可以理解成计算机提供给程序员的接…...

Linux定时备份MySql数据库
一、创建文件 cd / mkdir mysqlbackup vi mysqlbackup.sh然后将下面的代码更改后复制上去即可。 #!/bin/bash mysqldump -uroot -ppassword database > /mysqlbackup/database__$(date %Y%m%d_%H%M%S).sqlpassword指的是MySql的密码,database指的是所要备份的…...
)
JavaScript prototype(原型对象)
JavaScript 的原型(prototype)是 JavaScript 中的一个重要概念。它是一种特殊类型的对象,每个 JavaScript 对象都有一个原型对象。原型对象在 JavaScript 中起着非常重要的作用。本文将详细介绍 JavaScript 原型对象的作用和在实际工作中的用…...
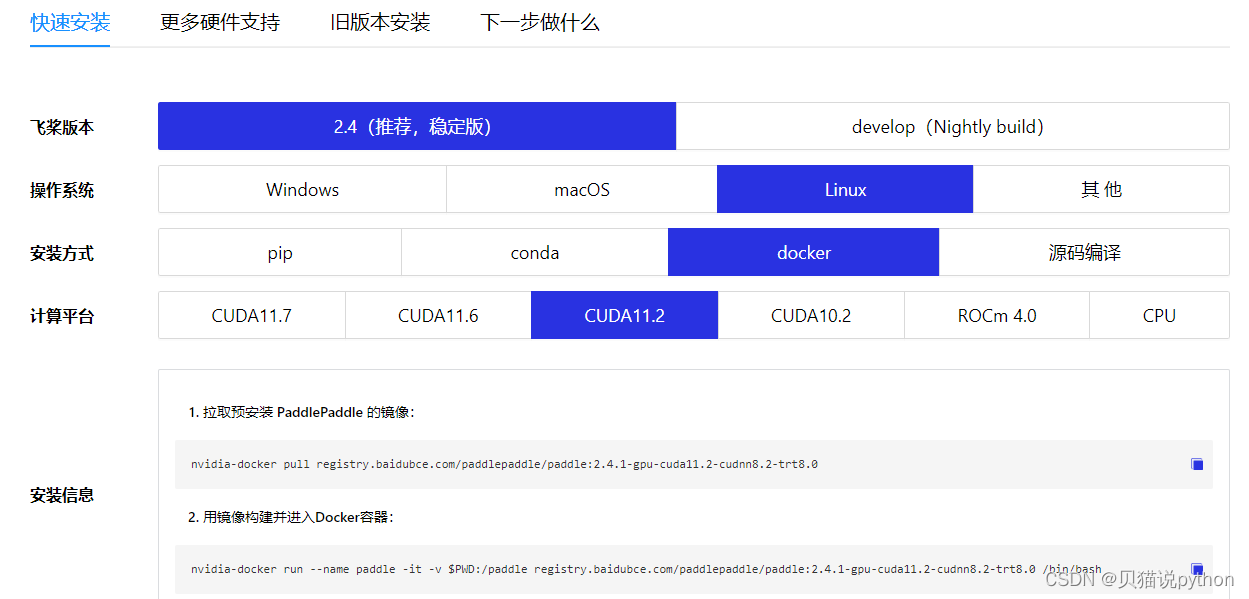
pytorch各种版本最简单安装,不用自己安装cuda cudnn
pytorch各种版本 pip 安装命令 查看官网 https://pytorch.org/get-started/previous-versions/ conda pytorch 安装 1、安装conda, 2、创建并并激活虚拟环境 - conda create -n pytorch_1.7 python3.7 - conda activate pytorch_1.7 3、虚拟环境中 pip 安装想要的…...
订单超时处理方案介绍
在电商场景下,一个订单流程中有许多环节要用到超时处理,包括但不限于: 买家超时未付款:比如超过15分钟没有支付,订单自动取消。 商家超时未发货:比如商家超过1个月没发货,订单自动取消。 买家…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
