C国演义 [第三章]
第三章
- 组合
- 分析
- 步骤
- 递归函数的返回值和参数
- 递归结束的条件
- 单层逻辑
- 组合总和 III
组合
力扣链接
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
- 提示:
1 <= n <= 20
1 <= k <= n
分析
暴力解法当然是用 for循环 :
n = 4, k = 2时:
int n = 4;
for (int i = 1; i <= n; i++) {for (int j = i + 1; j <= n; j++) {cout << i << " " << j << endl;}
}
n = 100, k = 3时:
int n = 100;
for (int i = 1; i <= n; i++) {for (int j = i + 1; j <= n; j++) {for (int u = j + 1; u <= n; n++) {cout << i << " " << j << " " << u << endl;}}
}
如果 k = 50呢? 就要用50个for循环. 有一个问题; 我们如何控制 50 个for循环呢
为了解决这种情况: 我们采用 回溯
回溯也是一种暴力, 但是可以用递归次数来解决for循环的层数
🗨️它是如何解决for循环的层数呢?
- 递归里面套用for循环 — — 每一次递归套用一个for循环, 那么我们解决递归的层数来控制for循环的层数
过程是非常抽象的, 但是递归的过程可以用 二叉树来做一个形象的理解
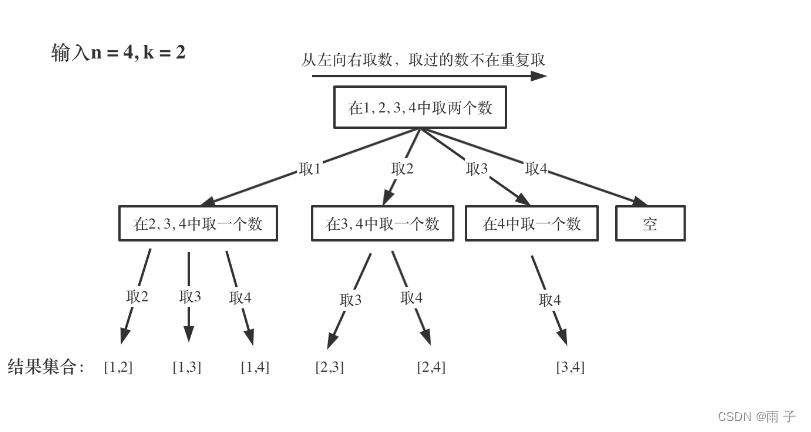
先看一个分支(纵向):
集合是 [1, 2, 3, 4], 从中任选一个 , 以取 1 为例子
然后集合是 [2, 3, 4], 从中任选一个就已经达到目标了, [1, 2], [1, 3], [1, 4]
集合是[1, 2, 3, 4], 从中任选一个, 以取 2 为例子
然后集合是 [3, 4], 从中任选一个就已经达到目标了, [2, 3], [2, 4]
集合是[1, 2, 3, 4], 从中任选一个, 以取 3为例子
然后集合是[ 4 ], 从中任选一个就已经达到目标了, [3, 4]
集合是[1, 2, 3, 4], 从中任选一个, 以取 4为例子
然后集合是[ ], 就不能继续递归下去了
🗨️为啥集合是 [1, 2, 3, 4], 取 2, 然后剩余集合是 [3, 4]. 为啥不是[1. 3. 4 ]?
- 因为求的是
组合, 所以不用注意相同数值的顺序
如果剩余集合是 [1, 3, 4], 那么叶子结点就是 [2, 1], [2, 3], [2, 4]
这个时候, [1, 2] 和 [2, 1] 是重复的
⇒所以我们需要一个变量来控制下一层递归的开头
每次从集合中选取元素, 下一层递归的范围随着选取元素而缩减
步骤
递归函数的返回值和参数
一般回溯的返回值都是 void, 除非有特殊要求
需要定义两个全局变量, 一个来记录单层结果, 一个来记录全部结果
vector<int> path; // 记录单层结果
vector<int<vector<int>> result; // 记录全部结果
虽然这两个变量也可以放在参数列表里面, 但是这会导致参数列表过于冗杂, 而看不清回溯的逻辑
数组大小n 和 结果大小k 肯定是在参数列表中的
为了避免结果有重复的, 需要有一个变量来控制每一层递归的区间集合(开头), 我们一般用 startindex
⇒ 所以我们的递归函数应该如下:
vector<int> path;
vector<vector<int>> result;
void backtracking(int n, int k, int startindex )
递归结束的条件
path是用来记录单层结果的, 根据题目要求,
递归结束的条件是: path的大小是2
那么我们就把path收入result里面, 并不继续向下递归
if(path.size()) == k){result.push_back(path);return;}
单层逻辑
单层逻辑肯定是一个for循环
for循环的起始点是 startindex, 终止点是 n
for(int i = startindex; i <= n; i++ ){}
我们先把沿途的数值收入path
for(int i = startindex; i <= n; i++ ){path.push_back(i);}
继续向下递归, 此时的起始点就变成 i + 1
for(int i = startindex; i <= n; i++ ){path.push_back(i);backtracking(n, k, i + 1);}
回溯, 让一棵树的情况更加完整
for(int i = startindex; i <= n; i++ ) // 控制横向遍历{path.push_back(i); // 处理节点backtracking(n, k, i + 1); // 纵向递归path.pop_back(); // 回溯, 撤销处理的节点}```## 代码```cpp
class Solution {
public:vector<vector<int>> result;vector<int> path;void backtracking(int n, int k, int startindex){// 终止条件if(path.size() == k){result.push_back(path);return ;}// 单层逻辑for(int i = startindex; i <= n; i++){path.push_back(i);backtracking(n, k, i + 1);path.pop_back(); // 回溯}}vector<vector<int>> combine(int n, int k) {backtracking(n, k, 1);return result;}
};

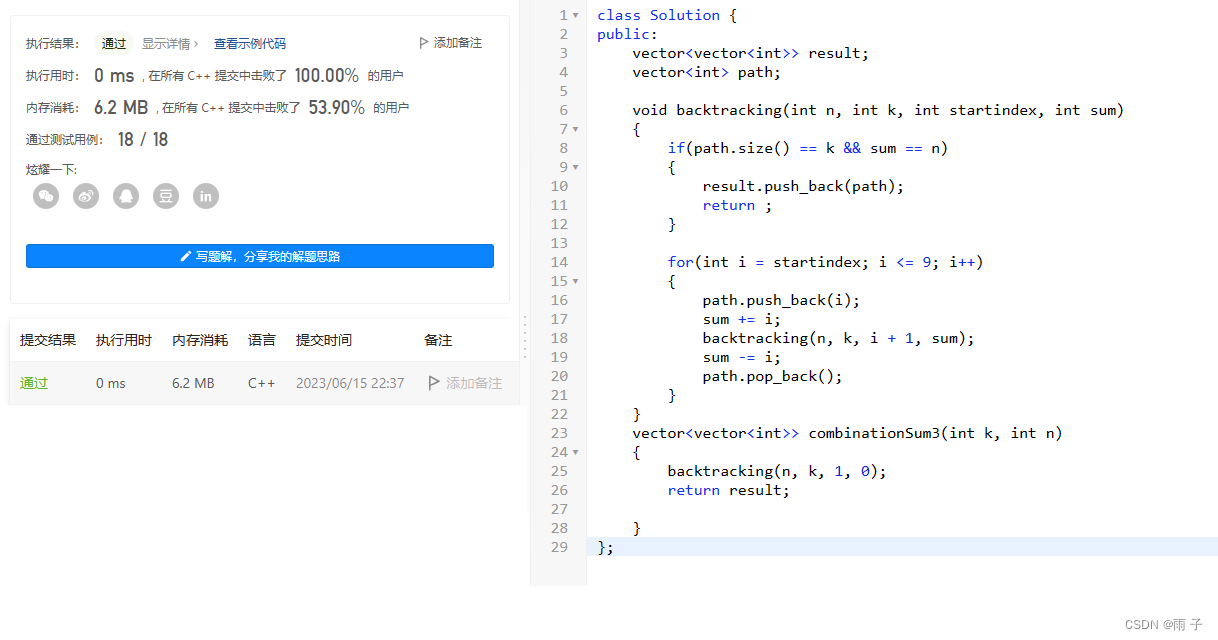
组合总和 III
力扣链接
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。
示例 3:
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。
- 提示:
2 <= k <= 9
1 <= n <= 60
class Solution {
public:vector<vector<int>> result;vector<int> path;void backtracking(int n, int k, int startindex, int sum){if(path.size() == k && sum == n){result.push_back(path);return ;}for(int i = startindex; i <= 9; i++){path.push_back(i);sum += i;backtracking(n, k, i + 1, sum);sum -= i;path.pop_back();}}vector<vector<int>> combinationSum3(int k, int n) {backtracking(n, k, 1, 0);return result;}
};
相关文章:

C国演义 [第三章]
第三章 组合分析步骤递归函数的返回值和参数递归结束的条件单层逻辑 组合总和 III 组合 力扣链接 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回答案。 示例 1: 输入:n 4, k 2 输出࿱…...
数字化时代,企业的数据指标体系
在社会节奏越来越快,处理的信息量越来越大的今天,传统的经营管理模式已经适应不了当下的环境。而由经验、情感组成的业务调整以及决策能力不再能正确指导企业走在正确的方向上,所以数据就成为了企业新的业务优化调整和支撑企业高层管理进行决…...
三分钟了解 RocketMQ消息队列
文章目录 基本概念详细介绍主题(Topic)消息类型(MessageType)消息队列(MessageQueue)消息(Message)消息视图(MessageView)消息标签(MessageTag&am…...

golang redis第三方库github.com/go-redis/redis/v8实践
Redis基本数据类型代码示例# 这里示例使用 go-redis v8 ,不过 go-redis latest 是 v9 安装v8:go get github.com/go-redis/redis/v8 Redis 5 种基本数据类型: string 字符串类型;list列表类型;hash哈希表类型&#…...
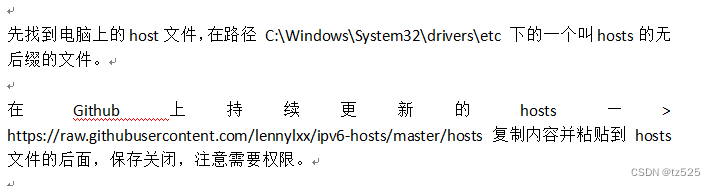
校园网WiFi IPv6免流上网
ipv6的介绍 IPv6是国际协议的最新版本,用它来取代IPv4主要是为了解决IPv4网络地址枯竭的问题,也在其他很多方面对IPv4有所改进,比如网络的速度和安全性。 IPv4是一个32位的地址,随着用户的增加在2011年国家报道说IPv4的网络地址即…...
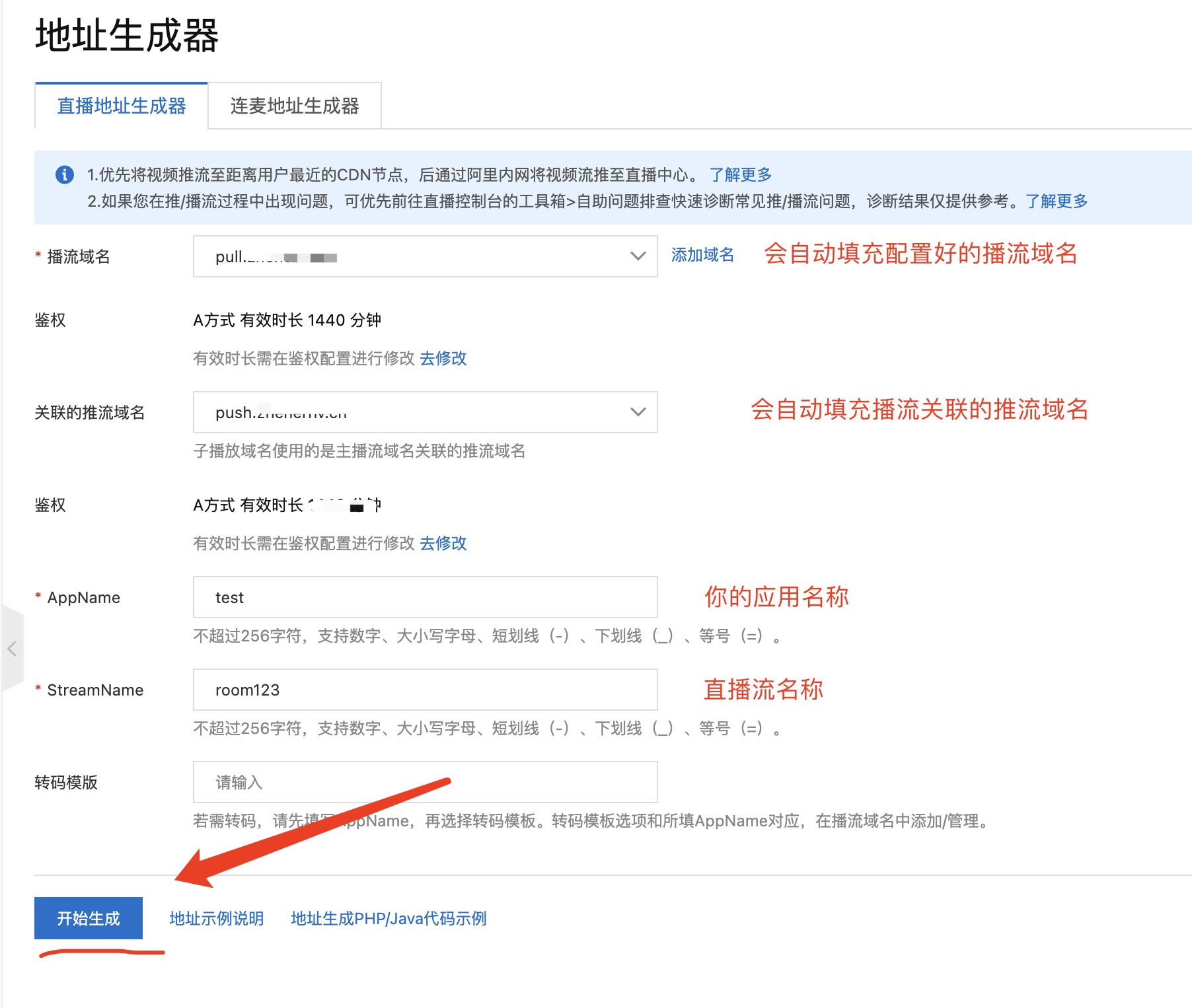
java 阿里云直播配置及推拉流地址获取
一、开通阿里云直播 首先进入阿里云直播产品主页:https://www.aliyun.com/product/live 。 点击下方的“立即开通”。 如果是还未注册的用户请按照页面提示进行完成注册并实名认证。 2、首次进入会提示开通服务,点击“开通服务”,然后选择计…...

PostgreSql 限制
参考:https://www.postgresql.org/docs/current/limits.html 项目上限说明单个数据库尺寸无限制null单个实例中数据库数量4,294,950,911null单个数据库中关系数量1,431,650,303null单个关系尺寸32 TB数据块为8k时单个表行数受4,294,967,295页的元组数量限制null单个…...

2023年java还是golang还是c#?
前言 我们可以先来看一下这三门语言各自的优劣 学习曲线:如果你是初学者或对编程相对陌生,Java可能是一个较好的选择。它有广泛的学习资源和社区支持,易于上手。Go也有简单易学的特点,但由于相对较年轻,相关的学习资…...

微服务、SpringBoot、SpringCloud 三者的区别
🎈 作者:Linux猿 🎈 简介:CSDN博客专家🏆,华为云享专家🏆,Linux、C/C、云计算、物联网、面试、刷题、算法尽管咨询我,关注我,有问题私聊! &…...
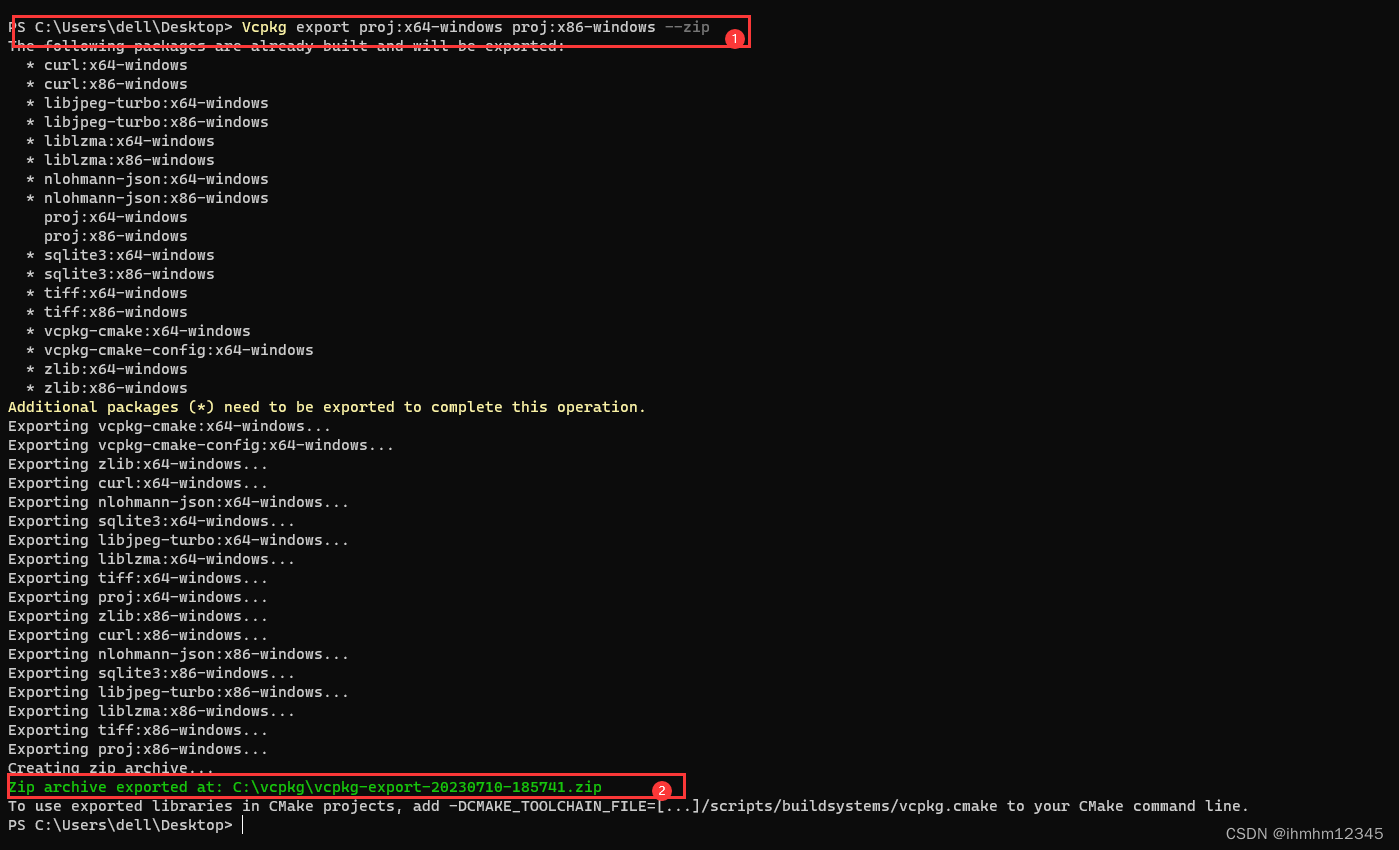
2023-07-10 cmake管理的项目中使用vcpkg管理第三方库
一、安装 从Github上克隆Vcpkg仓库然后执行安装命令即可: git clone https://github.com/microsoft/vcpkg .\vcpkg\bootstrap-vcpkg.bat 安装自己需要的第三方库 .\vcpkg\vcpkg install [packages to install] 更多教学可参考: https://learn.microsoft…...
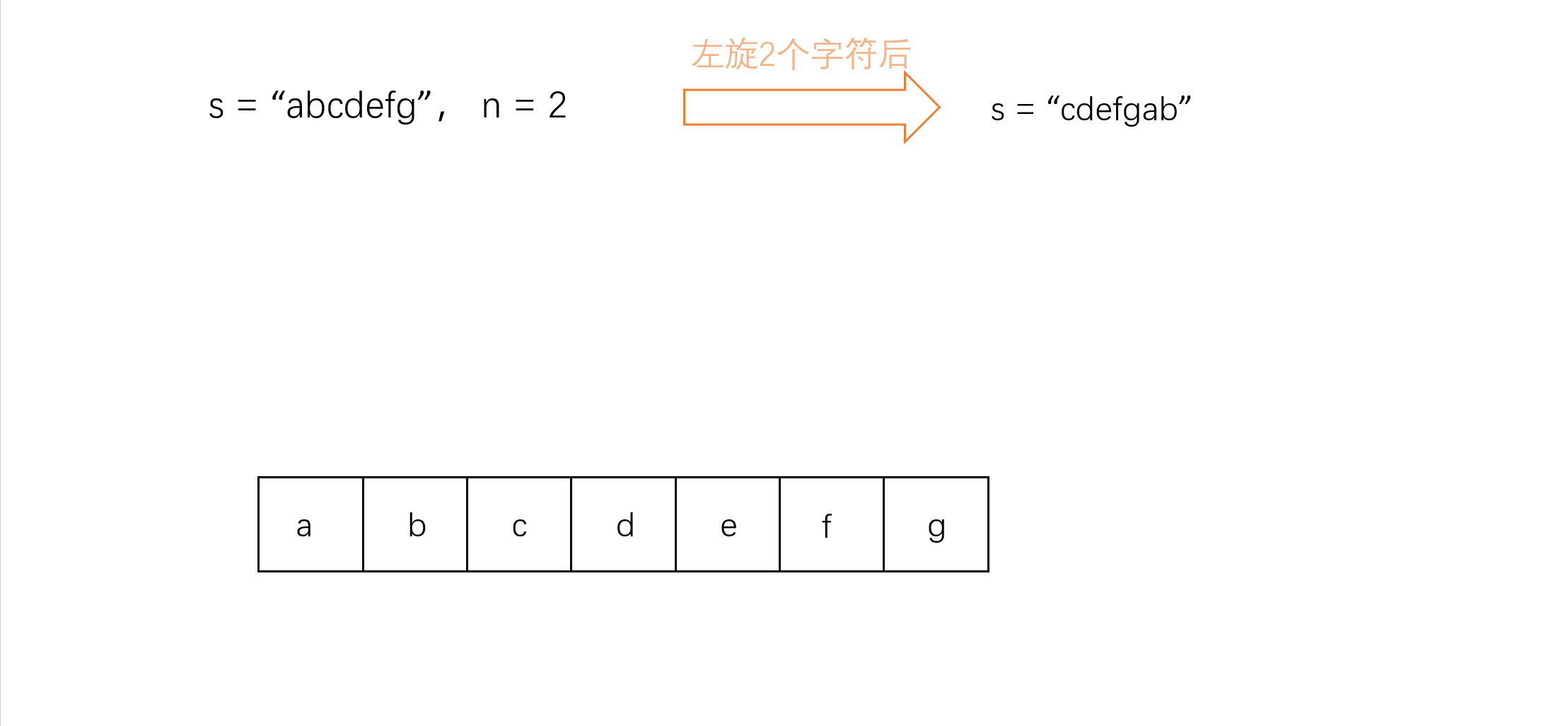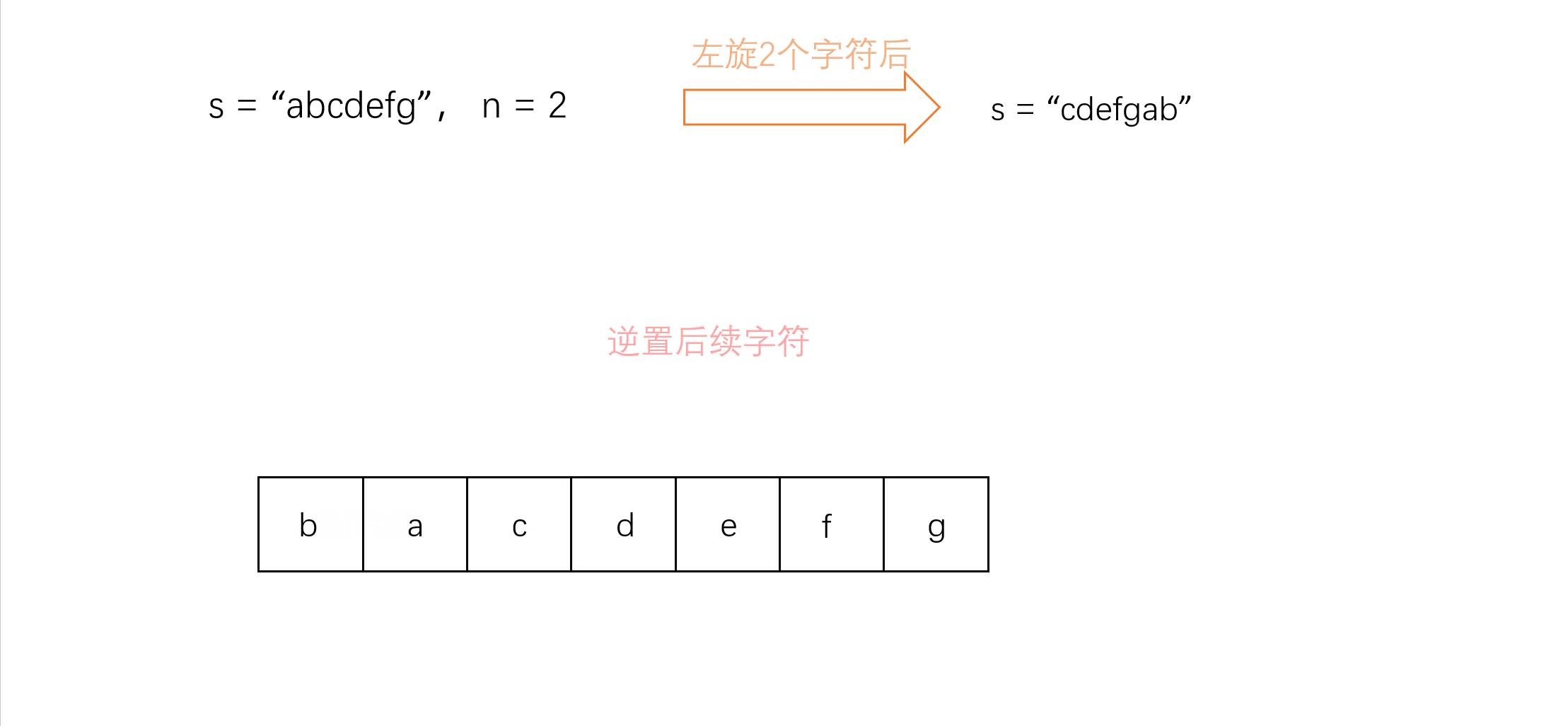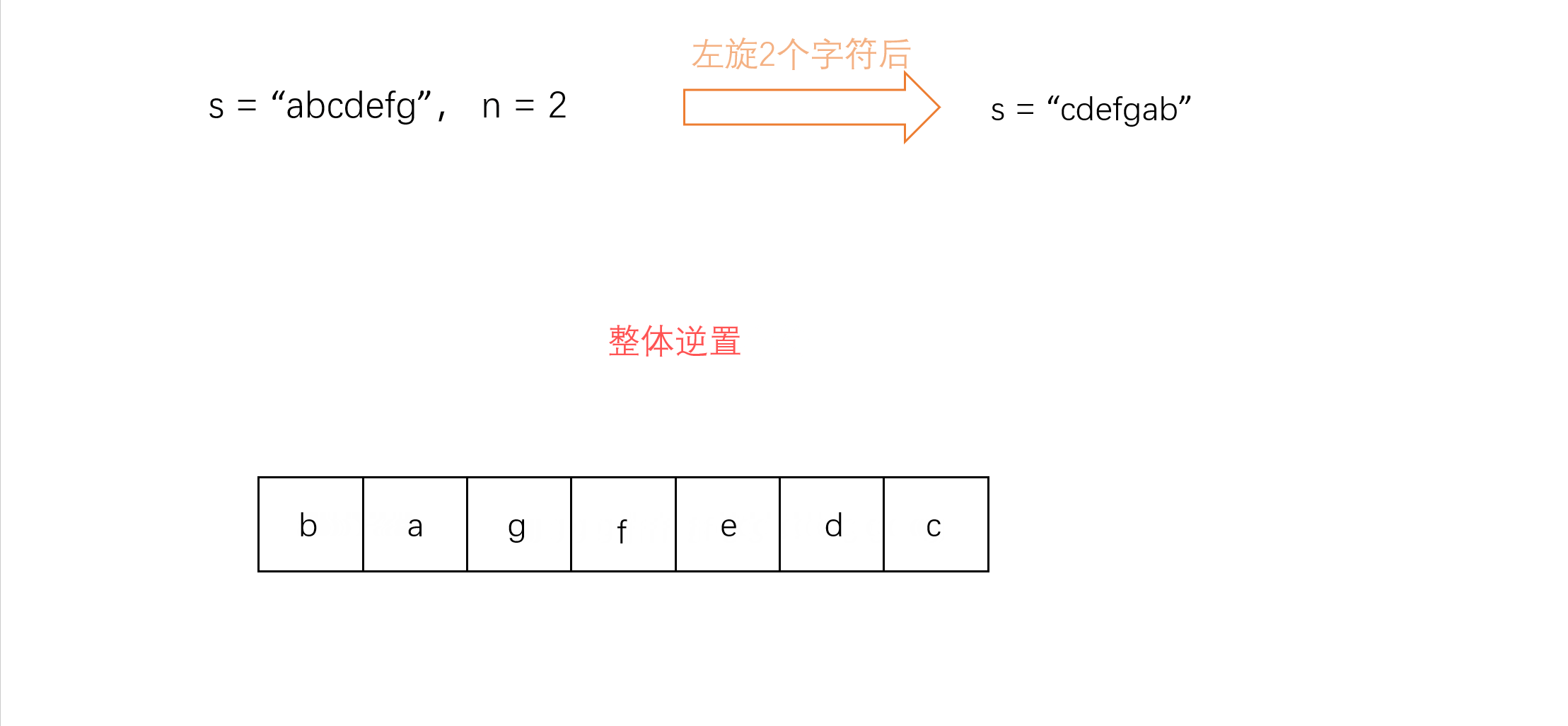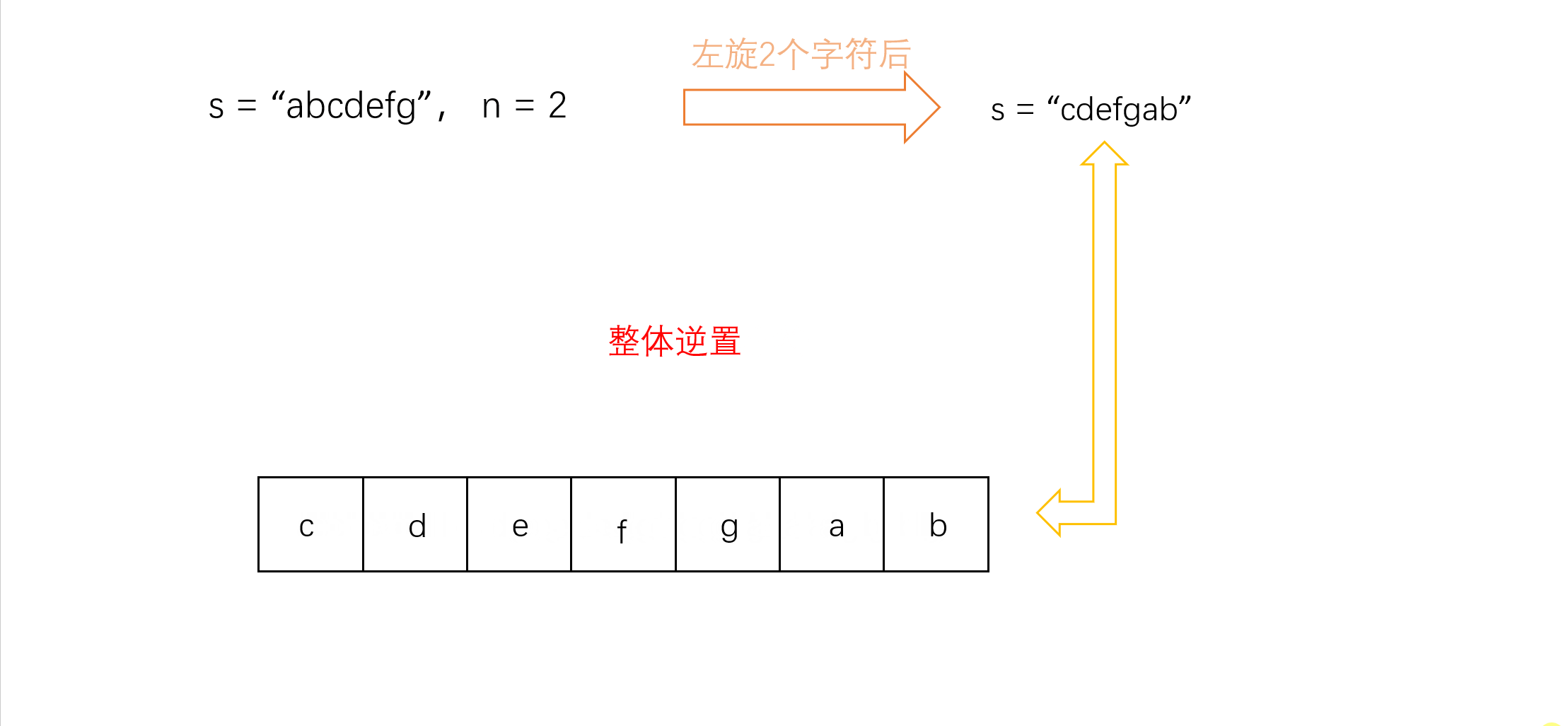
【剑指offer】学习计划day3
目录 一. 前言 二.替换空格 a.题目 b.题解分析 c.AC代码 三. 左旋转字符串 a.题目 b.题解分析 c.AC代码 一. 前言 本系列是针对Leetcode中剑指offer学习计划的记录与思路讲解。详情查看以下链接: 剑指offer-学习计划https://leetcode.cn/stud…...

QT DAY1
做一个窗口界面 #include "mainwindow.h" #include "ui_mainwindow.h"MainWindow::MainWindow(QWidget *parent) :QMainWindow(parent),ui(new Ui::MainWindow) {ui->setupUi(this);//设置窗口标题、图标this->setWindowTitle("Fly_Chat")…...
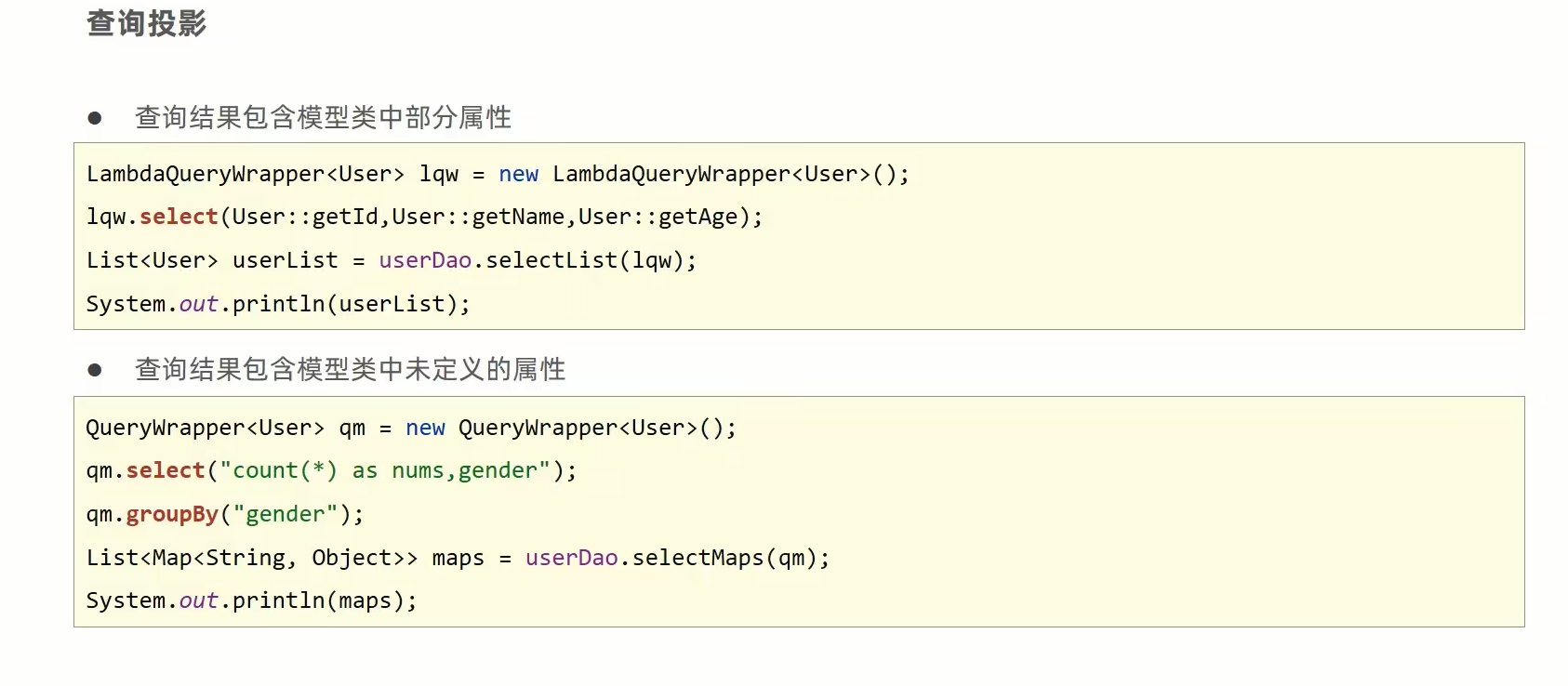
Mybatis-puls——条件查询的三种格式+条件查询null判定+查询投影
前言 在mybatis_plus的封装中的Wrapper<T>接口参数就是用于封装查询条件 在测试类中启动如上一个简单的查询,然后控制台运行会输出一大堆无关日志,这里先把这些日志关闭 去除无关日志文件 先新建一个XML配置文件 然后变成如下,这里…...

网络安全(黑客)自学
建议一:黑客七个等级 黑客,对很多人来说充满诱惑力。很多人可以发现这门领域如同任何一门领域,越深入越敬畏,知识如海洋,黑客也存在一些等级,参考知道创宇 CEO ic(世界顶级黑客团队 0x557 成员…...
的用法【数据表“一对一”关系】)
通过一个实际例子说明Django中的数据库操作方法OneToOneField()的用法【数据表“一对一”关系】
当我们在Django中定义一个模型时,可以使用OneToOneField来建立一个一对一的关系。这种关系表示两个模型之间的一种特殊关联,其中一个模型的实例只能与另一个模型的实例关联。 让我们以一个简单的示例来说明OneToOneField的用法。假设我们正在构建一个简…...

HarmonyOS学习路之开发篇—数据管理(对象关系映射数据库)
HarmonyOS对象关系映射(Object Relational Mapping,ORM)数据库是一款基于SQLite的数据库框架,屏蔽了底层SQLite数据库的SQL操作,针对实体和关系提供了增删改查等一系列的面向对象接口。应用开发者不必再去编写复杂的SQ…...

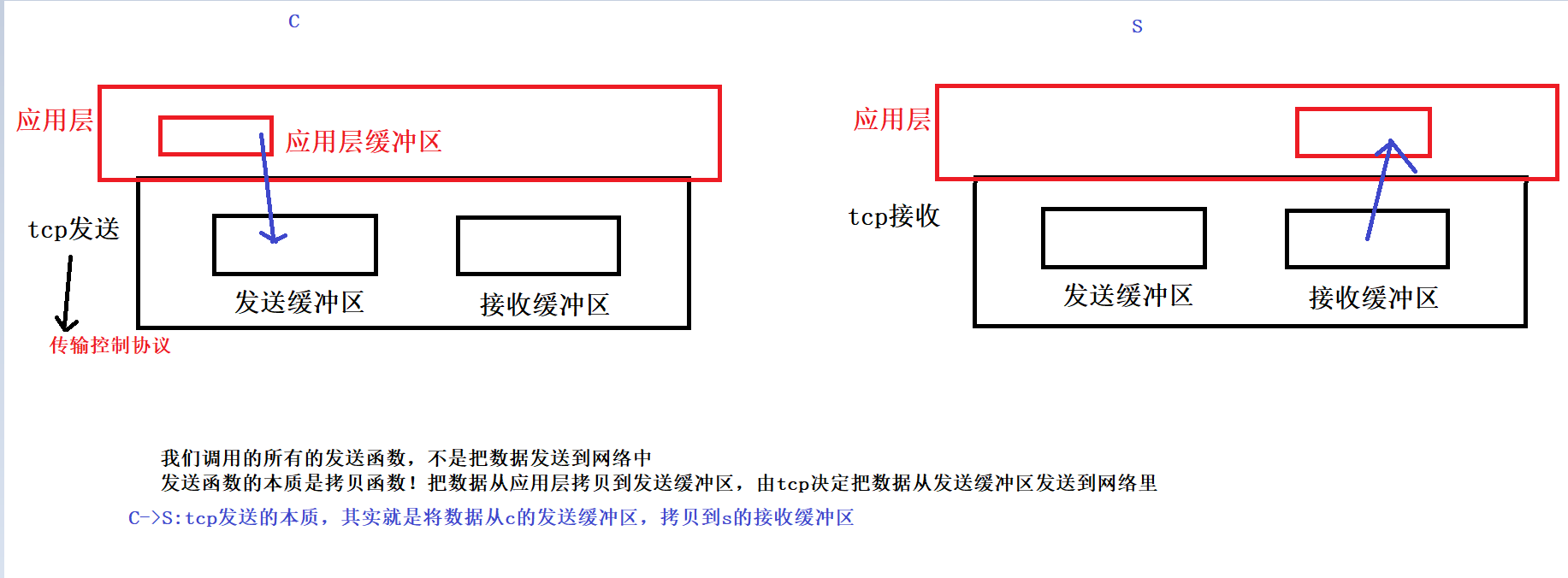
实验:验证TCP套接字传输的数据不存在数据边界
来源:《TCP/IP网络编程》 学习ing 自己动手,把坑踩一遍,也可以学习到很多。 Linux环境下: 客户端: #include <stdio.h> #include <stdlib.h> #include <string.h> #include <unistd.h> #include <…...
【网络】协议的定制与Json序列化和反序列化
文章目录 应用层初识TCP协议通讯流程定制协议再谈协议网络版本计算器Protocal.hppCalServerCalClient Json的安装 应用层 我们程序员写的一个个解决我们实际问题, 满足我们日常需求的网络程序, 都是在应用层 初识TCP协议通讯流程 建立链接和断开链接 基于TCP协议,…...

浙大数据结构第一周最大子列和问题
题目详情: 给定K个整数组成的序列{ N1, N2, ..., NK },“连续子列”被定义为{ Ni, Ni1, ..., Nj },其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 }ÿ…...
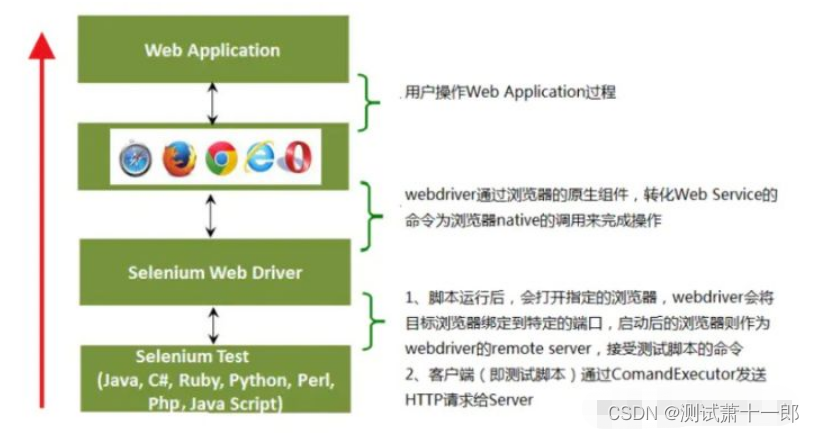
Selenium基础 — Selenium自动化测试框架介绍
1、什么是selenium Selenium是一个用于Web应用程序测试的工具。只要在测试用例中把预期的用户行为与结果都描述出来,我们就得到了一个可以自动化运行的功能测试套件。Selenium测试套件直接运行在浏览器中,就像真正的用户在操作浏览器一样。Selenium也是…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
