Matlab数学建模实战——(Lokta-Volterra掠食者-猎物方程)
1.题目

问题1
该数学建模的第一问和第二问主要是用Matlab求解微分方程组,直接编程即可。
求解
Step1改写
- y(1)=r
- y(2)=f
Step2得y的导数
- y(1).=2y(1)-ay(1)*y(2)
- y(2).=-y(2)+a*y(1)*y(2)
Step3编程
clear;
a=0.01;
F=@(t,y)[2*y(1)-a*y(1)*y(2);-y(2)+a*y(1)*y(2)];
[t,y]=ode45(F,[0,10],[300,150]);
subplot(121);
plot(t,y(:,1));
xlabel('时间');
ylabel('r数量');
subplot(122);
plot(y(:,1),y(:,2));
xlabel('r数量');
ylabel('y数量');
Step4结果
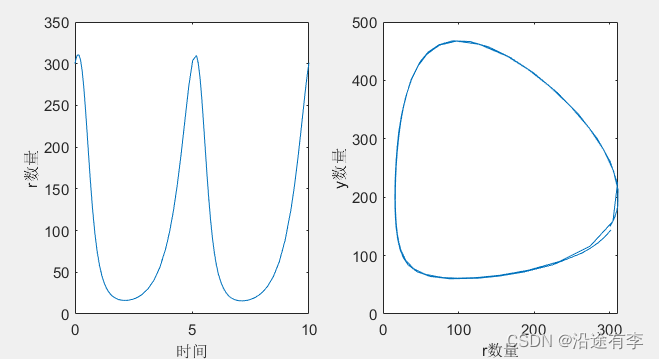
从图中可以看出对应的周期tp大概是5
问题2
改变初值就行啦,直接进入step3
求解
Step3编程
clear;
a=0.01;
F=@(t,y)[2*y(1)-a*y(1)*y(2);-y(2)+a*y(1)*y(2)];
[t,y]=ode45(F,[0,10],[15,22]);
subplot(121);
plot(t,y(:,1));
xlabel('时间');
ylabel('r数量');
subplot(122);
plot(y(:,1),y(:,2));
xlabel('r数量');
ylabel('y数量');
Step4结果
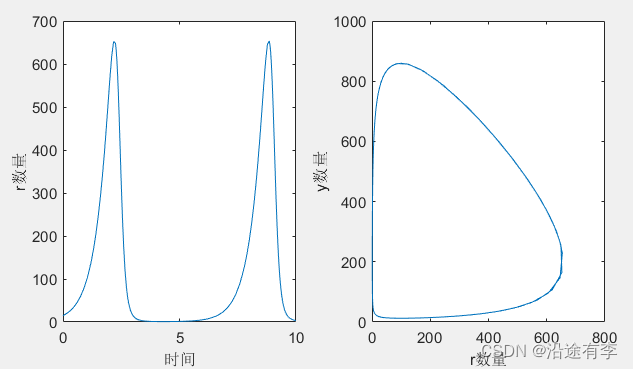
从图中可以看出对应的周期tp大概是8
问题3
分析
首先列公式,给了u和v的定义,咱就对它求导,然后把它代入捕食者方程,再把r和f用u和v替换,根据题目所说忽略二阶项uv,这样可以算得
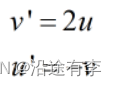
求解
Step1改写
- y(1)=u
- y(2)=v
Step2得y的导数
- y(1).=-y(2)
- y(2).=2y(1)
Step3编程
clear;
a=0.01;
F=@(t,y)[-y(2);2*y(1)];
[t,y]=ode45(F,[0,10],[0.1,0.1]);
subplot(121);
plot(t,y(:,1));
xlabel('时间');
ylabel('u');
subplot(122);
plot(y(:,1),y(:,2));
xlabel('u');
ylabel('v');
Step4结果
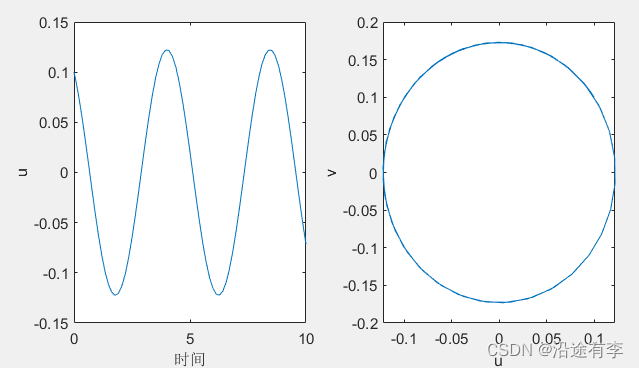
从图中可以看出u对应的周期tp大概是5
相关文章:

Matlab数学建模实战——(Lokta-Volterra掠食者-猎物方程)
1.题目 问题1 该数学建模的第一问和第二问主要是用Matlab求解微分方程组,直接编程即可。 求解 Step1改写 y(1)ry(2)f Step2得y的导数 y(1).2y(1)-ay(1)*y(2)y(2).-y(2)a*y(1)*y(2) Step3编程 clear; a0.01; F(t,y)[2*y(1)-a*y(1)*y(2);-y(2)a*y(1)*y(2)]; […...

windows下软件推荐
起源与目的 选择任何一个系统作为主力系统都是要好好考虑的。 在去年新买了一块1T的SSD后,就好好想了想这个问题。 Arch Linux, Ubuntu, Windows, macOS, deepin都是在考虑范围的。 不过我考虑到使用体验,最终还是选择了windows。 不选择macOS主要是不喜…...

SQlite数据库
SQlite数据库 1.SQLite简介 轻量化,易用的嵌入式数据库,用于设备端的数据管理,可以理解成单点的数据库。传统服务器型数据库用于管理多端设备,更加复杂 SQLite是一个无服务器的数据库,是自包含的。这也称为嵌入式数…...

Doris-问题
1.启动BE报错 设置系统最大打开文件句柄数(注意这里的*不要去掉) 重启生效!!!重启生效!!!重启生效!!! sudo vim /etc/security/limits.conf * soft nofile 65536 * hard nofile 65536 * soft nproc 131072 * hard nproc 131072 重启生效...

什么是OA系统,什么是工单系统,有啥区别?
一、OA系统与工单系统介绍 1、什么是OA系统 OA系统全称为Office Automation,即办公自动化系统。它是一种专门为企业和机构的日常办公工作提供服务的综合性软件平台,具有信息管理、流程管理、知识管理(档案和业务管理)、协同办公…...

DDoS攻击:网络安全的威胁
什么是DDoS攻击? DDoS(分布式拒绝服务)攻击是一种恶意网络攻击,目的是通过发送大量的请求或占用目标系统的资源,使其无法正常运行。在DDoS攻击中,攻击者使用分布在多个地理位置的多台计算机(也称…...

docker版jxTMS使用指南:device的调整
本文讲解4.2版jxTMS对device的调整,整个系列的文章请查看:docker版jxTMS使用指南:4.2版升级内容 docker版本的使用,请参考docker版jxTMS使用指南 4.0版jxTMS的说明,请查看:4.0版升级内容 为了适应拉取模…...

AI智能语音机器人的功能和作用都有哪些?
智能语音机器人是一种能够使用自然语言处理技术和人工智能算法,通过声音与用户进行交互的机器人。它可以回答用户提出的问题、处理用户的投诉、提供产品或服务的相关信息等等。 实现一个智能语音机器人需要涉及多个技术领域,包括自然语言处理、语音识别…...
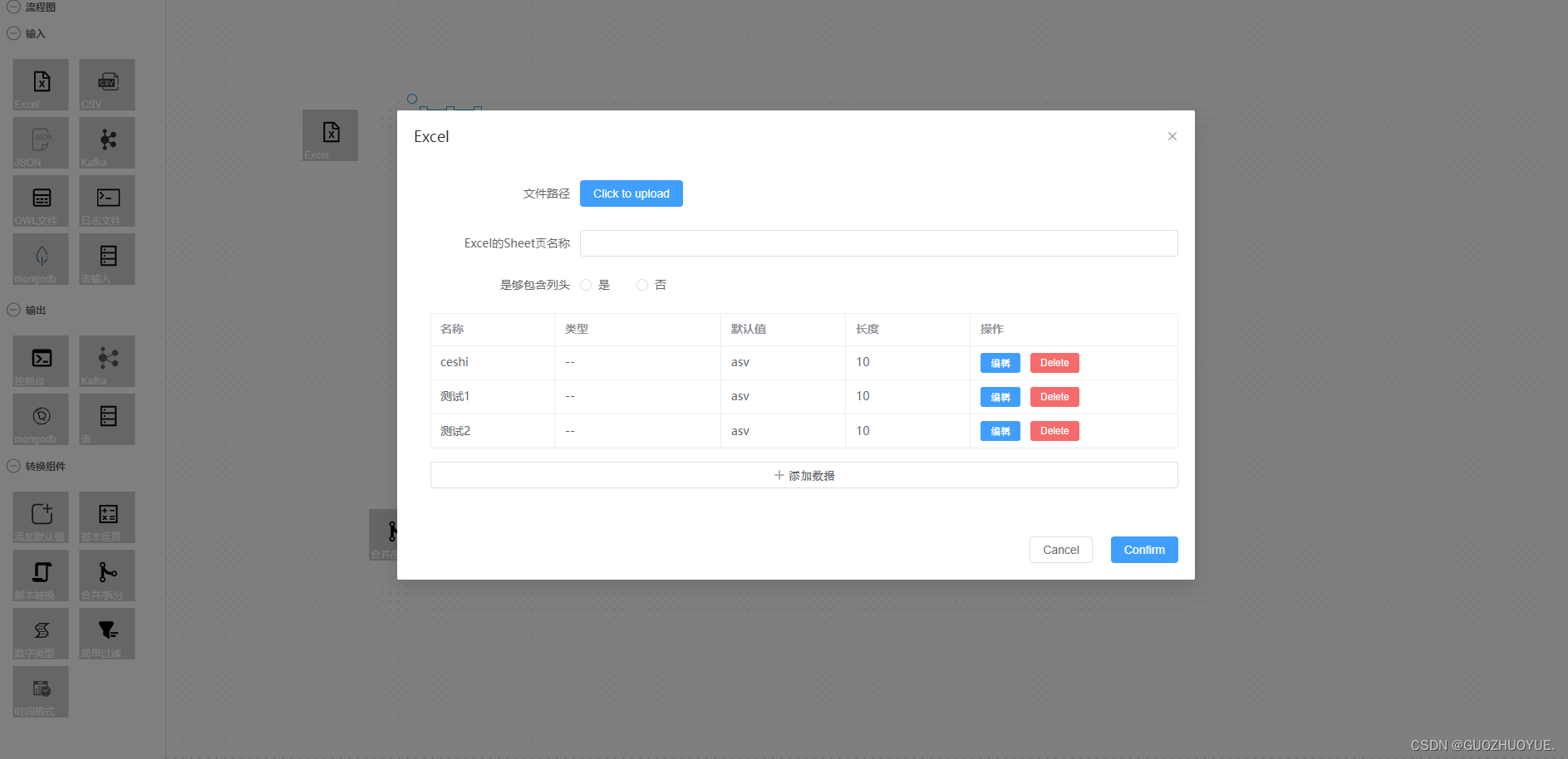
vue3+vite+Ts 基于Antv/x6 绘制流程图
需求效果: 需求: 实现一个流程图,双击可对相应的组件进行一些功能操作; 工具栈: 这里使用antv/x6, 基于vue3vitets进行开发 官网地址: https://x6.antv.antgroup.com/examples/showcase/pra…...
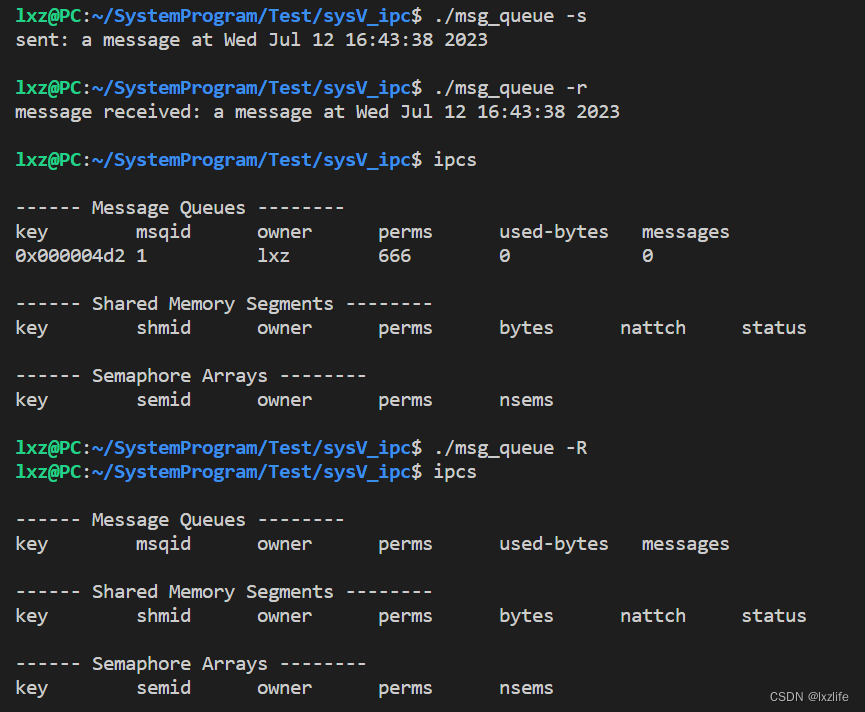
sys V 进程间通信之消息队列
note msgget获取内核消息队列实例 msgctl可以删除内核消息队列实例 msgsnd\msgrcv函数注意struct msgbuf字段的填充 code #include <stdio.h> #include <stdlib.h> #include <string.h> #include <time.h> #include <unistd.h> #include &l…...

Android 报错,闪退(错误)日志保存到手机内存中,以文本文件的形式保存
1.直接贴代码 import android.app.AlarmManager; import android.app.PendingIntent; import android.content.Context; import android.content.Intent; import android.os.Environment; import android.util.Log;import com.nuotu.atmBookClient.App;import java.io.File; i…...

flutter聊天界面-加号【➕】更多展开相机、相册等操作Panel
flutter聊天界面-加号【➕】更多展开相机、相册等操作Panel 在之前实现了flutter聊天界面的自定义表情的展示,这里记录一下更多操作展开的相机、相册等操作功能实现。 一、查看效果 更多操作展开的相机、相册等操作功能实现。 二、代码实现 展开的操作按钮可能比…...

浅析泵站自动化技术的发展趋势
摘要:基于泵站对我国水利及水务事业的重要性,文章以城市供水行业大型泵站为对象,分析了泵站自动化技术 发展现状,结合泵站自动化技术的发展需求,从管控一体化、系统自诊断、运行信息实时化管理等方面展望了泵 站自动化…...
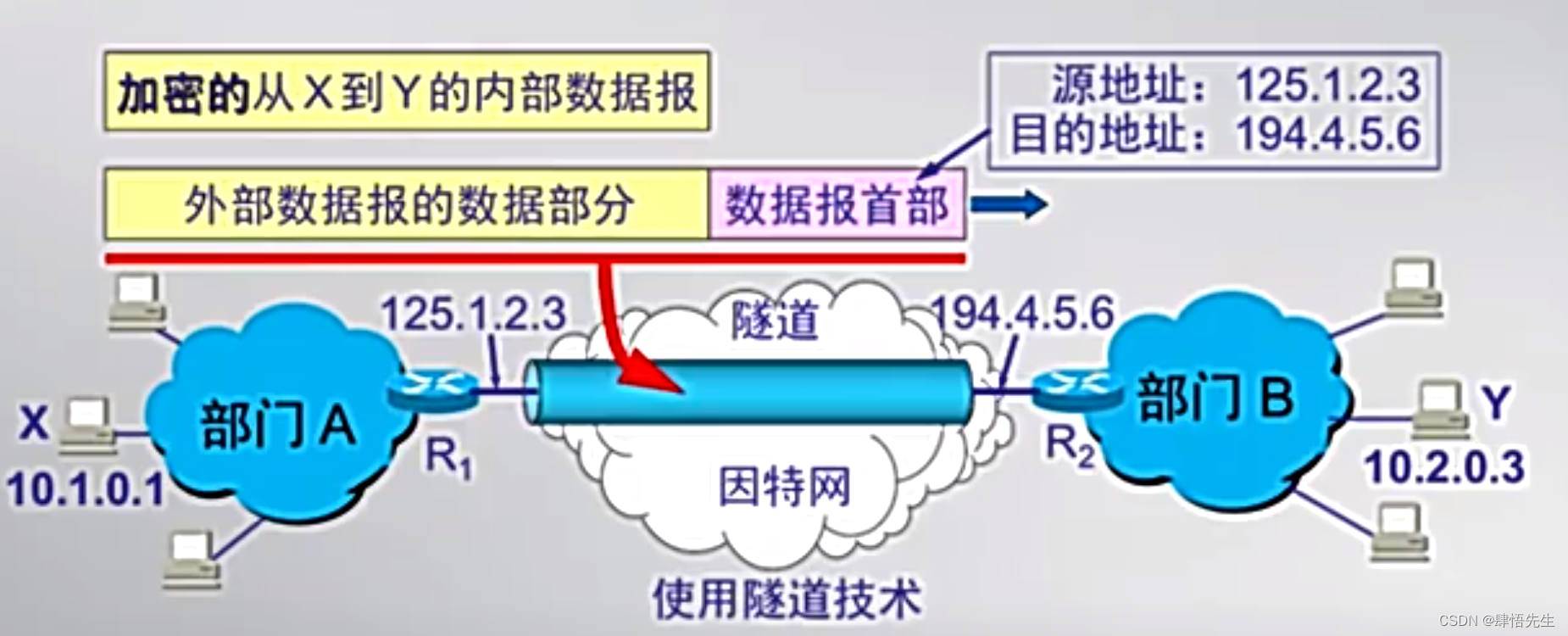
5.4.1 虚拟专用网VPN
5.4.1 虚拟专用网VPN 我们已经学习了因特网的路由协议(5.3.1 因特网的路由协议(一)、5.3.2 因特网的路由协议(二)基于距离向量算法的RIP协议、5.3.3 因特网的路由协议(三)OSPF协议、5.3.4 因特…...

第42节:cesium 火焰效果(含源码+视频)
结果示例: 完整源码: <template><div class="viewer"><!-- :shouldAnimate="true" 添加动画 --><vc-viewer @ready...

MySQL基础篇第5章(排序与分页)
文章目录 1、排序1.1 排序规则1.2 单列排序1.3 多列排序 2、分页2.1 背景2.2 实现规则2.3 拓展 1、排序 1.1 排序规则 使用 ORDER BY 子句排序 ASC(ascend): 升序DESC(descend):降序 ORDER BY 子句在SELECT语句的结尾。 1.2 …...

LeetCode解法汇总2679. 矩阵中的和
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣 描述: 给你一个下标从 0 开始的二维整数数组 nums 。一开始你的分数为 0 。你需要执行…...

flask-apscheduler实现定时任务
秋风阁-北溪入江流 flask-apscheduler是一个支持apscheduler的flask插件,通过flask-apscheduler可以很方便的定义定时任务。 安装flask-apscheduler pip install flask-apschedulerflask-apscheduler组件 apscheduler库包含有组件: triggers…...

FPGA纯verilog实现UDP协议栈,sgmii接口SFP光口收发,提供工程源码和技术支持
目录 1、前言2、我这里已有的UDP方案3、该UDP协议栈性能4、详细设计方案SFPGMII AXIS接口模块AXIS FIFOUDP协议栈1G/2.5G Ethernet PCS/PMA or SGMII 5、vivado工程详解6、上板调试验证并演示准备工作查看ARPUDP数据回环测试 7、福利:工程代码的获取 1、前言 目前网…...

【Python入门系列】第十五篇:Python数据可视化和图表绘制
文章目录 前言一、可视化与绘图常用库二、Matplotlib1、折线图2、散点图3、柱状图: 三、Seaborn1、散点图2、箱线图3、小提琴图4、热力图 四、Plotly1、折线图2、散点图3、条形图 总结 前言 数据可视化是数据分析和数据科学中非常重要的一部分。通过可视化…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
