机器学习与深度学习——自定义函数进行线性回归模型
机器学习与深度学习——自定义函数进行线性回归模型
目的与要求
1、通过自定义函数进行线性回归模型对boston数据集前两个维度的数据进行模型训练并画出SSE和Epoch曲线图,画出真实值和预测值的散点图,最后进行二维和三维度可视化展示数据区域。
2、通过自定义函数进行线性回归模型对boston数据集前四个维度的数据进行模型训练并画出SSE和Epoch曲线图,画出真实值和预测值的散点图,最后进行可视化展示数据区域。
步骤
1、先载入boston数据集 Load Iris data
2、分离训练集和设置测试集split train and test sets
3、对数据进行标准化处理Normalize the data
4、自定义损失函数
5、使用梯度下降算法训练线性回归模型
6、初始化模型参数
7、训练模型
8、对训练集和新数据进行预测
9、画出SSE和Epoch折线图
10、画出真实值和预测值的散点图
11、进行可视化
代码
1、通过自定义函数进行线性回归模型对boston数据集前两个维度的数据进行模型训练并画出SSE和Epoch曲线图,画出真实值和预测值的散点图,最后进行二维和三维度可视化展示数据区域。
#引入所需库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D# 读取数据
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]
x = data[:,:2] # 只使用前两个特征进行线性回归
y = target.reshape(-1,1)#自定义函数进行线性回归
def compute_cost(X, y, theta):"""计算损失函数(平均误差平方和)"""m = len(y)predictions = X.dot(theta)cost = (1/(2*m)) * np.sum(np.square(predictions-y))return costdef gradient_descent(X, y, theta, learning_rate, num_epochs):"""使用梯度下降算法训练线性回归模型"""m = len(y)cost_history = np.zeros(num_epochs)theta_history = np.zeros((num_epochs, theta.shape[0]))for epoch in range(num_epochs):predictions = X.dot(theta)errors = predictions - ytheta = theta - (1/m) * learning_rate * (X.T.dot(errors))cost = compute_cost(X, y, theta)cost_history[epoch] = costtheta_history[epoch,:] = theta.Treturn theta, cost_history, theta_history#对输入特征进行标准化
mean_x = np.mean(x, axis=0) #求出每一列特征的平均值
std_x = np.std(x, axis=0) #求出每一列特征的标准差。
x = (x - mean_x) / std_x #将每一列特征进行标准化,即先将原始数据减去该列的平均值,再除以该列的标准差,这样就能得到均值为0,标准差为1的特征
X = np.hstack([np.ones((len(x),1)), x]) # 添加一列全为1的特征,表示截距项# 初始化模型参数
theta = np.zeros((X.shape[1],1))# 训练模型
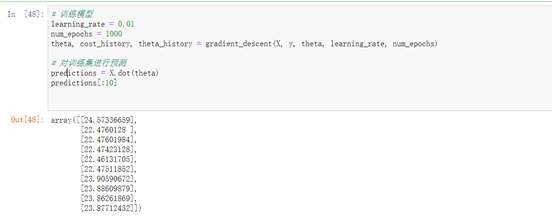
learning_rate = 0.01
num_epochs = 1000
theta, cost_history, theta_history = gradient_descent(X, y, theta, learning_rate, num_epochs)# 对训练集进行预测
predictions = X.dot(theta)
predictions[:10]# 对新数据进行预处理
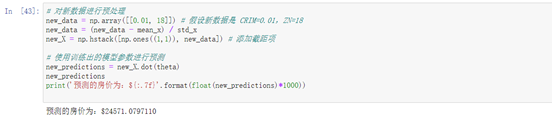
new_data = np.array([[0.01, 18]]) # 假设新数据是 CRIM=0.01,ZN=18
new_data = (new_data - mean_x) / std_x
new_X = np.hstack([np.ones((1,1)), new_data]) # 添加截距项# 使用训练出的模型参数进行预测
new_predictions = new_X.dot(theta)
new_predictions
print('预测的房价为:${:.7f}'.format(float(new_predictions)*1000))# 画出Epoch曲线图
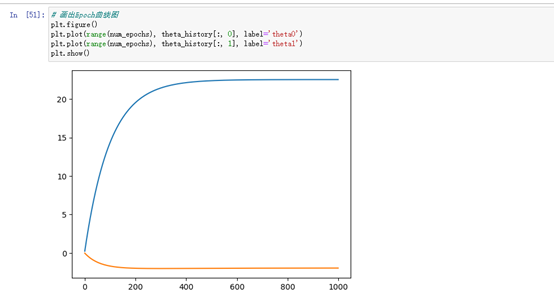
#将每个特征在训练过程中更新的参数θ的变化情况绘制出来,可以看到不同特征在训练过程中的变化趋势
plt.figure()
plt.plot(range(num_epochs), theta_history[:, 0], label='theta0')
plt.plot(range(num_epochs), theta_history[:, 1], label='theta1')
plt.show()# 画出SSE和Epoch折线图
plt.figure(figsize=(10,5))
plt.plot(range(num_epochs), cost_history)
plt.xlabel('Epoch')
plt.ylabel('SSE')
plt.title('SSE vs. Epoch')
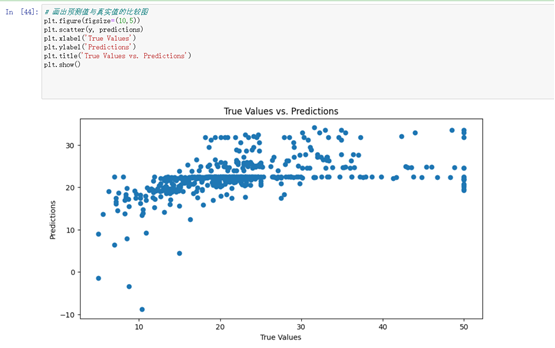
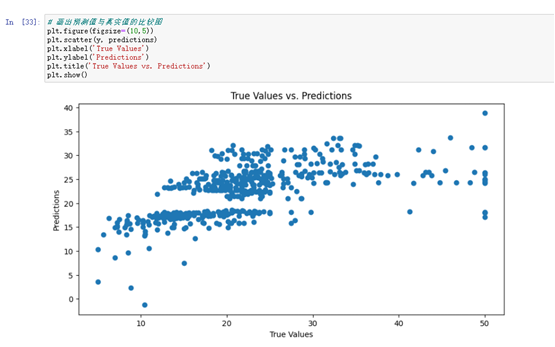
plt.show()# 画出预测值与真实值的比较图
plt.figure(figsize=(10,5))
plt.scatter(y, predictions)
plt.xlabel('True Values')
plt.ylabel('Predictions')
plt.title('True Values vs. Predictions')
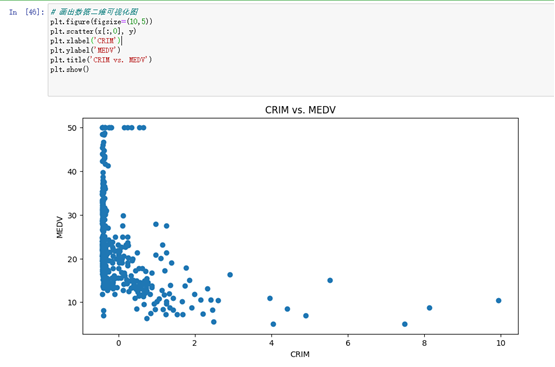
plt.show()# 画出数据二维可视化图
plt.figure(figsize=(10,5))
plt.scatter(x[:,0], y)
plt.xlabel('CRIM')
plt.ylabel('MEDV')
plt.title('CRIM vs. MEDV')
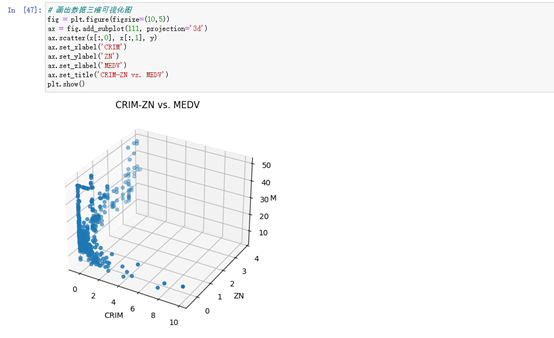
plt.show()# 画出数据三维可视化图
fig = plt.figure(figsize=(10,5))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x[:,0], x[:,1], y)
ax.set_xlabel('CRIM')
ax.set_ylabel('ZN')
ax.set_zlabel('MEDV')
ax.set_title('CRIM-ZN vs. MEDV')
plt.show()1、通过自定义函数进行线性回归模型对boston数据集前四个维度的数据进行模型训练并画出SSE和Epoch曲线图,画出真实值和预测值的散点图,最后进行可视化展示数据区域。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#载入数据
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]
x = data[:,:2]#前2个维度
y = target
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D# 读取数据
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]
x = data[:,:4] #
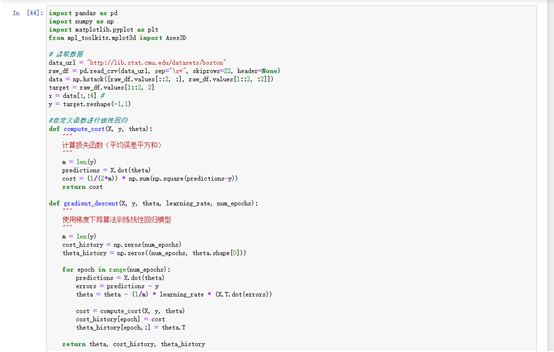
y = target.reshape(-1,1)#自定义函数进行线性回归
def compute_cost(X, y, theta):"""计算损失函数(平均误差平方和)"""m = len(y)predictions = X.dot(theta)cost = (1/(2*m)) * np.sum(np.square(predictions-y))return costdef gradient_descent(X, y, theta, learning_rate, num_epochs):"""使用梯度下降算法训练线性回归模型"""m = len(y)cost_history = np.zeros(num_epochs)theta_history = np.zeros((num_epochs, theta.shape[0]))for epoch in range(num_epochs):predictions = X.dot(theta)errors = predictions - ytheta = theta - (1/m) * learning_rate * (X.T.dot(errors))cost = compute_cost(X, y, theta)cost_history[epoch] = costtheta_history[epoch,:] = theta.Treturn theta, cost_history, theta_history#对输入特征进行标准化
mean_x = np.mean(x, axis=0) #求出每一列特征的平均值
std_x = np.std(x, axis=0) #求出每一列特征的标准差。
x = (x - mean_x) / std_x #将每一列特征进行标准化,即先将原始数据减去该列的平均值,再除以该列的标准差,这样就能得到均值为0,标准差为1的特征
X = np.hstack([np.ones((len(x),1)), x]) # 添加一列全为1的特征,表示截距项# 初始化模型参数
theta = np.zeros((X.shape[1],1))# 训练模型
learning_rate = 0.01
num_epochs = 1000
theta, cost_history, theta_history = gradient_descent(X, y, theta, learning_rate, num_epochs)
# 画出Epoch曲线图
#将每个特征在训练过程中更新的参数θ的变化情况绘制出来,可以看到不同特征在训练过程中的变化趋势
plt.figure()
plt.plot(range(num_epochs), theta_history[:, 0], label='theta0')
plt.plot(range(num_epochs), theta_history[:, 1], label='theta1')
plt.plot(range(num_epochs), theta_history[:, 2], label='theta2')
plt.plot(range(num_epochs), theta_history[:, 3], label='theta3')
plt.show()# 对训练集进行预测
predictions = X.dot(theta)
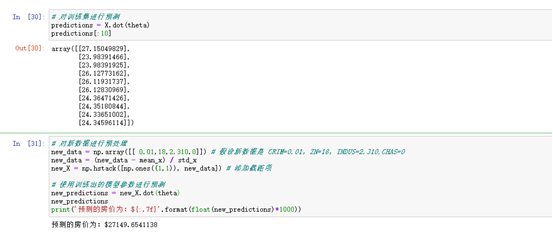
predictions[:10]# 对新数据进行预处理
new_data = np.array([[ 0.01,18,2.310,0]]) # 假设新数据是 CRIM=0.01,ZN=18,INDUS=2.310,CHAS=0
new_data = (new_data - mean_x) / std_x
new_X = np.hstack([np.ones((1,1)), new_data]) # 添加截距项# 使用训练出的模型参数进行预测
new_predictions = new_X.dot(theta)
new_predictions
print('预测的房价为:${:.7f}'.format(float(new_predictions)*1000))
# 画出SSE曲线图
plt.figure()
plt.plot(range(num_epochs), cost_history)
plt.xlabel('Epoch')
plt.ylabel('SSE')
plt.title('SSE vs. Epoch')
plt.show()
# 画出预测值与真实值的比较图
plt.figure(figsize=(10,5))
plt.scatter(y, predictions)
plt.xlabel('True Values')
plt.ylabel('Predictions')
plt.title('True Values vs. Predictions')
plt.show()# 可视化前四个维度的数据
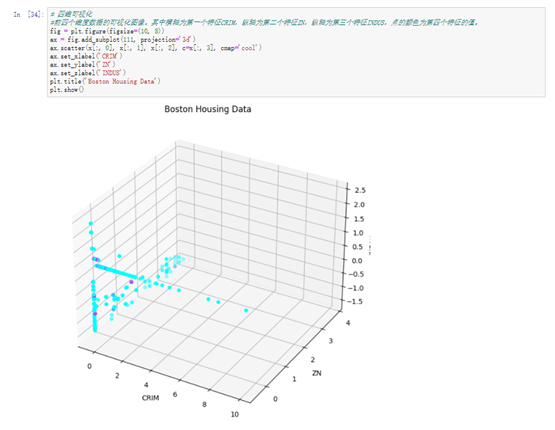
#前四个维度数据的可视化图像。其中横轴为第一个特征CRIM,纵轴为第二个特征ZN,纵轴为第三个特征INDUS,点的颜色为第四个特征的值。
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x[:, 0], x[:, 1], x[:, 2], c=x[:, 3], cmap='cool')
ax.set_xlabel('CRIM')
ax.set_ylabel('ZN')
ax.set_zlabel('INDUS')
plt.title('Boston Housing Data')
plt.show()效果图
1、通过自定义函数进行线性回归模型对boston数据集前两个维度的数据进行模型训练并画出SSE和Epoch曲线图,画出真实值和预测值的散点图,最后进行二维和三维度可视化展示数据区域。

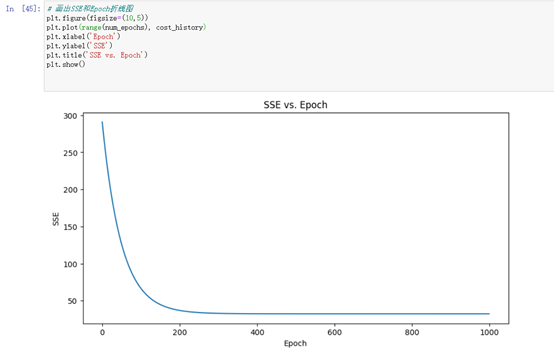
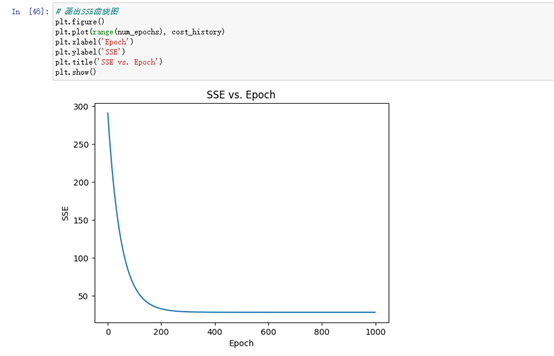
画出SSE(误差平方和)随Epoch(迭代次数)的变化曲线图,用来评估模型训练的效果。在每个Epoch,模型都会计算一次预测值并计算预测值与实际值之间的误差(即损失),然后通过梯度下降算法更新模型参数,使得下一次预测的误差更小。随着Epoch的增加,SSE的值会逐渐减小,直到收敛到一个最小值。
2、通过自定义函数进行线性回归模型对boston数据集前四个维度的数据进行模型训练并画出SSE和Epoch曲线图,画出真实值和预测值的散点图,最后进行可视化展示数据区域。

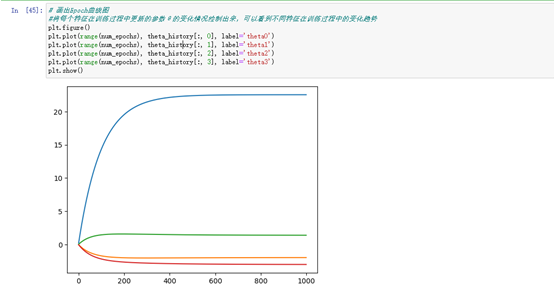
画出SSE(误差平方和)随Epoch(迭代次数)的变化曲线图,用来评估模型训练的效果。在每个Epoch,模型都会计算一次预测值并计算预测值与实际值之间的误差(即损失),然后通过梯度下降算法更新模型参数,使得下一次预测的误差更小。随着Epoch的增加,SSE的值会逐渐减小,直到收敛到一个最小值。
使用梯度下降算法训练线性回归模型的基本思路是:先随机初始化模型参数θ,然后通过迭代调整参数θ,使得损失函数的值尽量小。模型训练完成后,我们可以用训练好的模型对新的数据进行预测。
相关文章:

机器学习与深度学习——自定义函数进行线性回归模型
机器学习与深度学习——自定义函数进行线性回归模型 目的与要求 1、通过自定义函数进行线性回归模型对boston数据集前两个维度的数据进行模型训练并画出SSE和Epoch曲线图,画出真实值和预测值的散点图,最后进行二维和三维度可视化展示数据区域。 2、通过…...

大屏项目也不难
项目环境搭建 使用create-vue初始化项目 npm init vuelatest准备utils模块 业务背景:大屏项目属于后台项目的一个子项目,用户的token是共享的 后台项目 - token - cookie 大屏项目要以同样的方式把token获取到,然后拼接到axios的请求头中…...

c#webclient请求中经常出现的几种异常
WebClient是.NET Framework提供的用于HTTP请求的类,如果在使用WebClient时遇到异常,我们可以根据具体的异常类型进行处理。 以下是一些常见的WebClient异常及其处理方法: System.Net.WebException WebException通常是由于请求超时、网络连…...
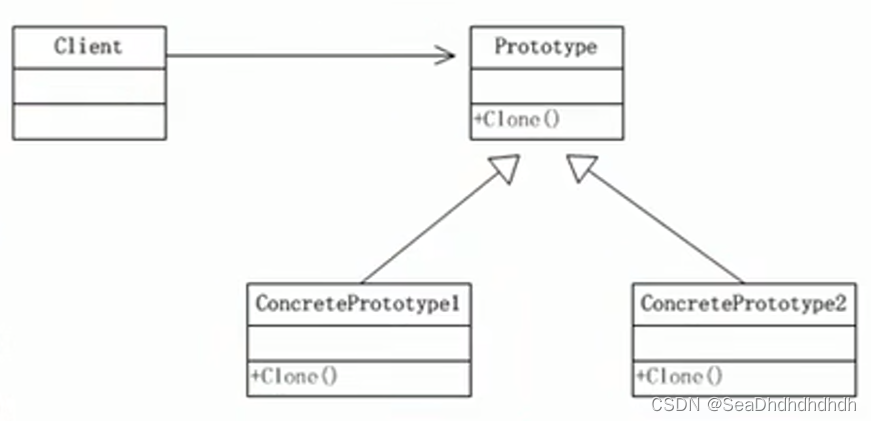
设计模式-原型模式
目录 一、传统方式 二、原型模式 三、浅拷贝和深拷贝 克隆羊问题: 现在有一只羊tom,姓名为: tom,年龄为: 1,颜色为: 白色,请编写程序创建和tom羊属性完全相同的10只羊。 一、传统方式 public class Client {public static vo…...

sentinel介绍-分布式微服务流量控制
官网地址 https://sentinelguard.io/ 介绍 随着微服务的流行,服务和服务之间的稳定性变得越来越重要。Sentinel 是面向分布式、多语言异构化服务架构的流量治理组件,主要以流量为切入点,从流量路由、流量控制、流量整形、熔断降级、系统自…...

基于Redisson的Redis结合布隆过滤器使用
一、场景 缓存穿透问题 一般情况下,先查询Redis缓存,如果Redis中没有,再查询MySQL。当某一时刻访问redis的大量key都在redis中不存在时,所有查询都要访问数据库,造成数据库压力顿时上升,这就是缓存穿透。…...

BrowserRouter刷新404解决方案
1、本地开发环境 在js脚本命令里加上 --history-api-fallback "scripts": {"serve": "webpack serve --config webpack.dev.js --history-api-fallback" }2、生产环境,可以修改 nglnx 配置: server {listen XXXX; //端口号…...
解决appium-doctor报opencv4nodejs cannot be found
一、下载cmake 在CMake官网下载:cmake-3.6.1-win64-x64.msi 二、安装cmake cmake安装过程 在安装时要选择勾选为所有用户添加CMake环境变量 三、检查cmake安装 重新管理员打开dos系统cmd命令提示符,输入cmake -version cmake -version四、安装opencv4no…...

安卓通过adb pull和adb push 手机与电脑之间传输文件
1.可以参考这篇文章 https://www.cnblogs.com/hhddcpp/p/4247923.html2.根据上面的文章,我做了如下修改 //设置/system为可读写: adb remount //复制手机中的文件到电脑中。需要在电脑中新建一个文件夹,我新建的文件夹为ce文件夹 adb pull …...

java常用的lambda表达式总结
一、概述 lambda表达式是JDK8中的一个新特性,对某些匿名内部类进行简化,是函数式编程; 二、基本格式 (参数列表)->{方法体代码} 三、Stream流 是jdk8中的新特性,将数据以流的形式进行操作 三、常用方法解析 3.1、准备工作 …...
分布式应用之zookeeper集群+消息队列Kafka
一、zookeeper集群的相关知识 1.zookeeper的概念 ZooKeeper是一个分布式的,开放源码的分布式应用程序协调服务,是Google的Chubby一个开源的实现,是Hadoop和Hbase的重要组件。它是一个为分布式应用提供一致性服务的软件,提供的功能…...
)
GStreamer学习笔记(四)
Time management 仅当管道处于PLAYING状态时,可以刷新屏幕。如果不在PLAYING状态,什么都不做,因为大多数查询都会失败。 函数与知识点 GstClockTime 说明:所需的超时时间必须以GstClockTime的形式指定。即以纳秒(ns…...
DBeaver连接华为高斯数据库 DBeaver连接Gaussdb数据库 DBeaver connect Gaussdb
DBeaver连接华为高斯数据库 DBeaver连接Gaussdb数据库 DBeaver connect Gaussdb 一、概述 华为GaussDB出来已经有一段时间,最近工作中刚到Gauss数据库。作为coder,那么如何通过可视化工具来操作Gauss呢? 本文将记录使用免费、开源的DBeaver来…...

.net core 2.1 简单部署IIS运行
netcore的项目不像netFramework那么方便部署到iis还是要费点功夫的 比如我想把这个netcore2.1的项目部署到iis并运行: 按照步骤走: 一、确认自己的netcore环境 1、需要安装下面3个环境包(如果电脑已安装请忽略) 检查是否安装cmd命令:cmd&…...

提高视觉检测系统稳定性的隐藏办法——10G高速图像采集卡
提高视觉检测系统稳定性的隐藏办法——10G高速图像采集卡 目前,随着我国各方面配套基础设施建设的完善,企业技术、资金的积累,各行各业积极探索和大胆的尝试机器视觉技术,实现工业自动化、智能化。在机器视觉系统的使用过程中&am…...

注解方式实现数据库字段加密与解密
目录 前言实现步骤定义注解加密工具类定义mybatis拦截器 总结 前言 一些敏感信息存入数据需要进行加密处理,比如电话号码,身份证号码等,从数据库取出到前端展示时需要解密,如果分别在存入取出时去做处理,会很繁锁&…...
C\C++ 使用socket判断ip是否能连通
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan 简介: 使用socket判断ip是否能联通 效果: 代码: #include <iostream> #include <cstdlib> #include <cstdio> #include &…...
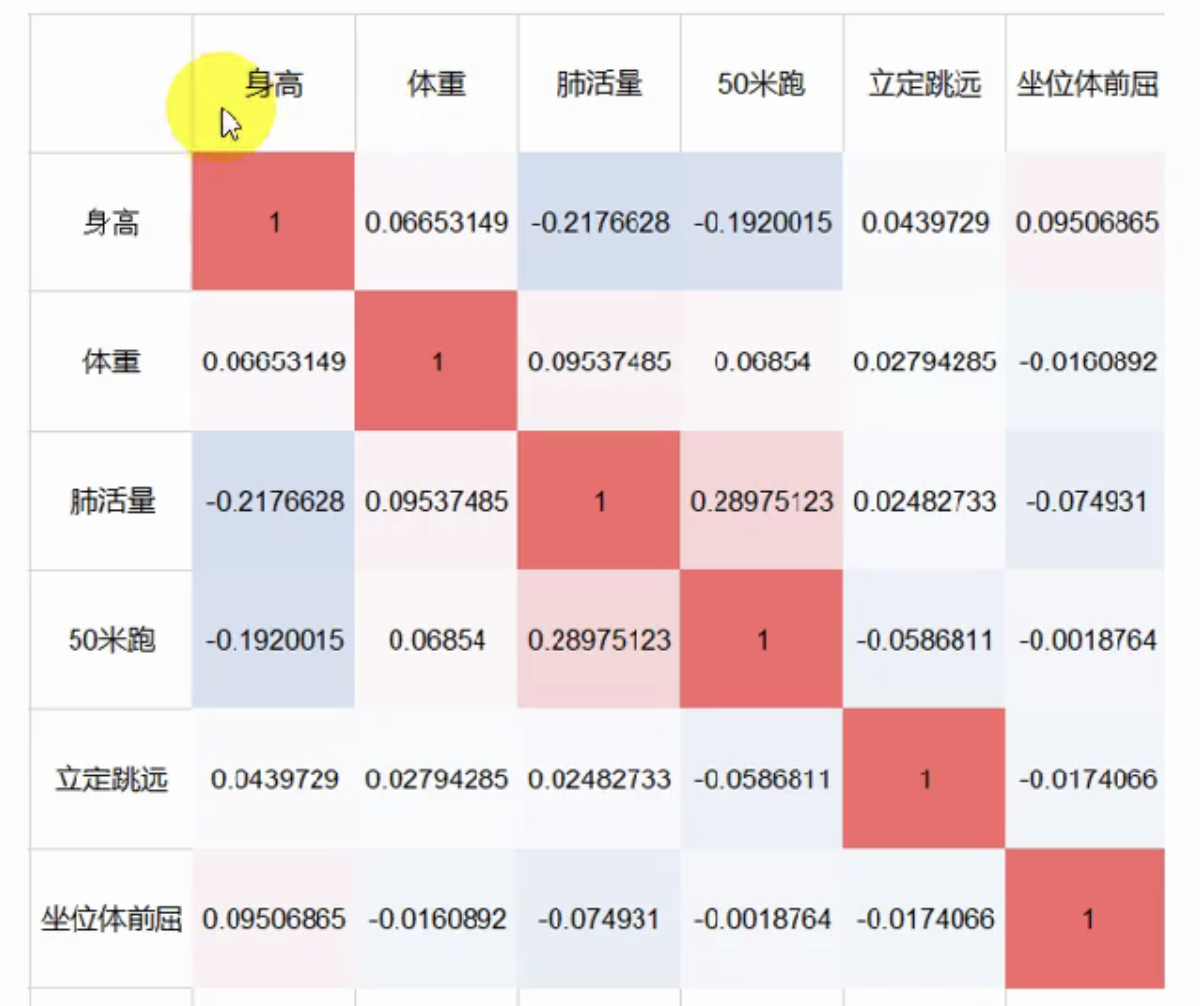
数学建模-相关系数
excel基本操作:ctrl右,ctrl左,ctrlshift下/右,ctrlshift空格 题目里有数据,给出描述性统计是比较好的习惯 excel描述性统计:数据-数据分析-描述统计 MATLAB要做散点图C62个 SPSS可以直接画出两两之间的散…...
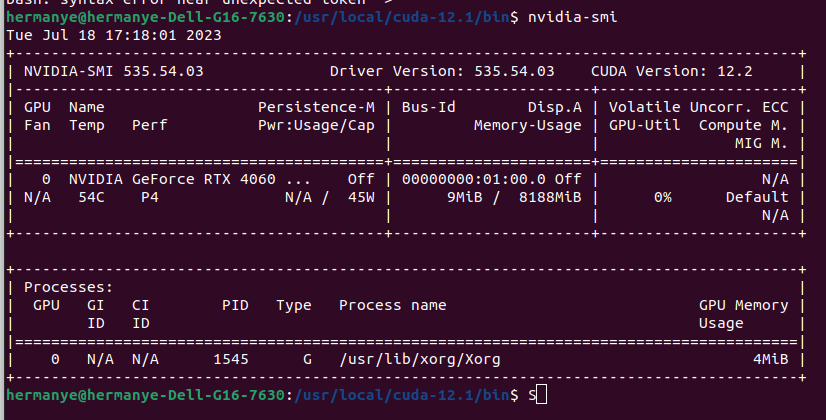
Ubuntu下安装、配置及重装CUDA教程
安装CUDA 前往Nvidia CUDA Tools官网选择对应的架构和版本下载CUDA 以如下架构和版本为例: 查看显卡驱动 nvidia-smi如果显卡驱动已经装了,那么在CUDA安装过程中不用再勾选安装driver 下载并安装CUDA wget https://developer.download.nvidia.co…...

自学网络安全(黑客)为什么火了?
网安专业从始至终都是需要学习的,大学是无法培养出合格的网安人才的。这就是为啥每年网安专业毕业生并不少,而真正从事网安岗位的人,寥寥无几的根本原因。 如果将来打算从事网安岗位,那么不断学习是你唯一的途径。 网络安全为什…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
