23.7.25 杭电暑期多校3部分题解
1005 - Out of Control
题目大意
解题思路
code
1009 - Operation Hope
题意、思路待补
code
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 9;
struct lol {int x, id;} e[3][N * 2];
int t, n, a[3][N * 2], hd[3], tl[3], vis[N * 2], q[N * 2], num, f[N * 2], ans;
bool cmp(lol a, lol b) {return a.x < b.x;}
int getx(int x, int p, int k) {if (hd[k] <= tl[k]) {int y = e[k][hd[k]].x, id = e[k][hd[k]].id;if (y < x - p) {++ hd[k]; return id;}y = e[k][tl[k]].x; id = e[k][tl[k]].id;if (y > x + p) {-- tl[k]; return id;}}return 0;
}
void dfs(int x, int p) {vis[x] = 1;for (int k = 0; k < 3; ++ k) while (1) {int y = getx(a[k][x], p, k);if (!y) break;if (y <= n) if (!vis[y + n]) dfs(y + n, p); else;else if (!vis[y - n]) dfs(y - n, p); else;}q[++ num] = x;
}
void dfs1(int x, int p) {vis[x] = 0; f[x] = ans;for (int k = 0; k < 3; ++ k) while (1) {int y = getx(a[k][x <= n ? x + n : x - n], p, k);if (!y) break;if (vis[y]) dfs1(y, p);}
}
int chk(int p) {num = ans = 0;for (int i = 1; i <= 2 * n; ++ i) vis[i] = 0;for (int k = 0; k < 3; ++ k) hd[k] = 1, tl[k] = 2 * n;for (int k = 0; k < 3; ++ k)for (int i = 1; i <= 2 * n; ++ i)if (!vis[i]) dfs(i, p);for (int k = 0; k < 3; ++ k) hd[k] = 1, tl[k] = 2 * n;for (int k = 0; k < 3; ++ k)for (int i = num; i >= 1; -- i)if (vis[q[i]]) ++ ans, dfs1(q[i], p);for (int i = 1; i <= n; ++ i) if (f[i] == f[i + n]) return 0;return 1;
}
int main() {scanf("%d", &t);while (t --) {scanf("%d", &n);for (int i = 1; i <= n; ++ i) {for (int j = 0; j < 3; ++ j)scanf("%d", &a[j][i]),e[j][i].x = a[j][i],e[j][i].id = i;for (int j = 0; j < 3; ++ j)scanf("%d", &a[j][i + n]),e[j][i + n].x = a[j][i + n],e[j][i + n].id = i + n;}for (int k = 0; k < 3; ++ k)sort(e[k] + 1, e[k] + 2 * n + 1, cmp);int l = 0, r = 1e9;while (l <= r) {int mid = (l + r) >> 1;if (chk(mid)) r = mid - 1;else l = mid + 1;}printf("%d\n", l);}return 0;}
相关文章:

23.7.25 杭电暑期多校3部分题解
1005 - Out of Control 题目大意 解题思路 code 1009 - Operation Hope 题意、思路待补 code #include <bits/stdc.h> using namespace std; const int N 1e5 9; struct lol {int x, id;} e[3][N * 2]; int t, n, a[3][N * 2], hd[3], tl[3], vis[N * 2], q[N * …...

【设计模式——学习笔记】23种设计模式——桥接模式Bridge(原理讲解+应用场景介绍+案例介绍+Java代码实现)
问题引入 现在对不同手机类型的不同品牌实现操作编程(比如:开机、关机、上网,打电话等),如图 【对应类图】 【分析】 扩展性问题(类爆炸),如果我们再增加手机的样式(旋转式),就需要增加各个品牌手机的类,同样如果我们…...
文档翻译软件那么多,哪个能满足你的多语言需求?
想象一下,你手中拿着一份外文文件,上面记录着珍贵的知识和信息,但是语言的障碍让你无法领略其中的内容。而此时,一位翻译大师闪亮登场!他的翻译技巧犹如一把魔法笔,能够将文字的魅力和意境完美传递。无论是…...

MySQL 中NULL和空值的区别
MySQL 中NULL和空值的区别? 简介NULL也就是在字段中存储NULL值,空值也就是字段中存储空字符(’’)。区别 1、空值不占空间,NULL值占空间。当字段不为NULL时,也可以插入空值。 2、当使用 IS NOT NULL 或者 IS NULL 时࿰…...
阿里云容器镜像仓库(ACR)的创建和使用
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

工业的相机与镜头(简单选型)
面阵相机,需要多大的分辨率?多少帧数? 前提条件: 1.被检测的物体大小 2.要求检测的精度是多少 3.物体是否在运动过程中进行检测,速度是多少 线阵相机选择(分辨率、扫描行数) 行频:每秒扫描多少行…...
numpy广播机制介绍
广播 广播机制的意义:广播描述了在算术运算期间NumPy如何处理具有不同形状的数组。受某些约束条件的限制,较小的数组会在较大的数组中“广播”,以便它们具有兼容的形状。 在对两个数组进行操作时,NumPy按元素对它们的形状进行比…...

RocketMQ 5.0 无状态实时性消费详解
作者:绍舒 背景 RocketMQ 5.0 版本引入了 Proxy 模块、无状态 pop 消费机制和 gRPC 协议等创新功能,同时还推出了一种全新的客户端类型:SimpleConsumer。 SimpleConsumer 客户端采用了无状态的 pop 机制,彻底解决了在客户端发布…...
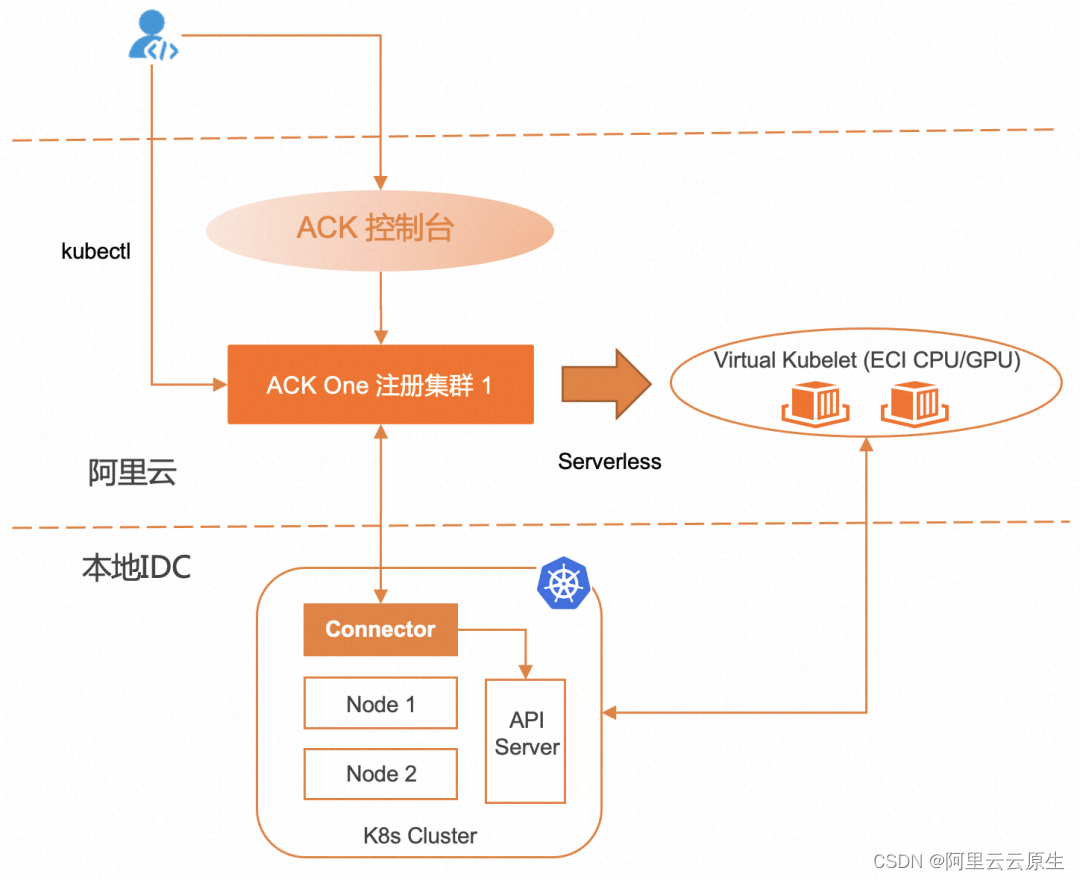
本地 IDC 中的 K8s 集群如何以 Serverless 方式使用云上计算资源
作者:庄宇 在前一篇文章《应对突发流量,如何快速为自建 K8s 添加云上弹性能力》中,我们介绍了如何为 IDC 中 K8s 集群添加云上节点,应对业务流量的增长,通过多级弹性调度,灵活使用云上资源,并通…...
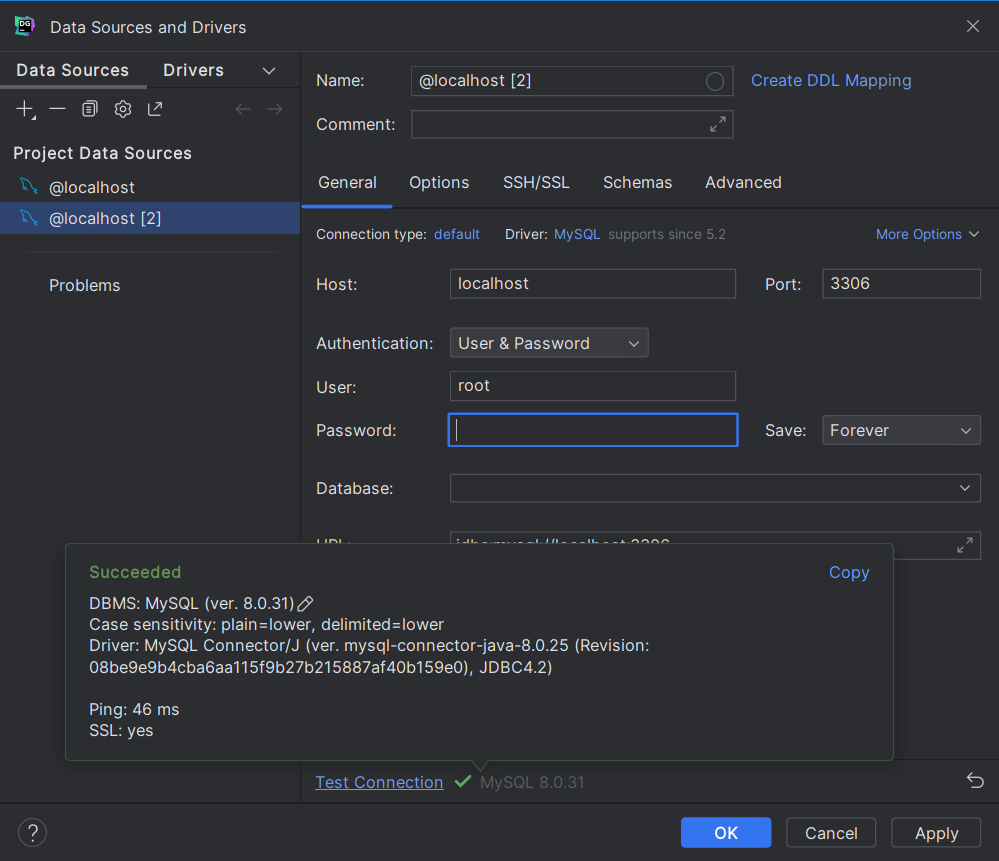
MySQL - 安装、连接、简单介绍
1、安装 MySQL8.0 安装MySQL 8.0的步骤,以 Windows 为例: 1.1 下载MySQL Installer: 需要从MySQL官方网站下载MySQL Installer。在下载页面中,选择适用于Windows的MySQL Installer并下载。 1.2 运行MySQL Installer࿱…...
)
【算法】求欧拉函数(包括完整的证明以及代码模板,建议收藏)
求欧拉函数 前置知识 互质:互质是公约数只有1的两个整数,叫做互质整数。 欧拉函数定义 1 ∼ N − 1 1∼N-1 1∼N−1中与N互质的数的个数被称为欧拉函数,记为 ϕ ( N ) \phi(N) ϕ(N)。 若在算数基本定理中, N p 1 a 1 p 2 a 2 .…...
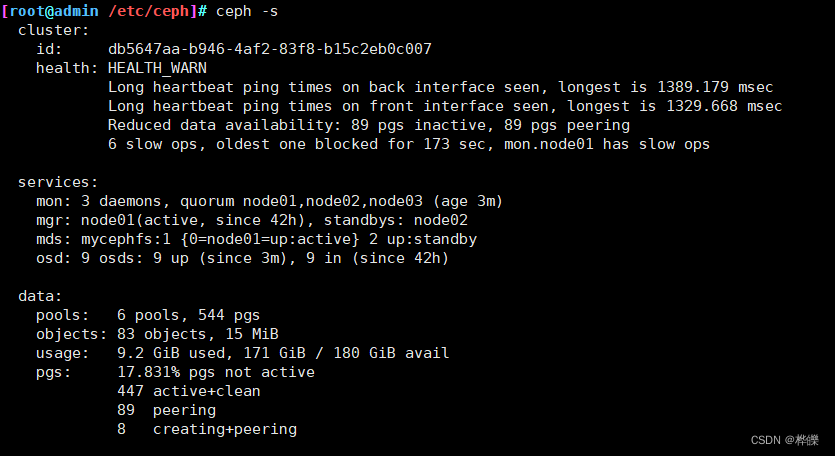
Ceph的应用
文章目录 一、创建 CephFS 文件系统 MDS 接口1)在管理节点创建 mds 服务2)查看各个节点的 mds 服务3)创建存储池,启用 ceph 文件系统4)查看mds状态,一个up,其余两个待命,目前的工作的…...
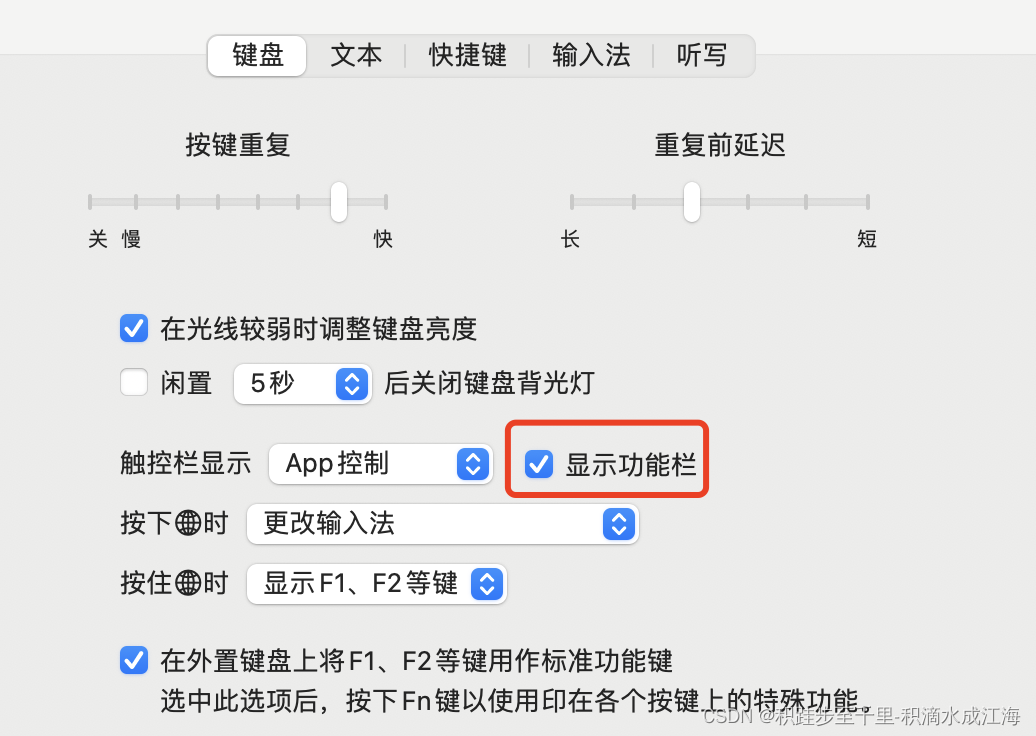
mac m1 触控栏TouchBar功能栏异常
电脑可能在高温下运行时间过长,导致TouchBar之前正常显示的调整屏幕亮度与调整声音等功能的按钮均丢失,然后看了一眼键盘设置,设置也是正常的,已勾选显示功能栏 下面请看 如何在MacBook Pro(macOS Monterey࿰…...

“奢侈品”价格的“快消品”,竹叶青这么想赚年轻人的“茶水钱”?
文 | 螳螂观察 作者 | 青月 或许是受养生焦虑的影响,这届年轻人似乎爱上了喝茶。 《抖音电商茶行业洞察报告》数据显示, 年轻客群已经成为了抖音电商茶行业的增长极,在茶叶、茶具、茶文化书籍等方面,18-30岁消费者是当之无愧消…...
)
【Matlab】基于随机森林算法的时间序列预测(Excel可直接替换数据)
【Matlab】基于随机森林算法的时间序列预测(Excel可直接替换数据) 1.模型原理2.数学公式3.文件结构4.Excel数据5.分块代码6.完整代码7.运行结果1.模型原理 基于随机森林算法的时间序列预测是一种利用随机森林模型来解决时间序列预测问题的方法。在传统的随机森林算法中,对于…...
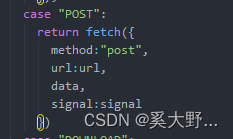
vue 中断请求
1 背景:针对一些请求时间较长,组件销毁后即中断请求; 2 方法: data(){return {//用于取消请求abortController:new AbortController(), } }, created(){//请求接口this.groundAcquisition(); }, beforeDestroy(){//中断请求this.…...

Jwt(Json web token)——从Http协议到session+cookie到Token Jwt介绍 Jwt的应用:登陆验证的流程
目录 引出从Http协议到session&cookie到TokenHTTP协议session & cookiesessioncookie为什么需要session & cookie? JavaEE传统解决长连接方案问题:分布式不适用解决方案:令牌Token Jwt,Json web tokenjwt的结构Header加密算法Ba…...
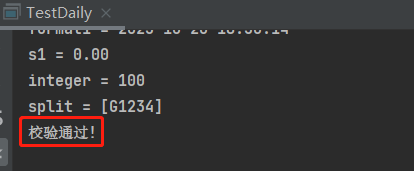
Java使用 java.util.regex.Pattern 正则表达式校验参数值是否规范
场景: java中我们可以利用 Pattern 注解对某个入参进行规则校验,但有些特殊参数在接口入口处不方便校验,需要在代码中校验 一、使用 Pattern 注解校验 Pattern(regexp "^[a-zA-Z0-9]$", message "xxx号限输入字母、…...
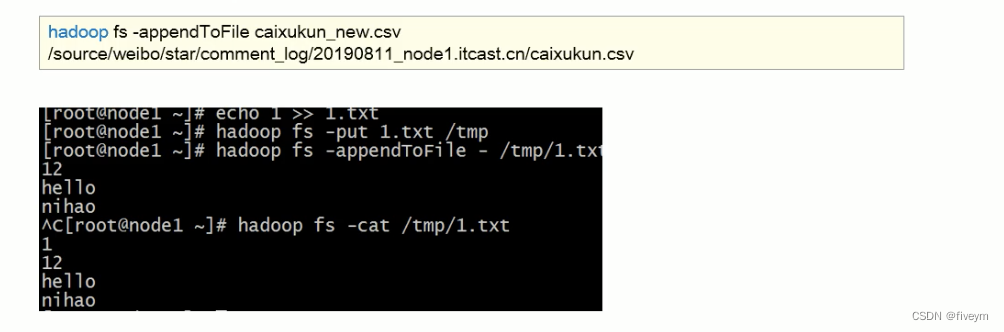
HDFS基本操作命令
这里写目录标题 HDFS Shell CLI客户端说明常用命令hadoop fs -mkdir [-p] <path>hadoop fs -ls [-h] [-R] [<path>...]上传文件到指定目录下方法一:hadoop fs -put [-f] [-p] <localsrc>.....<dst>方法二:hadoop fs -moveFromLocal <loc…...
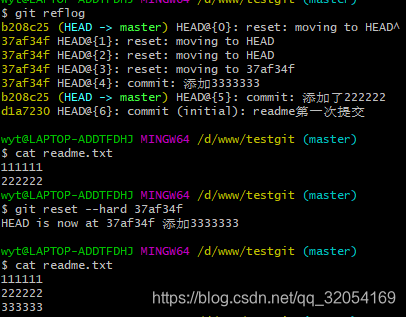
git 实操
首先有安装好的git,安装好后,会在任一目录下右键出现git bash和git gui两个选项 打开git bash,设置好全局变量,用户名和邮箱,设置方法为: git config -- global user.name "xxx" git config --global user.email "xxxxxx.com" 1.创建版本库 git init 命…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
