【算法】求欧拉函数(包括完整的证明以及代码模板,建议收藏)
求欧拉函数
前置知识
互质:互质是公约数只有1的两个整数,叫做互质整数。
欧拉函数定义
1 ∼ N − 1 1∼N-1 1∼N−1中与N互质的数的个数被称为欧拉函数,记为 ϕ ( N ) \phi(N) ϕ(N)。
若在算数基本定理中, N = p 1 a 1 p 2 a 2 . . . p m a m N=p_1^{a_1}p_2^{a_2}...p_m^{a_m} N=p1a1p2a2...pmam,则:
ϕ ( N ) = N ⋅ p 1 − 1 p 1 ⋅ p 2 − 1 p 2 ⋅ . . . ⋅ p m − 1 p m \phi(N)=N\cdot\frac{p_1-1}{p_1}\cdot\frac{p_2-1}{p_2}\cdot...\cdot\frac{p_m-1}{p_m} ϕ(N)=N⋅p1p1−1⋅p2p2−1⋅...⋅pmpm−1
欧拉函数推导
首先我们要知道 1 , 2 , 3... N − 1 , N 1,2,3...N-1,N 1,2,3...N−1,N与 N N N互质的个数是 1 ∼ N 1∼N 1∼N数列去除N的质因子的倍数。
例如 N = 10 , 即 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 N=10,即1,2,3,4,5,6,7,8,9,10 N=10,即1,2,3,4,5,6,7,8,9,10去除 N N N的质因子的倍数 , 则 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 . ,则1,\bcancel{2},3,\bcancel{4},\bcancel{5},\bcancel{6},7,\bcancel{8},9,\bcancel{10}. ,则1,2 ,3,4 ,5 ,6 ,7,8 ,9,10 .
显然, 1 , 3 , 7 , 9 1,3,7,9 1,3,7,9与 10 10 10互质。
由上方结论使用容斥原理进行数学推导如下:
∵ N = p 1 a 1 p 2 a 2 . . . p m a m \because N=p_1^{a_1}p_2^{a_2}...p_m^{a_m} ∵N=p1a1p2a2...pmam
①.从1~n中去掉 p 1 , p 2 , . . . , p k p_1,p_2,...,p_k p1,p2,...,pk的所有倍数的个数,即
n ← n − n p 1 − n p 2 − . . . − n p k n←n-\frac{n}{p_1}-\frac{n}{p_2}-...-\frac{n}{p_k} n←n−p1n−p2n−...−pkn
②.由容斥原理, p i ⋅ p j p_i \cdot p_j pi⋅pj的倍数个数被①减了两次,所以加上所有 p i ⋅ p j p_i\cdot p_j pi⋅pj的倍数的个数(其中 p i , p j p_i,p_j pi,pj是 p 1 ∼ p k p_1∼p_k p1∼pk的排列),即
n ← n + n p 1 ⋅ p 2 + n p 1 ⋅ p 3 + . . . + n p k − 1 ⋅ p k n←n+\frac{n}{p_1\cdot p_2}+\frac{n}{p_1\cdot p_3}+...+\frac{n}{p_{k-1}\cdot p_k} n←n+p1⋅p2n+p1⋅p3n+...+pk−1⋅pkn
③.减去所有 p i ⋅ p j ⋅ p k p_i\cdot p_j \cdot p_k pi⋅pj⋅pk的倍数个数,即
n ← n − n p 1 ⋅ p 2 ⋅ p 3 − n p 1 ⋅ p 2 ⋅ p 4 − . . . − n p k − 2 ⋅ p k − 1 ⋅ p k n←n-\frac{n}{p_1\cdot p_2\cdot p_3}-\frac{n}{p_1\cdot p_2 \cdot p_4}-...-\frac{n}{p_{k-2}\cdot p_{k-1}\cdot p_k} n←n−p1⋅p2⋅p3n−p1⋅p2⋅p4n−...−pk−2⋅pk−1⋅pkn
④.同理,加上所有 p i ⋅ p j ⋅ p k ⋅ p l p_i\cdot p_j \cdot p_k \cdot p_l pi⋅pj⋅pk⋅pl的倍数个数,即
n ← n + n p 1 ⋅ p 2 ⋅ p 3 ⋅ p 4 + n p 1 ⋅ p 2 ⋅ p 3 ⋅ p 5 + . . . + n p k − 3 ⋅ p k − 2 ⋅ p k − 1 ⋅ p k n←n+\frac{n}{p_1\cdot p_2\cdot p_3\cdot p_4}+\frac{n}{p_1\cdot p_2 \cdot p_3\cdot p_5}+...+\frac{n}{p_{k-3}\cdot p_{k-2}\cdot p_{k-1}\cdot {p_k}} n←n+p1⋅p2⋅p3⋅p4n+p1⋅p2⋅p3⋅p5n+...+pk−3⋅pk−2⋅pk−1⋅pkn
KaTeX parse error: Can't use function '\mathord' in text mode at position 1: \̲m̲a̲t̲h̲o̲r̲d̲{\varvdots\rule…
因此,
ϕ ( n ) = n − n p 1 − n p 2 − . . . − n p k + n p 1 ⋅ p 2 + n p 1 ⋅ p 3 + . . . + n p k − 1 ⋅ p k − n p 1 ⋅ p 2 ⋅ p 3 − n p 1 ⋅ p 2 ⋅ p 4 − . . . − n p k − 2 ⋅ p k − 1 ⋅ p k + n p 1 ⋅ p 2 ⋅ p 3 ⋅ p 4 + n p 1 ⋅ p 2 ⋅ p 3 ⋅ p 5 + . . . + n p k − 3 ⋅ p k − 2 ⋅ p k − 1 ⋅ p k − . . . \phi(n)=n-\frac{n}{p_1}-\frac{n}{p_2}-...-\frac{n}{p_k}\\ +\frac{n}{p_1\cdot p_2}+\frac{n}{p_1\cdot p_3}+...+\frac{n}{p_{k-1}\cdot p_k}\\ -\frac{n}{p_1\cdot p_2\cdot p_3}-\frac{n}{p_1\cdot p_2 \cdot p_4}-...-\frac{n}{p_{k-2}\cdot p_{k-1}\cdot p_k}\\ +\frac{n}{p_1\cdot p_2\cdot p_3\cdot p_4}+\frac{n}{p_1\cdot p_2 \cdot p_3\cdot p_5}+...+\frac{n}{p_{k-3}\cdot p_{k-2}\cdot p_{k-1}\cdot {p_k}}\\ -... ϕ(n)=n−p1n−p2n−...−pkn+p1⋅p2n+p1⋅p3n+...+pk−1⋅pkn−p1⋅p2⋅p3n−p1⋅p2⋅p4n−...−pk−2⋅pk−1⋅pkn+p1⋅p2⋅p3⋅p4n+p1⋅p2⋅p3⋅p5n+...+pk−3⋅pk−2⋅pk−1⋅pkn−...
也就是n减去奇数个质因子的倍数个数,加上偶数个质因子的倍数个数,循环往复。将上式等价变形,得到
ϕ ( n ) = n ⋅ ( 1 − 1 p 1 ) ⋅ ( 1 − 1 p 2 ) . . . ⋅ ( 1 − 1 p k ) \phi(n)=n\cdot(1-\frac{1}{p_1})\cdot(1-\frac{1}{p_2})...\cdot(1-\frac{1}{p_k}) ϕ(n)=n⋅(1−p11)⋅(1−p21)...⋅(1−pk1)
证必。
代码模板
int phi(int x)
{int res = x;for (int i = 2; i <= x / i; i ++ )if (x % i == 0){res = res / i * (i - 1);while (x % i == 0) x /= i;}if (x > 1) res = res / x * (x - 1);return res;
}
相关文章:
)
【算法】求欧拉函数(包括完整的证明以及代码模板,建议收藏)
求欧拉函数 前置知识 互质:互质是公约数只有1的两个整数,叫做互质整数。 欧拉函数定义 1 ∼ N − 1 1∼N-1 1∼N−1中与N互质的数的个数被称为欧拉函数,记为 ϕ ( N ) \phi(N) ϕ(N)。 若在算数基本定理中, N p 1 a 1 p 2 a 2 .…...
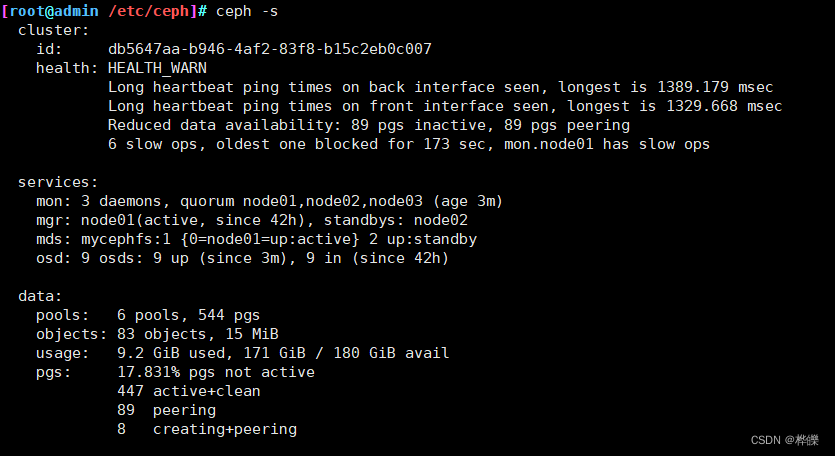
Ceph的应用
文章目录 一、创建 CephFS 文件系统 MDS 接口1)在管理节点创建 mds 服务2)查看各个节点的 mds 服务3)创建存储池,启用 ceph 文件系统4)查看mds状态,一个up,其余两个待命,目前的工作的…...
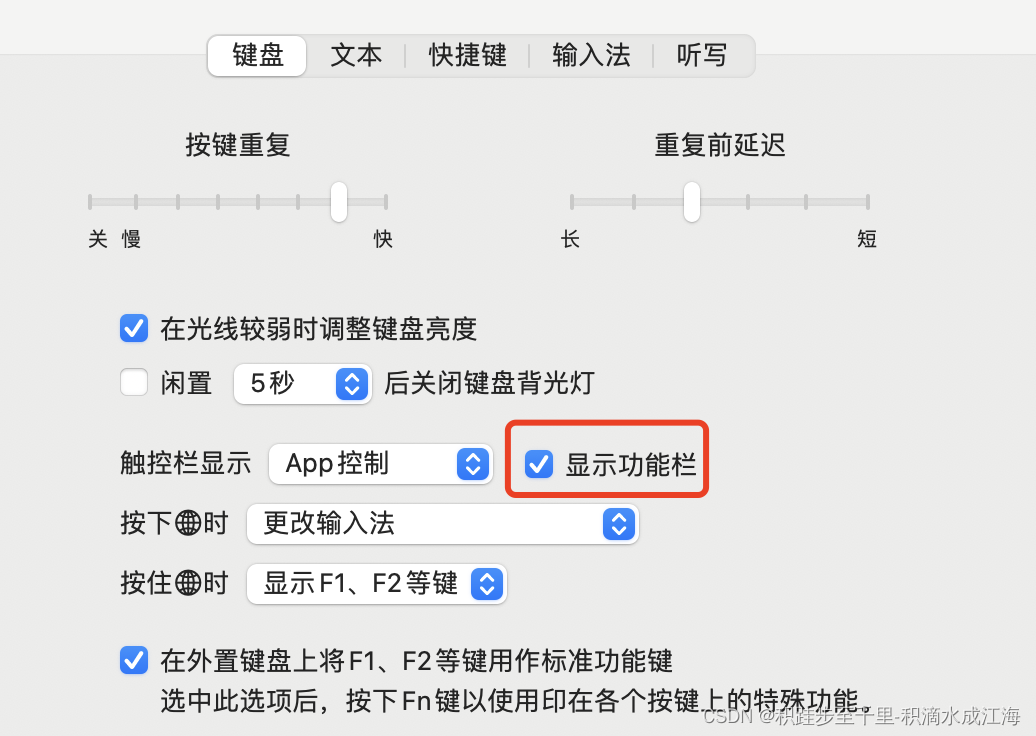
mac m1 触控栏TouchBar功能栏异常
电脑可能在高温下运行时间过长,导致TouchBar之前正常显示的调整屏幕亮度与调整声音等功能的按钮均丢失,然后看了一眼键盘设置,设置也是正常的,已勾选显示功能栏 下面请看 如何在MacBook Pro(macOS Monterey࿰…...

“奢侈品”价格的“快消品”,竹叶青这么想赚年轻人的“茶水钱”?
文 | 螳螂观察 作者 | 青月 或许是受养生焦虑的影响,这届年轻人似乎爱上了喝茶。 《抖音电商茶行业洞察报告》数据显示, 年轻客群已经成为了抖音电商茶行业的增长极,在茶叶、茶具、茶文化书籍等方面,18-30岁消费者是当之无愧消…...
)
【Matlab】基于随机森林算法的时间序列预测(Excel可直接替换数据)
【Matlab】基于随机森林算法的时间序列预测(Excel可直接替换数据) 1.模型原理2.数学公式3.文件结构4.Excel数据5.分块代码6.完整代码7.运行结果1.模型原理 基于随机森林算法的时间序列预测是一种利用随机森林模型来解决时间序列预测问题的方法。在传统的随机森林算法中,对于…...
vue 中断请求
1 背景:针对一些请求时间较长,组件销毁后即中断请求; 2 方法: data(){return {//用于取消请求abortController:new AbortController(), } }, created(){//请求接口this.groundAcquisition(); }, beforeDestroy(){//中断请求this.…...

Jwt(Json web token)——从Http协议到session+cookie到Token Jwt介绍 Jwt的应用:登陆验证的流程
目录 引出从Http协议到session&cookie到TokenHTTP协议session & cookiesessioncookie为什么需要session & cookie? JavaEE传统解决长连接方案问题:分布式不适用解决方案:令牌Token Jwt,Json web tokenjwt的结构Header加密算法Ba…...
Java使用 java.util.regex.Pattern 正则表达式校验参数值是否规范
场景: java中我们可以利用 Pattern 注解对某个入参进行规则校验,但有些特殊参数在接口入口处不方便校验,需要在代码中校验 一、使用 Pattern 注解校验 Pattern(regexp "^[a-zA-Z0-9]$", message "xxx号限输入字母、…...
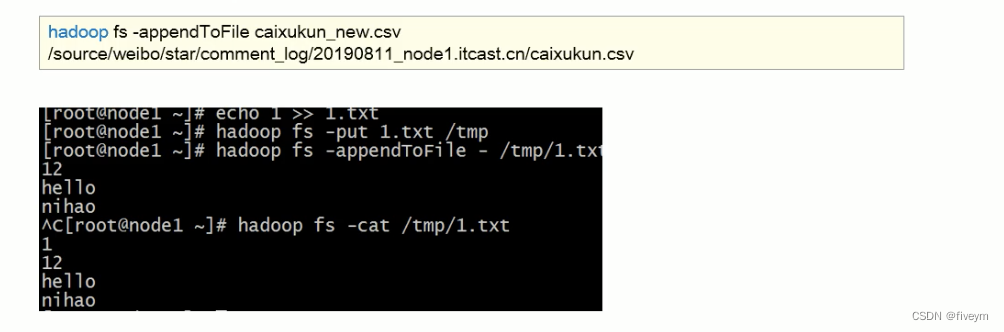
HDFS基本操作命令
这里写目录标题 HDFS Shell CLI客户端说明常用命令hadoop fs -mkdir [-p] <path>hadoop fs -ls [-h] [-R] [<path>...]上传文件到指定目录下方法一:hadoop fs -put [-f] [-p] <localsrc>.....<dst>方法二:hadoop fs -moveFromLocal <loc…...
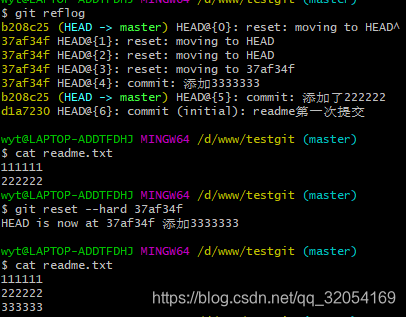
git 实操
首先有安装好的git,安装好后,会在任一目录下右键出现git bash和git gui两个选项 打开git bash,设置好全局变量,用户名和邮箱,设置方法为: git config -- global user.name "xxx" git config --global user.email "xxxxxx.com" 1.创建版本库 git init 命…...
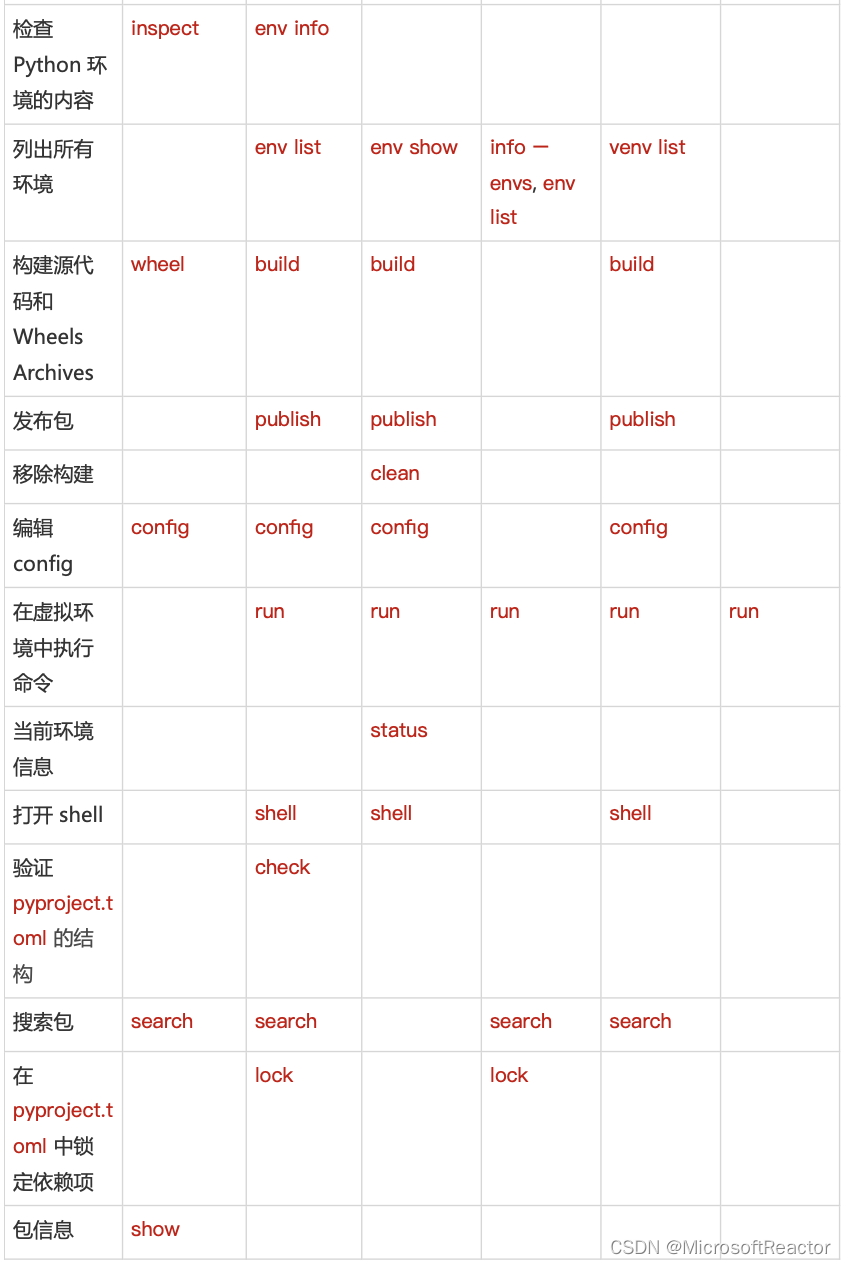
Visual Studio Code Python 扩展中的包管理
排版:Alan Wang Python 凭借其简单的语法和强大的库,目前已成为最流行的编程语言之一,也是最适合那些刚接触编程的人们的语言。但是,随着项目复杂性和规模的增长,管理依赖项的复杂性也会增加。当新用户不断承接更成熟的…...

spring学习笔记九
数据源对象管理 1、加入pom坐标 <dependency><groupId>com.alibaba</groupId><artifactId>druid</artifactId><version>1.1.16</version></dependency><!-- https://mvnrepository.com/artifact/c3p0/c3p0 --><depe…...

java list stream 使用
1、实现List对象集合的简单去重(distinct()) List<User> list list.stream().distinct().collect(Collectors.toList()); 2、实现List集合的根据属性(name)去重 list list.stream().filter(o -> o.getName() ! …...

两个Ubuntu电脑用SSH远程连接
两个Ubuntu电脑用SSH远程连接 1.ssh客户端及服务端的安装: 打开终端后,只需要以下两个命令即可 sudo apt-get install openssh-clientsudo apt-get install openssh-server2.启动ssh服务,执行以下命令: sudo /etc/init.d/ssh …...

讲解 @ServletComponentScan注解
目录: 1、用法介绍2、实例讲解 1、介绍 在SpringBoot项目启动器中添加ServletComponentScan注解后,SpringBoot在启动时会扫描并注册所有带有WebServlet(控制器)、WebFilter(过滤器)、WebListener(监听器&a…...

20款奔驰S350商务型加装原厂前排座椅通风系统,夏天必备的功能
通风座椅的主动通风功能可以迅速将座椅表面温度降至适宜程度,从而确保最佳座椅舒适性。该功能启用后,车内空气透过打孔皮饰座套被吸入座椅内部,持续时间为 8 分钟。然后,风扇会自动改变旋转方向,将更凉爽的环境空气从座…...

Rust vs Go:常用语法对比(十一)
题目来自 Rust Vs Go: Which Language Is Better For Developing High-Performance Applications?[1] 202. Sum of squares Calculate the sum of squares s of data, an array of floating point values. 计算平方和 package mainimport ( "math")func main() { da…...
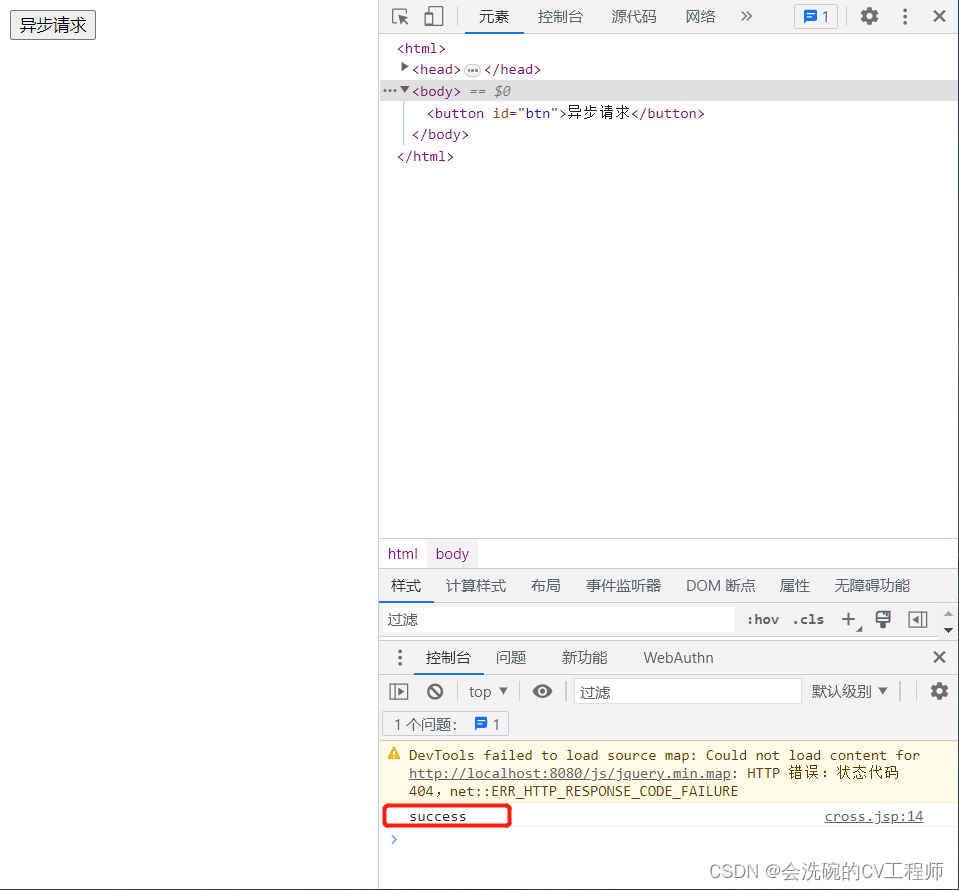
Spring MVC拦截器和跨域请求
一、拦截器简介 SpringMVC的拦截器(Interceptor)也是AOP思想的一种实现方式。它与Servlet的过滤器(Filter)功能类似,主要用于拦截用户的请求并做相应的处理,通常应用在权限验证、记录请求信息的日志、判断用…...

C++初阶--C++入门
目录 前言C关键字命名空间命名空间的定义命名空间的使用加命名空间名称及作用域限定符使用using namespace 命名空间名称引入使用using将命名空间中的成员引入 C的输入与输出缺省参数全缺省半缺省参数 函数重载参数类型不同参数个数不同参数类型顺序不同 引用引用特性 常引用使…...
)
Matlab实现PID控制仿真(附上30个完整仿真源码+数据)
本文介绍了如何使用Matlab实现PID控制器的仿真。首先,我们将简要介绍PID控制器的原理和控制算法。然后,我们将使用Matlab编写一个简单的PID控制器,并使用仿真环境来验证其性能。最后,我们将通过调整PID控制器的参数来优化控制系统…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
