2023“钉耙编程”中国大学生算法设计超级联赛(3)8-bit Zoom
2023“钉耙编程”中国大学生算法设计超级联赛(3)8-bit Zoom
题解
有一张尺寸为 n × n n\times n n×n的图片,你要将图片放大成大小为 n Z 100 × n Z 100 \dfrac{nZ}{100}\times \dfrac{nZ}{100} 100nZ×100nZ的图片。
当下列任何一个条件不成立时,图片不能放大成上述的图片:
- n Z 100 \dfrac{nZ}{100} 100nZ不是整数
- 在放大的图片中,无法确定某些像素的颜色
给出图片,求能否放大成上述的图片。如果可以的话,输出放大后的图片;否则,输出 error \text{error} error。
有 T T T组数据。
1 ≤ T ≤ 10 , 1 ≤ n ≤ 50 , 100 ≤ Z ≤ 200 , Z % 25 = 0 1\leq T\leq 10,1\leq n\leq 50,100\leq Z\leq 200,Z\% 25=0 1≤T≤10,1≤n≤50,100≤Z≤200,Z%25=0
题解
先判断 n Z 100 \dfrac{nZ}{100} 100nZ是不是整数,不是的话输出 error \text{error} error。
先将图放大 Z 25 \dfrac{Z}{25} 25Z倍,这样的话,原图的每个 1 × 1 1\times 1 1×1的格子在放大后的图中变为 Z 25 × Z 25 \dfrac{Z}{25}\times \dfrac{Z}{25} 25Z×25Z的格子。
然后,将图片缩到原来的 1 4 \dfrac 14 41,将每个 4 × 4 4\times 4 4×4的部分变为一个格子。如果出现一个 4 × 4 4\times 4 4×4的部分存在两个像素的颜色不相同的情况,则不合法,输出 error \text{error} error。
放大 Z 25 \dfrac{Z}{25} 25Z倍后再缩到原来的 1 4 \dfrac 14 41,也就是将原图放大 Z 100 \dfrac{Z}{100} 100Z倍,符合题意。如果经过放大在缩小后的图合法,则将最后的图输出即可。
时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
code
#include<bits/stdc++.h>
using namespace std;
int t,n,Z,w,fl;
char a[105][105],b[505][505];
char gt(){char ch=getchar();while(ch<'a'||ch>'z') ch=getchar();return ch;
}
int main()
{scanf("%d",&t);while(t--){scanf("%d%d",&n,&Z);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){a[i][j]=gt();}}if(n*Z%100!=0){printf("error\n");continue;}w=Z/25;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){for(int k=(i-1)*w+1;k<=i*w;k++){for(int l=(j-1)*w+1;l<=j*w;l++){b[k][l]=a[i][j];}}}}fl=0;for(int i=1;i<=n*w;i+=4){for(int j=1;j<=n*w;j+=4){for(int k=0;k<4;k++){for(int l=0;l<4;l++){if(b[i+k][j+l]!=b[i][j]) fl=1;}}}}if(fl) printf("error\n");else{for(int i=1;i<=n*w;i+=4){for(int j=1;j<=n*w;j+=4){printf("%c",b[i][j]);}printf("\n");}}}return 0;
}
相关文章:
8-bit Zoom)
2023“钉耙编程”中国大学生算法设计超级联赛(3)8-bit Zoom
2023“钉耙编程”中国大学生算法设计超级联赛(3)8-bit Zoom 题解 有一张尺寸为 n n n\times n nn的图片,你要将图片放大成大小为 n Z 100 n Z 100 \dfrac{nZ}{100}\times \dfrac{nZ}{100} 100nZ100nZ的图片。 当下列任何一个条件不成…...
【PWN · ret2text | 伪rand()】[HDCTF 2023]pwnner
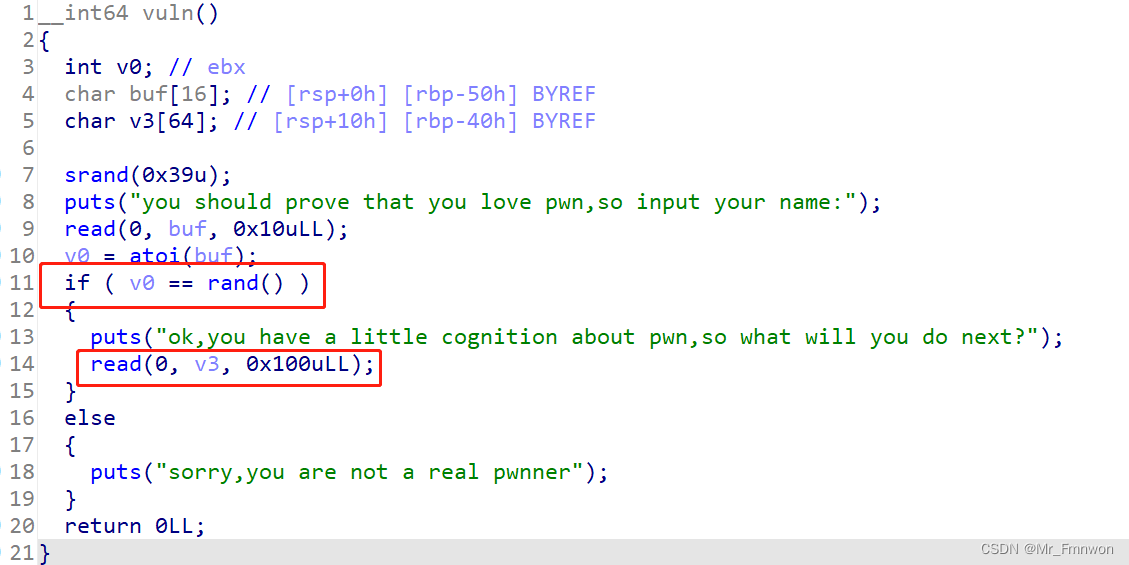
伪随机数以及ctypes库的初步接触 目录 前言 一、题目 二、解题思路 三、exp 总结 前言 一道简单的ret2text,加上一些伪随机的知识,对于本蒟蒻萌新来说,比较新,值得记录。 一、题目 栈溢出保护、PIE保护都没有开。反汇编后…...
第五章:通过对抗擦除的目标区域挖掘:一种简单的语义分割方法
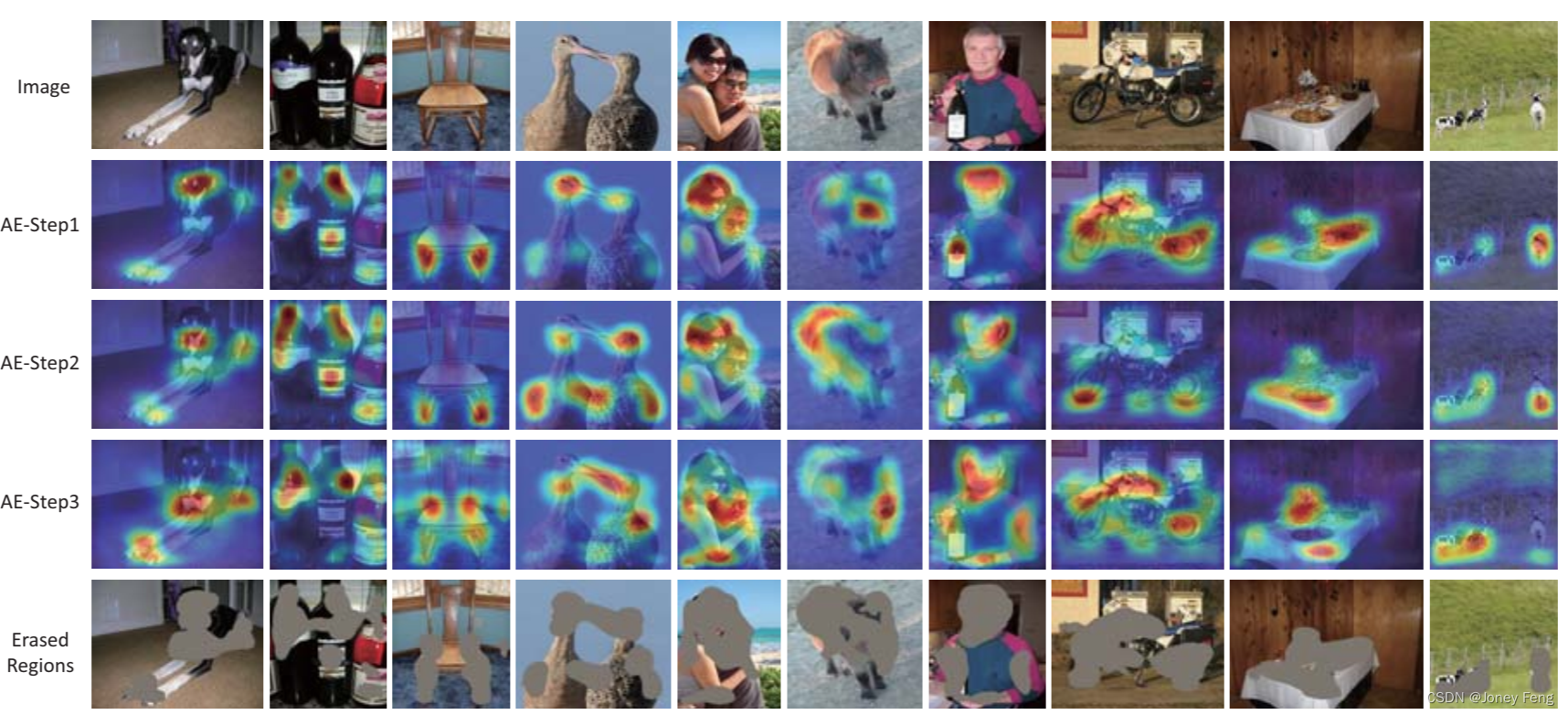
0.摘要 我们研究了一种逐步挖掘具有鉴别性的物体区域的原则方法,使用分类网络来解决弱监督语义分割问题。分类网络只对感兴趣对象中的小而稀疏的鉴别性区域有响应,这与分割任务的要求相背离,分割任务需要定位密集、内部和完整的区域以进行像素…...

自定义view - 玩转字体变色
自定义View步骤: 1>:values__attrs.xml,定义自定义属性; 2>:在第三个构造方法中获取自定义属性; 3>:onMeasure【不是必须的】; 4>:onDraw:绘制代…...

工业边缘网关HiWoo Box的4G/5G CPE功能:为现场无线设备提供网络
引言 随着工业物联网的快速发展,现场设备的无线连接需求越来越迫切。然而,在一些室外或者不方便布网的场景下,为现场的无线设备提供网络仍然是一个挑战。为了满足这一需求,工业边缘网关HiWoo Box引入了4G/5G CPE(Cust…...

Set 和 Map 数据结构
数据结构Set ES6提供了新的数据结构Set。它类似于数组,但是成员的值都是唯一的,没有重复的值。 Set本身是一个构造函数,用来生成Set数据结构。 // 数组去重 const set new Set([1, 2, 3, 4, 4]); [...set] // [1, 2, 3, 4]目前个人感觉Se…...

nginx根据url参数动态代理
nginx根据url参数动态代理 请求url格式,其中参数proxy后面的url就是需要访问的真实地址: http://localhost:9388/?proxyhttp://localhost:8038/Content/layui/font/iconfont.woff?v256 http://localhost:9388/?proxyhttp://localhost:8072/article/A…...
)
TCP协议(收集和记录)
收集写的比较好的文章 TCP四次挥手详解 四次挥手介绍的非常详细, 重点介绍了各种异常情况下协议是如何处理的, 异常处理可以做到两点: 让连接保活, 也许只是一次连接异常让连接死掉后不影响后续的操作, 重点介绍了TIME_WAIT...

【Kafka】自动提交偏移量和手动提交偏移量的区别
区别 自动提交偏移量(Auto Commit Offset)和手动提交偏移量(Manual Commit Offset)是两种不同的消费者偏移量管理方式。 自动提交偏移量: 在自动提交模式下,消费者会定期自动将已消费的消息偏移量提交给…...

缠论线段的划分
第一种情况: 第二种情况: 第二种情况中的特例: 第二种情况的特例: 顶分型成立: 向上线段延续: 顶分型后面底分型,形成三段 插入一个分型的反面例子: dd...

【Linux】Ubuntu基本使用与配置, 以及常见问题汇总(一)
前言 大学期间,感觉很多时候学习课外知识都是被推着往前走,很多内容并没有深入去学习,知识的记录受限于所学比较片面,如今渐渐意识到似乎并没有建立起相关知识的体系架构,缺乏一个系统学习并整理的过程。本文将以Ubunt…...
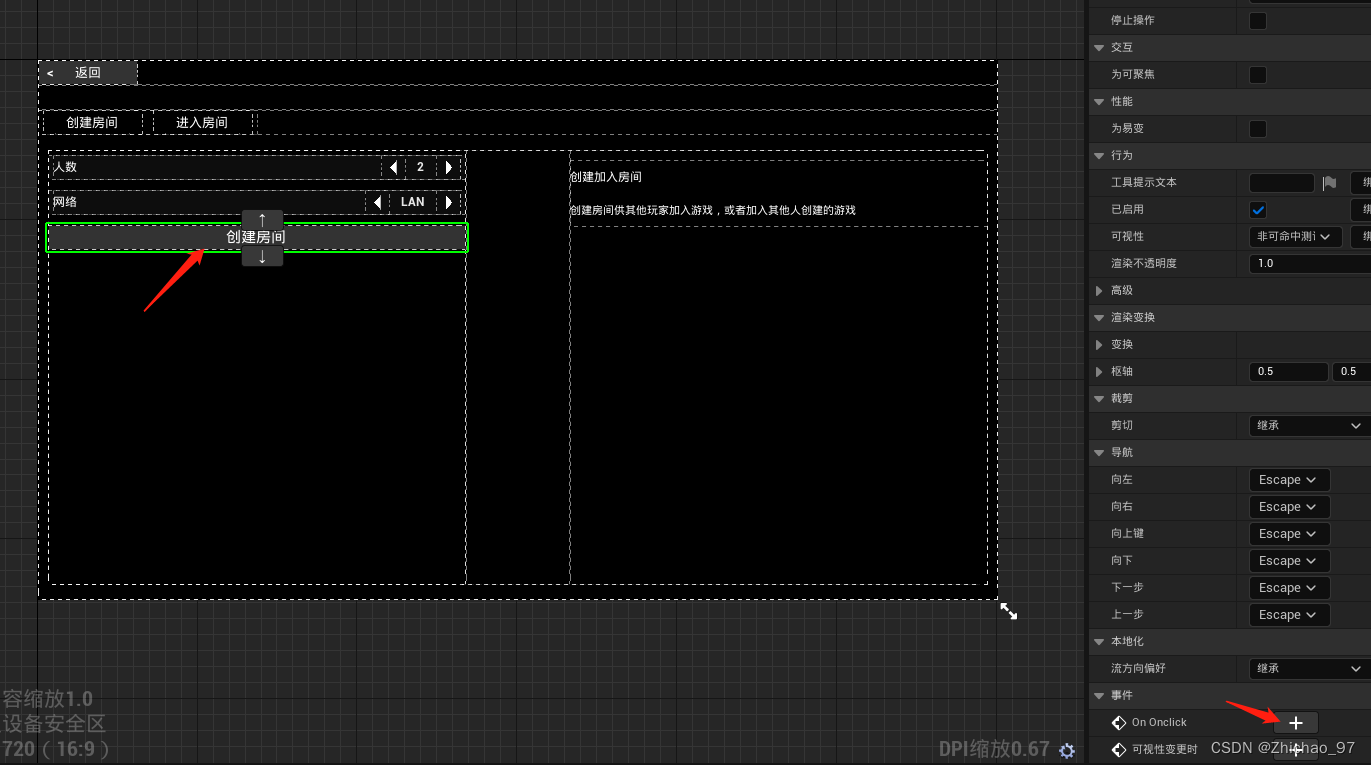
【UE5 多人联机教程】02-开始游戏菜单控件
目录 步骤 一、完善开始游戏菜单控件 二、控件功能实现 2.1 “开始游戏”按钮切换界面 2.2 “创建房间”、“加入房间”按钮切换界面 2.3 “创建房间”按钮 步骤 一、完善开始游戏菜单控件 打开“UMG_Main” 首先在控件切换器外层包裹一个画布面板 然后调整控件切换器全…...
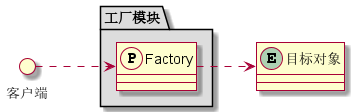
设计模式-工厂方法模式
基于面向对象语言开发中,免不得需要创建对象。前面讲解的"单例模式"也是如此,不过是要创建唯一的对象。本文要讲述“工厂方法模式”是要封装创建对象的过程。工厂,也称之为“制造厂”,用于创建具体的产品直接提供给外界…...
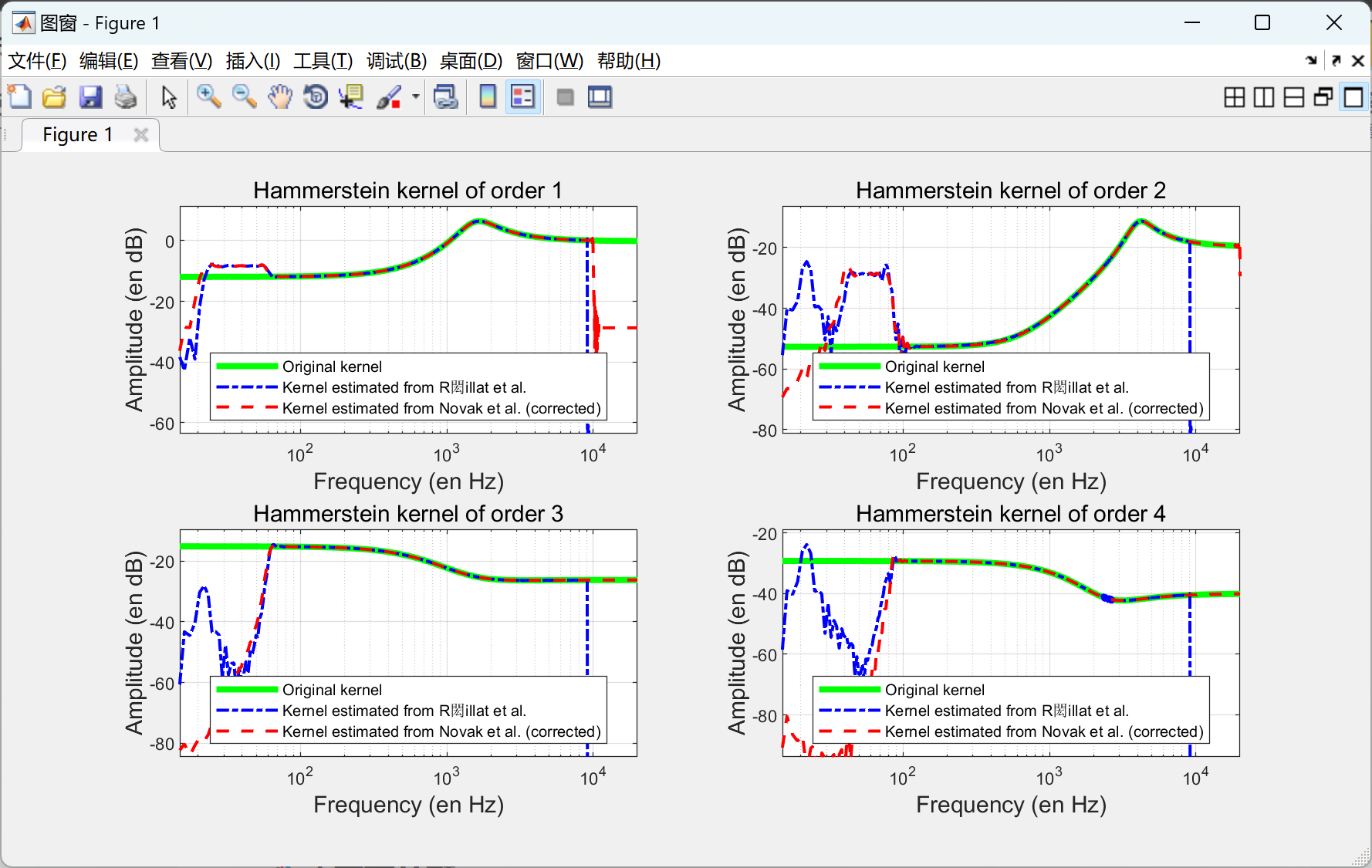
【Hammerstein模型的级联】快速估计构成一连串哈默斯坦模型的结构元素研究(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 🌈4 Matlab代码实现 💥1 概述 在许多振动应用中,所研究的系统略微非线性。Hammerstein模型的级联可以方便地描述这样的系统。Hammerstein提供了一种基于指数正弦…...

「C 语言」extern关键字
在 C 语言中,关键字 extern 是用来告诉编译器,这个变量 OR 函数在其他文件中已有定义,可在当前文件中使用 当我们定义了一个全局变量 OR 函数时,它就已经具有了外部链接的属性,我们只需要通过在引用该变量的文件中用 …...
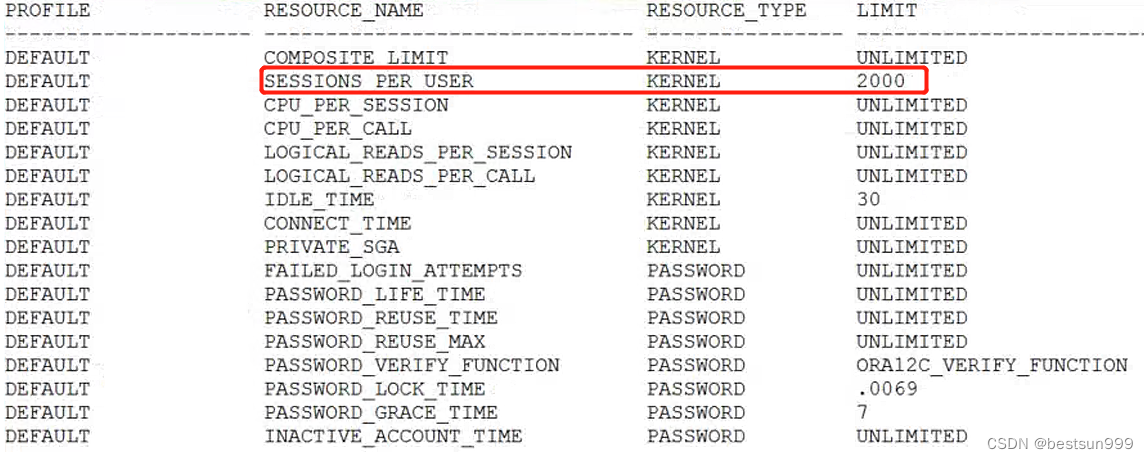
oracle单个用户最大连接数限制
项目经理反馈,现场已做了单个用户的最大连接数2000的限制,但数据库还是报无法连接,故障用户的连接数已3800多了。 查看日志报错如下 2023-07-20T13:07:57.79465308:00 Process m000 submission failed with error 20 Process m000 submiss…...

计算机网络最基础知识介绍
OSI和TCP/IP是很基础但又非常重要的知识,很多知识点都是以它们为基础去串联的,作为底层,掌握得越透彻,理解上层时会越顺畅。今天这篇网络基础科普,就是根据OSI层级去逐一展开的。 01 计算机网络基础 01 计算机网络的分类 按照网络的作用范围:广域网(WAN)、城域网(MA…...

接口测试进阶之数据模板
大家好久不见了。今天的文章将介绍jinja2模板在接口测试数据上的应用。 这几个月我在想,进阶系列要怎么写。 毕竟很多情况下,我觉得写技术文章和做培训一样,都会有两个结果: 1.是需要这些知识的人看不懂。 2.是看得懂的人不需要…...

Java中使用MySQL详解
1. 简介 在Java开发中,与数据库的交互是常见且重要的一部分。MySQL是一个广泛使用的关系型数据库管理系统,而Java作为一种强大的编程语言,提供了丰富的API和工具,使得与MySQL数据库的结合应用更加便捷和高效。 本篇博客将详细介…...

Docker安装Elasticsearch相关软件安装
Docker安装Elasticsearch相关软件安装 本文将介绍通过 Docker 的方式安装 Elasticsearch 相关的软件。 1、Docker安装Elasticsearch 1.1 搜索镜像 $ docker search elasticsearch $ docker search elasticsearch:7.12.11.2 拉取镜像 $ docker pull elasticsearch:7.12.11.…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...
