【Hammerstein模型的级联】快速估计构成一连串哈默斯坦模型的结构元素研究(Matlab代码实现)
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
在许多振动应用中,所研究的系统略微非线性。Hammerstein模型的级联可以方便地描述这样的系统。Hammerstein提供了一种基于指数正弦扫描相位属性的简单方法。
构成一连串Hammerstein模型的结构元素可以在快速估计中起到关键的作用。Hammerstein模型由级联的非线性静态函数和线性动态函数组成。以下是研究Hammerstein模型结构元素的步骤:
1. 数据收集:首先,收集用于建立Hammerstein模型的数据。这些数据应包括系统的输入和输出信号,以便进行模型参数估计和验证。
2. 静态非线性函数选择:选择适当的静态非线性函数作为Hammerstein模型的非线性部分。常见的选择包括多项式函数、幂函数、指数函数、Sigmoid函数等。根据系统的特性和预期的非线性行为,选择最能表示系统的非线性特点的函数。
3. 参数估计:对选择的静态非线性函数进行参数估计。参数估计的方法可以根据函数的性质灵活选择,例如最小二乘法、最大似然估计法等。根据所选方法,使用数据集中的输入和输出信号优化非线性函数的参数。
4. 线性动态函数选择:选择适当的线性动态函数作为Hammerstein模型的动态部分。常见的选择包括传递函数、状态空间模型等。根据系统的动态特性,选择最适合描述系统响应的线性动态函数。
5. 参数估计:对选择的线性动态函数进行参数估计。使用数据集中的输入和输出信号,在模型的非线性部分和线性动态部分之间优化参数。
6. 模型验证:使用建立的Hammerstein模型对独立数据集进行验证。计算预测输出与真实输出之间的误差,评估模型的准确性和可靠性。如果有必要,可以对模型进行进一步调整和改进。
7. 性能分析:对Hammerstein模型的性能进行分析。例如,可以通过计算模型的拟合优度(如均方根误差)来评估模型的准确性。此外,还可以进行稳定性分析、系统辨识度评估等进一步分析。
需要注意的是,构建Hammerstein模型需要对非线性和线性组成部分的选择和参数估计进行适当的判断和调整。根据具体问题的复杂性和数据的可用性,可以采用各种方法和技术来加快估计和验证过程。
📚2 运行结果
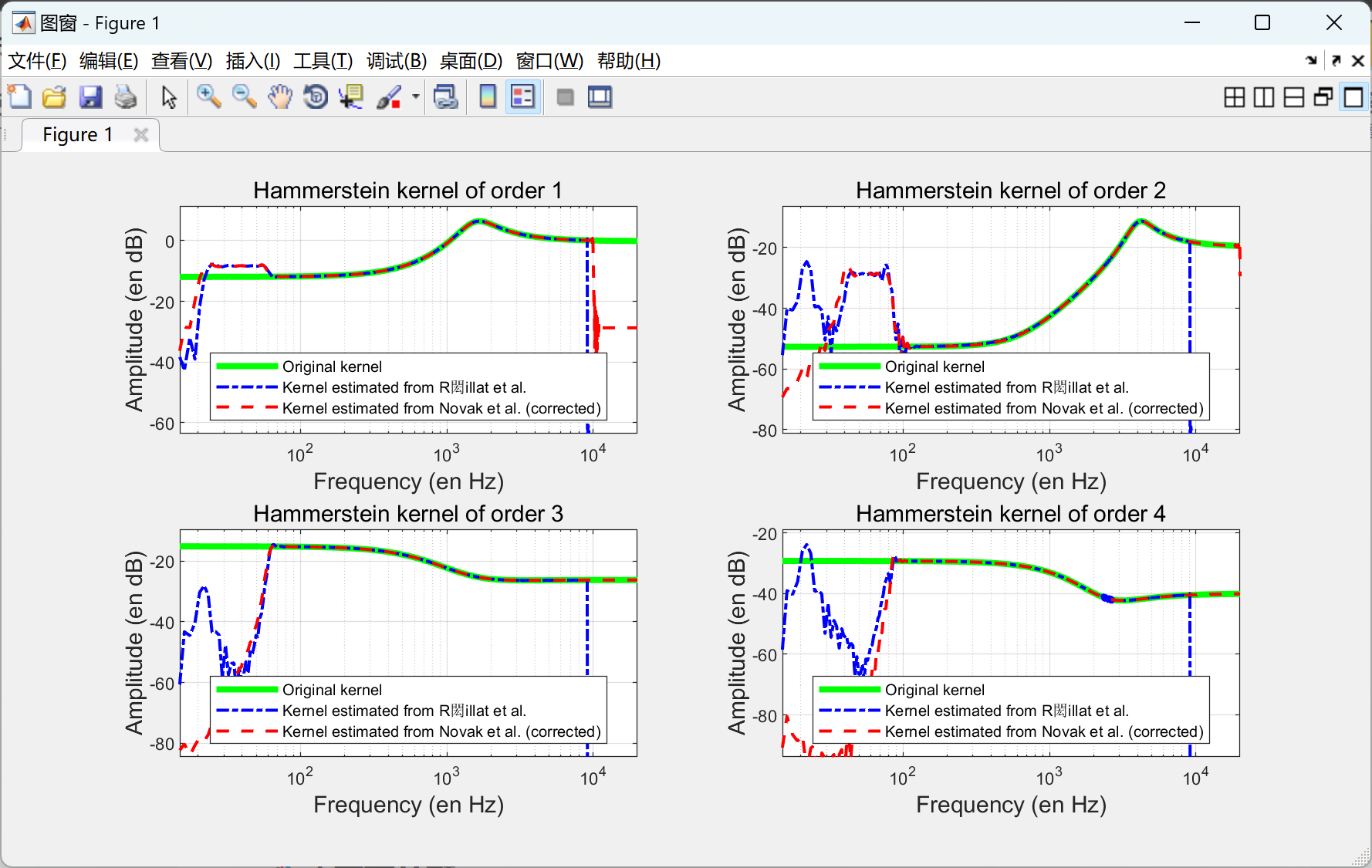
部分代码:
function hhat = Hammerstein_ID(input_sig,output,duration,f1,f2,fs,N,opt_meth,opt_filt)
%---------------------------------------------------------
%
% hhat = Hammerstein_ID(input_sig,output,f1,f2,fs,N,opt_meth,opt_filt)
%
% Estimates the Kernels "h" of the cascade of Hammerstein model of order N fed with
% the input signal "input" and where the corresponding output signal "output"
% has been recorded. "input" has to be an exponential sine sweep going from
% f1 to f2.
%
% Input parameters:
% input_sig : input exponential sine sweep
% output : output of the system fed with the input signal
% f1 : starting frequency of the sweep
% f2 : end frequency of the sweep
% fs : sampling frequency
% N : Order of the model to be identified
% opt_meth : Method to use for the estimation (string expected)
% - 'Reb': Method proposed by R閎illat et al. in [1]
% - 'Nov': Method proposed by Novak et al in [2]
% opt_filt : Specifies the method to use to compute the inverse filter
% (string expected). By default 'TFB_linear' is chosen.
% - 'TFB_square': FTT based filter with a square window and
% regularization (see [1])
% - 'TFB_linear': FTT based filter with a square window with continuous
% linear borders and regularization (see [1])
% - 'TFB_gevrey': FTT based filter with a square window with infinitely
% continuous gevrey borders and regularization (see [1])
% - 'Nov' : Filter based on the analytical formulation using aymptotic
% signals (see [2]).
%
% Output:
% h : 2D matrix containing the pseudo impulse responses (temporal domain)
% of the estimated kernels.
display('--> Hammerstein Identification in progress ...')
% Check arguments
if nargin<6
display(' => ERROR : Incorrect number of arguments')
return
elseif nargin<7
display(' => No method option and filtering option specified. ')
display(' => Method option = ''Reb'' chosen by default.')
display(' => Filtering option = ''TFB_linear'' chosen by default.')
opt_meth = 'Reb' ;
opt_filt = 'TFB_linear';
elseif nargin<8
display([' => Method ' opt_meth ' chosen'])
display(' => No filtering option specified. ')
if strcmp(opt_meth,'Reb')
opt_filt = 'TFB_linear';
display(' => Filtering option = ''TFB_linear'' chosen by default.')
elseif strcmp(opt_meth,'Nov')
opt_filt = 'Nov';
display(' => Filtering option = ''Nov'' chosen by default.')
else
display(' => ERROR : Unknown method option')
display(' => Select ''Reb'' or ''Nov''')
return
end
else
if ( strcmp(opt_meth,'Nov') || strcmp(opt_meth,'Reb'))
display([' => Method ' opt_meth ' chosen'])
else
display(' => ERROR : Unknown method option')
display(' => Select ''Reb'' or ''Nov''')
return
end
if ( strcmp(opt_filt,'TFB_square') || strcmp(opt_filt,'TFB_linear') || strcmp(opt_filt,'TFB_gevrey') || strcmp(opt_filt,'Nov'))
display([' => Filtering ' opt_filt ' chosen'])
else
display(' => ERROR : Unknown filtering option')
display(' => Select ''TFB_square'', ''TFB_linear'', ''TFB_gevrey'' or ''Nov''')
return
end
end
% Equivalent pulsations
w1 = f1/fs*2*pi;
w2 = f2/fs*2*pi;
% Convolution of the response with the inverse of the sweep
if strcmp(opt_meth,'Reb')
inverse_input_sig = compute_inverse_filter(input_sig,f1,f2,fs,opt_filt) ;
gToCut = convq(output,inverse_input_sig);
elseif strcmp(opt_meth,'Nov')
% Nonlinear convolution in the spectral domain
gToCut = nonlinear_convolution(output,duration,f1,f2,fs);
gToCut = [gToCut; gToCut];
end
% Computation of the delay of the pseudo RI
if strcmp(opt_meth,'Reb')
T = length(input_sig); % Actual length of the sweep (in samples)
deltaT = T*log(1:N)/log(w2/w1);
elseif strcmp(opt_meth,'Nov')
T = length(output); % Actual length of the output (in samples)
L = 1/f1*round( (duration*f1)/(log(f2/f1)) );
deltaT = L*log(1:N)*fs;
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1] M. Rébillat, R. Hennequin, E. Corteel, B.F.G. Katz, "Identification of cascade of Hammerstein models for the description of non-linearities in vibrating devices", Journal of Sound and Vibration, Volume 330, Issue
5, Pages 1018-1038, February 2011.
[2] A. Novak, L. Simon, F. Kadlec, P. Lotton, "Nonlinear system identification using exponential swept-sine signal", IEEE Transactions on Instrumentation and Measurement, Volume 59, Issue 8, Pages 2220-2229, August 2010.
🌈4 Matlab代码实现
相关文章:

【Hammerstein模型的级联】快速估计构成一连串哈默斯坦模型的结构元素研究(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 🌈4 Matlab代码实现 💥1 概述 在许多振动应用中,所研究的系统略微非线性。Hammerstein模型的级联可以方便地描述这样的系统。Hammerstein提供了一种基于指数正弦…...

「C 语言」extern关键字
在 C 语言中,关键字 extern 是用来告诉编译器,这个变量 OR 函数在其他文件中已有定义,可在当前文件中使用 当我们定义了一个全局变量 OR 函数时,它就已经具有了外部链接的属性,我们只需要通过在引用该变量的文件中用 …...
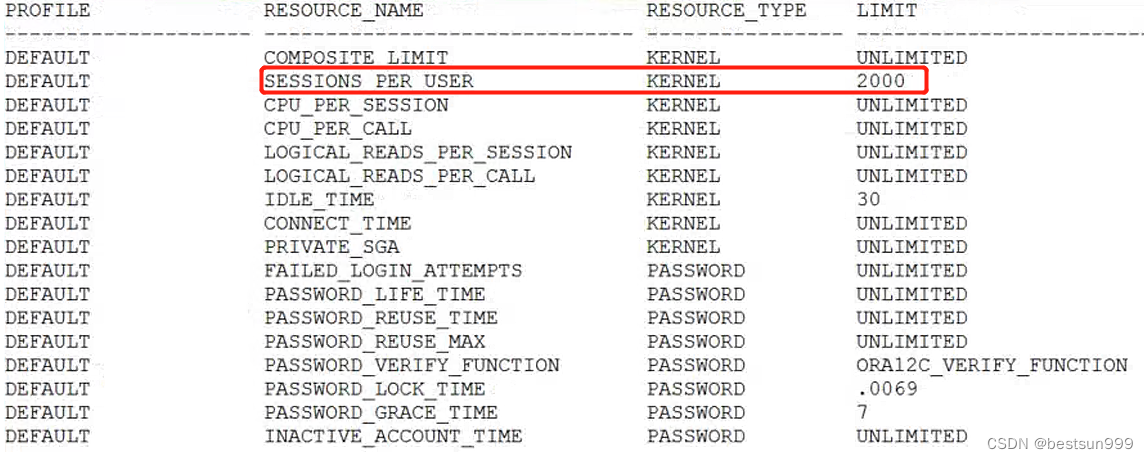
oracle单个用户最大连接数限制
项目经理反馈,现场已做了单个用户的最大连接数2000的限制,但数据库还是报无法连接,故障用户的连接数已3800多了。 查看日志报错如下 2023-07-20T13:07:57.79465308:00 Process m000 submission failed with error 20 Process m000 submiss…...

计算机网络最基础知识介绍
OSI和TCP/IP是很基础但又非常重要的知识,很多知识点都是以它们为基础去串联的,作为底层,掌握得越透彻,理解上层时会越顺畅。今天这篇网络基础科普,就是根据OSI层级去逐一展开的。 01 计算机网络基础 01 计算机网络的分类 按照网络的作用范围:广域网(WAN)、城域网(MA…...

接口测试进阶之数据模板
大家好久不见了。今天的文章将介绍jinja2模板在接口测试数据上的应用。 这几个月我在想,进阶系列要怎么写。 毕竟很多情况下,我觉得写技术文章和做培训一样,都会有两个结果: 1.是需要这些知识的人看不懂。 2.是看得懂的人不需要…...

Java中使用MySQL详解
1. 简介 在Java开发中,与数据库的交互是常见且重要的一部分。MySQL是一个广泛使用的关系型数据库管理系统,而Java作为一种强大的编程语言,提供了丰富的API和工具,使得与MySQL数据库的结合应用更加便捷和高效。 本篇博客将详细介…...

Docker安装Elasticsearch相关软件安装
Docker安装Elasticsearch相关软件安装 本文将介绍通过 Docker 的方式安装 Elasticsearch 相关的软件。 1、Docker安装Elasticsearch 1.1 搜索镜像 $ docker search elasticsearch $ docker search elasticsearch:7.12.11.2 拉取镜像 $ docker pull elasticsearch:7.12.11.…...
Ubuntu的安装与部分配置
该教程使用的虚拟机是virtuabox,镜像源的版本是ubuntu20.04.5桌面版 可通过下面的链接在Ubuntu官网下载:Alternative downloads | Ubuntu 也可直接通过下面的链接进入百度网盘下载【有Ubuntu20.04.5与hadoop3.3.2以及jdk1.8.0_162,该篇需要使…...

为什么 Splashtop 是更好用的 iOS 远程桌面应用
全球远程桌面软件市场最近达到19.2亿美元,表明使用任意设备实现随处远程控制越来越受欢迎。 近年来,企业的运营方式发生了重大改变,远程桌面软件已成为广泛使用的解决方案。Splashtop 是目前最好用的远程桌面工具之一,安全可靠且…...

[SQL挖掘机] - 字符串函数 - lower
介绍: lower函数是mysql中的一个字符串函数,其作用是将给定的字符串转换为小写形式。它接受一个字符串作为参数,并返回一个新的字符串,其中所有的字母字符均被转换为小写形式。 使用lower函数可以帮助我们在字符串处理中实现标准化和规范化…...
什么是Koala?
Koala 介绍 koala 是一个前端预处理器语言图形编译工具,支持 Less、Sass、Compass、CoffeeScript,帮助 web 开发者更高效地使用它们进行开发。跨平台运行,完美兼容 windows、linux、mac。 关键特性 多语言支持 支持 Less、Sass、CoffeeSc…...

阿里巴巴前端开发规范
前言 规范的目的是为了编写高质量的代码,让你的团队成员每天的心情都是愉悦的,大家在一起是快乐的。 现在软件架构的复杂性需要协同开发完成,如何高效地协同呢?无规矩不成方圆,无规范难以协同,比如…...
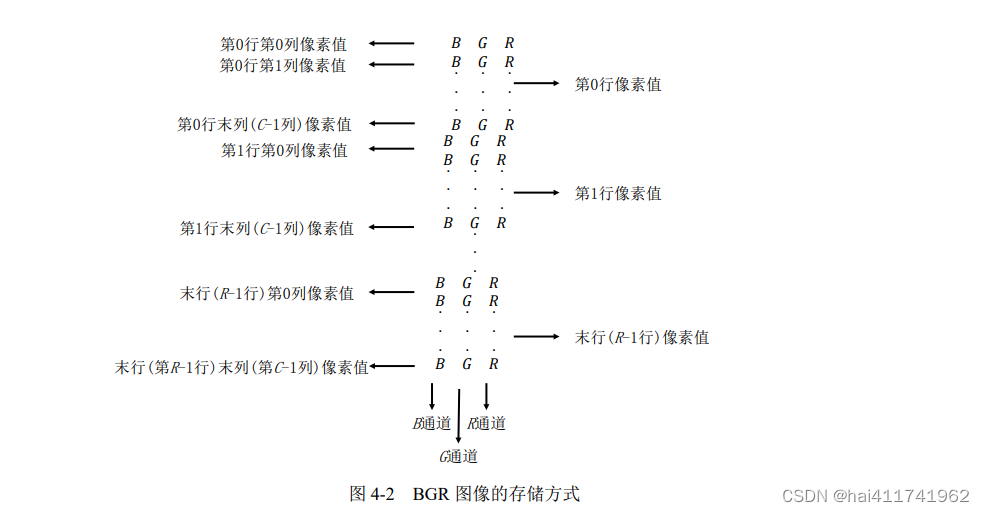
opencv-19 图像色彩空间转换函数cv2.cvtColor()
cv2.cvtColor() 函数是 OpenCV 中用于图像颜色空间转换的函数。它允许你将图像从一个色彩空间转换为另一个色彩空间。在 Python 中,你可以使用这个函数来实现不同色彩空间之间的转换。 函数的基本语法为: cv2.cvtColor(src, code[, dst[, dstCn]])参数…...
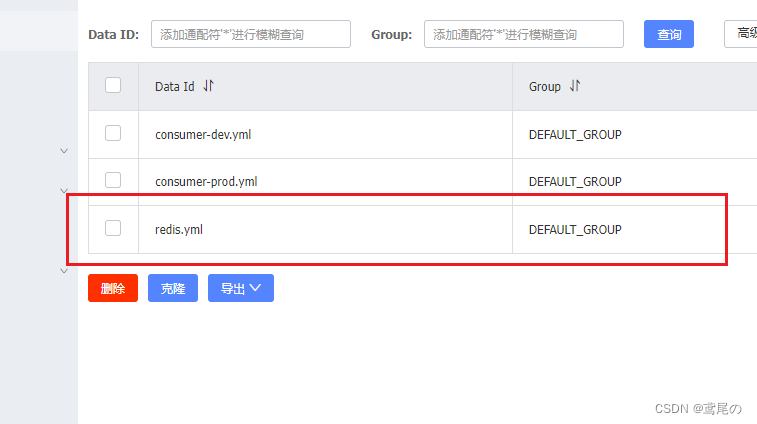
SpringCloudAlibaba微服务实战系列(二)Nacos配置中心
SpringCloudAlibaba Nacos配置中心 在java代码中或者在配置文件中写配置,是最不雅的,意味着每次修改配置都需要重新打包或者替换class文件。若放在远程的配置文件中,每次修改了配置后只需要重启一次服务即可。话不多说,直接干货拉…...

【Kafka源码走读】Admin接口的客户端与服务端的连接流程
注:本文对应的kafka的源码的版本是trunk分支。写这篇文章的主要目的是当作自己阅读源码之后的笔记,写的有点凌乱,还望大佬们海涵,多谢! 最近在写一个Web版的kafka客户端工具,然后查看Kafka官网,…...

Windows API遍历桌面上所有文件
要获取桌面上的图标,可以使用Windows API中的Shell API。以下是遍历桌面上所有文件的示例代码: #include <Windows.h> #include <ShlObj.h> #include <iostream> #include <vector> using namespace std;int main() {// 获取桌…...
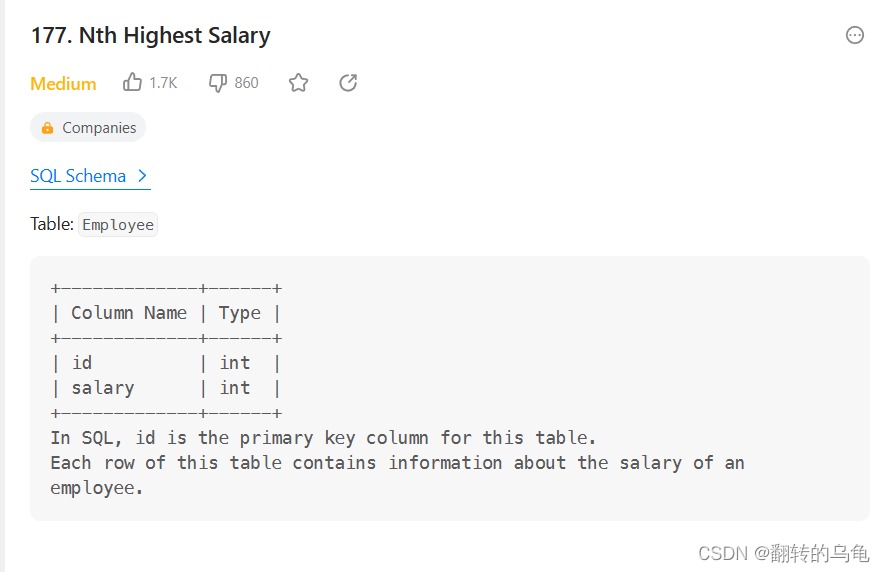
【MySQL】基本查询(插入查询结果、聚合函数、分组查询)
目录 一、插入查询结果二、聚合函数三、分组查询(group by & having)四、SQL查询的执行顺序五、OJ练习 一、插入查询结果 语法: INSERT INTO table_name [(column [, column ...])] SELECT ...案例:删除表中重复数据 --创建…...
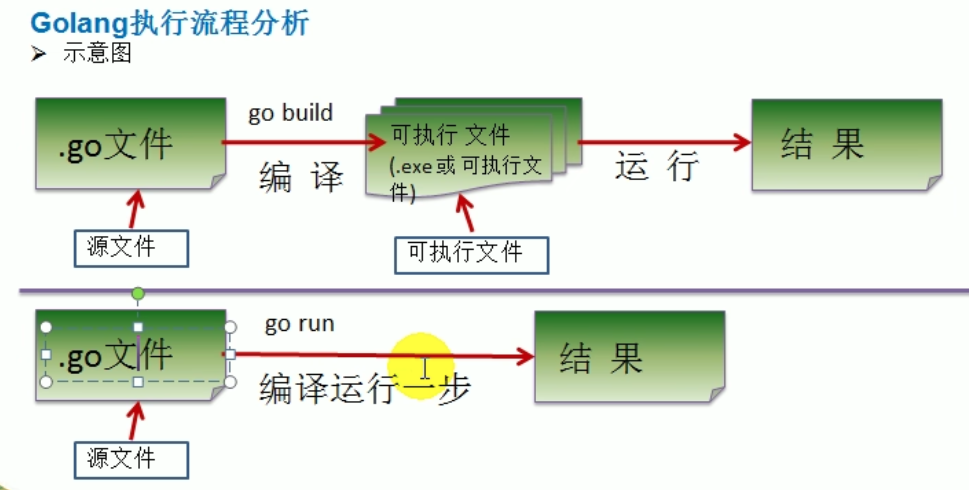
【Go语言】Golang保姆级入门教程 Go初学者介绍chapter1
Golang 开山篇 Golang的学习方向 区块链研发工程师: 去中心化 虚拟货币 金融 Go服务器端、游戏软件工程师 : C C 处理日志 数据打包 文件系统 数据处理 很厉害 处理大并发 Golang分布式、云计算软件工程师:盛大云 cdn 京东 消息推送 分布式文…...

mysql 自增长键值增量设置
参考文章 MySQL中auto_increment的初值和增量值设置_auto_increment怎么设置_linda公馆的博客-CSDN博客 其中关键语句 show VARIABLES like %auto_increment% set auto_increment_increment4; set auto_increment_offset2;...
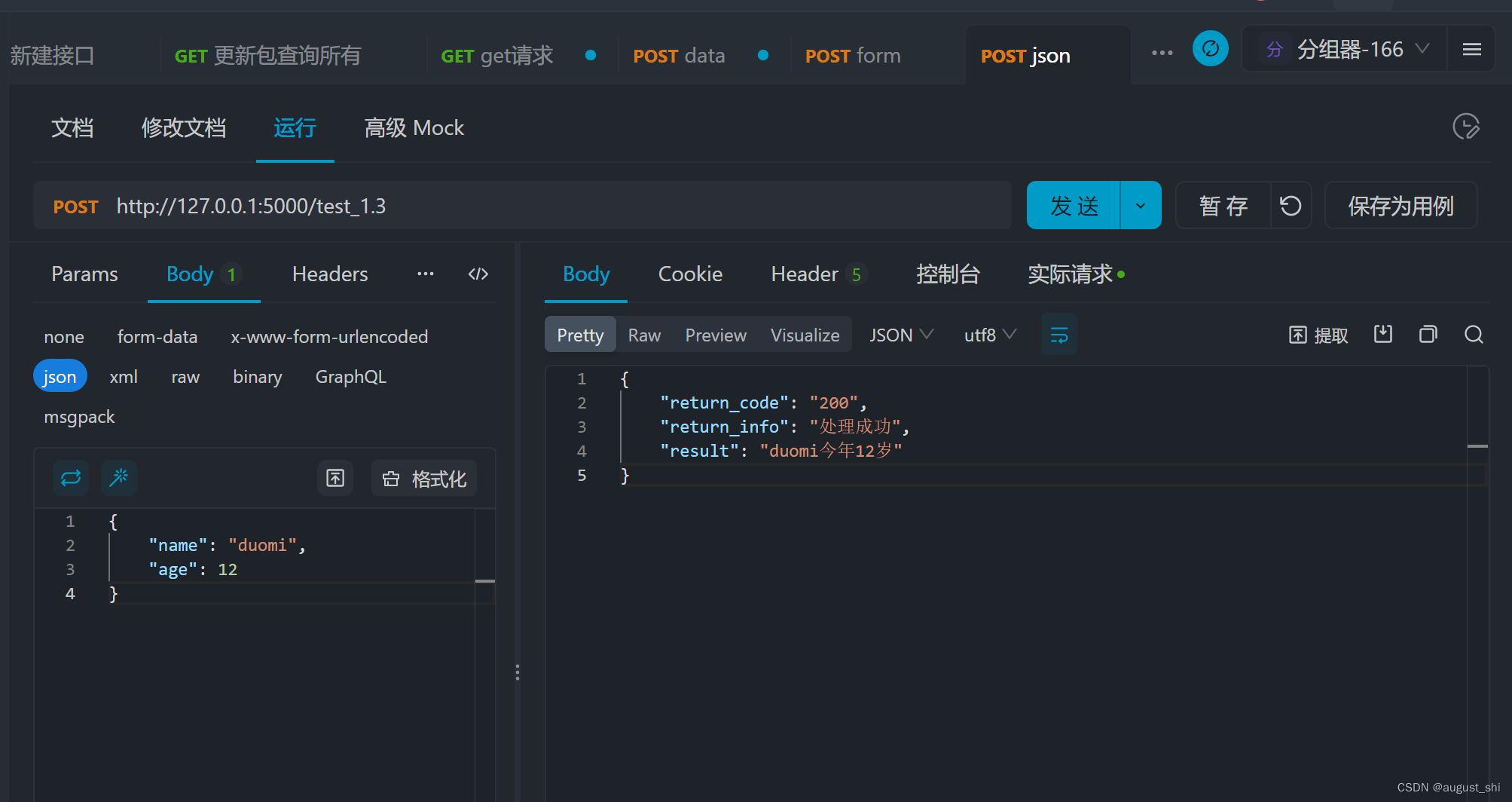
【pytho】request五种种请求处理为空和非空处理以及上传excel,上传图片处理
一、python中请求处理 request.args获取的是个字典,所以可以通过get方式获取请求参数和值 request.form获取的也是个字典,所以也可以通过get方式获取请求的form参数和值 request.data,使用过JavaScript,api调用方式进行掺入jso…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

