2023杭电多校第三场 1012.Noblesse Code
传送门:Vjudge
前题提要:一道挺有意思的数论题.赛时对于这道题没什么想法,但是赛后细品之后其实感觉也就那么一回事.但是这种 更相损减术与辗转相除法 相转化的题目还是有点典的,需要好好消化一下.
首先看完题目.我们需要考虑的是 ( A , B ) (A,B) (A,B)与 ( a , b ) (a,b) (a,b)的相互转化关系.其中转化方法是使用类似于更相损减术的方法.显然.我们是不能直接转化的,因为对于更相损减术来说,如果 ( A , B ) (A,B) (A,B)两个数相差太大,那么需要的复杂度就会爆炸.所以我们得考虑一种更有效率的方法.
因为是更相损减术,所以我们联想到它的好兄弟,辗转相除法.辗转相除法可以很好的解决更相损减术过程中不断的单向减少的过程(也就是不断的变为 ( a , b − a ) (a,b-a) (a,b−a)).但是使用辗转相除法处理我们的 ( A , B ) (A,B) (A,B)的话,显然会丢失中间的一些数对.就比如 ( 9 , 3 ) (9,3) (9,3),我们使用辗转相除法,进行一次就会得到 ( 0 , 3 ) (0,3) (0,3),此时我们会丢失中途本来可以得到的 ( 6 , 3 ) , ( 3 , 3 ) (6,3),(3,3) (6,3),(3,3)等数对,并且这些数对都是符合题意的,那么我们该怎么解决这种问题呢.
考虑我们的辗转相除法是解决更相损减术固定一个值,另一个值不断减少的过程,所以在这过程中我们舍掉的这些数对必然是一个端点和我们的初始端点相同,另一个端点成等差数列分布.也就是上述中的 9 , 6 , 3 , 0 9,6,3,0 9,6,3,0.并且我们需要知道的是,假设我们对初始的 ( A , B ) (A,B) (A,B)进行更相损减术操作,我们后面得到的数对都是一一对应的,也就是 ( A , B ) (A,B) (A,B)得到 ( a , b ) (a,b) (a,b)我们的 ( a , b ) (a,b) (a,b)就能通过题面中的操作重新变成 ( A , B ) (A,B) (A,B).所以此时考虑我们需要解决的问题,假设我们的 ( a i , b i ) (ai,bi) (ai,bi)能通过题面中的操作变成(A,B),我们的 ( a i , b i ) (ai,bi) (ai,bi)必然处于我们的 ( A , B ) (A,B) (A,B)的变化链中.
那么我们可以考虑记录对 ( A , B ) (A,B) (A,B)的辗转相除法的过程,也就是记录每一次辗转相除法之后的数.如果我们将数看做节点,那么我们相对于更相损减术省略掉的那些点就在我们的两两节点相连的链上.更一般的,我们可以将整个过程看成一棵树.那么对于所有的(A,B)树来说,就是一颗森林.那么对于我们的 ( a i , b i ) (ai,bi) (ai,bi)来说,假设这个数对刚好是(A,B)树中的一个节点.那么显然的我们的 ( a i , b i ) (ai,bi) (ai,bi)可以变为 ( A , B ) (A,B) (A,B).如果不是节点的话,那么我们需要将 ( a i , b i ) (ai,bi) (ai,bi)进行一次辗转相除法操作,因为这样我们就可以将(ai,bi)转化成一个森林上的一个节点(原因是显然的,因为我们森林中的一个节点必然是一次辗转相除法之后的结果),那么对于此时新的 ( a , b ) (a,b) (a,b),我们就知道假设我们的 旧 ( a , b ) 旧(a,b) 旧(a,b)能转化成 ( A , B ) (A,B) (A,B),意味着我们的 ( A , B ) (A,B) (A,B)在我们的 ( a , b ) (a,b) (a,b)这个节点的上面(此处的上面是指(A,B)能转化成新(a,b),并且(A,B)能转化成旧(a,b)).又因为对于在同一条链上的点来说,我们是很容易知道哪一个数固定,哪一个数成等差的(比一下大小即可).所以对于我们的合法的 ( A , B ) (A,B) (A,B)与 ( a , b ) (a,b) (a,b)来说,(A,B)中成等差的那一个数必然比 ( a , b ) (a,b) (a,b)中要大.(此处我们可以使用二分).
其实到这里我们的 t r i c k trick trick基本上就详细的讲完了.接下来讲讲具体做法(仅供参考)
乍一看对于每一节点似乎都是一个二叉树,但是仔细看发现一个简单的性质.假设我们的节点为 ( a , b ) (a,b) (a,b),我们此时 a < b a<b a<b的话,那么对于某个在它上面的 ( A , B ) (A,B) (A,B)来说,我们此时必然是有 A > B A>B A>B的,反之则( B > A B>A B>A).原因考虑辗转相除法的性质,此处不在赘述.同样的,我们发现不可能存在一个节点 ( a = b ) (a=b) (a=b).(这里的点是指辗转相除法过程中的节点,而不是之前所说的 ( a i , b i ) (ai,bi) (ai,bi))
考虑使用 v e c t o r vector vector来记录每一个节点的点对以及它的成等差的数的端点.就比如 ( 9 , 6 ) (9,6) (9,6),我们进行一次操作得到 ( 3 , 6 ) (3,6) (3,6),我们记录点对 ( 3 , 6 ) (3,6) (3,6),并且将 9 9 9存到 v e c t o r vector vector中,这意味着假设我们之后的 ( a i . b i ) (ai.bi) (ai.bi)是 ( 3 , 6 ) (3,6) (3,6)的话,我们的 9 9 9比 6 6 6大,所以可以转化.那么对于一个点对来说,我们可能有很多个 ( A , B ) (A,B) (A,B)可以到达它,此时,我们需要存下每一个端点,然后在 ( a i , b i ) (ai,bi) (ai,bi)的时候直接用二分来查找有一个满足端点大于即可.
这里还有一个小细节需要注意,那就是当我们的 ( a i , b i ) (ai,bi) (ai,bi)中 a i = b i ai=bi ai=bi时,我们此时转化方法并不是单向的,而是双向的.也就是一个点处于两条链中.所以此时我们需要同时加上 ( a i , 0 ) , ( 0 , b i ) (ai,0),(0,bi) (ai,0),(0,bi)的结果.除此之外,根据辗转相除法的性质,其他点必不能同时处于两条链上.(因为既要 a > = b , b > = a a>=b,b>=a a>=b,b>=a那么只能相等)
下面是具体的代码部分(前文已足够详尽,代码不再补充注释):
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
inline void print(__int128 x){if(x<0) {putchar('-');x=-x;}if(x>9) print(x/10);putchar(x%10+'0');
}
#define maxn 1000000
#define int long long
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
map<pair<int,int>,vector<int>>tree;
void build(int a,int b) {if(a==0||b==0) return ;if(a<=b) {tree[make_pair(a,b%a)].push_back(b);build(a,b%a);}else {tree[make_pair(a%b,b)].push_back(a);build(a%b,b);}
}
signed main() {int T=read();while(T--) {tree.clear();int n=read();int q=read();for(int i=1;i<=n;i++) {int A=read();int B=read();build(A,B);}for(auto &it:tree) {sort(it.second.begin(),it.second.end());}for(int i=1;i<=q;i++) {int a=read();int b=read();if(a==b) {cout<<tree[make_pair(a,0)].size()+tree[make_pair(0,b)].size()<<endl;}else if(a<b) {pair<int,int>last_node=make_pair(a,b%a);auto pos=lower_bound(tree[last_node].begin(),tree[last_node].end(),b);cout<<tree[last_node].end()-pos<<endl;}else {pair<int,int>last_node=make_pair(a%b,b);auto pos=lower_bound(tree[last_node].begin(),tree[last_node].end(),a);cout<<tree[last_node].end()-pos<<endl;}}}return 0;
}
相关文章:

2023杭电多校第三场 1012.Noblesse Code
传送门:Vjudge 前题提要:一道挺有意思的数论题.赛时对于这道题没什么想法,但是赛后细品之后其实感觉也就那么一回事.但是这种 更相损减术与辗转相除法 相转化的题目还是有点典的,需要好好消化一下. 首先看完题目.我们需要考虑的是 ( A , B ) (A,B) (A,B)与 ( a , b ) (a,b) (…...

ubuntu qt 环境变量配置
ubuntu设置qt环境变量 qt 安装路径为:/home/ljn/Qt5.12 包含bin等目录的路经:/home/ljn/Qt5.14.2/5.14.2/gcc_64 环境变量配置 打开配置文件: sudo gedit /etc/profile在底部添加: export PATH"/home/ljn/Qt5.14.2/Tool…...
:功能实现)
按照Vue写WPF(0):功能实现
文章目录 前言VUE具有的功能如何专业到WPF上面 前言 我最近学了WPF之后我终于知道为什么WPF学习曲线那么陡峭了。因为WPF没有组件化的思想,或者说没有按照Vue一样去模板化开发。 为什么我推荐Vue的想法呢。因为Vue最大的特点就是模板化,让Vue工程师去写…...

vb+ACCESS教师管理系统设计设计与实现
--------------前言-------------- 教师管理系统是一个企事业单位不可缺少的部分,它的内容对于企事业单位的决策者和管理者来说都至关重要,所以教师管理系统应该能够为用户提供充足的信息和快捷的查询手段。但一直以来人们使用传统人工的方式管理文件信息,这种管理方式存在…...

C++笔记之对指针类型的变量进行+1操作
C笔记之对指针类型的变量进行1操作 在C中,对指针类型的变量进行"1"操作会根据指针的数据类型而有所不同。这涉及到指针的算术运算,C中的指针算术运算是根据指针所指向的数据类型的大小来进行的。 code review! 文章目录 C笔记之对指针类型的…...

第六章 游标
游标 本文内容较短,我们只是为了更容易的实现b树,简单地重构一下。 我们将添加一个Cursor 表示表中对象的位置。Cursor应提供如下几个方面的能力: 在表的开头创建游标在表的末尾创建游标访问游标指向的行将游标前进到下一行 这是本文我们…...
Github上方导航栏介绍
Code Watch:相当于关注,到时候这个项目又有什么操作,就会以通知的形式提醒你。 Fork:也就是把这个项目拉到你的仓库里,之后你可以对该代码进行修改,之后你可以发起Pull Request,简称PR…...
)
【vue3+ts】TypeError: Cannot read properties of undefined (reading ‘commit‘)
项目场景: <script lang"ts"> import { defineComponent, reactive, ref } from vue import { useStore } from vuex export default defineComponent({name: Login.vue,components: {},setup () {const onFormSubmit (result: boolean) > {if…...

seq2seq、attention、self-attention、transformer、bert
seq2seq seq2seq:输入序列,输出序列,将输入的语言转为一个向量,最后输出再将向量转为语言shortcoming:The final state is incapable of remembering a long sequence.即太长了记不住 attention 用attention可以改进seq2seq中的…...

07.计算机网络——数据链路层
文章目录 数据链路层以太网帧格式MAC地址理解MAC地址和IP地址认识MTUMTU对IP协议的影响MTU对UDP协议的影响MTU对于TCP协议的影响 ARP协议**ARP**协议的作用ARP协议的工作流程ARP数据报的格式 数据链路层 数据链路层在物理层提供的服务的基础上向网络层提供服务,…...

海外服务器推荐:国外高性能服务器免费
对于寻找高性能的海外服务器,海外服务器推荐指导,我建议您考虑以下因素: 1. 可靠性和性能:选择信誉良好、可靠性好的服务器提供商。它们应该有稳定的网络基础设施和高性能的服务器硬件来满足您的需求。 2. 位置选择:…...
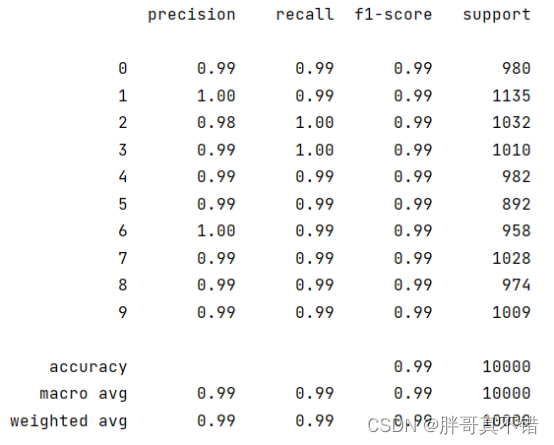
Python基于PyTorch实现卷积神经网络分类模型(CNN分类算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 卷积神经网络,简称为卷积网络,与普通神经网络的区别是它的卷积层内的神经元只覆…...
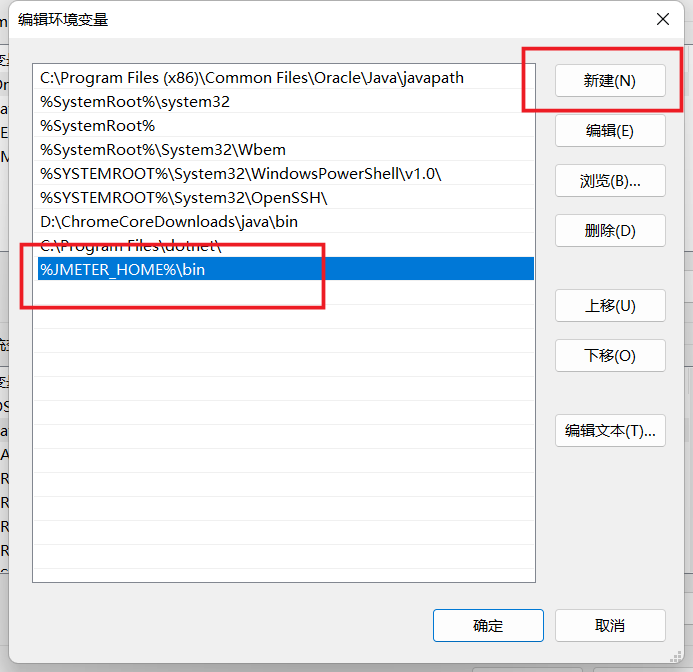
JMeter 配置环境变量步骤
通过给 JMeter 配置环境变量,可以快捷的打开 JMeter: 打开终端。执行 jmeter。 配置环境变量的方法如下。 Mac 和 Linux 系统 1、在 ~/.bashrc 中加如下内容: export JMETER_HOMEJMeter所在目录 export PATH$JAVA_HOME/bin:$PATH:.:$JME…...
Rust vs Go:常用语法对比(六)
题图来自[1] 101. Load from HTTP GET request into a string Make an HTTP request with method GET to URL u, then store the body of the response in string s. 发起http请求 package mainimport ( "fmt" "io/ioutil" "net" "net/http…...
css元素定位:通过元素的标签或者元素的id、class属性定位
前言 大部分人在使用selenium定位元素时,用的是xpath元素定位方式,因为xpath元素定位方式基本能解决定位的需求。xpath元素定位方式更直观,更好理解一些。 css元素定位方式往往被忽略掉了,其实css元素定位方式也有它的价值&…...

java享元模式
在Java中实现享元模式,可以通过创建一个享元工厂(FlyweightFactory)和享元对象(Flyweight)来完成。享元模式用于共享可复用对象,以节省内存和提高性能。 下面是一个简单的示例: 首先ÿ…...

ESP32(MicroPython) 两轮差速五自由度机械臂小车
这次的项目在软件上没多少调整,但本人希望分享一下硬件上的经验。 小车使用两轮差速底盘,驱动轮在小车中间,前后都要万向轮。这种形式可以实现0转弯半径,但受万向轮及用于加高的铜柱的规格限制,两个万向轮难以调到相同…...
)
mysql基本函数(五)
目录 一、数字函数二、字符函数三、日期时间函数3.1 获取系统日期时间的函数3.2 日期格式化函数3.3 日期偏移计算3.4 日期之间相隔的天数 四、条件函数4.1 IF语句4.2 条件语句 一、数字函数 函数功能用例ABS绝对值ABS(-100)ROUND四舍五入ROUND(4.62)FLOOR向下取值FLOOR(9.9)CE…...

liteflow 2.10 配置中心简单记录
除nacos是一个key 同时管理chain和script node外,可以理解为配置文件整体放到一个key下nacos下的文件必须是xml格式,系统只实现了xml parser其它etcd,zk,Apollo 是两个namespace/path(chain及script node各一)下多个key,每个key对应一个chain/node所有配置中心的核心代码…...

【C++】引用、内联函数等
文章目录 一、引用1.引用概念2.引用特性3.引用时的权限问题4 .使用场景5 .引用和指针的联系与区别 二、内联函数1.概念2.注意点 三、auto关键字1.概念2.auto的使用细则 四、 基于范围的for循环1.概念2.范围for的使用条件 五、 指针空值nullptr1.概念2.使用注意 一、引用 1.引用…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
