【leetcode】leetcode69 x的平方根
文章目录
- 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
- 原理
- 牛顿法(数值分析中使用到的):
- 二分法
- 解决方案
- java 实现
- 实例
- 执行结果
- python 实现
- 实例
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。
提示:
0 <= x <= 231 - 1
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/sqrtx
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
原理
牛顿法(数值分析中使用到的):
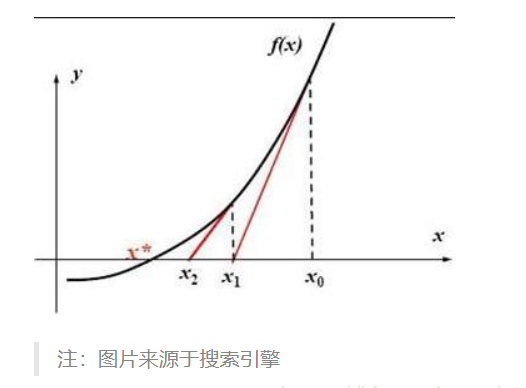
在迭代过程中,以直线代替曲线,用一阶泰勒展式(即在当前点的切线)代替原曲线,求直线与 xx 轴的交点,重复这个过程直到收敛。
首先随便猜一个近似值 xx,然后不断令x等于x和a/x的平均数,迭代个六七次后 xx 的值就已经相当精确了构造方程x − a2 = 0,令f ( x ) = x − a 2 ,然后不断用(x,f(x))的切线来不断逼近方程$x^{2} $
上述函数导数为2x,也就是说函数上任意一点(x,f(x))处的切线斜率为2x。
那么x-f(x)/(2x)就是一个比x更接近的近似值,代入f ( x ) = x 2 − a 可以得到x − ( x2 − a ) / ( 2 x )变形即可得到(x+a/x)/2 这里的a是目标值
二分法
这道题目由于只要求取开平方后的整数部分,因此搜索范围有限,可以考虑使用二分法。
构造数组从0到输入x,该数组中每个元素与其所在位置相等,定义两个指针,左指针left和右指针right,初始位置分别位于数组两端;
执行循环,循环的控制条件是左指针不能跑到右指针的右边去,每轮循环获得中点所在位置,查看该数的平方s与输入x之间的大小关系:
(1)s == x:相当于找到了开方结果,直接返回这个数;
(2)s > x:平方结果较大,删除数组右半部分
(3)s < x:平方结果较小,删除数组左半部分
跳出循环时,返回右指针所在位置。
解决方案
二分查找法应用于搜索平方根的思想很简单,其实就是“猜”,但是是有策略的“猜”,用“排除法”在有限的区间里,一次排除一半的区间元素,最后只剩下一个数,这个数就是题目要求的向下取整的平方根整数。
牛顿法最初提出的时候,是用于求解方程的根,它的基本思想是“以直代曲”,在迭代中搜索得到方程的近似解。
java 实现
实例
public class Solution {public int mySqrt(int x) {if (x == 0) {return 0;}// 注意:针对特殊测试用例,例如 2147395599// 要把搜索的范围设置成长整型long left = 1;long right = x / 2;while (left < right) {// 注意:这里一定取右中位数,如果取左中位数,代码会进入死循环// long mid = left + (right - left + 1) / 2;long mid = (left + right + 1) >>> 1;long square = mid * mid;if (square > x) {right = mid - 1;} else {left = mid;}}// 因为一定存在,因此无需后处理return (int) left;}}
执行结果

python 实现
实例
class Solution(object):def mySqrt(self, x):""":type x: int:rtype: int核心思想:1. 直接return int(sqrt(x)) 直接ac2. 使用暴力遍历方法 for i in range(1,x) 尝试 i*i 是否 == x 或者 i*i < x 但是 (i+1)(i+1) > x3. 使用牛顿法(数值分析中使用到的):在迭代过程中,以直线代替曲线,用一阶泰勒展式(即在当前点的切线)代替原曲线,求直线与 xx 轴的交点,重复这个过程直到收敛。首先随便猜一个近似值 xx,然后不断令x等于x和a/x的平均数,迭代个六七次后 xx 的值就已经相当精确了构造方程x - a^{2} = 0,令f(x)=x-a^{2},然后不断用(x,f(x))的切线来不断逼近方程x^{2}上述函数导数为2x,也就是说函数上任意一点(x,f(x))处的切线斜率为2x。那么x-f(x)/(2x)就是一个比x更接近的近似值,代入f(x)=x^{2}-a可以得到x-(x^{2}-a)/(2x)变形即可得到(x+a/x)/2 这里的a是目标值"""if x == 0:return 0cur_x = x # 令初始值为xwhile cur_x-x/cur_x > 1e-6:cur_x = (cur_x + x/cur_x)/2 # 利用公式(x+a/x)/2计算得到新的areturn int(cur_x)if __name__ == '__main__':s = Solution()print(s.mySqrt(8))相关文章:

【leetcode】leetcode69 x的平方根
文章目录 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。原理牛顿法(数值分析中使用到的):二分法 解决方案java 实现实例执行结果 python 实现实例 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数&…...
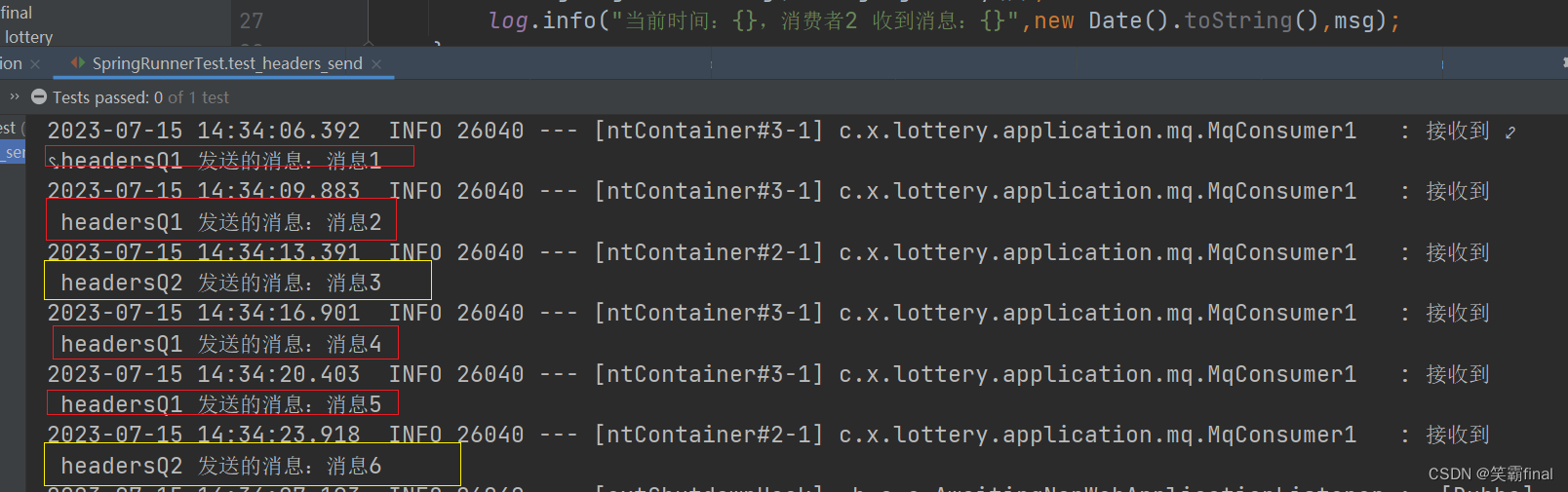
springboot与rabbitmq的整合【演示5种基本交换机】
前言: 👏作者简介:我是笑霸final,一名热爱技术的在校学生。 📝个人主页:个人主页1 || 笑霸final的主页2 📕系列专栏:后端专栏 📧如果文章知识点有错误的地方,…...

【设计模式】设计原则-单一职责原则
单一职责原则 类的设计原则之单一职责原则,是最常用的类的设计的原则之一。 百度百科:就一个类而言,应该仅有一个引起它变化的原因。应该只有一个职责。 通俗的讲就是:一个类只做一件事 这个解释更通俗易懂,也更符…...

【C++】-多态的底层原理
💖作者:小树苗渴望变成参天大树🎈 🎉作者宣言:认真写好每一篇博客💤 🎊作者gitee:gitee✨ 💞作者专栏:C语言,数据结构初阶,Linux,C 动态规划算法🎄 如 果 你 …...
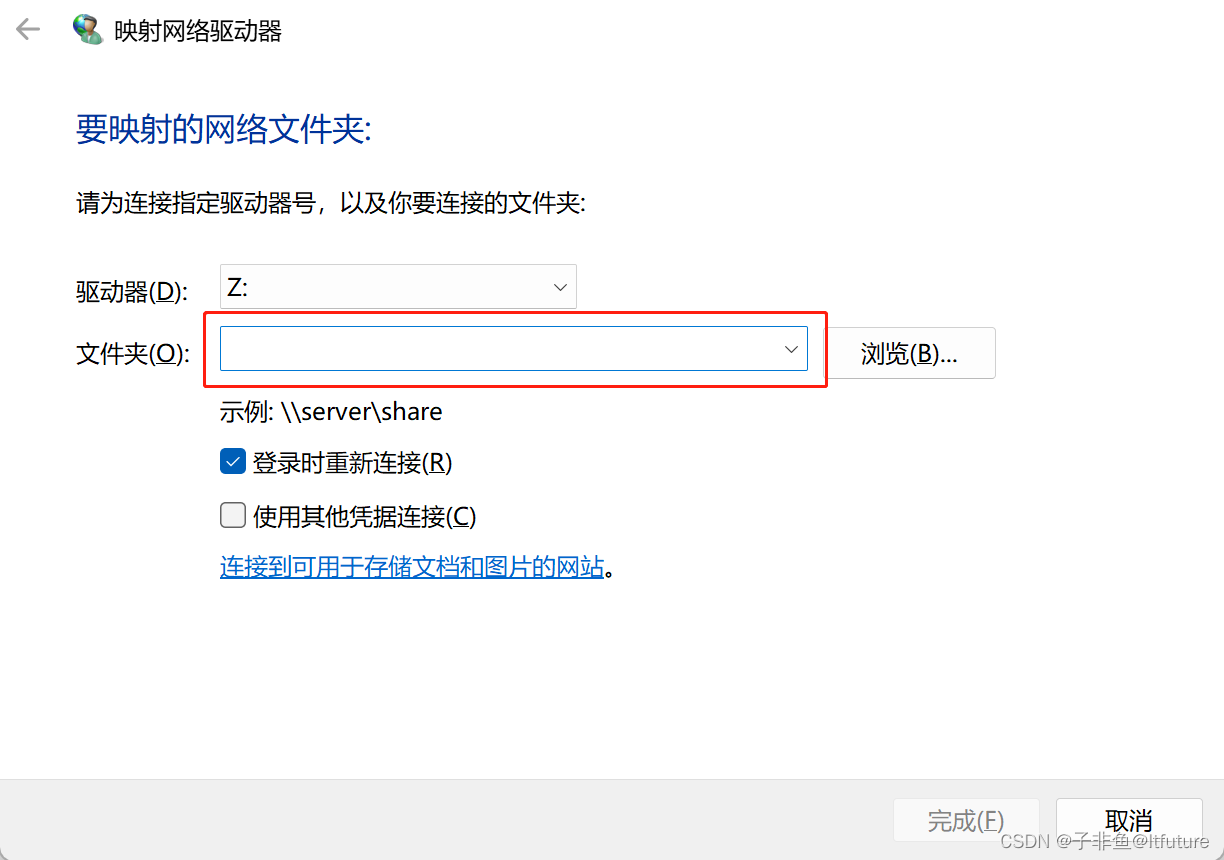
【部署】让你的电脑多出一个磁盘来用!使用SSHFS将远程服务器目录挂载到Windows本地,挂载并共享服务器资源
让你的电脑多出一个磁盘来用!---使用SSHFS将远程服务器目录挂载到Windows本地 1. 方法原理介绍2.SSHFS-Win使用教程—实现远程服务器磁盘挂载本地 由于日常主要用 Windows 系统,每次都得 ssh 到服务器上进行取资源(本地磁盘不富裕)…...
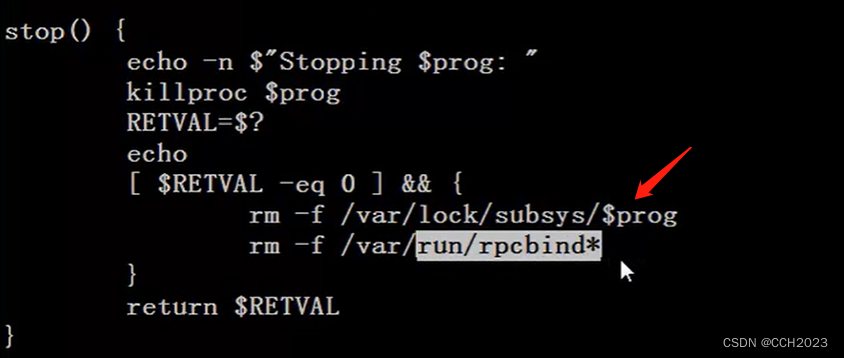
/var/lock/subsys目录的作用
总的来说,系统关闭的过程(发出关闭信号,调用服务自身的进程)中会检查/var/lock/subsys下的文件,逐一关闭每个服务,如果某一运行的服务在/var/lock/subsys下没有相应的选项。在系统关闭的时候,会…...

DETR (DEtection TRansformer)基于自建数据集开发构建目标检测模型超详细教程
目标检测系列的算法模型可以说是五花八门,不同的系列有不同的理论依据,DETR的亮点在于它是完全端到端的第一个目标检测模型,DETR(Detection Transformer)是一种基于Transformer的目标检测模型,由Facebook A…...

C++初阶 - 5.C/C++内存管理
目录 1.C/C的内存分布 2.C语言中动态内存管理方式:malloc、calloc、realloc、free 3.C内存管理方式 3.1 new/delete操作内置类型 3.2 new 和 delete操作自定义类型 4.operator new 与 operator delete 函数(重要点) 4.1 operator new 与…...

数学建模学习(3):综合评价类问题整体解析及分析步骤
一、评价类算法的简介 对物体进行评价,用具体的分值评价它们的优劣 选这两人其中之一当男朋友,你会选谁? 不同维度的权重会产生不同的结果 所以找到每个维度的权重是最核心的问题 0.25 二、评价前的数据处理 供应商ID 可靠性 指标2 指…...
 | 限流:濒临奔溃?限流守护者拯救系统于水火之中!)
【后端面经】微服务构架 (1-5) | 限流:濒临奔溃?限流守护者拯救系统于水火之中!
文章目录 一、前置知识1、什么是限流?2、限流算法A) 静态算法a) 漏桶b) 令牌桶c) 固定窗口d) 滑动窗口B) 动态算法3、限流的模式4、 限流对象4、限流后应该怎么做?二、面试环节1、面试准备2、基本思路3、亮点展现A) 突发流量(针对请求个数而言)B) 请求大小(针对请求大小而言)…...

HDFS异构存储详解
异构存储 HDFS异构存储类型什么是异构存储异构存储类型如何让HDFS知道集群中的数据存储目录是那种类型存储介质 块存储选择策略选择策略说明选择策略的命令 案例:冷热温数据异构存储对应步骤 HDFS内存存储策略支持-- LAZY PERSIST介绍执行使用 HDFS异构存储类型 冷…...

《面试1v1》Kafka消息是采用Pull还是Push模式
🍅 作者简介:王哥,CSDN2022博客总榜Top100🏆、博客专家💪 🍅 技术交流:定期更新Java硬核干货,不定期送书活动 🍅 王哥多年工作总结:Java学习路线总结…...

Windows环境Docker安装
目录 安装Docker Desktop的步骤 Docker Desktop 更新WSL WSL 的手动安装步骤 Windows PowerShell 拉取(Pull)镜像 查看已下载的镜像 输出"Hello Docker!" Docker Desktop是Docker官方提供的用于Windows的图形化桌面应用程序,…...
: singleton类型的bean和prototype类型的bean协同工作的方法(二))
Spring 6.0官方文档示例(23): singleton类型的bean和prototype类型的bean协同工作的方法(二)
使用lookup-method: 一、实体类: package cn.edu.tju.domain2;import java.time.LocalDateTime; import java.util.Map;public class Command {private Map<String, Object> state;public Map<String, Object> getState() {return state;}public void …...
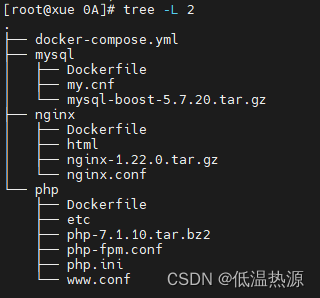
Docker Compose 容器编排
Docker compose Docker compose 实现单机容器集群编排管理(使用一个模板文件定义多个应用容器的启动参数和依赖关系,并使用docker compose来根据这个模板文件的配置来启动容器) 通俗来说就是把之前的多条docker run启动容器命令 转换为docker…...

while循环
while循环是一种常见的循环结构,它会重复执行一段代码,直到指定的条件不再满足。 基本语法如下: while 条件: # 循环体代码 其中,条件是一个布尔表达式,如果为True,则执行循环体中的代码;如果…...

从JVM指令看String对象的比较
在翻看各类 java 知识中,总会提到如下知识:比较 String 对象,例如: String a1new String("10"); String a2"10"; String a3"1""0";//结果 System.out.println(a1a2); //false System.ou…...
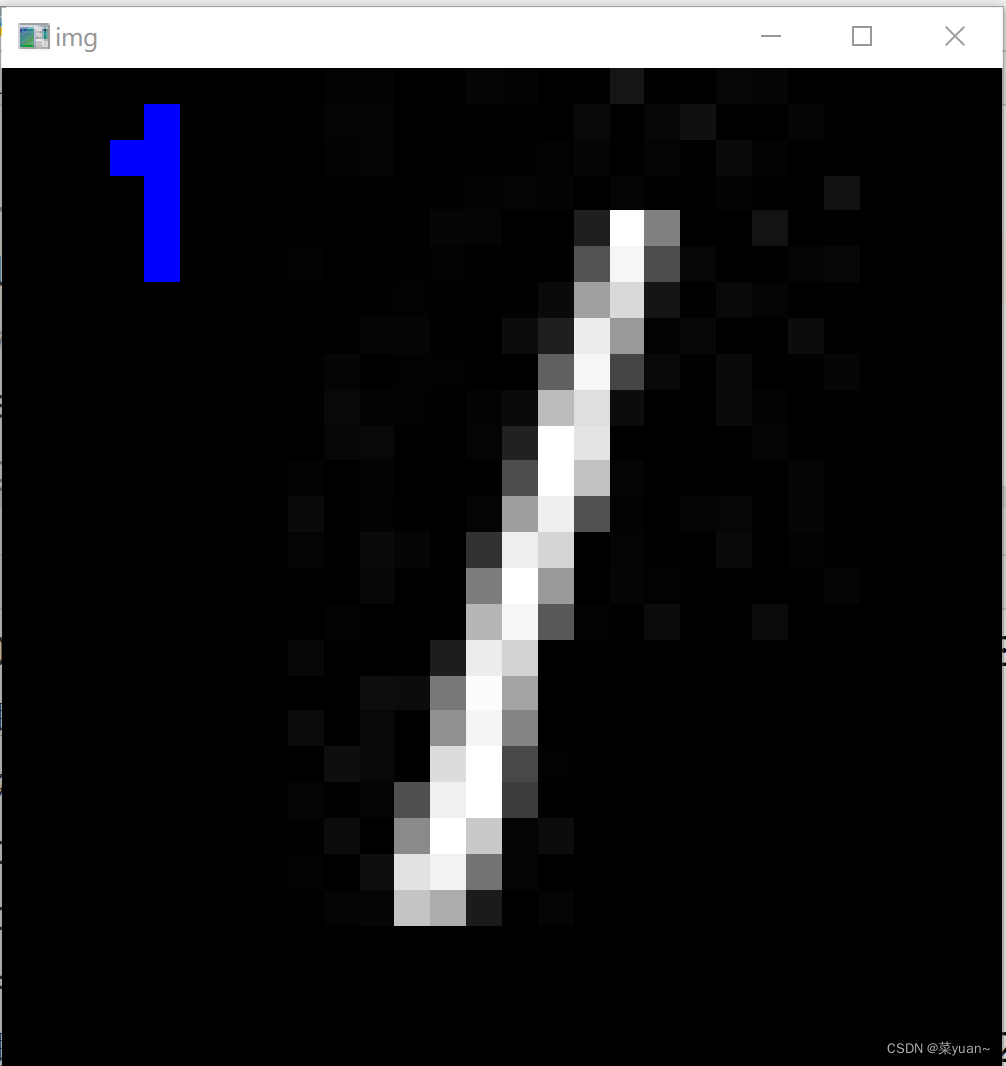
python与深度学习(六):CNN和手写数字识别二
目录 1. 说明2. 手写数字识别的CNN模型测试2.1 导入相关库2.2 加载数据和模型2.3 设置保存图片的路径2.4 加载图片2.5 图片预处理2.6 对图片进行预测2.7 显示图片 3. 完整代码和显示结果4. 多张图片进行测试的完整代码以及结果 1. 说明 本篇文章是对上篇文章训练的模型进行测试…...
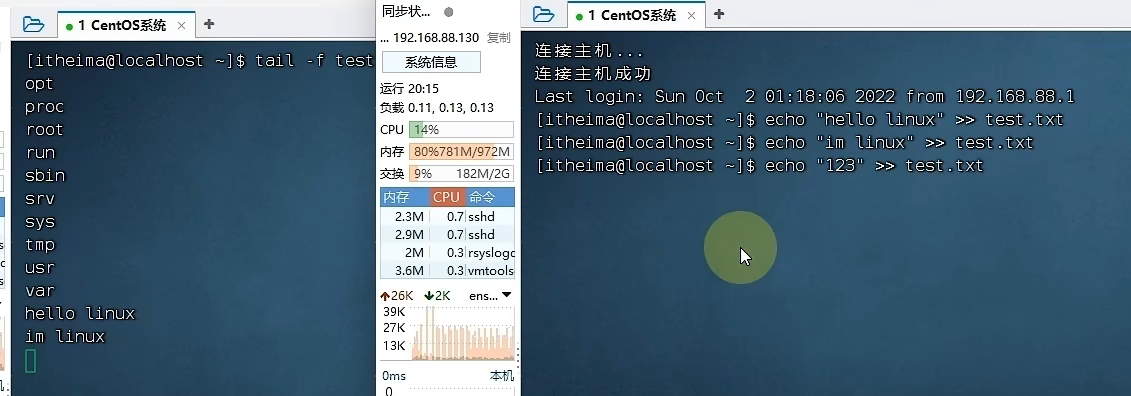
Linux使用教程
一、Linux命令基础 1、ls、ll命令——展示数据 ①ls命令——平铺展示数据 其中ls命令以平铺的方式展现数据 ②ll命令——列表展示数据 ll命令以列表的方式展现数据 -a选项,表示:all的意思,即列出全部文件(包含隐藏的文件/文件夹…...

项目名称:智能家居边缘网关项目
一,项目介绍 软件环境: C语言 硬件环境: STM32G030C8TX单片机开发板 开发工具: Linux平台GCC交叉编译环境以及ukeil (1)边缘网关概念 边缘网关是部署在网络边缘侧的网关,通过网络联接、协议转换等功能联接物理和数字世界,提供轻量化的联接管…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
