什么是SVM算法?硬间隔和软间隔的分类问题
SVM全称是supported vector machine(支持向量机),即寻找到一个超平面使样本分成两类,并且间隔最大。
SVM能够执行线性或⾮线性分类、回归,甚至是异常值检测任务。它是机器学习领域最受欢迎的模型之一。SVM特别适用于中小型复杂数据集的分类。
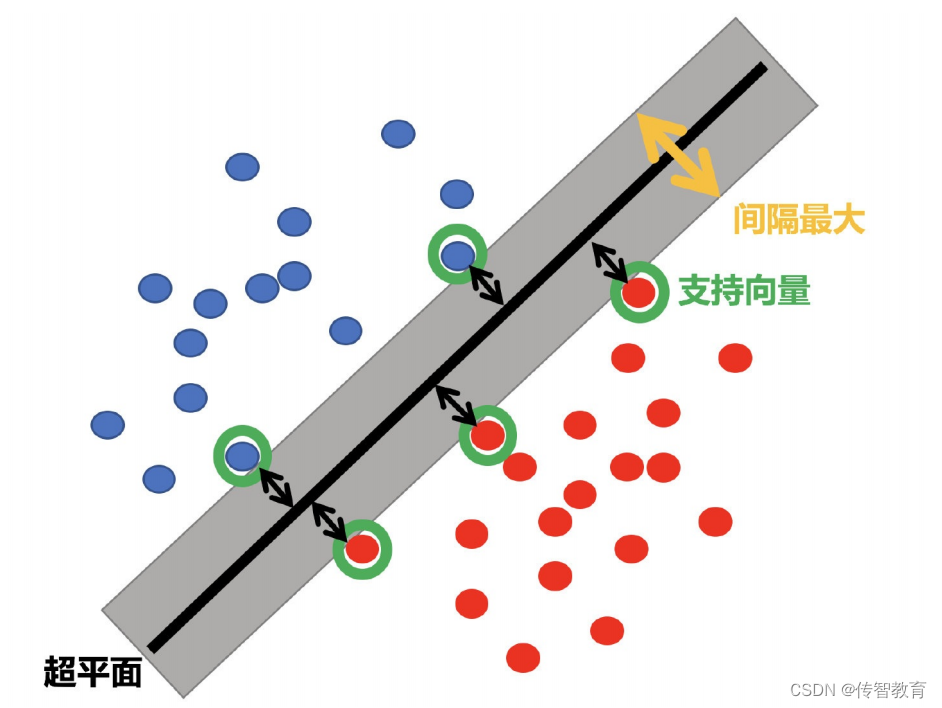
超平面最大间隔

上左图显示了三种可能的线性分类器的决策边界:虚线所代表的模型表现非常糟糕,甚至都无法正确实现分类。其余两个模型在这个训练集上表现堪称完美,但是它们的决策边界与实例过于接近,导致在面对新实例时,表现可能不会太好。
右图中的实线代表SVM分类器的决策边界,不仅分离了两个类别,且尽可能远离最近的训练实例。
硬间隔分类
在上面我们使用超平面进行分割数据的过程中,如果我们严格地让所有实例都不在最大=大间隔之间,并且位于正确的一边,这就是硬间隔分类。
硬间隔分类有两个问题,首先,它只在数据是线性可分离的时候才有效;其次,它对异常值非常敏感。
当有一个额外异常值的鸢尾花数据:左图的数据根本找不出硬间隔,而右图最终显示的决策边界与我们之前所看到的无异常值时的决策边界也大不相同,可能无法很好地泛化。
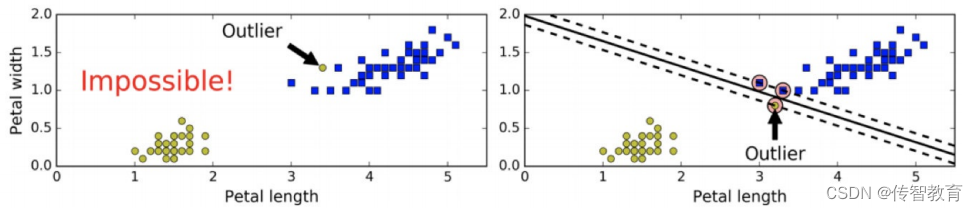
软间隔分类
要避免这些问题,最好使用更灵活的模型。目标是尽可能在保持最大间隔宽阔和限制间隔违例(即位于最大间隔之上,甚至在错误的一边的实例)之间找到良好的平衡,这就是软间隔分类。
要避免这些问题,最好使用更灵活的模型。目标是尽可能在保持间隔宽阔和限制间隔违例之间找到良好的平衡,这就是软间隔分类。
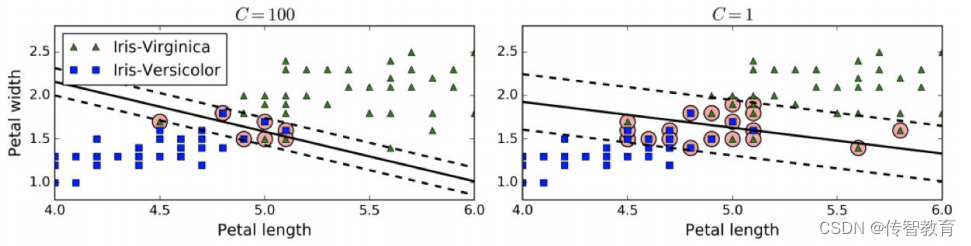
在Scikit-Learn的SVM类中,可以通过超参数C来控制这个平衡:C值越小,则间隔越宽,但是间隔违例也会越多。上图 显示了在一个非线性可分离数据集上,两个软间隔SVM分类器各自的决策边界和间隔。
左边使用了高C值,分类器的错误样本(间隔违例)较少,但是间隔也较小。
右边使用了低C值,间隔大了很多,但是位于间隔上的实例也更多。看起来第二个分类器的泛化效果更好,因为大多数间隔违例实际上都位于决策边界正确的一边,所以即便是在该训练集上,它做出的错误预测也会更少。
相关文章:

什么是SVM算法?硬间隔和软间隔的分类问题
SVM全称是supported vector machine(支持向量机),即寻找到一个超平面使样本分成两类,并且间隔最大。 SVM能够执行线性或⾮线性分类、回归,甚至是异常值检测任务。它是机器学习领域最受欢迎的模型之一。SVM特别适用于中小型复杂数据集的分类。…...

Normalization(BN and LN) in NN
Batch Normalization 称为批标准化。批是指一批数据,通常为 mini-batch;标准化是处理后的数据服从 N ( 0 , 1 ) N(0,1) N(0,1) 的正态分布。在训练过程中,数据需要经过多层的网络,如果数据在前向传播的过程中,尺度发…...
opencv-22 图像几何变换01-缩放-cv2.resize()(图像增强,图像变形,图像拼接)
什么是几何变换? 几何变换是计算机图形学中的一种图像处理技术,用于对图像进行空间上的变换,而不改变图像的内容。这些变换可以通过对图像中的像素位置进行调整来实现。 常见的几何变换包括: 平移(Translation&#x…...

python机器学习(五)逻辑回归、决策边界、代价函数、梯度下降法实现线性和非线性逻辑回归
线性回归所解决的问题是把数据集的特征传入到模型中,预测一个值使得误差最小,预测值无限接近于真实值。比如把房子的其他特征传入到模型中,预测出房价, 房价是一系列连续的数值,线性回归解决的是有监督的学习。有很多场…...
, AsQueryable() ,.ToList(),的区别和用法)
聊聊Linq中.AsEnumerable(), AsQueryable() ,.ToList(),的区别和用法
聊聊Linq中.AsEnumerable(), AsQueryable() ,.ToList(),的区别和用法 当使用LINQ查询数据时,我们常常会面临选择使用.AsEnumerable(), .AsQueryable(), 和 .ToList()方法的情况。这些方法在使用时有不同的效果和影响,需要根据具体场景来选择合适的方法。…...

【机器学习】机器学习中的“本体”概念
一、说明 在机器学习中,本体越来越多地用于提供基于相似性分析和场景知识的 ML 模型。 在传统的基于标签的定义中,对象往往是孤立的,可扩展性差,存在重复的可能性,对象之间的关系无法体现。在基于本体的定义中…...

ChatGPT是否能够进行对话中的参考和指代解析?
ChatGPT在对话中的参考和指代解析方面有一定的潜力,但需要针对具体任务和上下文进行定制和优化。参考和指代解析是指理解对话中的代词、名词短语等表达方式所指代的具体对象或信息。在对话中,参考和指代解析对于理解上下文、保持对话连贯性和生成准确回复…...
网红项目AutoGPT源码内幕及综合案例实战(三)
AutoGPT on LangChain PromptGenerator等源码解析 本节阅读AutoGPT 的prompt_generator.py源代码,其中定义了一个PromptGenerator类和一个get_prompt函数,用于生成一个提示词信息。PromptGenerator类提供了添加约束、命令、资源和性能评估等内容的方法,_generate_numbered_l…...

第八章:list类
系列文章目录 文章目录 系列文章目录前言list的介绍及使用list的介绍list的使用list的构造函数list的迭代器list的容量list的成员访问list的增删改查 list与vector的对比总结 前言 list是STL的一种链表类,可以在常数范围内在任意位置进行插入和删除的序列式容器。 …...

VUE声音-报警-实现方式
1.先准备一个mp3文件包:(这个24小时生效如果失效可留言,看到就会增加时效) 获取mp3地址: https://www.aliyundrive.com/t/uQ8zqjn9JKSfm7QlGOSr2.代码内容 进入页面就会自动 播放mp3的内容信息了。 <template>…...

【Coppeliasim C++】焊接机械臂仿真
项目思维导图 该项目一共三个demo: 机械臂末端走直线 2. 变位机转台转动 3.机械臂末端多点样条运动 笔记: 基于等级的蚁群系统在3D网格地图中搜索路径的方法: 基于等级的蚁群系统(Hierarchical Ant Colony System,HACS)是一种改进的蚁群优化算法。它在传…...

【LeetCode】94.二叉树的中序遍历
题目 给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。 示例 1: 输入:root [1,null,2,3] 输出:[1,3,2]示例 2: 输入:root [] 输出:[]示例 3: 输入:root [1] 输…...
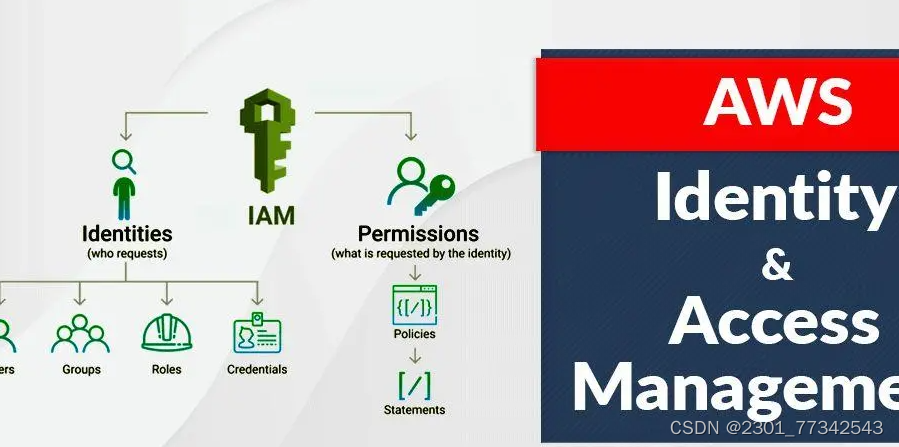
AWS IAM介绍
前言 AWS是世界上最大的云服务提供商,它提供了很多组件供消费者使用,其中进行访问控制的组件叫做IAM(Identity and Access Management), 用来进行身份验证和对AWS资源的访问控制。 功能 IAM的功能总结来看,主要分两种࿱…...
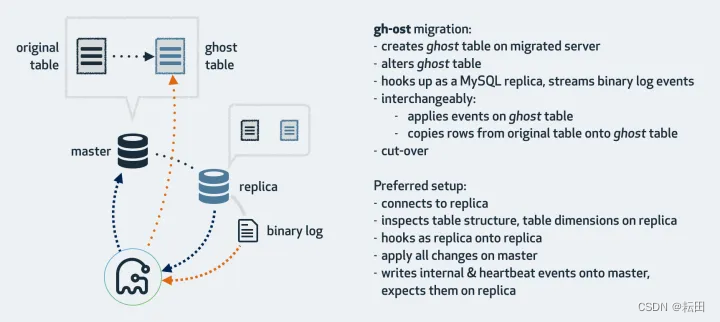
MySQL碎片清理
为什么产生? 经过大量增删改的表,都可能存在碎片 MySQL数据结构是B树, 删除某一记录,只会标记为删除,后续插入一条该区间的记录,就会复用这个位置。 删除整个数据页的记录,则整个页标记为“可…...

elasticsearch操作(API方式)
说明:es操作索引库、文档,除了使用它们自带的命令外(参考:http://t.csdn.cn/4zpmi),在IDEA中可以添加相关的依赖,使用对应的API来操作。 准备工作 搭建一个SpringBoot项目,DAO使用…...

Vue2.0 使用 echarts
目录 1. 配置 渲染2. 数据渲染 1. 配置 渲染 安装 echarts 依赖 npm install echarts -Smain.js,引入 echarts import * as echarts from echarts// 在import的后面,echarts的前面加一个 * as Vue.prototype.$echarts echarts从 echarts 官网直接复制…...

企业微信,阿里钉钉告警群机器人
链接:如何通过企业微信群接收报警通知_云监控-阿里云帮助中心...

linux下的tomcat
springboot项目端口是8080,部署到linux运行之后,为什么能检测到tomcat 手动安装tomcat,以下是在 Linux 系统上安装 Tomcat 的步骤: 下载 Tomcat 安装包。您可以从 Tomcat 官方网站(https://tomcat.apache.org/ ↗&…...

Vue源码学习 - new Vue初始化都做了什么?
目录 前言一、创建一个 Vue 实例二、找到 Vue 构造函数三、源码分析 - Vue.prototype._init四、源码分析 - 调用 $mount 方法,进入挂载阶段五、总结 前言 使用Vue也有一段时间了,最近去阅读了Vue的源码,想总结分享下学到的新东西。 如果觉得…...
新零售数字化商业模式如何建立?新零售数字化营销怎么做?
随着零售行业增速放缓、用户消费结构升级,企业需要需求新的价值增长点进行转型升级,从而为消费者提供更为多元化的消费需求、提升自己的消费体验。在大数据、物联网、5G及区块链等技术兴起的背景下,数字化新零售系统应运而生。 开利网络认为&…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
