ICP算法和优化问题详细公式推导
1. 介绍
ICP(Iterative Closest Point):求一组平移和旋转使得两个点云之间重合度尽可能高。
2. 算法流程
找最近邻关联点,求解 R , t R , t R , t R , t R,tR,tR,tR,t R,tR,tR,tR,t,如此反复直到重合程度足够高。
3. 数学描述
X = { x 1 , x 2 , . . . , x N x } X=\left\{ {x_1,x_2,...,x_{Nx} }\right\} X={x1,x2,...,xNx}
Y = { y 1 , y 2 , . . . , y N y } Y=\left\{ {y_1,y_2,...,y_{Ny} } \right\} Y={y1,y2,...,yNy}
由于是变换前后对应点云,则 N x = N y Nx=Ny Nx=Ny
min E ( R , t ) = min ∑ i = 1 N x ∥ y i − ( R x i + t ) ∥ 2 \min E(R,t) = \min \sum\nolimits_{i = 1}^{Nx} {{{\left\| {{y_i} - \left( {R{x_i} + t} \right)} \right\|}^2}} minE(R,t)=min∑i=1Nx∥yi−(Rxi+t)∥2
求解使其最小的 R , t R,t R,t
4. 解法
4.1 SVD直接解法
min E ( R , t ) = min ∑ i = 1 N x ∥ y i − ( R x i + t ) ∥ 2 = min ∑ i = 1 N x ∥ y i − R x i − t − μ y + R μ x + μ y − R μ x ∥ 2 \begin{aligned} \min E(R,t) &= \min \sum\nolimits_{i = 1}^{Nx} {{{\left\| {{y_i} - \left( {R{x_i} + t} \right)} \right\|}^2}} \\ &= \min \sum\nolimits_{i = 1}^{Nx} {{{\left\| {{y_i} - R{x_i} - t - {\mu _y} + R{\mu _x} + {\mu _y} - R{\mu _x}} \right\|}^2}} \end{aligned} minE(R,t)=min∑i=1Nx∥yi−(Rxi+t)∥2=min∑i=1Nx∥yi−Rxi−t−μy+Rμx+μy−Rμx∥2
其中
μ x = ∑ i = 1 N x x i , μ y = ∑ i = 1 N y y i \mu _x = \sum\nolimits{i = 1}^{Nx} {x_i} ,\mu _y = \sum\nolimits_{i = 1}^{Ny} {y_i} μx=∑i=1Nxxi,μy=∑i=1Nyyi
则
min E ( R , t ) = min ∑ i = 1 N x ∥ y i − R x i − t − μ y + R μ x + μ y − R μ x ∥ 2 = min ∑ i = 1 N x ∥ y i − μ y − R ( x i − μ x ) + μ y − R μ x − t ∥ 2 = min ∑ i = 1 N x ( ∥ y i − μ y − R ( x i − μ x ) ∥ 2 + ∥ μ y − R μ x − t ∥ 2 + 2 [ y i − μ y − R ( x i − μ x ) ] T ( μ y − R μ x − t ) ) \begin{aligned} \min E(R,t) &=\min \sum\nolimits_{i = 1}^{Nx} {{{\left\| {{y_i} - R{x_i} - t - {\mu _y} + R{\mu _x} + {\mu _y} - R{\mu _x}} \right\|}^2}} \\ &=\min \sum\nolimits_{i = 1}^{Nx} {\left\| {y_i-\mu_y-R(x_i-\mu_x)+\mu_y-R\mu_x-t}\right\|}^2 \\ &=\min \sum\nolimits_{i = 1}^{Nx} ({\left\| {y_i-\mu_y-R(x_i-\mu_x)} \right\|}^2 +{\left\|{\mu_y-R\mu_x-t}\right\|}^2 \\ &+2[y_i-\mu_y-R(x_i-\mu_x)]^T(\mu_y-R\mu_x-t)) \end{aligned} minE(R,t)=min∑i=1Nx∥yi−Rxi−t−μy+Rμx+μy−Rμx∥2=min∑i=1Nx∥yi−μy−R(xi−μx)+μy−Rμx−t∥2=min∑i=1Nx(∥yi−μy−R(xi−μx)∥2+∥μy−Rμx−t∥2+2[yi−μy−R(xi−μx)]T(μy−Rμx−t))
其中 ∑ i = 1 N x x i − N x μ x = 0 , ∑ i = 1 N y y i − N y μ y = 0 \sum\nolimits_{i = 1}^{Nx}x_i-Nx\mu_x=0 ,\sum\nolimits_{i = 1}^{Ny}y_i-Ny\mu_y=0 ∑i=1Nxxi−Nxμx=0,∑i=1Nyyi−Nyμy=0
min E ( R , t ) = min ∑ i = 1 N x ( ∥ y i − μ y − R ( x i − μ x ) ∥ 2 + ∥ μ y − R μ x − t ∥ 2 ) \min E(R,t) =\min \sum\nolimits_{i = 1}^{Nx} ({\left\| {y_i-\mu_y-R(x_i-\mu_x)} \right\|}^2 +{\left\|{\mu_y-R\mu_x-t}\right\|}^2) minE(R,t)=min∑i=1Nx(∥yi−μy−R(xi−μx)∥2+∥μy−Rμx−t∥2)
这样第一项中只含有变量 R R R,第二项含有 R , t R,t R,t,求整体的最小值可以使第一项的值最小,将得到的 R R R,带入第二项中,再使第二项为零求出 t t t的值。
min ∑ i = 1 N x ∥ y i − μ y − R ( x i − μ x ) ∥ 2 = min ∑ i = 1 N x ∥ y i ′ − R x i ′ ∥ 2 = min ∑ i = 1 N x ( y i ′ − R x i ′ ) T ( y i ′ − R x i ′ ) = min ∑ i = 1 N x ∥ y i ′ ∥ 2 + x i ′ T R T R x i ′ − x i ′ T R T y i ′ − y i ′ T R x i ′ = min ∑ i = 1 N x ∥ y i ′ ∥ 2 + x i ′ T R T R x i ′ − 2 x i ′ T R T y i ′ \begin{aligned} \min \sum\nolimits_{i = 1}^{Nx} &{\left\| {y_i-\mu_y-R(x_i-\mu_x)} \right\|}^2=\min \sum\nolimits_{i = 1}^{Nx} {\left\| {y_i'-Rx_i'} \right\|}^2 \\ &=\min \sum\nolimits_{i = 1}^{Nx} {(y_i'-Rx_i')^T(y_i'-Rx_i')} \\ &=\min \sum\nolimits_{i = 1}^{Nx} {\left\| y_i' \right\|}^2+x_i'^TR^TRx_i'-x_i'^TR^Ty_i'-y_i'^TRx_i' \\ &=\min \sum\nolimits_{i = 1}^{Nx} {\left\| y_i' \right\|}^2+x_i'^TR^TRx_i'-2x_i'^TR^Ty_i' \end{aligned} min∑i=1Nx∥yi−μy−R(xi−μx)∥2=min∑i=1Nx∥yi′−Rxi′∥2=min∑i=1Nx(yi′−Rxi′)T(yi′−Rxi′)=min∑i=1Nx∥yi′∥2+xi′TRTRxi′−xi′TRTyi′−yi′TRxi′=min∑i=1Nx∥yi′∥2+xi′TRTRxi′−2xi′TRTyi′
求解原函数最小值等同于求解: min ∑ i = 1 N x − x i ′ T R T y i ′ \min \sum\nolimits_{i = 1}^{Nx}{-x_i'^TR^Ty_i'} min∑i=1Nx−xi′TRTyi′
等同于求解: max ∑ i = 1 N x x i ′ T R T y i ′ \max \sum\nolimits_{i = 1}^{Nx}{x_i'^TR^Ty_i'} max∑i=1Nxxi′TRTyi′
max ∑ i = 1 N x x i ′ T R T y i ′ = max T r a c e ( ∑ i = 1 N x R x i ′ y i ′ T ) = max T r a c e ( R H ) \max \sum\nolimits_{i = 1}^{Nx}{x_i'^TR^Ty_i'}=\max Trace\left( {\sum\nolimits_{i = 1}^{Nx}{Rx_i'y_i'^T}} \right)=\max Trace(RH) max∑i=1Nxxi′TRTyi′=maxTrace(∑i=1NxRxi′yi′T)=maxTrace(RH)
由定理可知对于正定矩阵 A A T AA^T AAT和任意正交矩阵 B B B,有: T r ( A A T ) ≥ T r ( B A A T ) Tr(AA^T) \ge Tr(BAA^T) Tr(AAT)≥Tr(BAAT)
则对矩阵 H H H进行SVD分解:
H = U Σ V T H=U\Sigma V^T H=UΣVT
取 R = V U T R=VU^T R=VUT,则由定理得到此时的 R R R使得原式最大
再对应求解: t = μ y − R μ x t=\mu_y-R\mu_x t=μy−Rμx
4.2 迭代求解
将ICP构建成一个优化问题
F ( x ) = ∑ i = 1 n ∥ x i − T y i ∥ 2 2 F(x)=\sum\nolimits_{i = 1}^{n}{\left\| x_i-Ty_i \right\|}_2^2 F(x)=∑i=1n∥xi−Tyi∥22
其中 T T T为位姿变换矩阵
T = [ R t 0 1 ] T = {\begin{bmatrix} R&{\rm{t}}\\ 0&1 \end{bmatrix}} T=[R0t1]
求解优化问题需要构建残差约束并计算雅可比矩阵,这里的残差为 x i − T y i x_i-Ty_i xi−Tyi(可以理解为为变换后的点云与目标待配准点云之间的差异),计算雅可比矩阵可以使用李代数的方法对目标函数求导。
5.(非线性优化问题详细公式推导)
问题描述:
对于一个目标函数 F ( X ) = ∥ f ( X ) ∥ 2 F(X)= {\left\| f(X) \right\|}^2 F(X)=∥f(X)∥2,其中 F : R n → R m , X ∈ R n F:\mathbb{R}^n \to \mathbb{R}^m ,X \in \mathbb{R}^n F:Rn→Rm,X∈Rn ,需要求解 X X X使得目标函数 F ( X ) F(X) F(X) 取值最小。如果 f ( X ) f(X) f(X)为线性函数,则可以简化为最小二乘问题,可以求得最优解,但 f ( X ) f(X) f(X)为非线性函数则无法直接求解,需要迭代求解。
F ( X + Δ X ) = ∥ f ( X + Δ X ) ∥ 2 F(X+\Delta X)= {\left\| f(X+\Delta X) \right\|}^2 F(X+ΔX)=∥f(X+ΔX)∥2
迭代求 Δ X \Delta X ΔX使得 F ( X + Δ X ) F(X+\Delta X) F(X+ΔX)减小,直到其足够小并接近最小值时停止。
那么 Δ X \Delta X ΔX的取值该如何确定?
1. 高斯法
对 F ( X + Δ X ) F(X+\Delta X) F(X+ΔX)进行Taylor Expansion得到:
F ( X + Δ X ) = F ( X ) + J F Δ X + 1 2 Δ X T H F Δ X + O ( Δ X ) F(X+\Delta X)=F(X)+J_F\Delta X+\frac{1}{2}\Delta X^TH_F\Delta X+O(\Delta X) F(X+ΔX)=F(X)+JFΔX+21ΔXTHFΔX+O(ΔX)
只取到二阶项,其中 J J J为 F F F的雅可比矩阵, H H H为海塞矩阵, O ( Δ X ) O(\Delta X) O(ΔX)为忽略的高阶项。
雅可比矩阵定义:
有矩阵函数 F ( X ) F(X) F(X),其中 F : R n → R m , X ∈ R n F:\mathbb{R}^n \to \mathbb{R}^m ,X \in \mathbb{R}^n F:Rn→Rm,X∈Rn
J F = ∂ F ( X ) ∂ X T J_F=\frac{\partial F(X)}{\partial X^T} JF=∂XT∂F(X)
使等式对 Δ X \Delta X ΔX求导为 0 0 0得到:
∂ F ( X + Δ X ) ∂ Δ X = J F + H F Δ X = 0 \frac{\partial F(X+\Delta X)}{\partial \Delta X}=J_F+H_F\Delta X=0 ∂ΔX∂F(X+ΔX)=JF+HFΔX=0
由此得到 Δ X \Delta X ΔX的取值。
2. 高斯-牛顿法
F ( X + Δ X ) = ∥ f ( X + Δ X ) ∥ 2 F(X+\Delta X)= {\left\| f(X+\Delta X) \right\|}^2 F(X+ΔX)=∥f(X+ΔX)∥2
对 f ( X + Δ X ) f(X+\Delta X) f(X+ΔX)进行Taylor Expansion得到:
f ( X + Δ X ) = f ( X ) + J f Δ X + O ( Δ X ) f(X+\Delta X)=f(X)+J_f\Delta X+O(\Delta X) f(X+ΔX)=f(X)+JfΔX+O(ΔX)
只取到一阶项。
F ( X + Δ X ) = ∥ f ( X + Δ X ) ∥ 2 = ( f ( X ) + J f Δ X ) T ( f ( X ) + J f Δ X ) = ∥ f ( X ) ∥ 2 + Δ X T J f T J f Δ X + Δ X T J f T f ( X ) + f ( X ) T J f Δ X = ∥ f ( X ) ∥ 2 + Δ X T J f T J f Δ X + 2 f ( X ) T J f Δ X \begin{aligned} F(X+\Delta X) &= {\left\| f(X+\Delta X) \right\|}^2 \\ &= (f(X)+J_f\Delta X)^T(f(X)+J_f\Delta X) \\ &={\left\| f(X) \right\|}^2+\Delta X^TJ_f^TJ_f\Delta X+\Delta X^TJ_f^Tf(X)+f(X)^TJ_f\Delta X \\ &={\left\| f(X) \right\|}^2+\Delta X^TJ_f^TJ_f\Delta X+2f(X)^TJ_f\Delta X \end{aligned} F(X+ΔX)=∥f(X+ΔX)∥2=(f(X)+JfΔX)T(f(X)+JfΔX)=∥f(X)∥2+ΔXTJfTJfΔX+ΔXTJfTf(X)+f(X)TJfΔX=∥f(X)∥2+ΔXTJfTJfΔX+2f(X)TJfΔX
使等式对 Δ X \Delta X ΔX求导等于 0 0 0得到:
∂ F ( X + Δ X ) ∂ Δ X = 2 J f T J f Δ X + 2 f ( X ) T J f = 0 \frac{\partial F(X+\Delta X)}{\partial \Delta X}=2J_f^TJ_f\Delta X+2f(X)^TJ_f=0 ∂ΔX∂F(X+ΔX)=2JfTJfΔX+2f(X)TJf=0
可以求得
J f T J f Δ X = − f ( X ) T J f J_f^TJ_f\Delta X=-f(X)^TJ_f JfTJfΔX=−f(X)TJf
相关文章:

ICP算法和优化问题详细公式推导
1. 介绍 ICP(Iterative Closest Point):求一组平移和旋转使得两个点云之间重合度尽可能高。 2. 算法流程 找最近邻关联点,求解 R , t R , t R , t R , t R,tR,tR,tR,t R,tR,tR,tR,t,如此反复直到重合程度足够高。 3. 数学描述 X { x 1 ,…...
【安全狗】linux免费服务器防护软件安全狗详细安装教程
在费用有限的基础上,复杂密码云服务器基础防护常见端口替换安全软件,可以防护绝大多数攻击 第一步:下载服务器安全狗Linux版(下文以64位版本为例) 官方提供了两个下载方式,本文采用的是 方式2 wget安装 方…...

【iOS】自定义字体
文章目录 前言一、下载字体二、添加字体三、检查字体四、使用字体 前言 在设计App的过程中我们常常会想办法去让我们的界面变得美观,使用好看的字体是我们美化界面的一个方法。接下来笔者将会讲解App中添加自定义字体 一、下载字体 我们要使用自定义字体&#x…...

WPF实战学习笔记06-设置待办事项界面
设置待办事项界面 创建待办待办事项集合并初始化 TodoViewModel: using Mytodo.Common.Models; using Prism.Commands; using Prism.Mvvm; using System; using System.Collections.Generic; using System.Collections.ObjectModel; using System.Linq; using Sy…...

推荐几个不错的免费配色工具网站
1. Paletton专业的配色套件,提供色轮理论及调色功能。可查看配色预览效果。 网站:http://paletton.com 2. Colormind一个基于机器学习的智能配色工具。可以一键生成配色方案。 网站:http://colormind.io 3. Adobe ColorAdobe官方的配色工具,可以从图片中取色,也可以随机生成配色…...

gitee page发布的静态网站,无法播放目录中的mp4视频
起因是希望在gitee上部署静态网站,利用three.js VideoTexture 环境贴图播放视频。 但是试了多几次 mp4均提示404,资源无法获取; 找了很多方案,最后发现将视频转为ogv 就可以完美适配了; mp4转ogv 附threejs使用ogv进…...

opencv-26 图像几何变换04- 重映射-函数 cv2.remap()
什么是重映射? 重映射(Remapping)是图像处理中的一种操作,用于将图像中的像素从一个位置映射到另一个位置。重映射可以实现图像的平移、旋转、缩放和透视变换等效果。它是一种基于像素级的图像变换技术,可以通过定义映…...
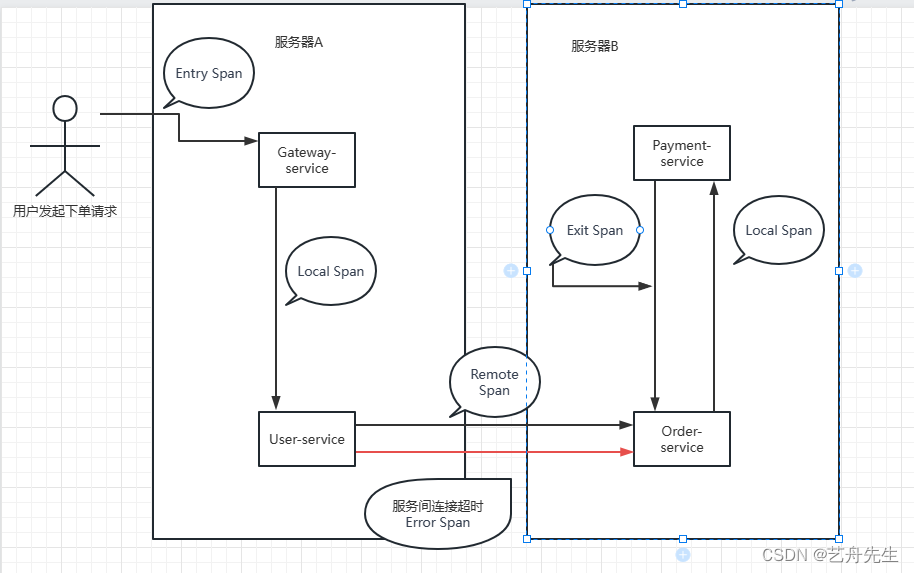
SkyWalking链路追踪中span全解
基本概念 在SkyWalking链路追踪中,Span(跨度)是Trace(追踪)的组成部分之一。Span代表一次调用或操作的单个组件,可以是一个方法调用、一个HTTP请求或者其他类型的操作。 每个Span都包含了一些关键的信息&am…...
——Redux的简介)
【前端知识】React 基础巩固(三十一)——Redux的简介
React 基础巩固(三十一)——Redux 一、Redux是个纯函数 概念 纯函数(确定的输入一定产生确定的输出,函数在执行过程中不产生副作用): 在程序设计中,若一个函数符合以下条件,那么这个函数就被称为纯函数…...

拦截Bean使用之前各个时机的Spring组件
拦截Bean使用之前各个时机的Spring组件 之前使用过的BeanPostProcessor就是在Bean实例化之后,注入属性值之前的时机。 Spring Bean的生命周期本次演示的是在Bean实例化之前的时机,使用BeanFactoryPostProcessor进行验证,以及在加载Bean之前进…...
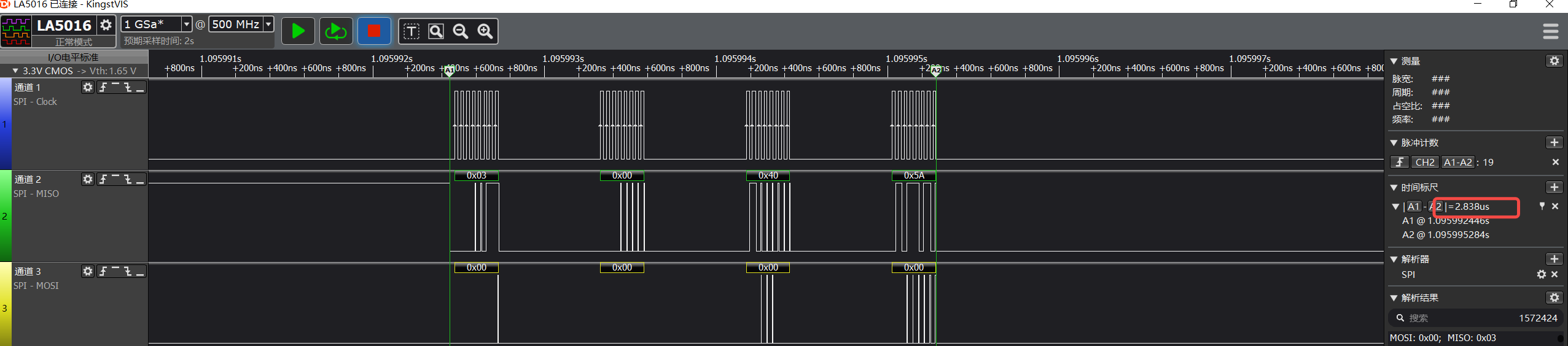
RT thread 之 Nand flash 读写过程分析
文章目录 前言:什么是Nand Flash?1、Nand Flash 读取步骤2、从主存读到Cache2.1 在标准spi接口下读取过程2.2 测试时序(SPI频率30MHz) 3.从Cache读取数据3.1在标准spi接口读取过程测试时序 前言:什么是Nand Flash&…...

独立站最全出单营销指南,新手卖家赶紧学起来吧!
这是一个需要投入大量时间和精力的挑战,但只有经过筛选在众多品牌和渠道中找到最适合自己的营销策略,才能成功。 新手商家经常会发现自己有很多可以改进的地方:品牌的颜色、字体以及其他一些细节。但真正走向成熟的商家会意识到,…...
Git移除commit过的大文件
前言:在提交推送本地更改至仓库时,误将大文件给提交了,导致push时报错文件过大,因此需要将已经commit的大文件移除后再push 若已知要删除的文件或文件夹路径,则可以从第4步开始 1.对仓库进行gc操作 $ git gc 2.查询…...

再见 Spring Boot 1.X ,Spring Boot 2.X 走向舞台中心
2019年8月6日,Spring 官方在其博客宣布,Spring Boot 1.x 停止维护,Spring Boot 1.x 生命周期正式结束。 其实早在2018年7月30号,Spring 官方就已经在博客进行过预告,Spring Boot 1.X 将维护到2019年8月1日。 1.5.x 将会…...

Jsonp劫持
JSONP 介绍 jsonp是一种协议,准确的说,他是json的一种使用模式,为了解决Json受同源策略限制的问题。 基本语法 JSONP的基本语法为:callback({“name”:”test”, “msg”:”success”}) 常见的例子包括函数调用(如…...
STM32CubeIDE(串口)
目录 一、轮询模式 1.1 配置USART2为异步模式 1.2 500ms发送一次消息 1.3 通信结果 1.4 串口控制LED 二、中断收发 2.1 开启中断 2.2 中断发送接收 2.2.1 中断发送只需要调用接口 2.2.2 中断接收 2.3 实验结果 三、DMA模式与收发不定长数据 3.1 DMA通道配置 3.2 DMA…...

Python编程很简单,四步菜鸟到高手(文末送书5本)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
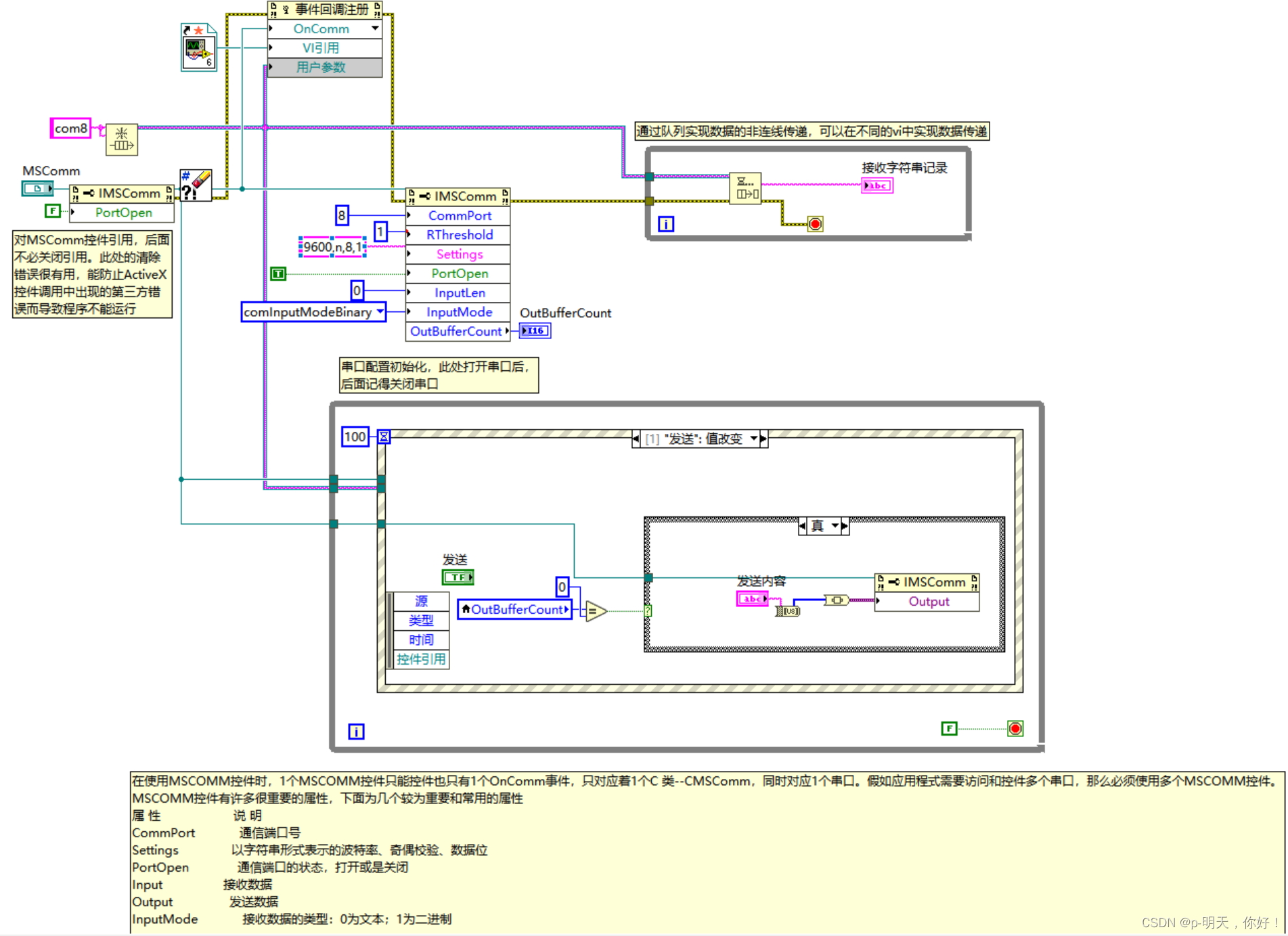
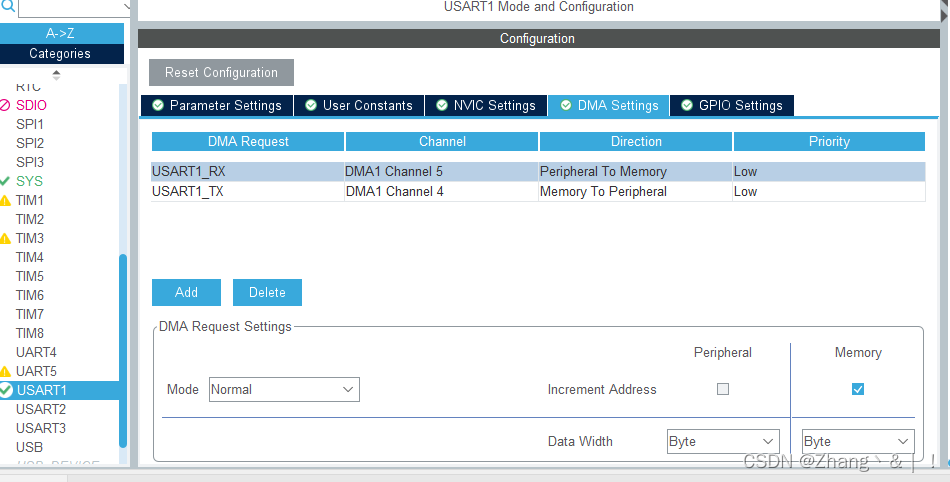
Labview串口通信MSComm实现串口收发
文章目录 前言一、什么是 MSComm二、MSComm 控件下载三、MSComm 控件的注册四、使用 MSComm 控件1、前面板放置控件2、MSComm 的常用属性3、MSComm 控件的事件 五、实现串口收发1、搭建虚拟串口2、发送测试3、接收测试4、后面板核心程序框图 六、程序自取 前言 本文介绍使用 A…...
字节跳动 EB 级 Iceberg 数据湖的机器学习应用与优化
深度学习的模型规模越来越庞大,其训练数据量级也成倍增长,这对海量训练数据的存储方案也提出了更高的要求:怎样更高性能地读取训练样本、不使数据读取成为模型训练的瓶颈,怎样更高效地支持特征工程、更便捷地增删和回填特征。本文…...

CentOS 安装Mysql8
1.检查是否已经安装mysql,停止mysql服务,删除mysql ps -ef | grep -i mysql systemctl stop mysqld rpm -e mysql 2.配置仓库 更新秘钥 rpm --import https://repo.mysql.com/RPM-GPG-KEY-mysql-2022 安装mysql8的yum源 rpm -Uvh https://dev.mysql.…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
