经典面试题(力扣,接雨水)
接雨水
- 方法一
- 思路
- 测试代码
- 复杂度
- 测试结果
- 方法二
- 思路
- 测试代码
- 复杂度
- 测试结果
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例1:
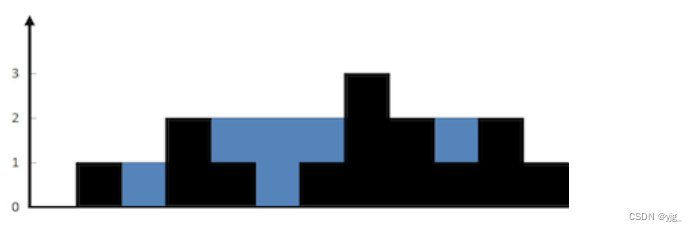
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,
在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105
方法一
思路
我们需要维护一个到当前的前缀最大数组(当前元素的前缀最大的数字),和一个到当前的后缀最大数组(当前元素的后缀最大的数字)。
当我们遍历到当前元素的时候,选出前缀和后缀二者中小的那个减去高度即可,得到当前元素的接住的雨水量.

比如相对于这个 height = [0,1,0,2,1,0,1,3,2,1,2,1]高度图,
前缀最大数组是 :pre_max:[0,1,1,2,2,2,2,3,3,3,3,3];
后缀最大数组是: sub_max:[3,3,3,3,3,3,3,3,2,2,2,1];
把遍历到的每一个元素当成一个宽度为1的水桶,他的高就是与其索引一样的前缀最大数组和后缀最大数组中的最小的一个。
测试代码
class Solution{public int trap(int[] height) {int ans=0;int n=height.length;//数组前缀最大值int pre_max[]=new int[n];pre_max[0]=height[0];//后缀最大值数组int sub_max[]=new int[n];sub_max[n-1]=height[n-1];for (int i = 1; i <n; i++) {pre_max[i]=Math.max(height[i],pre_max[i-1]);}for (int i = n-2; i >=0; i--) {sub_max[i]=Math.max(height[i],sub_max[i+1]);}for (int i = 0; i <n; i++) {ans+=Math.min(pre_max[i],sub_max[i])-height[i];}return ans;}
}
复杂度
时间复杂度是:O(n),n,是数组的长度,因为只有三个单层for循环。
空间复杂度是:O(n),创建了两个为长度为n的数组。
测试结果

方法二
思路
我们可以定义两个变量,来维护相对于当前元素的前缀最大值,和后缀最大值。
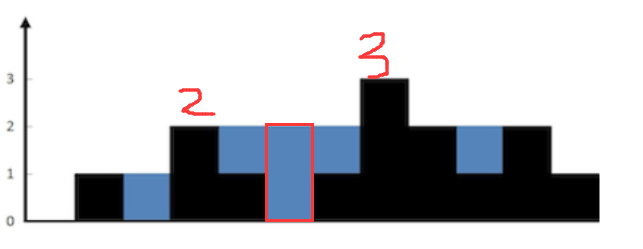
比如这个时候,当我们遍历到红色的框框时候,前缀最大值是2,后缀最大值是3,那么它形成的宽为1木桶,水桶高选择的是前缀,和,后缀小的那个(因为水桶的高度只能选择较小的不,选择大的会溢出去),然后减去高就可以得到当前元素的接雨水的量。
测试代码
class Solution {public int trap(int[] height) {//答案和int ans=0;//前缀最大值int pre_max=0;//后缀最大值int sub_max=0;int i=0,j=height.length-1;while (i<j){//更新前缀最大值pre_max=Math.max(pre_max,height[i]);//更新后缀最大值sub_max=Math.max(sub_max,height[j]);if (pre_max<sub_max){//前缀较小,更新答案ans+=pre_max-height[i];i++;}else {//后缀较小或者等于情况,更新答案ans+=sub_max-height[j];j--;}}return ans;}
}
复杂度
时间复杂度是:O(n)
空间复杂度是:O(1)
测试结果
相关文章:

经典面试题(力扣,接雨水)
接雨水 方法一思路测试代码复杂度测试结果 方法二思路测试代码复杂度测试结果 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1]…...

2023年深圳杯数学建模C题无人机协同避障航迹规划
2023年深圳杯数学建模 C题 无人机协同避障航迹规划 原题再现: 平面上A、B两个无人机站分别位于半径为500 m的障碍圆两边直径的延长线上,A站距离圆心1 km,B站距离圆心3.5 km。两架无人机分别从A、B两站同时出发,以恒定速率10 m/s…...
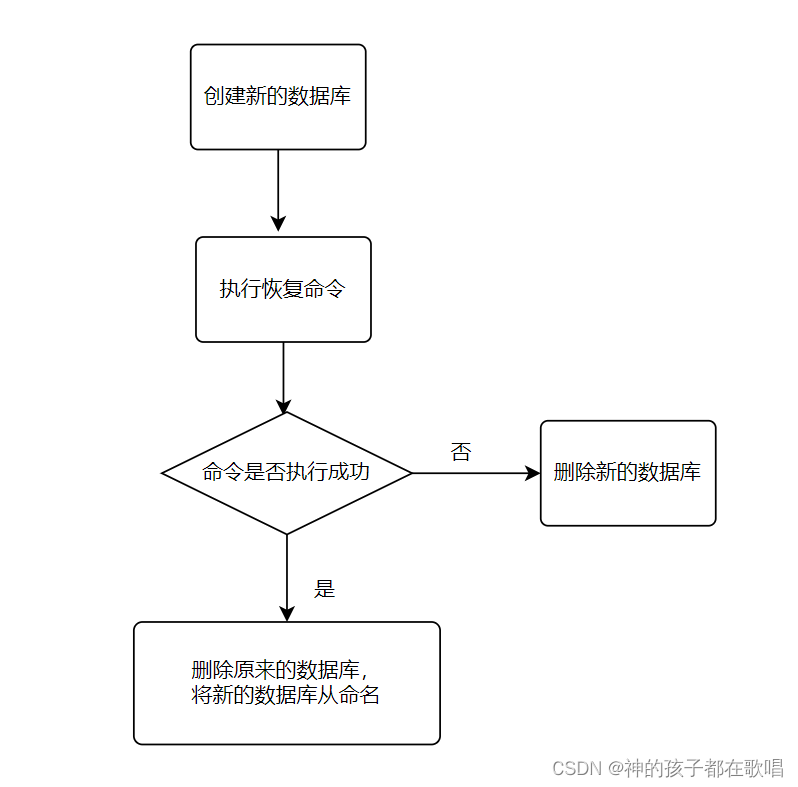
PostgreSQL--实现数据库备份恢复详细教学
前言 这是我在这个网站整理的笔记,关注我,接下来还会持续更新。 作者:RodmaChen PostgreSQL--实现数据库备份恢复详细教学 一. 数据库备份二. 数据库恢复三. 存留问题 数据库备份恢复功能是每个产品所需的,以下是简单的脚本案例&a…...

JDK工具之jstack说明
JDK工具之jstack说明 前言什么是jstack?如何使用jstack?获取Java进程的PID分析jstack输出 常用的jstack命令选项jstack的应用场景结论 前言 作为Java开发人员,在开发和维护复杂的Java应用程序时,我们经常会遇到各种各样的问题&am…...

34 | 牛顿迭代法
文章目录 牛顿迭代法一、原理二、Python实现三、练习题四、总结牛顿迭代法 一、原理 牛顿迭代法(Newton’s Method)是一种用于寻找方程的实根的数值方法。其基本思想是通过一系列逼近来求解方程的根。对于方程 f ( x ) = 0 f(x) = 0 f(x...

ChatGPT如何帮助学生学习
一些教育工作者担心学生可能使用ChatGPT作弊。因为这个AI工具能写报告和计算机代码,画出复杂图表……甚至已经有许多学校把ChatGPT屏蔽。 研究发现,学生作弊的主要原因是想考得好。是否作弊与作业和考试的打分方式有关,所以这与技术的便…...

easyexcel导出excel-50行代码搞定大量数据导出
文章目录 一、写在前面二、使用步骤定义导出的数据实体导出 一、写在前面 场景: 当数据量导出过大时如果一次从数据库取出所有数据会导致内存飙升导致系统奔溃,所以我们采取循环读取和循环写入。 准备: mave导入:easyexcel:3.0.5 二、使用…...
OpenAI宣布安卓版ChatGPT正式上线;一站式 LLM底层技术原理入门指南
🦉 AI新闻 🚀 OpenAI宣布安卓版ChatGPT正式上线 摘要:OpenAI今日宣布,安卓版ChatGPT已正式上线,目前美国、印度、孟加拉国和巴西四国的安卓用户已可在谷歌Play商店下载,并计划在下周拓展到更多地区。Chat…...
)
Rust vs Go:常用语法对比(二)
21. Swap values 交换变量a和b的值 a, b b, a package mainimport "fmt"func main() { a : 3 b : 10 a, b b, a fmt.Println(a) fmt.Println(b)} 103 fn main() { let a 3; let b 10; let (a, b) (b, a); println!("a: {a}, b: {b}", aa,…...

对于Vue3的一些思考
看完 Vue Hooks: 让Vue开发更简单与高效 - 掘金 一些小心得 vue3: 组合式API(是利用架构,强制达到拆分目的) 达到解耦的目的。对于vue3来说 每个模块的每个逻辑都是 一个一个独立的方法。通过 方法方法整体业务 代码风格&#…...

Bean的生命周期 - spring
前言 本篇介绍了Bean的生命周期,认识PostConstruct注释,PreDestroy注释,如有错误,请在评论区指正,让我们一起交流,共同进步! 文章目录 前言1. spring生命周期2. Bean的生命周期3. 为什么先设置…...

入门Linux基本指令(2)
这篇文章主要提供一些对文件操作的Linux基本指令,希望对大家有所帮助,三连支持! 目录 cp指令(复制) mv指令(剪切) nano指令 cat指令(打印文件内容) > 输出重定向 >> 追加重定向 < 输入重定向 more指令 less指令(推荐) …...
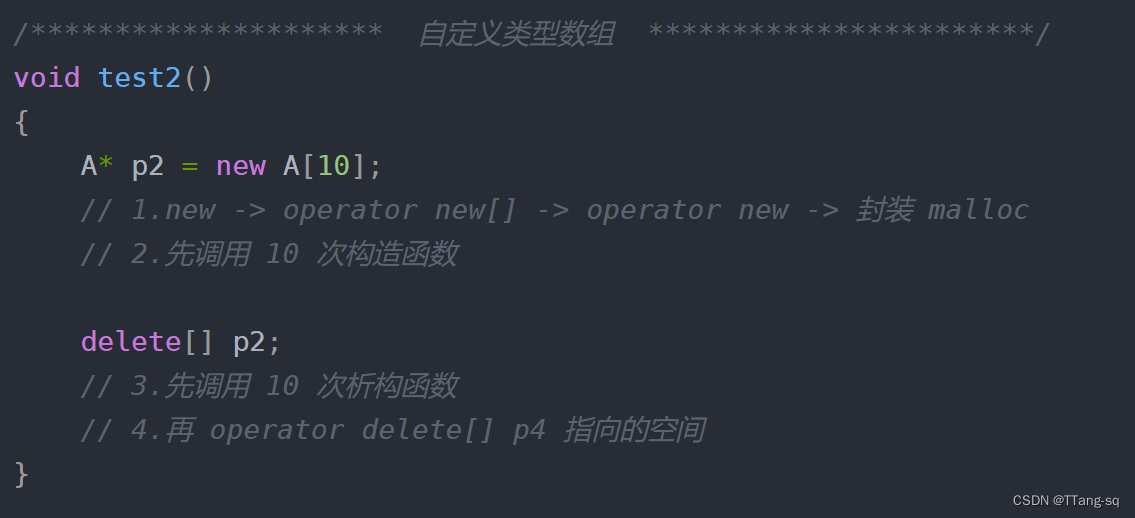
【C++】【自用】选择题 刷题总结
文章目录 【类和对象】1. 构造、拷贝构造的调用2. 静态成员变量3. 初始化列表4. 成员函数:运算符重载5. 友元函数、友元类55. 特殊类设计 【细节题】1. 构造 析构 new \ deletet、new[] \ delete[] 【类和对象】 1. 构造、拷贝构造的调用 #include using namespace…...
)
SkyWalking链路追踪-Collector(收集器)
Collector(收集器) SkyWalking的Collector(收集器)是SkyWalking链路追踪的核心组件之一。它负责接收来自各个Agent的追踪数据,并将其存储到数据存储器(如数据库)中。具体来说,Colle…...

typescript自动编译文件实时更新
npm install -g typescripttsc --init 生成tsconfig.json配置文件 tsc -w 在监听模式下运行,当文件发生改变的时候自动编译...
qt6.5 download for kali/ubuntu ,windows (以及配置选项选择)
download and sign in qt官网 sign in onlion Install 1 2 3 4 5...

【JS 原型链】
JavaScript 原型链是一个重要的概念,它是 JavaScript 语言实现面向对象编程的核心。在 JavaScript 中,每个对象都有一个与之关联的原型,并且该对象继承了原型中的属性和方法。这些原型组成了一个原型链,可以通过该链追溯到顶层的 …...
概述)
harmonyOS 开发之UI开发(ArkTS声明式开发范式)概述
UI开发(ArkTS声明式开发范式)概述 基于ArkTS的声明式开发范式的方舟开发框架是一套开发极简、高性能、支持跨设备的UI开发框架,提供了构建OpenHarmony应用UI所必需的能力,主要包括: ArkTS ArkTS是UI开发语言ÿ…...
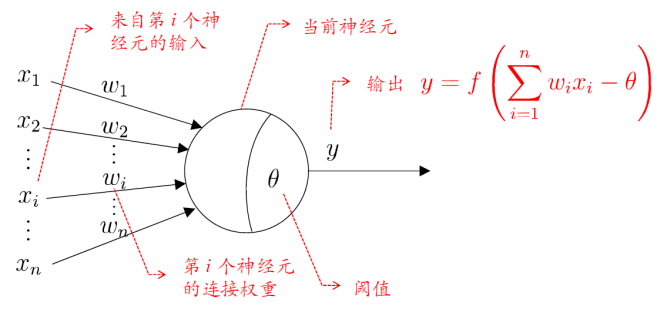
【人工智能】神经网络、M-P_神经元模型、激活函数、神经网络结构、学习网络参数、代价定义、总代价
M-P_神经元模型、激活函数、神经网络结构、学习网络参数、代价定义 文章目录 M-P_神经元模型、激活函数、神经网络结构、学习网络参数、代价定义M-P 神经元模型激活函数(Activation function)神经网络结构举例训练神经网络学习网络参数代价定义均方误差交叉熵(Cross Entropy)…...
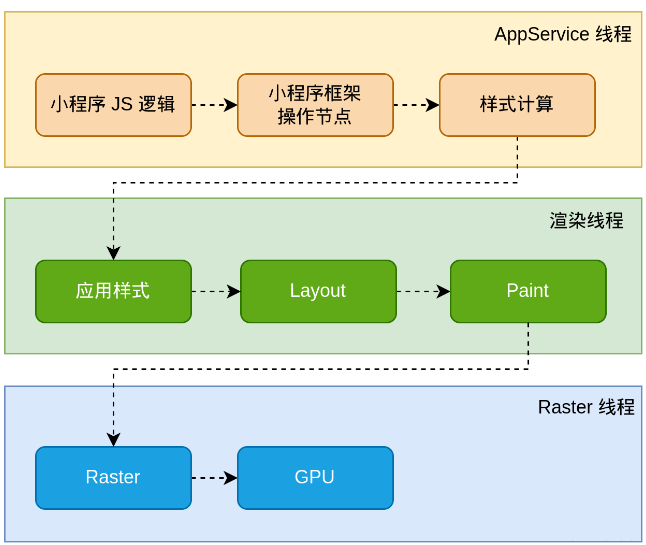
小程序新渲染引擎 Skyline 发布正式版
为了进一步提升小程序的渲染性能和体验,我们推出了一套新渲染引擎 Skyline,现在,跟随着基础库 3.0.0 发布 Skyline 正式版。 我们知道,小程序一直用 WebView 来渲染界面,因其有不错的兼容性和丰富的特性,且…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
