决策树概述
文章目录
- 决策树介绍
- 1.介绍
- **决策树API:**
- 构建决策树的三个步骤
- 决策树的优缺点
- 通过sklearn实现决策树分类并进一步认识决策树
- 2. ID3 决策树
- 1. 信息熵
- 2. 信息增益
- **定义:**
- **根据信息增益选择特征方法是:**
- **算法:**
- 3. ID3算法步骤
- 4. 例子:
- 3. C4.5 决策树
- 1. 信息增益率计算公式
- 2. 信息增益率计算举例
- 3. ID3和C4.5对比
- 4.CART 分类决策树
- 1. Cart树简介
- 2. 基尼指数计算公式
- 3. 基尼指数计算举例
- 3.1 是否有房
- 3.2 婚姻状况
- 3.3 年收入
- 4. Cart分类树原理
- 2.3 使用CART算法构建决策树
- 5. Cart回归决策树
- 1. 回归决策树构建原理
- 2.**CART 回归树构建过程如下:**
- 3.**例子:**
- 6. 剪枝
- 1 什么是剪枝?
- 2 为什么要进行树的剪枝?
- 3. 常见减枝方法汇总
- 方法介绍
- 优缺点对比
- 案例-泰坦尼克号生存预测
- 1. 案例背景
- 2. 案例实现
- 2.1 导入数据
- 2.2 数据的分析和预处理
- 2.3 数据集划分
- 2.4 使用决策树模型进行预测
- 2.5 模型评估与树可视化
- 2.6 总结
决策树介绍
1.介绍
决策树算法是一种监督学习算法,英文是Decision tree。决策树思想类似于if-else这样的逻辑判断,这其中的if表示的是条件,if之后的then就是一种选择或决策。程序设计中的条件分支结构就是if-then结构,最早的决策树就是利用这类结构分割数据的一种分类学习方法。
- 决策树是一种树形结构
- 树中每个内部节点表示一个特征上的判断,
- 每个分支代表一个判断结果的输出
- 最后每个叶节点代表一种分类结果
- 是非参数学习算法
- 可以解决分类(多分类)问题
- 可以解决回归问题:落在叶子节点的数据的平均值作为回归的结果
决策树API:
- from sklearn.tree import DecisionTreeClassifier
- from sklearn.tree import plot_tree
构建决策树的三个步骤
-
特征选择:选取有较强分类能力的特征
问题: 如何判断特征的重要性?-
- 信息增益(ID3)
-
- 信息增益率(C4.5)
-
- 基尼指数(CART分类树)
-
- 平方损失(CART回归树)
-
-
决策树生成:典型的算法有ID3和C4.5,它们生成决策树过程相似,ID3是采用信息增益作为特征选择度量,而C4.5采用信息增益比率 , CART决策树则使用基尼指数
-
决策树剪枝:剪枝原因是决策树生成算法生成的树对训练数据的预测很准确,但是对于未知数据分类很差,这就产生了过拟合的现象。
决策树的优缺点
- 优点:可读性好,具有描述性,有助于人工分析;效率高,决策树只需要一次性构建反复使用,每一次预测的最大计算次数不超过决策树的深度
- 缺点:容易过拟合;不稳定,当数据发生微小变化时,模型差别可能会很大
通过sklearn实现决策树分类并进一步认识决策树
基于鸢尾花数据绘制图像
import numpy as np
import matplotlib.pyplot as pltfrom sklearn import datasetsiris = datasets.load_iris()
X = iris.data[:,2:]
y = iris.target
# 画出数据分布的散点图
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])plt.show()

训练决策树模型
from sklearn.tree import DecisionTreeClassifiertree = DecisionTreeClassifier(max_depth=2,criterion="entropy")
tree.fit(X,y)
依据模型绘制决策树的决策边界
#找到模型的决策边界,并绘制图像
def plot_decision_boundary(model,axis):x0,x1 = np.meshgrid(np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1))X_new = np.c_[x0.ravel(),x1.ravel()]y_predict = model.predict(X_new)zz = y_predict.reshape(x0.shape)from matplotlib.colors import ListedColormapcustom_map = ListedColormap(["#EF9A9A","#FFF59D","#90CAF9"])plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_map)plot_decision_boundary(tree,axis=[0.5,7.5,0,3])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.show()

树模型可视化
from sklearn.tree import plot_tree
import matplotlib.pyplot as pltplot_tree(tree,filled=True)
plt.show()

从上面的可视化图形中看出
- X[1] <=0.8 作为第一次分割的依据,满足条件的所有样本均为统一类别
- X[1]>0.8的,依据 X[1]<=0.75 为划分依据
- 由于设置了树的最大深度为2,第二层的两个叶子节点没有完全区分开,绿色的里面有5个应该是紫色的类型,紫色的里面有1个绿色类型的
2. ID3 决策树
ID3 树是基于信息增益构建的决策树,采用划分后样本集的不确定性作为衡量划分样本子集的好坏程度,用信息增益度量不确定性----信息增益越大,不确定性越小
1. 信息熵
-
定义----熵在信息论中代表随机变量不确定度的度量。
- 熵越大,该变量包含的信息量就大,数据的不确定性度越高
- 熵越小,数据的不确定性越低
-
公式
H = − ∑ i = 1 k p i log ( p i ) \large H = -\sum_{i=1}^{k}p_i\log(p_i) H=−i=1∑kpilog(pi)
例子1:假如有三个类别,分别占比为:{1/3,1/3,1/3},信息熵计算结果为:
H = − 1 3 log ( 1 3 ) − 1 3 log ( 1 3 ) − 1 3 log ( 1 3 ) = 1.0986 H=-\frac{1}{3}\log(\frac{1}{3})-\frac{1}{3}\log(\frac{1}{3})-\frac{1}{3}\log(\frac{1}{3})=1.0986 H=−31log(31)−31log(31)−31log(31)=1.0986
例子2:假如有三个类别,分别占比为:{1/10,2/10,7/10},信息熵计算结果为:
H = − 1 10 log ( 1 10 ) − 2 10 log ( 2 10 ) − 7 10 log ( 7 10 ) = 0.8018 H=-\frac{1}{10}\log(\frac{1}{10})-\frac{2}{10}\log(\frac{2}{10})-\frac{7}{10}\log(\frac{7}{10})=0.8018 H=−101log(101)−102log(102)−107log(107)=0.8018
熵越大,表示整个系统不确定性越大,越随机,反之确定性越强。
-
公式的转换 ------ 当数据类别只有两类的情况下,公式可以做如下转换
H = − ∑ i = 1 k p i log ( p i ) H = − x log ( x ) − ( 1 − x ) log ( 1 − x ) \begin{align}\large H &= -\sum_{i=1}^{k}p_i\log(p_i) \tag 1 \\ \large H &= -x\log(x)-(1-x)\log(1-x) \tag2 \\ \end{align} HH=−i=1∑kpilog(pi)=−xlog(x)−(1−x)log(1−x)(1)(2) -
代码角度理解信息熵的概念
import numpy as np
import matplotlib.pyplot as pltdef entropy(p):return -p*np.log(p)-(1-p)*np.log(1-p)x = np.linspace(0.01,0.99,200)
plt.plot(x,entropy(x))
plt.show()

观察上图可以得出,当我们的系统每一个类别是等概率的时候,系统的信息熵最高,当系统偏向于某一列,相当于系统有了一定程度的确定性,直到系统整体百分之百的都到某一类中,此时信息熵就达到了最低值,即为0。上述结论也可以拓展到多类别的情况。
2. 信息增益
定义:
特征 A A A对训练数据集D的信息增益 g ( D , A ) g(D,A) g(D,A),定义为集合 D D D的经验熵 H ( D ) H(D) H(D)与特征A给定条件下D的经验熵 H ( D ∣ A ) H(D|A) H(D∣A)之差。即
g ( D , A ) = H ( D ) − H ( D ∣ A ) \large g(D,A)=H(D)-H(D|A) g(D,A)=H(D)−H(D∣A)
根据信息增益选择特征方法是:
- 对训练数据集D,计算其每个特征的信息增益,
- 比较信息增益的大小,并选择信息增益最大的特征进行划分。表示由于特征 A A A而使得对数据D的分类不确定性减少的程度。
算法:
设训练数据集为D, ∣ D ∣ \mid D\mid ∣D∣表示其样本个数。
设有 K K K个类 C k C_k Ck, k = 1 , 2 , ⋯ , K k=1,2,\cdots,K k=1,2,⋯,K, ∣ C k ∣ \mid C_k\mid ∣Ck∣为属于类 C k C_k Ck的样本个数, ∑ k = 1 K = ∣ D ∣ \sum\limits_{k=1}^{K}=\mid{D}\mid k=1∑K=∣D∣。
设特征A有 n n n个不同取值 { a 1 , a 2 , ⋯ , a n } \{a_1, a_2, \cdots,a_n\} {a1,a2,⋯,a
相关文章:

决策树概述
文章目录 决策树介绍1.介绍**决策树API:**构建决策树的三个步骤决策树的优缺点通过sklearn实现决策树分类并进一步认识决策树2. ID3 决策树1. 信息熵2. 信息增益**定义:****根据信息增益选择特征方法是:****算法:**3. ID3算法步骤4. 例子:3. C4.5 决策树1. 信息增益率计算…...
青枫壁纸小程序V1.4.0(后端SpringBoot)
引言 那么距离上次的更新已经过去了5个多月,期间因为忙着毕业设计的原因,更新的速度变缓了许多。所以,这次的更新无论是界面UI、用户功能、后台功能都有了非常大的区别。希望这次更新可以给用户带来更加好的使用体验 因为热爱,更…...
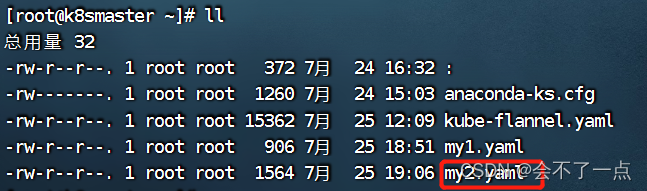
Error: unknown flag: --export 【k8s,kubernets报错】
报错情况如下: [rootk8smaster ~]# kubectl get deploy nginx -oyaml --export > my2.yaml Error: unknown flag: --export See kubectl get --help for usage.原因: --export在所使用的版本中已被移除 解决:去除--export即可,…...
进入linux系统中修改网段-ip
第一步 :开启虚拟机 cd 到 /etc/sysconfig/network-scripts 目录下,输入命令给ls,展示这个目录下文件和文件夹 第二步:进入到以ifcfg开头的文件 # ifcfg开头的文件,如果有多个网卡,有多个ifcfg-ensxx文件 命令…...
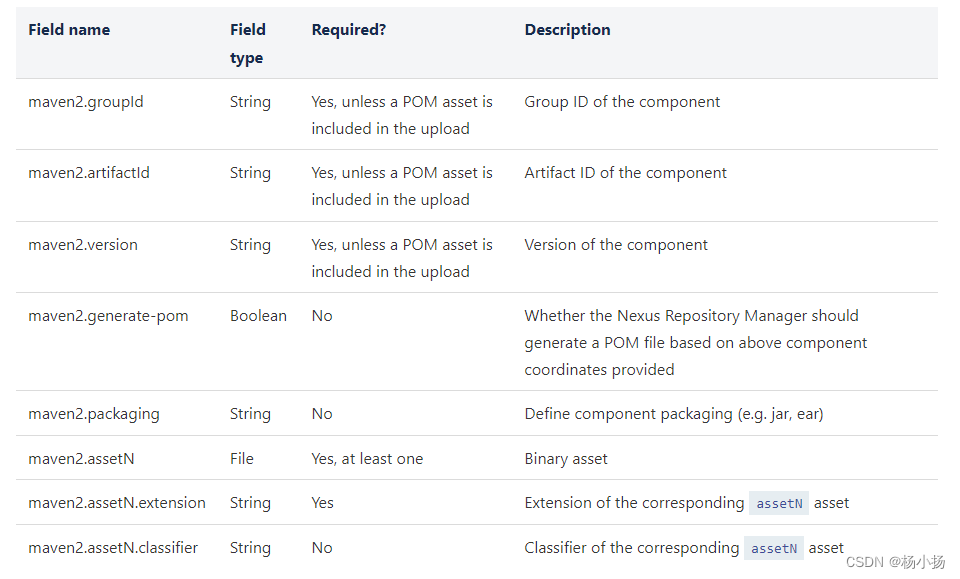
通过REST API接口上传Nexus仓库
一、Nexus API文档 API文档链接:Components API 二、上传API接口说明 在Nexus中可以直接调试api接口,url参考:http://localhost:8081/#admin/system/api 三、上传请求案例 $ curl -X POST "http://localhost:8081/service/rest/v1/c…...

Docker镜像端口映射简介及配置指南
目录 引言:什么是端口映射?配置端口映射的步骤:1. 创建Docker镜像:2. 选择要映射的端口:3. 运行容器并进行端口映射:4. 验证端口映射: 示例:结论: 引言: Doc…...
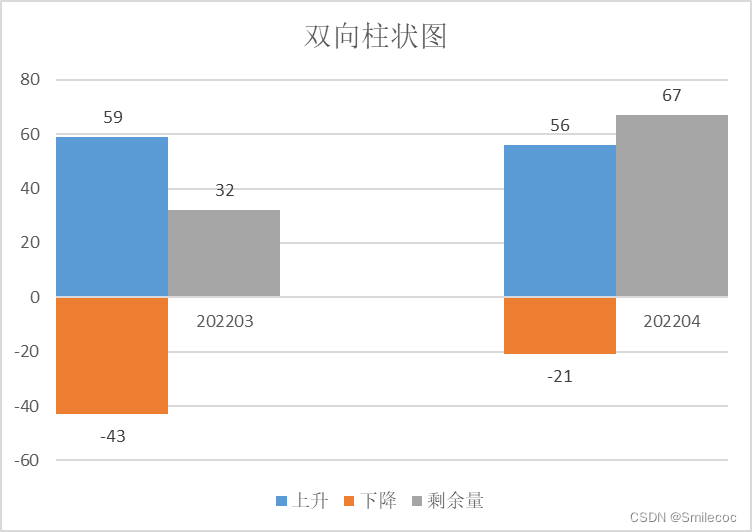
Excel双向柱状图的绘制
Excel双向柱状图在绘制增减比较的时候经常用到,叫法繁多,双向柱状图、上下柱状图、增减柱状图都有。 这里主要介绍一下Excel的基础绘制方法和复杂一点的双向柱状图的绘制 基础双向柱状图的绘制 首先升降的数据如下: 月份上升下降20220359-…...
Linux6.17 Docker 安全及日志管理
文章目录 计算机系统5G云计算第四章 LINUX Docker 安全及日志管理一、Docker 容器与虚拟机的区别1.隔离与共享2.性能与损耗 二、Docker 存在的安全问题1.Docker 自身漏洞2.Docker 源码问题 三、Docker 架构缺陷与安全机制1.容器之间的局域网攻击2.DDoS 攻击耗尽资源3.有漏洞的系…...

学好Elasticsearch系列-索引的CRUD
本文已收录至Github,推荐阅读 👉 Java随想录 文章目录 创建索引删除索引查询数据添加 & 更新数据cat命令公共参数 常用命令aliases 显示别名allocation 显示每个节点的分片数和磁盘使用情况count 显示整个集群或者索引的文档个数fielddata 显示每个节…...

Python - OpenCV机器视觉库的简单使用经验
OpenCV是一个开源的计算机视觉库,它支持多种编程语言,包括Python。下面是Python 3中OpenCV的详细解析: 安装OpenCV 在Python 3中安装OpenCV,可以使用pip命令来安装。例如,在终端中输入以下命令: pip ins…...
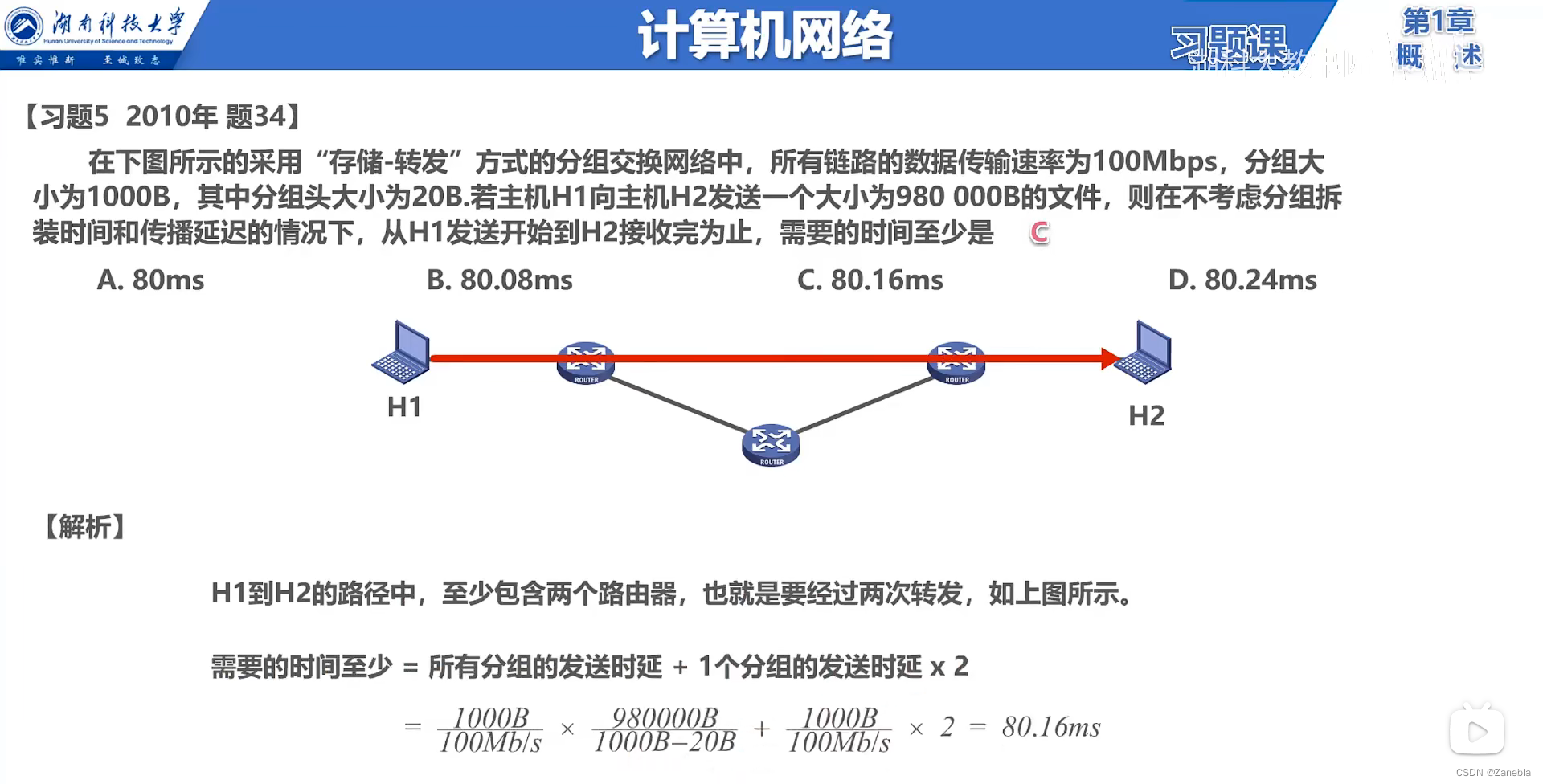
【计算机网络 01】说在前面 信息服务 因特网 ISP RFC技术文档 边缘与核心 交换方式 定义与分类 网络性能指标 计算机网络体系结构 章节小结
第一章--概述 说在前面1.1 计算机网络 信息时代作用1.2 因特网概述1.3 三种交换方式1.4 计算机网络 定义与分类1.5 计算机网络的性能指标1.6 计算机网络体系结构1 常见的计算机网络体系结构2 计算机网络体系结构分层的必要性3 计算机网络体系结构分层思想举例4 计算机网络体系结…...

POI信息点的diPointX、diPointY转化成经纬度
需求:接口返回某个地点的数据(diPointX、diPointY),前端需把该地点转化成经纬度形式在地图上进行Marker标记。 实现:(查找百度地图开发文档) 代码验证: console.log(new BMap.Merca…...
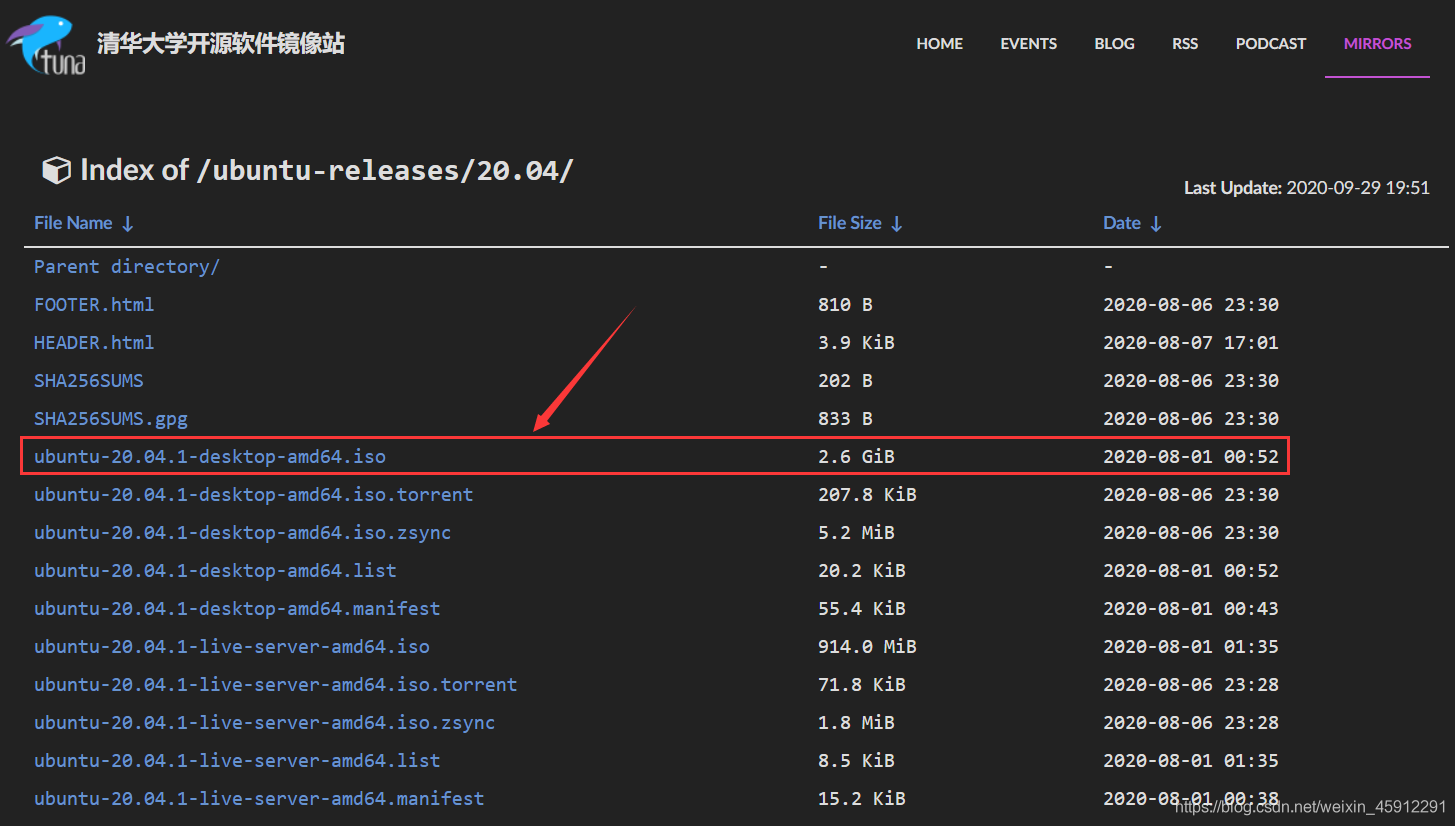
虚拟机(VMware)安装Linux(Ubuntu)安装教程
清华大学开源网站镜像站网址:清华大学开源软件镜像站 | Tsinghua Open Source Mirror 进入之后在搜索框中搜索“ubuntu” 直接点击箭头所指的蓝色字体“ubuntu-20.04.1-desktop-amd64.iso”即可下载...
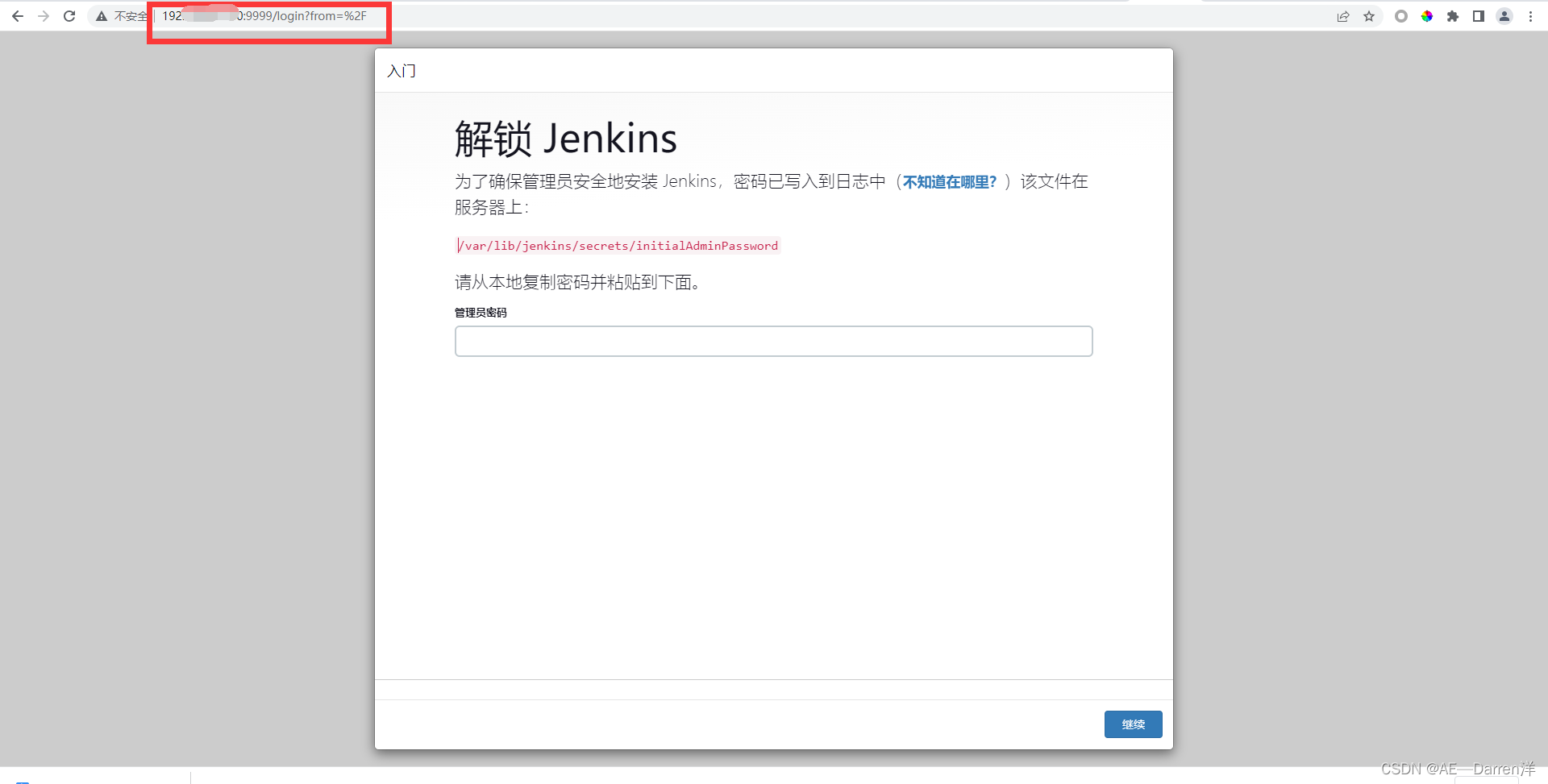
linux系统下(centos7.9)安装Jenkins全流程
一、卸载历史版本 # rpm卸载 rpm -e jenkins# 检查是否卸载成功 rpm -ql jenkins# 彻底删除残留文件 find / -iname jenkins | xargs -n 1000 rm -rf二、环境依赖安装 yum -y install epel-releaseyum -y install daemonize三、安装Jenkins Jenkins官网传送带: …...
Java版知识付费源码 Spring Cloud+Spring Boot+Mybatis+uniapp+前后端分离实现知识付费平台
提供职业教育、企业培训、知识付费系统搭建服务。系统功能包含:录播课、直播课、题库、营销、公司组织架构、员工入职培训等。 提供私有化部署,免费售后,专业技术指导,支持PC、APP、H5、小程序多终端同步,支持二次开发…...
[OnWork.Tools]系列 01-简介
说明 OnWork.Tools 是基于 Net6 的桌面程序。支持Windows7SP1及以上系统,主要是日常办公或者是开发工作过程中常用的工具集合。界面使用WPF Mvvm模式开发,目的是将开源项目中,好用的项目集成到一起,方便大家使用和学习。 功能 …...

神码ai火车头伪原创设置【php源码】
大家好,给大家分享一下python考什么内容,很多人还不知道这一点。下面详细解释一下。现在让我们来看看! 火车头采集ai伪原创插件截图: 1、Python 计算机二级都考什么 Python要到什么程度 考试内容 一、Python语言的基本语法元素…...
)
QEMU源码全解析15 —— QOM介绍(4)
接前一篇文章:QEMU源码全解析14 —— QOM介绍(3) 本文内容参考: 《趣谈Linux操作系统》 —— 刘超,极客时间 《QEMU/KVM》源码解析与应用 —— 李强,机械工业出版社 特此致谢! 上一回讲到pci…...

【QT】Day 2
1> 继续完善登录框,当登录成功时,关闭登录界面,跳转到新的界面中 second.h #ifndef SECOND_H #define SECOND_H#include <QWidget>namespace Ui { class second; }class second : public QWidget {Q_OBJECTpublic:explicit second…...

腾讯云 Cloud Studio 实战训练营活动招募中
点击链接了解详情...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
