CSS :nth-child
CSS :nth-child
:nth-child 伪类根据元素在同级元素中的位置来匹配元素.
- CSS :nth-child
- 语法
- 值是关键词 odd/even
- An+B
- 最新的 [of S] 语法
- 权重
- 浏览器兼容性
- 语法
很简单的例子, 来直觉上理解这个伪类的意思
<ul><li class="me">Apple</li><li>Banana</li><li class="me">Peach</li>
</ul>
<ul><li>Apple</li><li class="me">Banana</li><li class="me">Peach</li>
</ul>
.me:nth-child(1) { background-color: salmon; }

你也许会奇怪🤔, 为什么下边一组的 Banana 背景不是红色呢? 因为 .me:nth-child(1) 表示选中同级元素中的第一个元素并且该元素 class 包含 me✅, 注意不是选中第一个 class 包含 me 的元素. 所以, 如果同级元素中的第一个元素的 class 不包含 me, 也不会选中.
语法
在 :nth-child() 语法中, 统计的元素包含同级的任何类型元素.
:nth-child() 的完整语法如下, ? 前面的 [] 中内容表示可选, 稍后会介绍这种最新的部分. :nth-child() 只接受一个参数, 该参数描述匹配同级元素的模式, 元素索引从 1 开始, 注意不是 0.
:nth-child(<nth> [of S]?) { ... }
值是关键词 odd/even
odd: 表示在同级元素中奇数位置的元素: 1、3、5…even: 表示在同级元素中偶数位置的元素: 2、4、6…
比如, 在一个表格中我们希望相邻行的背景颜色不同, 这样方便阅读, 就可以这样写
tr:nth-child(even) { background-color: azure; }
<table border="1"><thead><tr><th>NAME</th><th>AGE</th> <th>COUNTRY</th></tr></thead><tbody><tr><td>Levi</td> <td>18</td> <td>China</td></tr><tr><td>June</td> <td>23</td> <td>USA</td> </tr><tr><td>JiaXin</td> <td>20</td> <td>China</td></tr><tr><td>Mike</td> <td>22</td> <td>UK</td></tr></tbody>
</table>

An+B
不论是 odd 还是 even, 他们都是更普遍表达的特殊情况的简便写法. 使用 An+B 这种记号你可以自由定制你的匹配规则
A: 整数步长n: 非负整数, 从0开始B: 整数偏移量
为什么我们说 odd/even 是 An+B 特殊取值时的简便写法呢? 因为
odd->:nth-child(2n+1)even->:nth-child(2n)
下面我们就看看 An+B 取不同值的特定用法吧
:nth-child(2): 表示第二个元素

.two:nth-child(2) { background-color: salmon; }
<ul class="flex-1"><li class="two">1</li><li class="two">2</li><li class="two">3</li>
</ul>
<ul class="flex-1"><li class="two">1</li><li class="two" hidden>2</li> <!-- !!! --><li class="two">3</li>
</ul>
从上图中可以看到, 左边的符合我们的预期, 第二个元素并且 class 是 two 的元素背景红了, 但是左边的好像不太行, 因为 display 为 none 的元素也被考虑进来了!!!
-
:nth-child(3n): 表示第3、6、9…个元素.

-
:nth-child(n+5): 表示第5、6、7、8、9…个元素. 也就是第五个和后面的元素.

-
:nth-child(-n+3): 表示第1(-2+3)、2(-1+3)、3(-0+3)个元素. 如果n的值继续增加, 就会选中第0、-1、-2…个元素, 负数位置的元素不存在并且元素是从 1 开始索引的.

-
:nth-child(4n+1): 表示第1、5、9…个元素

-
:nth-child(n): 表示每一个元素 -
:nth-child(1): 表示第 1 个元素, 是n为 1 更特殊的情况

.n:nth-child(n) {background-color: salmon;
}
.n:nth-child(1) {border-width: 3px;
}
:nth-child(n+3):nth-child(-n+5): 表示第3、4、5个元素. 用于选择一个具有上下限范围内的元素

最新的 [of S] 语法
目前 :nth-child() 只能选择特定位置的元素, 比如 .name:nth-child(-n+3) 只能选择元素中 class 包含 name 的并且是所有元素中的前三个元素. 但是, 如果我们想要选择前三个 class 包含 name 的元素呢? 那就是最新的 of S 语法
下面的例子
.class1 > .item:nth-child(-n+3 of .name) {background-color: salmon;
}
<ul class="class1"><li class="name item">1</li><li class="item">2</li><li class="item">3</li><li class="item">4</li><li class="item">5</li><li class="name item">6</li><li class="item">7</li><li class="item">8</li><li class="name item">9</li><li class="name item">10</li>
</ul>

📖一定要留意两者的不同哦.
你可能问新的语法有什么用呢, 当然有用啦, 比如我们在给表格添加间隔背景时, 如果出现一行元素被隐藏的情况, 会出现什么效果呢?
tr:nth-child(even) {background-color: azure;
}
<tbody><tr></tr><tr hidden></tr><tr></tr><tr></tr>
</tbody>

哇! 被隐藏的那一行也被考虑进入了, 按理说应该只有第二行(JiaXin)才有阴影的, 怎么办呢? 使用 of S. 我们不是要选择偶数行, 而是要选择所有 hidden 为 false 的偶数行.
tr:nth-child(even of :not([hidden])) {background-color: azure;
}

权重
:nth-child() 的权重是单个伪类的权重. 如果使用 of S 语法, 那么就是单个伪类的权重加上 S 中权重最高的权重值.
<div><div id="country1" class="country1">CHINA</div>
</div>
.country1:nth-child(1) {color: blue; /** WIN */
}
.country1 {color: red;
}

如果我们再加一个呢?
:nth-child(1 of #country1.country1) {color: green; /** WIN */
}

浏览器兼容性
根据 MDN, of S 的新语法需要比较新的浏览器支持

谢谢你看到这里😊
相关文章:

CSS :nth-child
CSS :nth-child :nth-child 伪类根据元素在同级元素中的位置来匹配元素. CSS :nth-child 语法 值是关键词 odd/evenAnB最新的 [of S] 语法权重 浏览器兼容性 很简单的例子, 来直觉上理解这个伪类的意思 <ul><li class"me">Apple</li><li>B…...
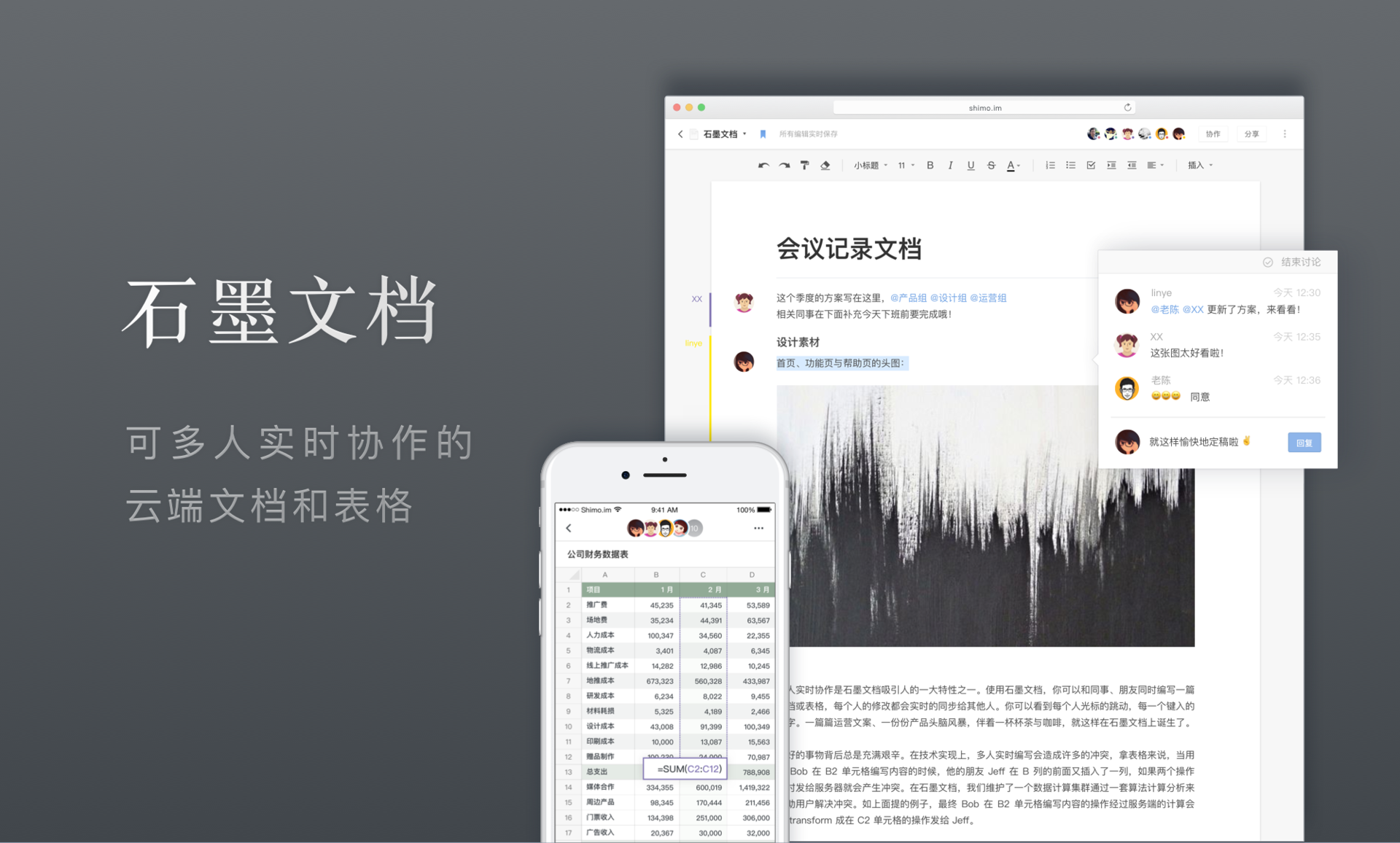
国内好用的企业级在线文档有哪些?
在当今数字化时代,企业级在线文档已经成为了现代办公环境中不可或缺的一部分。它不仅能够提高工作效率,还能够实现多人协同编辑,满足团队协作的需求。那么,在国内市场上,哪些企业级在线文档产品备受企业青睐呢…...

P1217 [USACO1.5] 回文质数 Prime Palindromes
题目描述 因为 151 151 151 既是一个质数又是一个回文数(从左到右和从右到左是看一样的),所以 151 151 151 是回文质数。 写一个程序来找出范围 [ a , b ] ( 5 ≤ a < b ≤ 100 , 000 , 000 ) [a,b] (5 \le a < b \le 100,000,000…...

【STM32MP1系列】DDR内存测试用例
DDRDDR内存测试 一、uboot下测试DDR内存二、Linux内核下测试DDR内存1、使用memtester测试DDR内存2、使用stressapptest测试DDR内存三、Buildroot中构建memtester软件包四、搭建stressapptest软件包五、注意事项一、uboot下测试DDR内存 输入bdinfo查看DDR起始地址以及大小: b…...
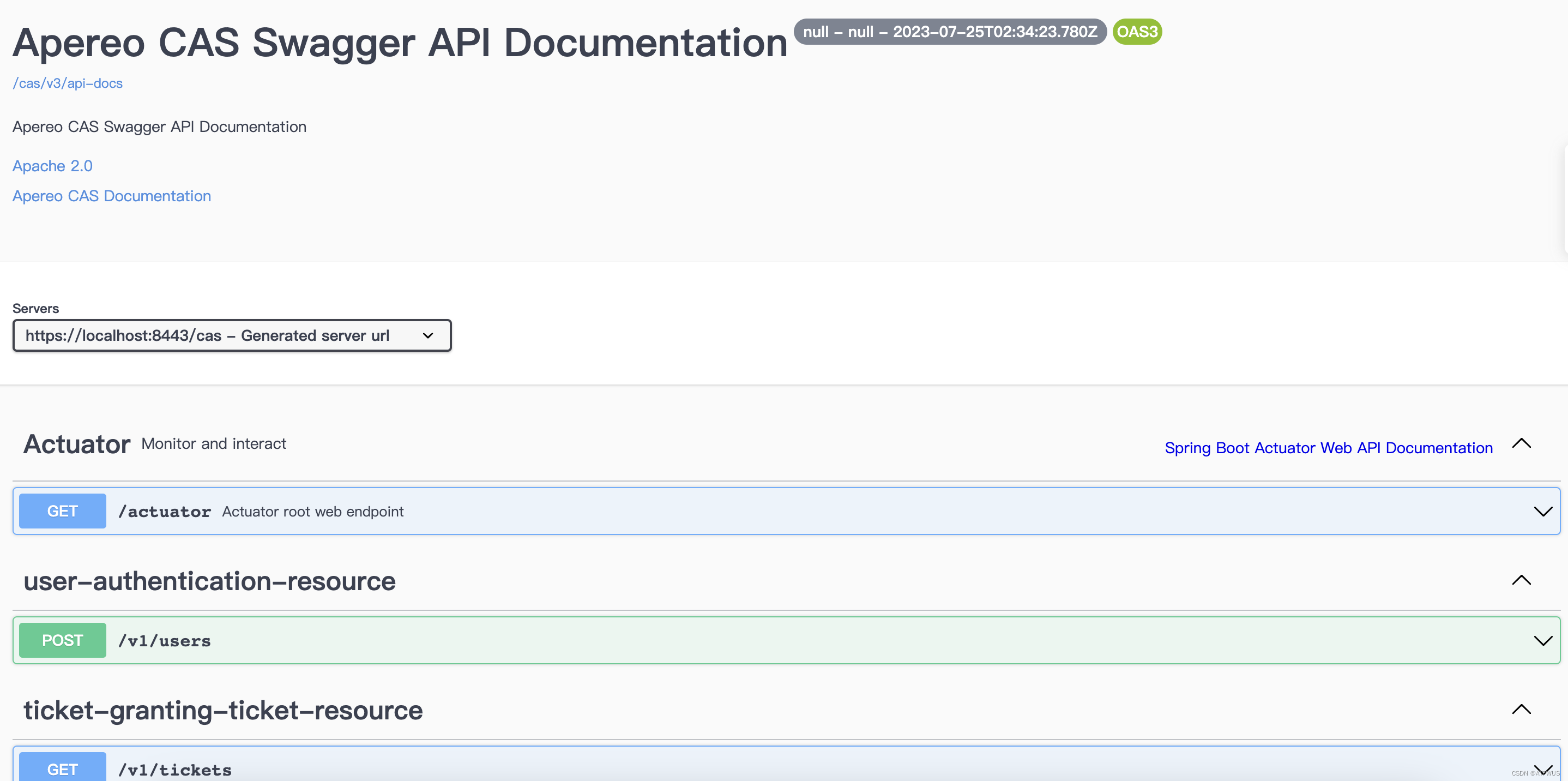
【CAS6.6源码解析】调试Rest API接口
CAS的web层默认是基于webflow实现的,ui和后端是耦合在一起的,做前后端分离调用和调试的时候不太方便。但是好在CAS已经添加了支持Rest API的support模块,添加相应模块即可。 文章目录 添加依赖并重新build效果 添加依赖并重新build 具体添加…...

C++设计模式之模板方法、策略模式、观察者模式
面向对象设计模式是”好的面向对象设计“,所谓”好的面向对象设计“指的是可以满足”应对变化,提高复用“的设计。 现代软件设计的特征是”需求的频繁变化“。设计模式的要点是”寻求变化点,然后在变化点处应用设计模式,从而更好地…...
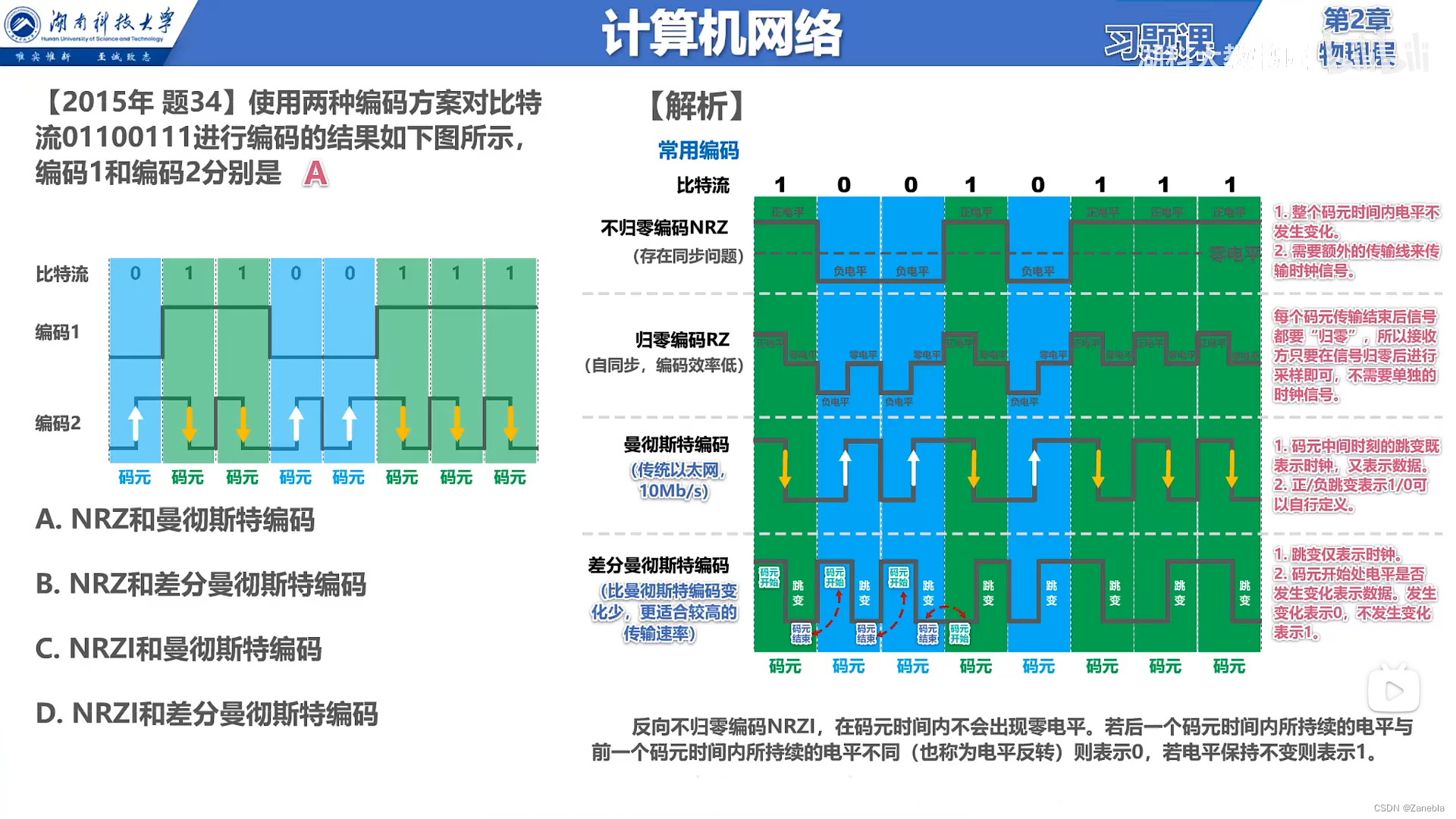
【计算机网络 02】物理层基本概念 传输媒体 传输方式 编码与调制 信道极限容量 章节小结
第二章 -- 物理层 2.1 物理层基本概念2.2 物理层下的传输媒体2.3 传输方式2.4 编码与调制2.5 信道极限容量2.6 章节小结 2.1 物理层基本概念 2.2 物理层下的传输媒体 传输媒体也称为传输介质或传输媒介,他就是数据传输系统中在发送器和接收器之间的物理通路 传输媒…...

无涯教程-jQuery - serialize( )方法函数
serialize()方法将一组输入元素序列化为数据字符串。 serialize( ) - 语法 $.serialize( ) serialize( ) - 示例 假设无涯教程在serialize.php文件中具有以下PHP内容- <?php if( $_REQUEST["name"] ) {$name$_REQUEST[name];echo "Welcome ". $na…...

一套不错的基于uniapp实现的投票类小程序/H5
最近作者心血来潮,想做一个热点话题投票,话题相关的资讯跟踪类的小程序,方便自己发布一些大家比较关心的话题。 基于以上需求,说干就干,首先需要定义一个需求: 1、支持热门话题投票、排行榜(日…...
Mac代码编辑器sublime text 4中文注册版下载
Sublime Text 4 for Mac简单实用功能强大,是程序员敲代码必备的代码编辑器,sublime text 4中文注册版支持多种编程语言,包括C、Java、Python、Ruby等,可以帮助程序员快速编写代码。Sublime Text的界面简洁、美观,支持多…...

django------模糊查询
1.常用模糊查询的方法 queryset中支持链式操作 bookBook.objects.all().order_by(-nid).first() 只要返回的是queryset对象就可以调用其他的方法,直到返回的是对象本身 大于、大于等于、小于、小于等于: # __gt 大于> # __gte 大于等于> # __lt 小于< …...

AVFoundation - 音视频组合编辑
文章目录 一、简要说明二、使用1、音频和视频合成2、视频的拼接一、简要说明 相关类 AVMutableCompositionAVMutableCompositionTrack二、使用 1、音频和视频合成 - (void)testCom1{AVMutableComposition *mutableComposition = [AVMutableComposition composition];AVMu...
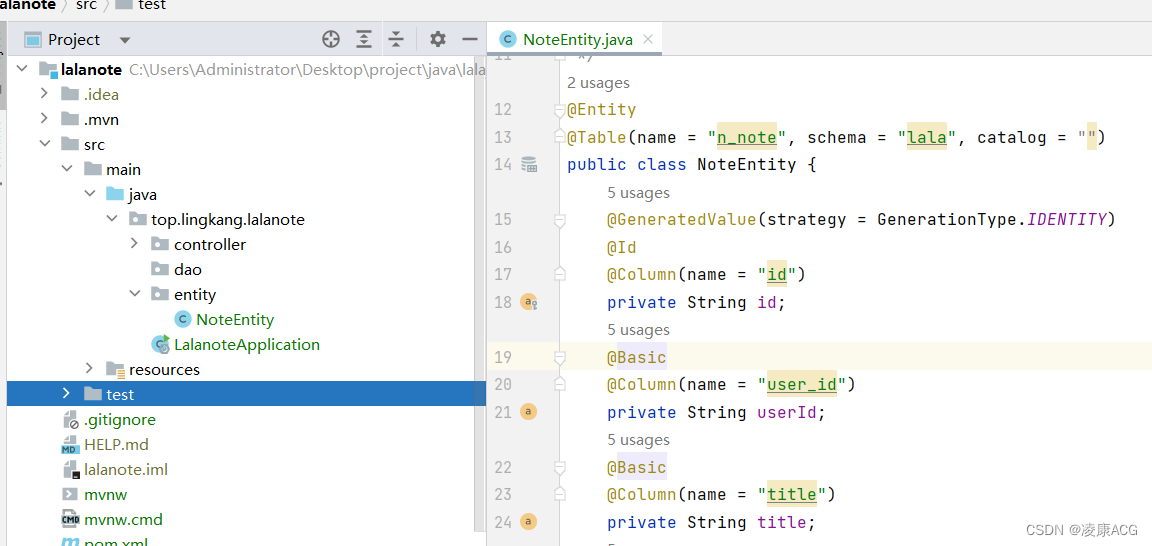
jpa生成实体类,jpa根据数据库表生成实体类
jpa生成实体类,jpa根据数据库表生成实体类jpa根据数据库表结构生成实体idea下SpringbootJPA从数据库自动生成实体类JPA用数据库表直接生成实体类Spring boot整合jpa(一),根据表生成实体IDEA下SpringData-JPA根据数据库表生成实体类idea怎么根据数据库表自动生成JPA实…...

嵌入式Linux系统组成
嵌入式Linux系统的组成 文章目录 嵌入式Linux系统的组成一、发行版Linux系统VS嵌入式Linux系统二、嵌入式Linux系统架构一、发行版Linux系统VS嵌入式Linux系统 1.产品 发行版Linux系统产品:服务器、消费平板、消费手提电脑 嵌入式Linux系统产品:扫地机器人,小米机顶盒特定场…...
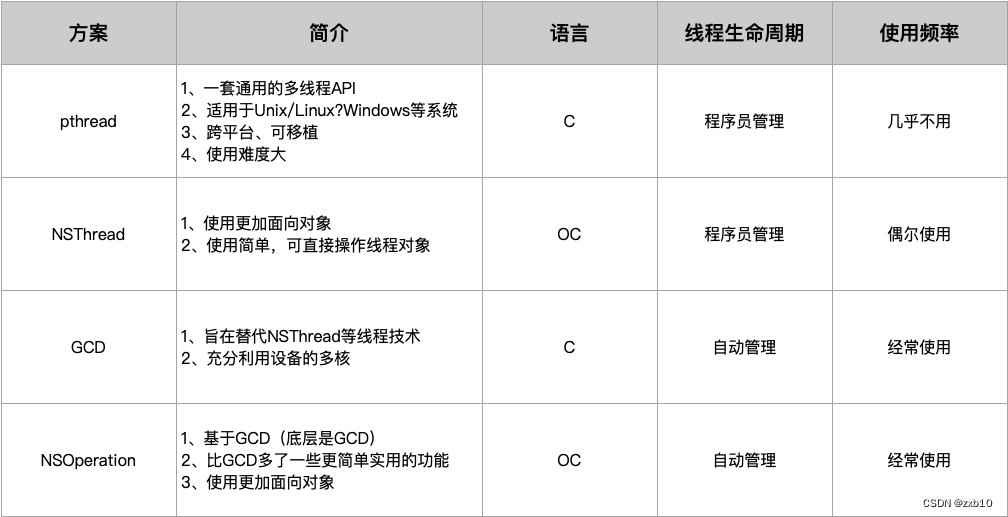
【iOS】—— RunLoop和多线程相关问题总结
RunLoop 1. 讲讲RunLoop,项目中有用到过吗? RunLoop 的基本作用:保持程序的持续运行,节省 CPU 的资源,提高程序的性能 ( 没有事情,就请休眠,不要功耗。有事情,就处理&a…...
)
在CSDN学Golang云原生(gitlab)
一,基于Docker安装gitlab runner 在Golang中,基于Docker安装GitLab Runner需要以下步骤: 首先,您需要安装Docker和Docker Compose。这可以通过访问官方网站来完成。接下来,您需要创建一个名为docker-compose.yml的文…...

cv2抛出异常 “install libgtk2.0-dev and pkg-config, then re-run cmake or configure”
背景: linux中使用cv2显示图片的时候,运行提示异常: 处理方式: 网友的推荐操作: 切换至root模式安装 apt-get install libgtk2.0-dev进入OpenCV下载目录,重新编译 cd /home/XXX/opencv mkdir release …...
C#..上位机软件的未来是什么?
C#是一种流行的编程语言,广泛应用于桌面应用程序和上位机软件开发。未来,C#上位机软件将继续不断发展和创新,以满足用户日益增长的需求。以下是我认为C#上位机软件未来可能会涉及的一些方向: 更加智能化:随着人工智能…...
CentOS 搭建 GitLab Git
本文目录 1. CentOS7 搭建 Gitlab1. 安装 sshd1. 安装 sshd 依赖2. 启动并设置开机自启3. 安装防火墙4. 开启防火墙5. 开放 ssh 以及 http 服务 2. 安装 postfix1. 安装 postfix2. 启动并设置开机自启3. 几个补充知识 3. 下载并安装 gitlab1. 在线下载安装包2. 安装 4. 修改 gi…...

【MTK平台】【wpa_supplicant】关于wpa_supplicant_8/src/p2p/p2p_go_neg.c文件的介绍
本文主要介绍external/wpa_supplicant_8/src/p2p/p2p_go_neg.c文件 这里主要介绍2个方法 1. p2p_connect_send接受来自 p2p.c 文件中调用p2p_connect方法发送的GON Request帧 2. p2p_process_go_neg_resp处理来自GON Response帧的处理流程 先看下p2p_connect_send方法 int p…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
