【图论】三种中心性 —— 特征向量、katz 和 PageRank
维基百科:在图论和网络分析中,中心性指标为图中相应网络位置的节点分配排名或数值。中心性这一概念最初起源于社交网络分析,因此很多衡量中心性的术语也反映了其社会学背景。
不同中心性指标对 “重要” 的衡量方式不同,因此适用于不同的情形。
一、特征向量中心性(eigenvector centrality)
特征向量这一概念最早应该是在 线性代数 这门课程中接触到的,而取名中的特征向量也与它最初的概念相关,我们先回顾下什么是 “特征值” 和 “特征向量”。
1.1 线性代数中的特征向量
定义:设 A 是 n 阶方阵,若存在向量使得
,则称 x 为 A 的特征向量,
为 A 的特征值(严格定义请参考权威文献)。
由定义可见,特征向量的本质是它与原矩阵相乘后,得到的矩阵与特征向量方向相同,仅存在缩放关系(即 倍的缩放),该缩放比例称为特征值。进一步延伸,原矩阵无论乘上多少特征向量,其方向都是确定的。回顾一道求特征值和特征向量的简单例题,可以更好回忆相关概念,求
的特征向量和特征值。
解得两个特征值 2 或 4,则应有
解得 ,因此可取特征值 2 的特征向量为
.
求特征值 4 的特征向量同理。
1.2 图论中的特征向量中心性
定义:图 G = (V, E),定义其邻接矩阵 A, 表示节点 v 和 t 不相连,
表示节点 v 和 t 相连,则节点 v 的中心性 x 的分数计算式为
.
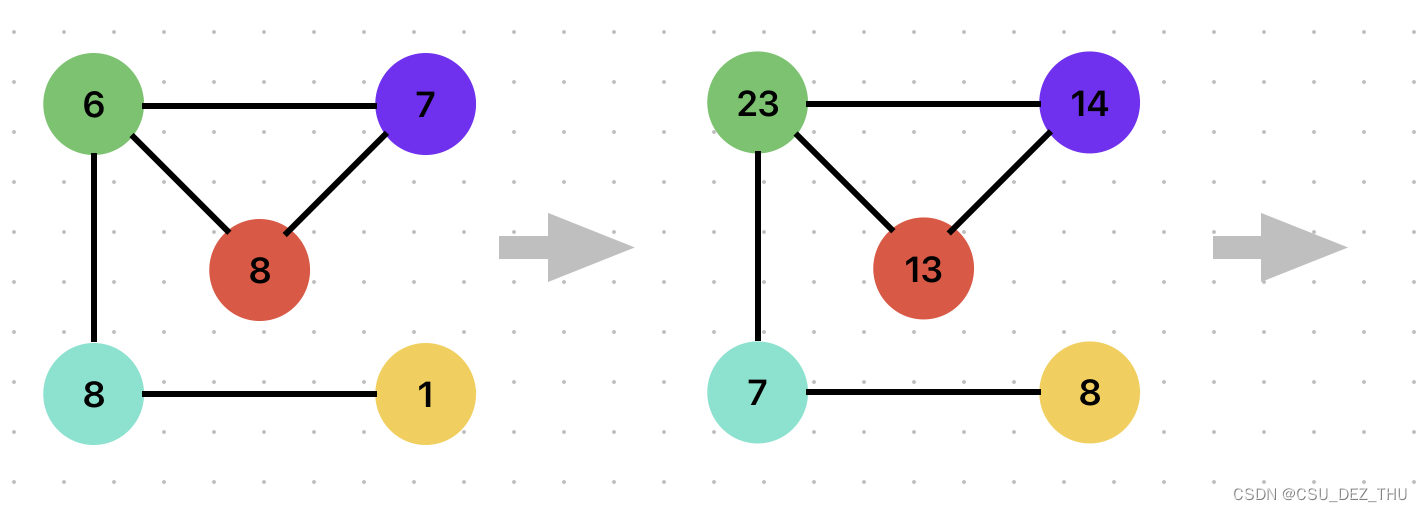
单纯看公式会觉得不好理解,结合具体的例子可以马上掌握,它在本质上是求图 G 邻接矩阵的特征向量,只不过在算法设计中,通常不是通过数学方式求得,而是采用迭代逼近的方式得到一个近似解。特征向量中心性的核心思想是,一个结点的邻居越重要,该结点就越重要。下面是一个经典的分析图,

各节点上的数字表示该结点的权重,以 5 作为节点 1,按顺时针标记各节点,且中心节点记为节点 5,则得到邻接矩阵为
第一轮迭代,邻接矩阵乘上各结点的分数
迭代完成后,各结点分数发生变化,效果为节点“吸收”了邻接节点的分数,邻接节点分数高的,迭代后分数就高。且经过多轮迭代后,各节点间的相对分数将不再发生变化,即收敛,仅存在绝对分数的缩放,此时我们就得到了最终的中心性分数矩阵,而该矩阵是邻接矩阵的特征向量。
二、katz 中心性
针对特征向量中心性无法用于有向图的不足,提出了 katz 中心性。
2.1 理解特征向量中心性的不足
每篇博客都说了,特征向量中心性不能用于有向图,但是为什么呢,这个结论怎么来的?
此处稍微探究下,我的理解不一定是对的,但特征向量中心性确实存在一些问题。首先观察上一节中邻接矩阵的特点,它是沿着主对角线对称的矩阵。这是可以理解的,无向图的连通性肯定是对称的。而特征向量中心性算法的本质是求邻接矩阵的特征向量,当邻接矩阵的性质发生变化时,特征向量必然会受影响。
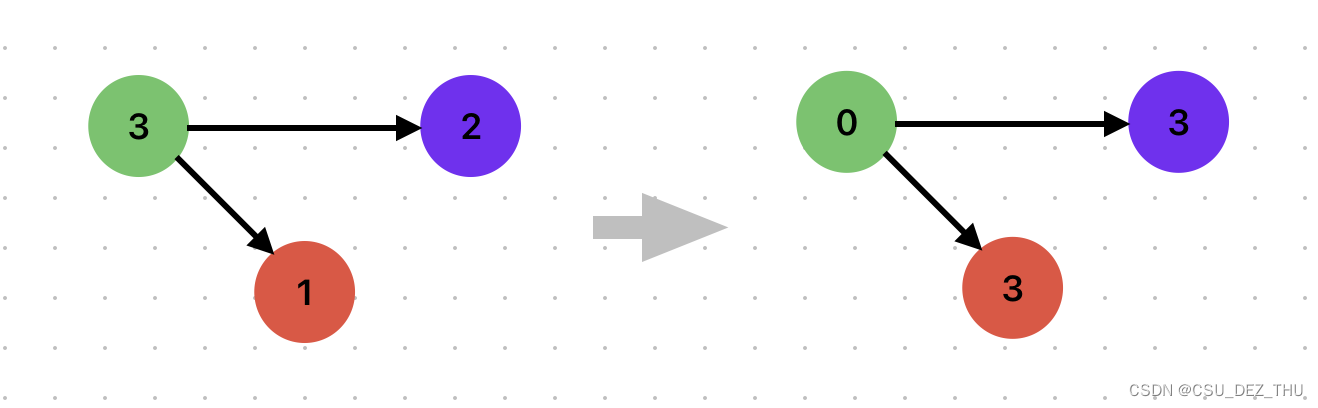
在有向图中没有沿主对角线对称这一性质,那么对于只有出度、没有入度的节点,就存在一个致命问题,它的分数一直被出度节点吸收,而它自身分数将归零(以下图为例)。这显然是不合理的,这也是我理解的特征向量中心性计算方式不足的原因。
2.2 katz 中心性的改进思路
首先看看它的中心性计算公式,
.
比较和特征向量中心性的不同,katz 引入了两个新的变量,分别是衰减因子 和基本偏移量
。第一个求和号中的 k 表示 k-hop,即只考虑与节点 v 距离在 k 以内(通常以一个节点作为一个单位距离)的节点分数,该思路在特征向量中心性中也是可行的,只是在上一节中未列出来。
- 衰减因子
随着 k 增大呈指数级减小,其设计思路是距离越近的节点对分数的影响应更大,反之应有衰减;
- 偏移量
是为了避免出现 2.1 中讨论的分数归零现象;
可能较难理解,其实就是在 k 距离内的邻接矩阵,如 k = 1 就是与节点 v 直接相连的邻接矩阵,k = 2 就是与节点 v 隔一个节点相连的邻接矩阵。
通过例子理解先跳过,可以自己搜索具体的计算例子。
三、PageRank 中心性(PageRank centrality)
PageRank 应该是这三者中最出名的,主要用于谷歌的网页排序。
3.1 PageRank 中心性思想
相关文章:
【图论】三种中心性 —— 特征向量、katz 和 PageRank
维基百科:在图论和网络分析中,中心性指标为图中相应网络位置的节点分配排名或数值。中心性这一概念最初起源于社交网络分析,因此很多衡量中心性的术语也反映了其社会学背景。 不同中心性指标对 “重要” 的衡量方式不同,因此适用于…...

[sqoop]将hive查询后的数据导入到MySQL
一、知识点 export:将Hive的表导入到mysql叫导出 搜了很多,发现sqoop在hive导出到mysql时 1)不支持where参数对数据进行过滤。 2)不支持指定hive表的方式导出,只能指定Hive目录进行导出。 二、操作 1、在MySQL中建表 creat…...

Linux df、du命令
df:查看文件系统硬盘使用情况 df 命令,用于显示 Linux 系统中各文件系统的硬盘使用情况,包括文件系统所在硬盘分区的总容量、已使用的容量、剩余容量等。 df 命令的基本格式为: [rootlocalhost ~]# df [选项] [目录或文件名] df…...
java版+免费商城搭建+小程序商城免费搭建+Spring Cloud + Spring Boot + MybatisPlus + 前后端分离 + 二次开发
J2EE企业分布式微服务云快速开发架构 Spring CloudSpring Boot2MybatisOauth2ElementUI 前后端分离 1. 鸿鹄Cloud架构清单 2. Commonservice(通用服务) 通用服务:对spring Cloud组件的使用&封装,是一套完整的针对于分布式微…...
软件设计师学习第一章
计算机组成与体系结构(6分) 内容概述 数据的表示 进制转换 R 进制转十进制使用按权展开法,其具体操作方式为:将 R 进制数的每一位数值用 Rk 形示,即幂的底数是 R ,指数为 k , k 与该位和小数点…...

蓝桥杯单片机第十一届国赛 真题+代码
iic.c /* # I2C代码片段说明1. 本文件夹中提供的驱动代码供参赛选手完成程序设计参考。2. 参赛选手可以自行编写相关代码或以该代码为基础,根据所选单片机类型、运行速度和试题中对单片机时钟频率的要求,进行代码调试和修改。 */ #include <STC1…...

IDC报告背后:大模型时代,重新理解AI公有云
大模型之于AI公有云的意义,在于大模型可以改变过去“手工作坊定制算法”的高成本模式,转向“工厂模式”,只需要微调和精调,就可以形成针对性的场景算法。 作者|葛覃 出品|产业家 一年前,依然有不少云计算从业者思…...

UNH-IOL Reservation 一致性测试用例【7】- 清除Reservation
Reservation 系列导航 UNH-IOL Reservation 一致性测试用例【1】- Reservation Report 命令验证 UNH-IOL Reservation 一致性测试用例【2】- Reservation注册 UNH-IOL Reservation 一致性测试用例【3】- 取消注册 UNH-IOL Reservation 一致性测试用例【4】- Reservation Acqui…...

Python 生成随机图片验证码
使用Python生成图片验证码 Python 生成随机图片验证码安装pillow包pillow包生成图片基本用法生成图片验证码 Python 生成随机图片验证码 在写一个Web项目的时候一般要写登录操作,而为了安全起见,现在的登录功能都会加上输入图片验证码这一功能ÿ…...

一些有趣的 js 功能函数
一些有趣的 js 功能函数 数组生成数组打乱数组数组简单数据去重数组唯一值数据去重多数组取交集查找最大值索引查找最小值索引找到最接近的数值压缩多个数组(拉链函数)矩阵交换行和列 数字转换进制转换 正则手机号格式化去除多余空格 web重新加载当前页面…...
摄像头m2dock(MAIX-II DOCK)
官方文档地址 https://wiki.sipeed.com/soft/maixpy3/zh/index.html 一、软件准备 1 烧录镜像软件 2 镜像 当前最近版本镜像文件 3 SDFormatter 4 Maixpy IDE 二、SD卡准备 1 格式化SD卡(用SDFormatter) 2 烧录 3 弹出,插入开发板中 出现…...

SpringBoot 如何优雅的进行全局异常处理
在SpringBoot的开发中,为了提高程序运行的鲁棒性,我们经常需要对各种程序异常进行处理,但是如果在每个出异常的地方进行单独处理的话,这会引入大量业务不相关的异常处理代码,增加了程序的耦合,同时未来想改…...

OSPF路由协议(红茶三杯CCNA)
链路状态路由协议 OSPF(开放式最短路径优先)Open Shortest Path First 是一种链路状态路由协议,无路由循环(全局拓扑),RFC2328 “开放”意味着非私有的 管理型距离:110 OSPF采用SPF算法计算到达…...
redis中使用bloomfilter判断元素是否存在
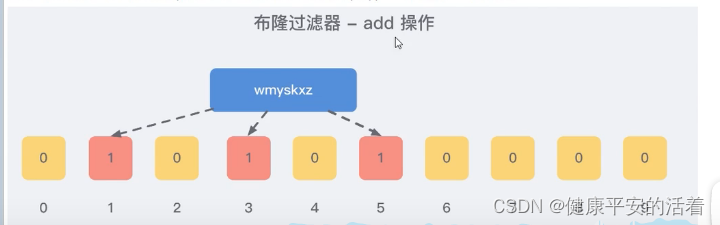
一 bloomfiler的作用 1.1 bloomfilter的作用 由一个初始值为0的bit数组组成,和多个hash函数构成,用来判断集合中是否存在某个元素。 一个很长的二进制数组(00000000)一系列随机hash算法映射函数。主要用于判断一个元素是否存在…...

互联网医院系统源码实现:打造现代化医疗服务平台
摘要 本文将介绍一个基于Python的简化版互联网医院系统的源码实现,主要包含用户注册与登录、医生信息管理、在线预约挂号、在线问诊与咨询、电子病历管理、在线支付与结算等功能。该源码实现仅为示例,实际开发中需要考虑更多的业务逻辑和安全性。 1. …...
每天100w次登陆请求, 8G 内存该如何设置JVM参数?
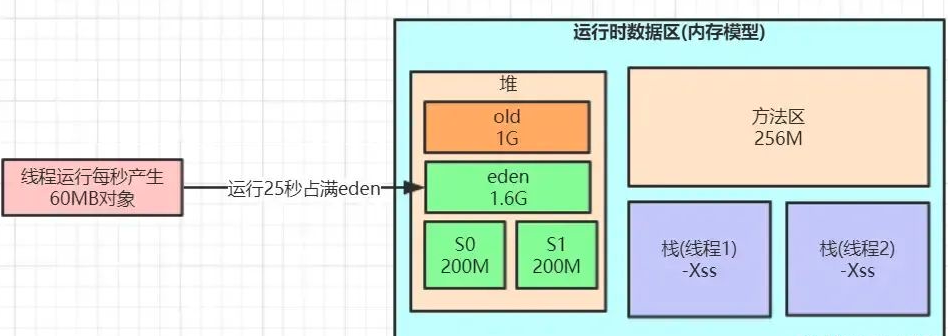
一、新系统上线如何规划容量? 1.套路总结 任何新的业务系统在上线以前都需要去估算服务器配置和JVM的内存参数,这个容量与资源规划并不仅仅是系统架构师的随意估算的,需要根据系统所在业务场景去估算,推断出来一个系统运行模型&…...

Fiddler Everywhere(TTP调试抓包工具) for Mac苹果电脑版
Fiddler Everywhere for Mac版是Mac电脑上的一款跨平台的HTTP调试抓包工具,Fiddler Everywhere for Mac能够记录客户端与服务器之间的所有HTTP(S)通信,支持对包进行监视、分析、设置断点、甚至修改请求/响应数据等操作。 适用于任…...

Paragon NTFS2023最新版Mac读写NTFS磁盘工具
Paragon NTFS for Mac是Mac平台上一款非常优秀的读写工具,可以在Mac OS X中完全读写、修改、访问NTFS硬盘、U盘等外接设备的文件。这款软件最大的亮点简书可以让我们读写 NTFS 分区,因为在Mac OS X 系统上,默认状态下我们只能读取NTFS 分区&a…...
vs2013 32位 编译的 dll,重新用vs2022 64位编译,所遇问题记录
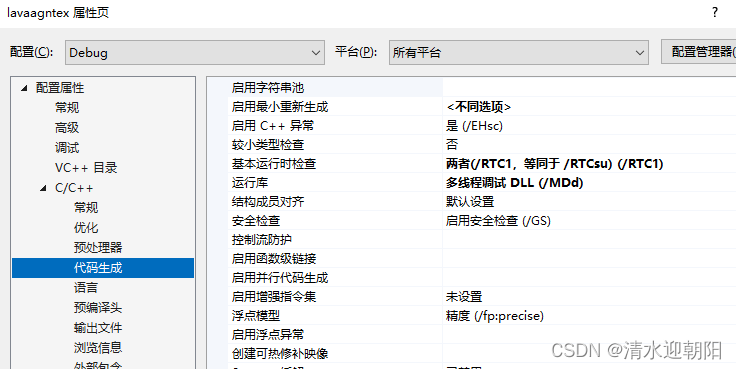
目录 一、vs2013 32 DLL 转 VS2022 64 DLL 所遇问题 1、 LNK2038: 检测到“_MSC_VER”的不匹配项: 值“1800”不匹配值“1900” 2、原先VS2013 现在 VS2022 导致的vsnprintf 重定义问题 3、 无法解析的外部符号 __vsnwprintf_s 4、无法解析的外部符号__imp__CertFreeC…...
Linux_CentOS_7.9部署Docker以及镜像加速配置等实操验证全过程手册
前言:实操之前大家应该熟悉一个新的名词DevOps 俗称开发即运维、新一代开发工程师(Development和Operations的组合词)是一组过程、方法与系统的统称,用于促进开发(应用程序/软件工程)、技术运营和质量保障&…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
