【每日一题】2569. 更新数组后处理求和查询
【每日一题】2569. 更新数组后处理求和查询
- 2569. 更新数组后处理求和查询
- 题目描述
- 解题思路
2569. 更新数组后处理求和查询
题目描述
给你两个下标从 0 开始的数组 nums1 和 nums2 ,和一个二维数组 queries 表示一些操作。总共有 3 种类型的操作:
操作类型 1 为 queries[i] = [1, l, r] 。你需要将 nums1 从下标 l 到下标 r 的所有 0 反转成 1 以及所有 1 反转成 0 。l 和 r 下标都从 0 开始。
操作类型 2 为 queries[i] = [2, p, 0] 。对于 0 <= i < n 中的所有下标,令 nums2[i] = nums2[i] + nums1[i] * p 。
操作类型 3 为 queries[i] = [3, 0, 0] 。求 nums2 中所有元素的和。
请你返回一个数组,包含所有第三种操作类型的答案。
示例 1:
输入:nums1 = [1,0,1], nums2 = [0,0,0], queries = [[1,1,1],[2,1,0],[3,0,0]]
输出:[3]
解释:第一个操作后 nums1 变为 [1,1,1] 。第二个操作后,nums2 变成 [1,1,1] ,所以第三个操作的答案为 3 。所以返回 [3] 。
示例 2:
输入:nums1 = [1], nums2 = [5], queries = [[2,0,0],[3,0,0]]
输出:[5]
解释:第一个操作后,nums2 保持不变为 [5] ,所以第二个操作的答案是 5 。所以返回 [5] 。
提示:
1 <= nums1.length,nums2.length <= 105
nums1.length = nums2.length
1 <= queries.length <= 105
queries[i].length = 3
0 <= l <= r <= nums1.length - 1
0 <= p <= 106
0 <= nums1[i] <= 1
0 <= nums2[i] <= 109
解题思路
思路1:最直观的想法是,暴力模拟。(很显然超时)
class Solution {
public:vector<long long> handleQuery(vector<int>& nums1, vector<int>& nums2, vector<vector<int>>& queries) {vector<long long> res;for(auto query:queries){int a=query[0];int b=query[1];int c=query[2];switch(a){case 1:for(int i=b;i<=c;i++)nums1[i]=!nums1[i];break;case 2:for(int i=0;i<nums2.size();i++)nums2[i]+=nums1[i]*b;break;case 3:long long sum=accumulate(nums2.begin(),nums2.end(),0.0);res.push_back(sum); }}return res;}};
思路2:涉及到区间修改以及区间查询,一般使用线段树。线段树将每个长度不为 1 的区间划分成左右两个区间递归求解,把整个线段划分为一个树形结构,通过合并左右两区间信息来求得该区间的信息。线段树每个节点有一个编号i,其表示区间[l,r]的元素和,该元素左节点有一个编号2*i,其表示区间[l,m]的元素和,该元素右节点有一个编号2*i+1,其表示区间[m+1,r]的元素和,其中m=l+(r-l)/2。其中我们可以给每个节点加上标记tag,当修改时修改当前tag和区间和,等到下次查询时再将tag下放。
class Solution {
public://节点个数 最多4nstatic constexpr int MX=4e5+1;//区间1的个数int cnt1[MX];//整个区间是否需要翻转标记bool flip[MX];//维护区间1的个数void maintain(int o){//当前节点对应区间的1的数量等于左右孩子对应区间1的个数cnt1[o]=cnt1[2*o]+cnt1[2*o+1];}//执行区间翻转 o为当前节点下标 [l,r]为区间void do_(int o,int l,int r){//区间长度减去原本1的个数即原本0的个数即翻转后1的个数cnt1[o]=r-l+1-cnt1[o];flip[o]=!flip[o];}//初始化线段树 o是节点标记 从1开始 但是数组下标从0开始void build(vector<int>&a,int o,int l,int r){//只有一个元素直接求和if(l==r){cnt1[o]=a[l-1];return;}//分成区间求和int m=l+(r-l)/2;//左孩子标记为o*2 左区间为[l,m]build(a,o*2,l,m);//右孩子标记为o*2+1 右区间为[m+1,r]build(a,o*2+1,m+1,r);//该节点区间和为左右孩子区间和之和maintain(o);}//翻转区间 当前标记为o 当前区间为[l,r] 当前待更新区间为[L,R] void update(int o,int l,int r,int L,int R){//[L,R]在[l,r]内部if(L<=l&&r<=R){do_(o,l,r);return;}//分而治之int m=l+(r-l)/2;//如果有标记则需要向下传递标记并且清空当前节点之前的标记情况if(flip[o]){do_(o*2,l,m);do_(o*2+1,m+1,r);flip[o]=false;}//左区间有交集if(m>=L)update(o*2,l,m,L,R);//右区间有交集if(m<R)update(o*2+1,m+1,r,L,R);//该节点区间和为左右孩子区间和之和maintain(o);}vector<long long> handleQuery(vector<int>& nums1, vector<int>& nums2, vector<vector<int>>& queries) {int n=nums1.size();build(nums1,1,1,n);vector<long long> res;long long sum=accumulate(nums2.begin(),nums2.end(),0LL);for(auto q:queries){if(q[0]==1)update(1,1,n,q[1]+1,q[2]+1);else if(q[0]==2)sum+=1LL*q[1]*cnt1[1];elseres.push_back(sum);}return res;}
};
总结:https://oi-wiki.org/ds/seg/讲得很好!!
相关文章:

【每日一题】2569. 更新数组后处理求和查询
【每日一题】2569. 更新数组后处理求和查询 2569. 更新数组后处理求和查询题目描述解题思路 2569. 更新数组后处理求和查询 题目描述 给你两个下标从 0 开始的数组 nums1 和 nums2 ,和一个二维数组 queries 表示一些操作。总共有 3 种类型的操作: 操作…...
PLC的高端版本通常具有以下特点:
高速处理能力:高端PLC通常具有更快的处理速度和更高的运行频率,可以处理更复杂的控制逻辑和更多的输入/输出信号。 大容量存储:高端PLC通常具有更大的存储容量,可以保存更多的程序和数据,以满足更复杂的应用需求。 多种…...

Scrum敏捷开发项目管理和产品研发管理培训- Leangoo领歌
Scrum是目前运用最为广泛的敏捷开发方法,是一个轻量级的项目管理和产品研发管理框架。 这是一个两天的实训课程,面向研发管理者、项目经理、产品经理、研发团队等,旨在帮助学员全面系统地学习Scrum和敏捷开发, 帮助企业快速启动敏捷实施。 …...

爬虫小白-如何辨别是否有cookie反爬案例
目录 一、Cookie介绍二、cookie生成来源区分查找三、如何判断是否有cookie反爬四、来自服务器生成的cookie反爬解决方法五、来自js生成的cookie反爬解决方法一、Cookie介绍 先推荐该篇文章简单了解Cookie、Session、Token、JWT1、cookie的类型:会话cookie和持久cookie;其唯一…...

机器人状态估计:robot_localization 功能包简介与安装
机器人状态估计:robot_localization 功能包简介与参数配置 前言功能包简介安装使用ubuntu软件源安装使用源码安装 前言 移动机器人的状态估计需要用到很多传感器,因为对单一的传感器来讲,都存在各自的优缺点,所以需要一种多传感器…...
RNN架构解析——GRU模型
目录 GRU模型实现优点和缺点 GRU模型 实现 优点和缺点...

【LeetCode】141.环形链表
题目 给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置&#…...
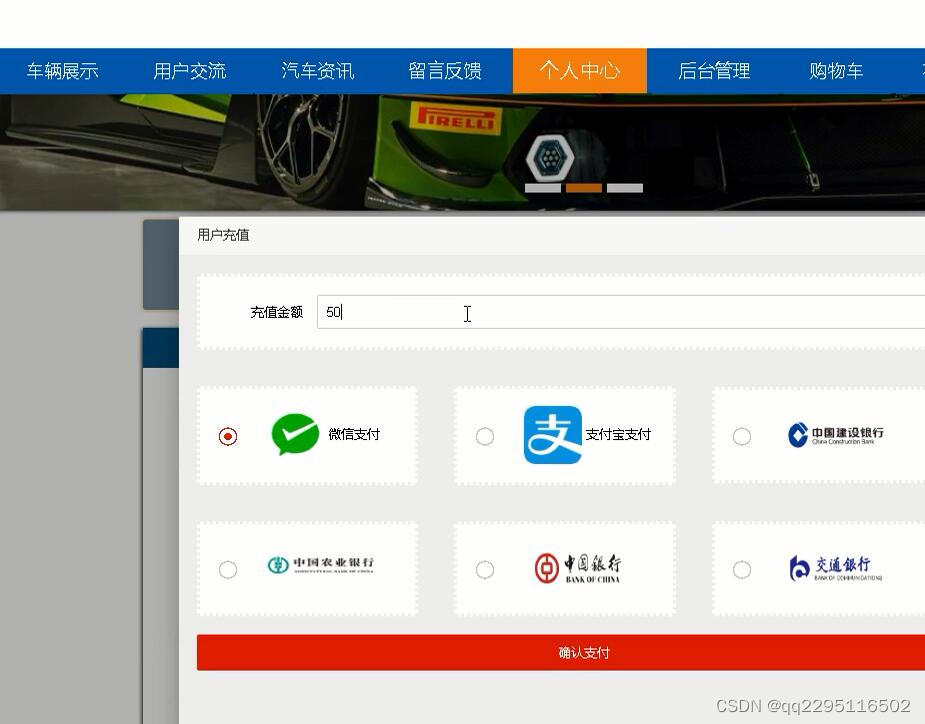
nodejs+vue+elementui汽车销售网站
前端技术:nodejsvueelementui,视图层其实质就是vue页面,通过编写vue页面从而展示在浏览器中,编写完成的vue页面要能够和控制器类进行交互,从而使得用户在点击网页进行操作时能够正常。 可以设置中间件来响应 HTTP 请求。 Express …...

spring boot整合kaptcha验证码
引入依赖 <dependency><groupId>com.github.penggle</groupId><artifactId>kaptcha</artifactId><version>2.3.2</version> </dependency>创建验证码生成配置类 KaptchaConfig.java Configuration public class KaptchaConf…...

【Linux下6818开发板(ARM)】在液晶屏上显示RGB颜色和BMP图片
(꒪ꇴ꒪ ),hello我是祐言博客主页:C语言基础,Linux基础,软件配置领域博主🌍快上🚘,一起学习!送给读者的一句鸡汤🤔:集中起来的意志可以击穿顽石!作者水平很有限,如果发现错误&#x…...

React的hooks---useLayoutEffect
useLayoutEffect 与 useEffect 类似,与 useEffect 在浏览器 layout 和 painting 完成后异步执行 effect 不同的是,它会在浏览器布局 layout 之后,painting 之前同步执行 effect useLayoutEffect 的执行时机对比如下: import Rea…...

北京创业孵化器汇总
北京创业孵化器汇总 1 创客总部实验室技术孵化平台 人工智能 海淀区中关村大街18号B座0909室 2 中孵高科 医药健康 经济技术开发区科创十四街99号D座9层 3 九州众创孵化器 医药健康 大兴区广平大街9号6幢等2幢 4 北京大学人工智能产业化孵化平台 国家级/市级 人工智能 中关村…...

电信软件的过去、现在和未来:推动核心网发展的关键力量
目录 导语:过去:从基础功能到增强服务现在:软件定义网络和智能化运营SDNNFV 未来:5G和物联网的挑战与机遇结束语 导语: 电信软件是支撑电信核心网运营的重要组成部分,它们在过去几十年中经历了巨大的变革。…...

2023年全国程序员薪酬排行天梯榜
文章目录 ⭐️ 2023年全国程序员薪酬排行天梯榜 在过去很长的一段时间内,网上总有一个声音:“大厂裁员”、“程序员内卷严重”、“程序员人员过盛”、“35岁中年危机”、“码农吃的青春饭”、“互联网寒冬” 等等等等。 讲道理,我对这种人为的…...

设计模式-工厂模式
定义 工厂模式是用来创建对象的一种最常用的设计模式,不暴露创建对象的具体逻辑,而是将将逻辑封装在一个函数中,那么这个函数就可以被视为一个工厂 其就像工厂一样重复的产生类似的产品,工厂模式只需要我们传入正确的参数&#…...
HummerRisk V1.3.0 发布
HummerRisk V1.3.0发布: 大家好,HummerRisk 1.3.0和大家见面了,在这个版本中我们继续在多云接入管理、多云检测方式、云资源态势方面提供新的能力,并增加了新的镜像仓库支持类型,并优化了云的区域选择、优化规则组内容…...
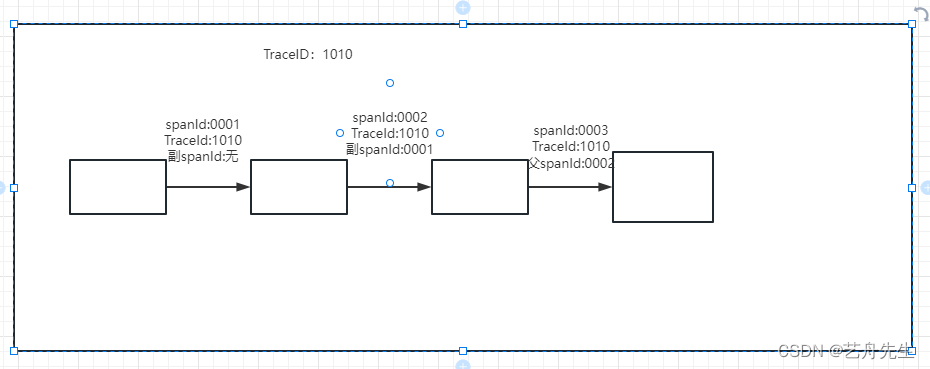
SkyWalking链路追踪中Trace概念以及Trace与span的关系
基本概念 在SkyWalking链路追踪中,Trace(追踪)是指一个请求或者一个操作从开始到结束的完整路径。它涵盖了分布式系统中所有相关组件的调用关系和性能信息。 具体来说,Trace包含了一系列的span(跨度)&…...
美容店预约小程序制作教程详解
现在,制作一个专属于美容店的预约小程序不再需要编程经验,通过乔拓云网提供的后台管理系统,你可以轻松地完成整个制作过程。下面,我将为你详细介绍如何DIY一个美容店预约小程序。 首先,登录乔拓云网的后台管理系统&…...

什么是内存泄漏及如何防护内存泄漏
目录 前言 什么是内存泄漏示例一示例二特殊版本 总结/结尾 前言 最近阅读量很低啊( ≧Д≦) 什么是内存泄漏 内存泄漏(Memory Leak)指在程序运行过程中,分配的内存空间在不再使用后未被正确释放或回收,导致这部分内存…...

【libuv】httpserver启用ssl 及 播放的日志打印
VLC vlc 第一次 接收不安全的证书黑屏。重启服务,再次vlc这次次好像就可以了。main debug: processing request item: zhangbin.flv, node: 播放列表, skip: 0 main debug: rebuilding array of current - root 播放列表 main debug: rebuild done - 2 items, index 1 main de…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
