算法训练营DAY54|583. 两个字符串的删除操作、72. 编辑距离
583. 两个字符串的删除操作 - 力扣(LeetCode)![]() https://leetcode.cn/problems/delete-operation-for-two-strings/这道题也是对于编辑距离的铺垫题目,是可以操作两个字符串的删除,使得两个字符串的字符完全相同,这道题可以用递推公式模拟删除,也可以使用求两个字符串的最大公共子序列的解题方法,求出最长的公共非连续子序列,然后再用两个字符串本身的长度减去这个公共子序列长度,也可以求出至少要删除几步。这里只分析第一种解题方法。
https://leetcode.cn/problems/delete-operation-for-two-strings/这道题也是对于编辑距离的铺垫题目,是可以操作两个字符串的删除,使得两个字符串的字符完全相同,这道题可以用递推公式模拟删除,也可以使用求两个字符串的最大公共子序列的解题方法,求出最长的公共非连续子序列,然后再用两个字符串本身的长度减去这个公共子序列长度,也可以求出至少要删除几步。这里只分析第一种解题方法。
dp数组的含义:dp【i】【j】表示以i-1为下标的字符串1和以j-1为结尾的字符串2,要想使它们相等,所要删除的最小步数是多少。
递推公式:由于dp数值含义,当字符串1的i-1为结尾的下标元素,与字符串2以j-1为结尾的下标元素相等时,dp【i】【j】=dp【i-1】【j-1】。含义是当前元素相等,那么到达当前的位置需要删除的步数就和上一个位置的所需步数相等,因为此时元素相等,没有删除元素。
第二种情况就是两个对应元素不相等,这时又分为两种不同情况,即两元素不等的时候,删除第一个字符串的元素,或者是删除第二个字符串的元素,比较一下当前是哪一种删除的步数可以得到最小值。第一种就是删除字符串1的那个字符,那就是dp【i-1】【j】+1,dp数组的定义是i-1和j-1的下标的,所以此时j就代表前一个字符不变,然后略过字符串1这个字符,去向前找上一次的删除步数是多少,第二种情况是删除字符串2自然就是,dp【i】【j-1】+1,最后取最小值。
dp数组初始化:初始化一般是看递推公式决定的,当字符串1为空时候,字符串2需要删除当前字符个数的步数才能达到空字符串也就是需要删除j个。当字符串2为空也是同样的道理,字符串1需要删除i个。根据这一性质我们可以初始化第一行和第一列,也就是两个分别是空字符串情况,其他的部分统一初始化为0因为递推公式会全部覆盖。
遍历顺序:根据递推公式可知,从上到下,从左到右。
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>>dp(word1.size()+1,vector<int>(word2.size()+1,0));dp[0][0]=0;for(int i=1;i<=word1.size();i++)dp[i][0]=i;for(int j=1;j<=word2.size();j++)dp[0][j]=j;for(int i=1;i<=word1.size();i++){for(int j=1;j<=word2.size();j++){if(word1[i-1]==word2[j-1])dp[i][j]=dp[i-1][j-1];else dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1);}}return dp[word1.size()][word2.size()];}
};72. 编辑距离 - 力扣(LeetCode)![]() https://leetcode.cn/problems/edit-distance/
https://leetcode.cn/problems/edit-distance/
编辑距离是一道困难题,有了前面几期的铺垫,这道题也能更容易理解一些,这道题是求使两个字符串能变相等的最小操作数有几步,题目要求可以使任意一个字符串增加一个字符,或删除一个字符,或替换该指定位置的字符,看起来题目要求有一些复杂,但是实际上还是较容易理解的,主要是要弄懂递推公式的意义是什么。
dp数组的含义:dp数组的含义是到第一个字符串i-1的位置和第二个字符串j-1位置为止,所用最少的步数能使它们相等。
递推公式:我们来看如果两对应下标字符对应相等,那么就应该是当前的位置最少步数,等于上一次对应下标的最少步数。
if(word1【i-1】==word2【j-1】dp【i】【j】=dp【i-1】【j-1】
如果两对应下标字符不等,那么我们先来分析删除字符
根据往期的删除字符的操作,即是当两个字符确认已经不等时候,要么是不考虑字符1当前的字符而去考虑前一个位置,要么就是不考虑字符2的当前字符,去考虑它的前一个字符。然后取最小值。也就是dp【i-1】【j】和dp【i】【j-1】两者取最小值。那么增加字符怎么写呢?这是关键,实际上增加字符是和删除字符的递推公式是完全一样的。因为我们删除了字符串1的一个字符,不就是相当于增加了字符串2的一个字符吗?我们要增加的字符一定是我们所需要的字符,也就是字符串2里没有的但是字符串1里有的,反之同理,所以说它们的操作本质上是一样的。那么还剩下最后一种情况,就是交换两个字符串,word1替换word1【i-1】或者word2替换word2【j-1】才能使两字符串相等,回顾一下如果这两个字符相同的话,那么在dp数组应表现为dp【i】【j】=dp【i-1】【j-1】,所以当他们不同,而且此时又不是增删操作时候,我们替换其中一个字符所用的最少步数应该是dp【i-1】【j-1】+1。也就是说替换一个字符就可以让word1【i-1】和word2【j-1】相等。根据上面的推理,我们得出结论,递推公式就是他们三种情况取最小的方案。
dp数组的初始化:dp数组初始化与上一道题思路是相同的,当一个串是空串时,那么另一个串就需要删除全部字符,才能与之相等,按照这一思路来初始化。
遍历顺序:由递推公式可知,遍历顺序是从左到右,从上到下的。
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>>dp(word1.size()+1,vector<int>(word2.size()+1,0));for(int i=0;i<=word1.size();i++)dp[i][0]=i;for(int j=0;j<=word2.size();j++)dp[0][j]=j;for(int i=1;i<=word1.size();i++){for(int j=1;j<=word2.size();j++){if(word1[i-1]==word2[j-1])dp[i][j]=dp[i-1][j-1];else dp[i][j]=min(dp[i-1][j-1]+1,min(dp[i-1][j]+1,dp[i][j-1]+1));}}return dp[word1.size()][word2.size()];}
};重要的是要理清递推公式的思想,其他的部分和以往做的题没有什么太大区别,即使它是一道困难题。
相关文章:
算法训练营DAY54|583. 两个字符串的删除操作、72. 编辑距离
583. 两个字符串的删除操作 - 力扣(LeetCode)https://leetcode.cn/problems/delete-operation-for-two-strings/这道题也是对于编辑距离的铺垫题目,是可以操作两个字符串的删除,使得两个字符串的字符完全相同,这道题可…...

【Ctfshow_Web】信息收集和爆破
0x00 信息收集 web1 直接查看源码 web2 查看不了源码,抓包即可看到(JS拦截了F12) web3 抓包,发送repeater,在响应包中有Flag字段 web4 题目提示后台地址在robots,访问/robots.txt看到Disallow: /fl…...

基于机器学习的推荐算法研究与实现
摘要随着互联网的普及,人们可以通过搜索引擎、社交网络等方式获取大量的信息资源。但是,面对如此之多的信息,人们往往会感到迷失和困惑,无法快速准确地找到自己需要的信息。在这种情况下,推荐算法的出现为我们提供了一…...
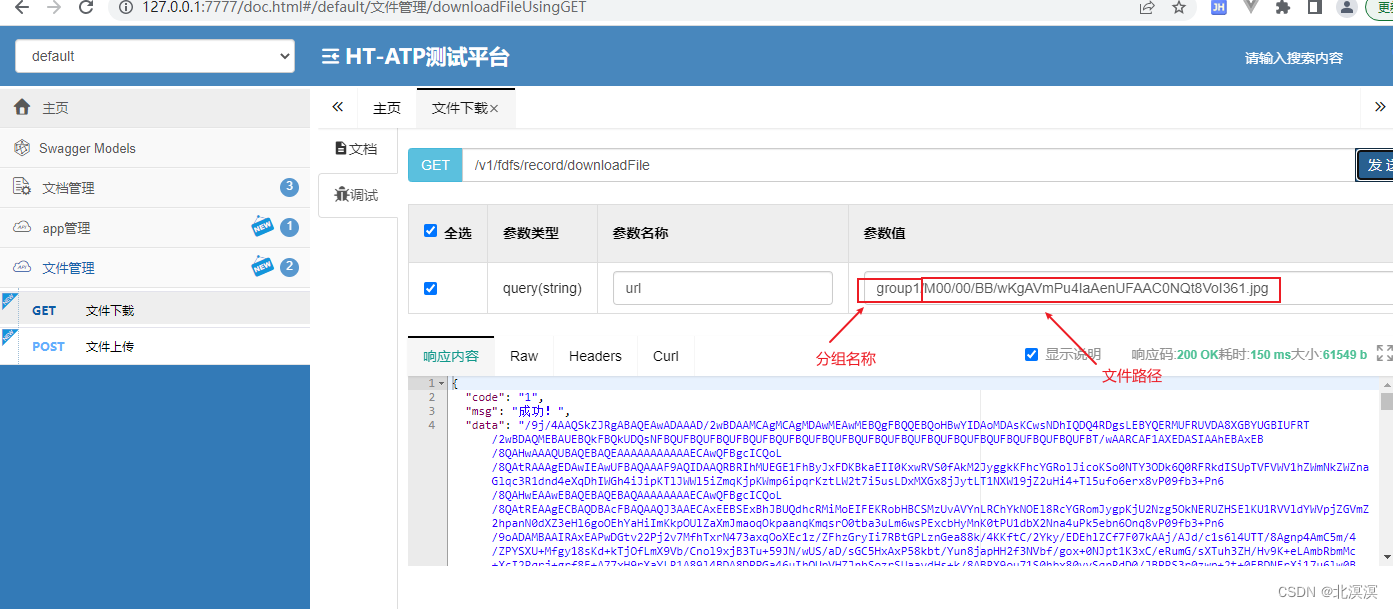
(二十四)ATP应用测试平台——springboot集成fastdfs上传与下载功能
前言 本节内容我们主要介绍一下如何在springboot项目中集成fastdfs组件,实现文件的上传与下载。关于fastdfs服务中间键的安装过程,本节内容不做介绍。fastdfs是一个轻量级的分布式文件系统,也是我们文件存储中常常使用的组件之一,…...

linux好用命令+vs快捷键
linux好用命令 功能指令跳转到vim界面的最后一行shift键g复制当前路径下所有文件和目录(加-r才行)到target目录cp -r * /home/target删除指定文件rm -rf test.txt文件重命名(-i交互式提示)mv -i file1 file2移动某个内容…...

Git 构建分布式版本控制系统
版本控制概念Gitlab部署1.版本控制概念 1.1分类 (一)1 本地版本控制系统(传统模式) (二)2 集中化的版本控制系统 CVS、Subversion(SVN) (三)3 分布式…...
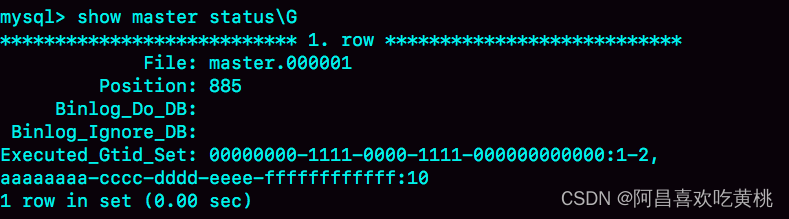
Day891.一主多从的切换正确性 -MySQL实战
一主多从的切换正确性 Hi,我是阿昌,今天学习记录的是关于一主多从的切换正确性的内容。 在切换任务的时候,要先主动跳过这些错误,通过主动跳过一个事务或者直接设置跳过指定的错误,用GTID解决找同步位点的问题 大多…...
【论文笔记】图像修复Learning Joint Spatial-Temporal Transformations for Video Inpainting
论文地址:https://arxiv.org/abs/2007.10247 源码地址:GitHub - researchmm/STTN: [ECCV2020] STTN: Learning Joint Spatial-Temporal Transformations for Video Inpainting 一、项目介绍 当下SITA的方法大多采用注意模型,通过搜索参考帧…...
代码随想录算法训练营第二天 | 977.有序数组的平方 、209.长度最小的子数组 、59.螺旋矩阵II、总结
打卡第二天,认真做了两道题目,顶不住了好困,明天早上练完车回来再重新看看。 今日任务 第一章数组 977.有序数组的平方209.长度最小的子数组59.螺旋矩阵II 977.有序数组的平方 给你一个按 非递减顺序 排序的整数数组 nums,返回 每…...

Python pickle模块:实现Python对象的持久化存储
Python 中有个序列化过程叫作 pickle,它能够实现任意对象与文本之间的相互转化,也可以实现任意对象与二进制之间的相互转化。也就是说,pickle 可以实现 Python 对象的存储及恢复。值得一提的是,pickle 是 python 语言的一个标准模…...
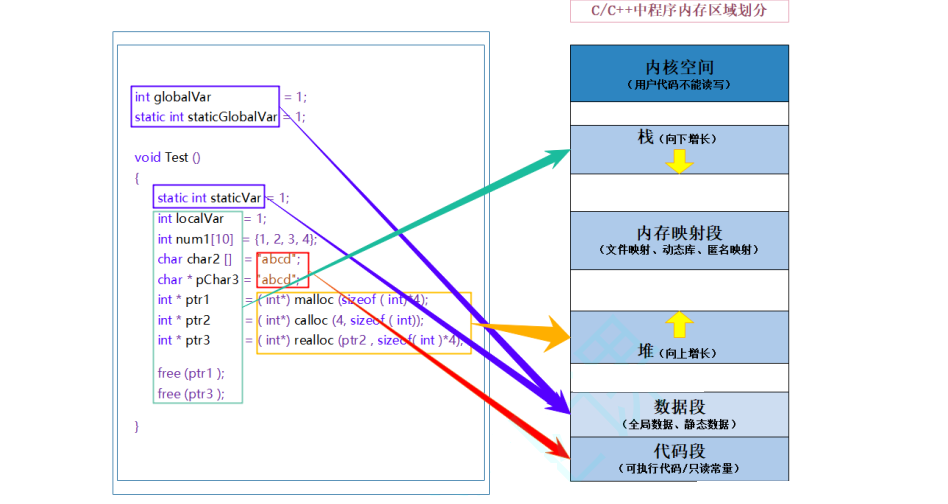
【C++】C/C++内存管理
文章目录1. C/C内存分布2. C语言当中的动态内存管理3. C 内存管理方式3.1 new/delete操作内置类型3.2 new和delete操作自定义类型4. operator new 和operator delete 函数5. new和delete的实现原理5.1 内置类型5.2 自定义类型6. 定位new表达式(placement-new)7. 常见面试题7.1 …...

【测试】自动化测试02
努力经营当下,直至未来明朗! 文章目录前言 回顾 预告一、常见的元素操作1. 输入文本sendKeys()2. 点击click3. 提交submit(通过回车键提交)4. 清除clear5. 获取文本getText()6. 获取属性对应的值getAttribute()7. 查看title和ur…...
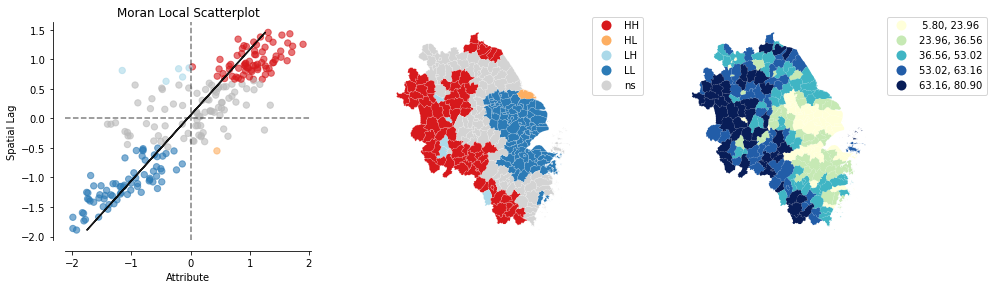
Python空间分析| 02 利用Python计算空间局部自相关(LISA)
局部空间自相关 import esda import numpy as np import pandas as pd import libpysal as lps import geopandas as gpd import contextily as ctx import matplotlib.pyplot as plt from geopandas import GeoDataFrame from shapely.geometry import Point from pylab im…...

idea快捷编码:生成for循环、主函数、判空非空、生成单例方法、输出;自定义快捷表达式
前言 idea可根据输入的简单表达式进行识别,快速生成语句 常用的快捷编码:生成for循环、主函数、判空非空、生成单例方法、输出 自定义快捷表达式 博客地址:芒果橙的个人博客 【http://mangocheng.com】 一、idea默认的快捷表达式查看 Editor…...

【Spring】@Value注入配置文件 application.yml 中的值失败怎么办
本期目录一、 问题背景二、 问题原因三、 解决方法一、 问题背景 今天碰到的问题是用 Value 注解无法注入配置文件 application.yml 中的配置值。 检查过该类已经交给 Spring 容器管理了,即已经在类上加了 Configuration 和 ConfigurationProperties(prefix &quo…...
CleanMyMac清理工具软件功能优势介绍
CleanMyMac更新最新版本x4.12,完美适配新版系统macOS10.14,拥有全新的界面。CleanMyMac可以让您安全、智能地扫描和清理整个系统,删除大型未使用的文件,减少iPod库的大小,最精确的应用程序卸载,卸载不必要的…...

【面试题】对JS中的事件冒泡、事件捕获、事件委托的理解
大厂面试题分享 面试题库后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库DOM事件流(event flow )存在三个阶段:事件捕获阶段、处于目标阶段、事件冒泡阶段。Dom标准事件流的触发的先…...

SAP 理解合并会计报表
随着企业集团的发展,集团内部会出现越来越多的公司;复杂的公司结构和复杂的集团内业务,使得集团内部管理困难重重,信息渠道严重失灵。除了内部管理的需要,企业还有义务向相关方提供详细的和及时的信息。ERP中的合并会计…...

Ubuntu 命令常用命令——定时启动程序
crontab -e 语法 crontab[ -u user ] file或 crontab[ -u user ] { -l | -r | -e }说明: crontab是用来让使用者在固定时间或固定间隔执行程序之用,换句话说,也就是类似使用者的时程表。 -U Lser 是指设定指定user的时程表,这个前提是你必…...
:走迷宫)
笔试题(十三):走迷宫
# 描述 # 定义一个二维数组 N*M ,如 5 5 数组下所示: # int maze[5][5] { # 0, 1, 0, 0, 0, # 0, 1, 1, 1, 0, # 0, 0, 0, 0, 0, # 0, 1, 1, 1, 0, # 0, 0, 0, 1, 0,}; # 它表示一个迷宫,其中的1表示墙壁,0表示可以走的路&#…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...
