Java 递归计算斐波那契数列指定位置上的数字
Java 递归计算斐波那契数列指定位置上的数字
- 一、原理
- 二、代码实现
- 三、运行结果
一、原理
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称“兔子数列”,其数值为:1、1、2、3、5、8、13、21、34……
在数学上,这一数列以如下递推的方法定义:F(0)=1,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)。
二、代码实现
要计算第 n 个斐波那契数列的数字,我们可以使用以下递归函数:
public class MyClass {public static void main(String[] args){int n = 10;System.out.println("斐波那契数列第 " + n + " 个数为 " + Fibonacci(n));}//递归 n代表第几个数public static int Fibonacci(int n) {//前两个数为 1//第三个数及后面的数为前面两数之和//如果输入的 n 不合法将返回 -1if (n == 1 || n == 2) {return 1;} else if (n > 2) {return Fibonacci(n - 1) + Fibonacci(n - 2);} else {return -1;}}}
时间复杂度:
- 最好情况下,当
n等于1或2时,直接返回1,时间复杂度为O(1)。 - 最坏情况下,当
n大于2时,需要递归调用Fibonacci()函数计算前两个数的和,时间复杂度为O(2^n)。因为每次递归调用会产生两个子问题,每个子问题又会产生两个更小的子问题,以此类推,直到递归到n等于1或2。 - 平均情况下,时间复杂度也是
O(2^n),因为每个数都需要通过递归调用计算得到。
空间复杂度:
- 由于递归调用会在堆栈中保存每次调用的局部变量和返回地址,所以空间复杂度取决于递归的深度。在最坏情况下,递归深度为
n,所以空间复杂度为O(n)。
综上所述,该递归实现的斐波那契数列函数的时间复杂度为指数级的 O(2^n),空间复杂度为线性的 O(n)。由于指数级的时间复杂度,在计算较大的斐波那契数时,递归实现会变得非常慢。
三、运行结果
斐波那契数列第 10 个数为 55
相关文章:

Java 递归计算斐波那契数列指定位置上的数字
Java 递归计算斐波那契数列指定位置上的数字 一、原理二、代码实现三、运行结果 一、原理 斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多斐波那契(Leonardo Fibonacci)以兔子繁殖为…...

ai数字人透明屏的应用场景有哪些?
AI数字人透明屏的应用场景: 银行、保险、售楼处等接待场景:AI数字人透明屏可以作为接待员,提供详细的信息和导航,提高客户体验和服务效率。 商业街、购物中心等场所:AI数字人透明屏可以作为导购员,提供商品…...

一、1、Hadoop的安装与环境配置
安装JDK: 首先检查Java是否已经安装: java -version 如果没有安装,点击链接https://www.oracle.com/technetwork/java/javase/downloads/jdk8-downloads-2133151.html 并选择相应系统以及位数下载(本文选择jdk-8u381-linux-x64…...
:论文实测YOLOv7模型涨点,超越现有多种G/D/C/EIoU,高效准确的边界框回归的损失)
剑指YOLOv7改进最新MPDIoU损失函数(23年7月首发论文):论文实测YOLOv7模型涨点,超越现有多种G/D/C/EIoU,高效准确的边界框回归的损失
💡本篇内容:剑指YOLOv7改进最新MPDIoU损失函数(23年7月首发论文):论文实测YOLOv7模型涨点,超越现有多种G/D/C/EIoU,高效准确的边界框回归的损失 💡🚀🚀🚀本博客 改进源代码改进 适用于 YOLOv7 按步骤操作运行改进后的代码即可 💡:重点:该专栏《剑指YOLOv7原…...
)
前端JavaScript面试100问(上)
1、解释一下什么是闭包 ? 闭包:就是能够读取外层函数内部变量的函数。闭包需要满足三个条件: 访问所在作用域;函数嵌套;在所在作用域外被调用 。 优点: 可以重复使用变量,并且不会造成变量污染 。缺点&am…...

C语言第九课------------------数组----------------C中之将
作者前言 作者介绍: 作者id:老秦包你会, 简单介绍: 喜欢学习C语言和python等编程语言,是一位爱分享的博主,有兴趣的小可爱可以来互讨 个人主页::小小页面 gitee页面:秦大大 一个爱分享的小博主 欢迎小可爱…...
MySQL的安装
掌握在Windows系统中安装MySQL数据库 MySQL的介绍 MySQL数据库管理系统由瑞典的DataKonsultAB公司研发,该公司被Sun公司收购,现在Sun公司又被Oracle公司收购,因此MySQL目前属于 Oracle 旗下产品。MySQL 软件采用了双授权政策,分…...
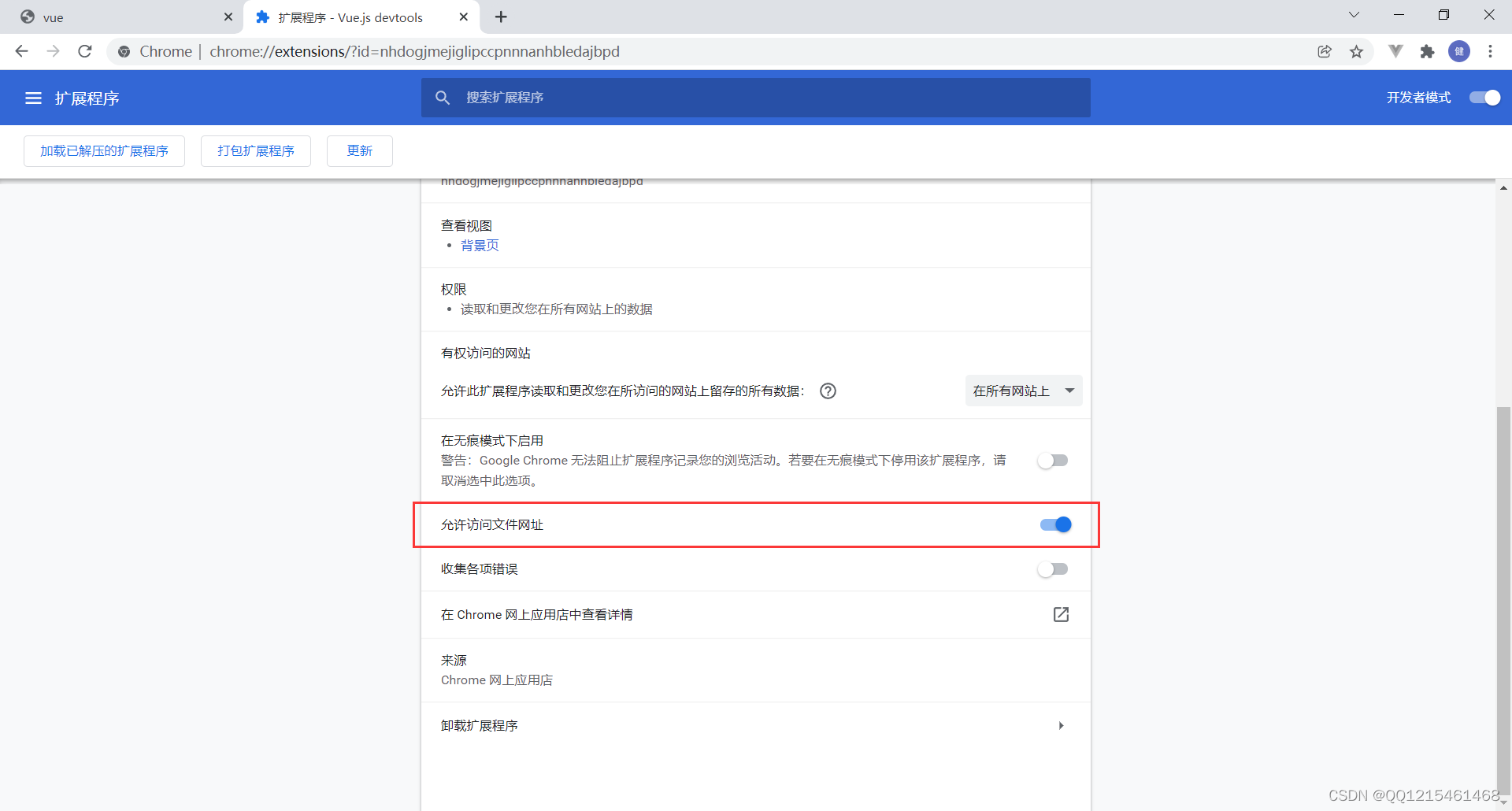
在Chrome(谷歌浏览器)中安装Vue.js devtools开发者工具及解决Vue.js not detected报错
文章目录 一、Vue.js devtools开发者工具安装1.打开谷歌浏览器——点击扩展程序——选择管理扩展程序2.先下载添加一个谷歌助手到扩展程序中(根据提示进行永久激活)3.点击谷歌浏览器的应用商店4.输入Vue.js devtools——搜索——选择下载 二、解决Vue.js…...
算法在MovieLens ml-100k数据集上构建精确的推荐系统:深入理解GroupLens数据的操作)
用Python实现概率矩阵分解(PMF)算法在MovieLens ml-100k数据集上构建精确的推荐系统:深入理解GroupLens数据的操作
第一部分:推荐系统的重要性以及概率矩阵分解的介绍 在如今的数字化时代,推荐系统在我们的日常生活中起着重要的作用。无论我们在哪个电商网站上购物,哪个音乐平台听歌,或者在哪个电影网站看电影,都会看到推荐系统的身影。它们根据我们的喜好和行为,向我们推荐可能喜欢的…...

WPF icon的设置
想给控件设置个圆形图片,代码如下: <Setter Property"Icon"><Setter.Value><Image Source"/WpfApp1;component/Resource/1.ico" Width"16" Height"16"/></Setter.Value></Setter&…...

使用frp中的xtcp映射穿透指定服务实现不依赖公网ip网速的内网穿透p2p
使用frp中的xtcp映射穿透指定服务实现不依赖公网ip网速的内网穿透p2p 管理员Ubuntu配置公网服务端frps配置service自启(可选) 配置内网服务端frpc配置service自启(可选) 使用者配置service自启(可选) 效果 通过frp实现内网client访问另外一个内网服务器 管理员 1)…...
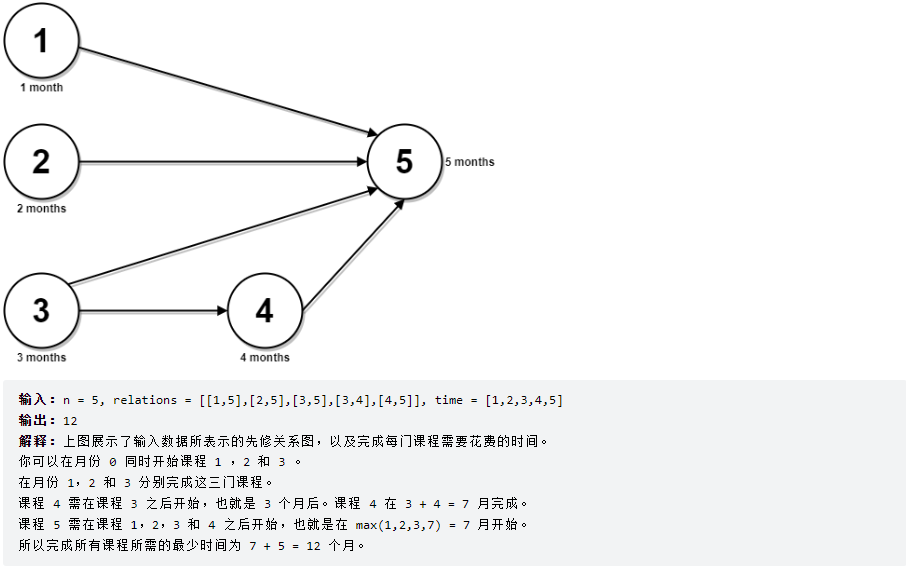
2023-07-28 LeetCode每日一题(并行课程 III)
2023-07-28每日一题 一、题目编号 2050. 并行课程 III二、题目链接 点击跳转到题目位置 三、题目描述 给你一个整数 n ,表示有 n 节课,课程编号从 1 到 n 。同时给你一个二维整数数组 relations ,其中 relations[j] [prevCoursej, next…...
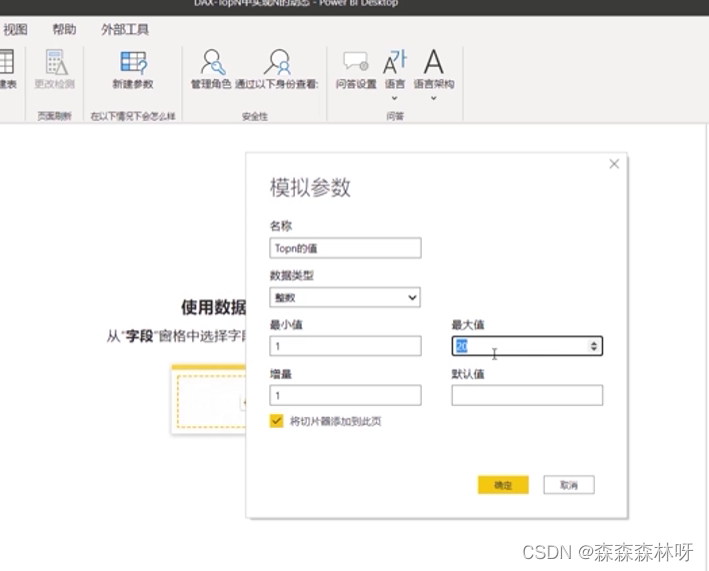
8.11 PowerBI系列之DAX函数专题-TopN中实现N的动态
需求 实现 1 ranking by amount rankx(allselected(order_2[产品名称]),[total amount]) 2 rowshowing_boolean var v_ranking [ranking by amount] var v_topN-no [topN参数 值] var v_result int( v_ranking < v_topN_no) return v_result 3 将度量值2放入视觉对象筛…...

后端性能测试的类型
目录 性能测试的类型 负载测试(load testing) 压力测试(Stress Testing) 可扩展性测试( 尖峰测试(Spike Testing) 耐久性测试(Endurance Testing) 并发测试(Concurrency Testing) 容量测试(Capacity Testing) 资料获取方法 性能测试的类型 性能测试:确定软…...

关闭Tomcat的日志输出
要关闭Tomcat的日志输出,您可以在Tomcat的配置文件中进行相应的调整。具体地说,您可以通过修改logging.properties文件来关闭Tomcat的日志输出。这个文件通常位于Tomcat的conf目录下。请按照以下步骤进行: 打开Tomcat安装目录,找…...

express 路由匹配和数据获取
express配置路由只需要通过app.method(url,func)来配置,其中url配置和其中的参数获取方法不同 直接写全路径 路由中允许存在. get请求传入的参数 router.get("/home", (req, res) > {res.status(200).send(req.query); });通过/home?a1会收到对象…...

62 | Python 操作 PDF
文章目录 Python 操作 PDF 教程1. 安装 PyPDF22. 读取 PDF 文件3. 创建 PDF 文件4. 修改 PDF 文件练习题1. 创建一个新的 PDF 文件,其中包含两个页面。第一个页面包含一段文本和一张图片,第二个页面包含一个表格。2. 打开练习题中创建的 PDF 文件,并将第一个页面中的文本修改…...

[SQL挖掘机] - 左连接: left join
介绍: 左连接是一种多表连接方式,它以左侧的表为基础,并返回满足连接条件的匹配行以及左侧表中的所有行,即使右侧的表中没有匹配的行。左连接将左表的每一行与右表进行比较,并根据连接条件返回结果集。 左连接的工作原理如下&am…...
Android 之 使用 SoundPool 播放音效
本节引言: 第九章给大家带来的是Android中的多媒体开发,与其说是多媒体开发还不如是多媒体相关API的 的使用,说下实际开发中我们做了一些和多媒体搭边的东西:拍照,录音,播放音乐,播放视频... 嗯…...

防火墙的ALG、NAT、双机热备知识点详解
具体的NAT和双机热备实验请到:NAT与双机热备实验 目录 1、ALG 2、NAT ALG 3、NAT域间双向转换 4、NAT域内双向转换 5、双出口NAT 6、防火墙的双机热备 解决方案1:VGMP 6.1 双机热备份技术产生的背景: 6.2 VRRP在多区域防火墙组网中的…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
