Acwing.91 最短Hamilton路径(动态规划)
题目
给定一张n个点的带权无向图,点从0~n-1标号,求起点0到终点n-1的最短Hamilton路径。Hamilton路径的定义是从0到n-1不重不漏地经过每个点恰好一次。
输入格式
第—行输入整数n。
接下来n行每行n个整数,其中第i行第j个整数表示点i到j的距离(记为a[i.i])。对于任意的, y,z,数据保证a[x,x]=0,a[x,y]=a[y,x]并且a[x,y]+aly,z]>=a[x,z]。
输出格式
输出一个整数,表示最短Hamilton路径的长度。
数据范围
1 ≤n ≤200≤a[i,j≤107
- 输入样例
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
- 输出样例:
18
题解
import java.util.Arrays;
import java.util.Scanner;/*** @author akuya* @create 2023-07-28-20:56*/
public class hamiltion {static int N=20;static int M=1<<N;static int n;static int w[][]=new int[N][N];static int f[][]=new int[M][N];public static void main(String[] args) {Scanner scanner=new Scanner(System.in);n=scanner.nextInt();for(int i=0;i<n;i++)for (int j = 0; j < n; j++)w[i][j]=scanner.nextInt();for(int i=0;i<M;i++){Arrays.fill(f[i],0x3f);}f[1][0]=0;for(int i=0;i<1<<n;i++)for(int j=0;j<n;j++)if((i>>j&1)!=0)for(int k=0;k<n;k++)if(((i-(1<<j))>>k&1)!=0)f[i][j]=Math.min(f[i][j],f[i-(1<<j)][k]+w[k][j]);System.out.println(f[(1<<n)-1][n-1]);}
}思路
本题同样是状态压缩类的动态规划,具体思路如下图

i代表走过的点,状态转移用到达j点的倒数第二个点,转移方程得出为
f[i][j]=Math.min(f[i][j],f[i-(1<<j)][k]+w[k][j]);
注意边界条件即可
相关文章:

Acwing.91 最短Hamilton路径(动态规划)
题目 给定一张n个点的带权无向图,点从0~n-1标号,求起点0到终点n-1的最短Hamilton路径。Hamilton路径的定义是从0到n-1不重不漏地经过每个点恰好一次。 输入格式 第—行输入整数n。 接下来n行每行n个整数,其中第i行第j个整数表示点i到j的距…...

[hfut] [important] v4l2 vedio使用总结/opevx/ffpeg/v4l2/opencv/cuda
(158条消息) linux驱动camera//test ok_感知算法工程师的博客-CSDN博客 (158条消息) linux V4L2子系统——v4l2架构(1)之整体架构_感知算法工程师的博客-CSDN博客 (158条消息) linux V4L2子系统——v4l2的结构体(2)之video_devi…...

2023年深圳杯数学建模A题影响城市居民身体健康的因素分析
2023年深圳杯数学建模 A题 影响城市居民身体健康的因素分析 原题再现: 以心脑血管疾病、糖尿病、恶性肿瘤以及慢性阻塞性肺病为代表的慢性非传染性疾病(以下简称慢性病)已经成为影响我国居民身体健康的重要问题。随着人们生活方式的改变&am…...

指令调度(Instruction Scheduling)
指令调度(Instruction Scheduling) 指令调度的约束基本机器模型基本块调度全局调度 指令调度是为了提高指令级并行(ILP),对于超长指令字(VLIW, Very Long Instruction Word)和多发射系统&#x…...

【运维】Linux 跨服务器复制文件文件夹
【运维】Linux 跨服务器复制文件文件夹 如果是云服务 建议用内网ip scp是secure copy的简写,用于在Linux下进行远程拷贝文件的命令,和它类似的命令有cp,不过cp只是在本机进行拷贝不能跨服务器,而且scp传输是加密的。可能会稍微影…...

k8s apiserver如何支持http访问?
原本是可以通过设置api-server的--insecure-port来实现,但是这个参数已经被废弃了,更好的方法则是使用proxy来实现: 在集群任意一个节点上起一个proxy服务,并设置允许所有host访问: kubectl proxy --address0.0.0.0 …...

Safetensors,高效安全易用的深度学习新工具
大家好,本文将介绍一种为深度学习应用提供速度、效率、跨平台兼容性、用户友好性和安全性的新工具。 Safetensors简介 Hugging Face开发了一种名为Safetensors的新序列化格式,旨在简化和精简大型复杂张量的存储和加载。张量是深度学习中使用的主要数据…...
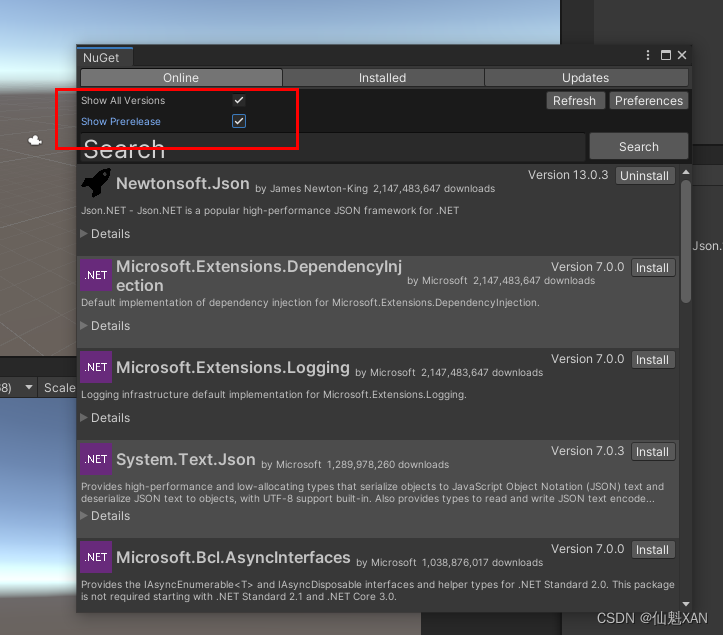
Unity 工具之 NuGetForUnity 包管理器,方便在 Unity 中的进行包管理的简单使用
Unity 工具之 NuGetForUnity 包管理器,方便在 Unity 中的进行包管理的简单使用 目录 Unity 工具之 NuGetForUnity 包管理器,方便在 Unity 中的进行包管理的简单使用 一、简单介绍 二、NuGetForUnity 的下载导入 Unity 三、NuGetForUnity 在 Unity 的…...
运算放大器(二):恒流源
一、实现原理 恒流源的输出电流能够在一定范围内保持稳定,不会随负载的变化而变化。 通过运放,将输入的电压信号转换成满足一定关系的电流信号,转换后的电流相当一个输出可调的简易恒流源。 二、电路结构 常用的恒流源电路如…...
企业选择租用CRM还是一次性买断CRM?分别有哪些优势?
CRM是企业管理客户关系,提升销售业绩,实现业务增长的重要工具。市场上的CRM系统销售方式主要有两种——租用型和买断型。那么,租用CRM好还是一次性买断CRM好?本文将从以下几个方面进行分析: 1、什么是租用型CRM和买断…...

VBA_MF系列技术资料1-133
MF系列VBA技术资料 为了让广大学员在实际VBA编程中有切实可行的思路及有效的提高自己的编程技巧,我参考大量的资料,并结合自己的经验总结了这份MF系列VBA技术综合资料,而且开放源码(MF04除外),其中MF01-04属…...

Android 项目架构
🔥 什么是架构 🔥 在维基百科里是这样定义的: 软件架构是一个系统的轮廓 . 软件架构描述的对象是直接构成系统的抽象组件. 各个组件之间的连接则明确和相对细致地描述组件之间的通讯 . 在实现阶段, 这些抽象组件被细化为实际组件 , 比如具体某个类或者对象 . 面试的过程中…...

【Linux】进程通信 — 管道
文章目录 📖 前言1. 通信背景1.1 进程通信的目的:1.2 管道的引入: 2. 匿名管道2.1 匿名管道的原理:2.2 匿名管道的创建:2.3 父子进程通信:2.3.1 read()阻塞等待 2.4 父进程给子进程派发任务:2.5…...
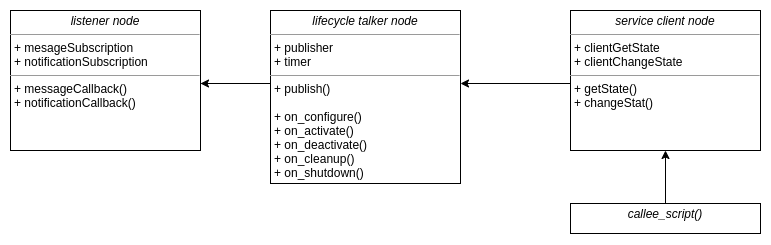
ROS 2 — 托管(生命周期)节点简介
一、说明 这篇文章是关于理解ROS 2中托管(生命周期)节点的概念。我们描述了概念性的想法以及我们为什么需要它。所以让我们开始吧! 二、托管式节点 — 什么和为什么? 为了理解托管式节点,让我们从一个简单的问题陈述开…...
)
vue2企业级项目(六)
vue2企业级项目(六) 自定义指令 创建src/directive/index.js const directives require.context("./modules", true, /\.js$/);export default {install: (Vue) > {directives.keys().forEach((key) > {let directive directives(key…...

OSPF的选路原则
域内 --- 1类,2类LSA 域间 --- 3类LSA 域外 --- 5类,7类LSA --- 根据开销值的计算规则不同,还分为类型1和类型2 1.如果学到的路由都是通过1类,2类LSA获取的域内路由 --- 这种情况直接比较开销值,优先选择开销值小的路…...

4.操作元素属性
4.1操作元素常用属性 ●通过 JS 设置/修改 标签元素属性,比如通过src更换图片 ●最常见的属性比如:href、 title、 src 等 ●语法: 对象.属性 值【示例】 // 1.获取元素 const pic document.querySelector( img ) // 2.操作元素 pic.src ./images/b…...
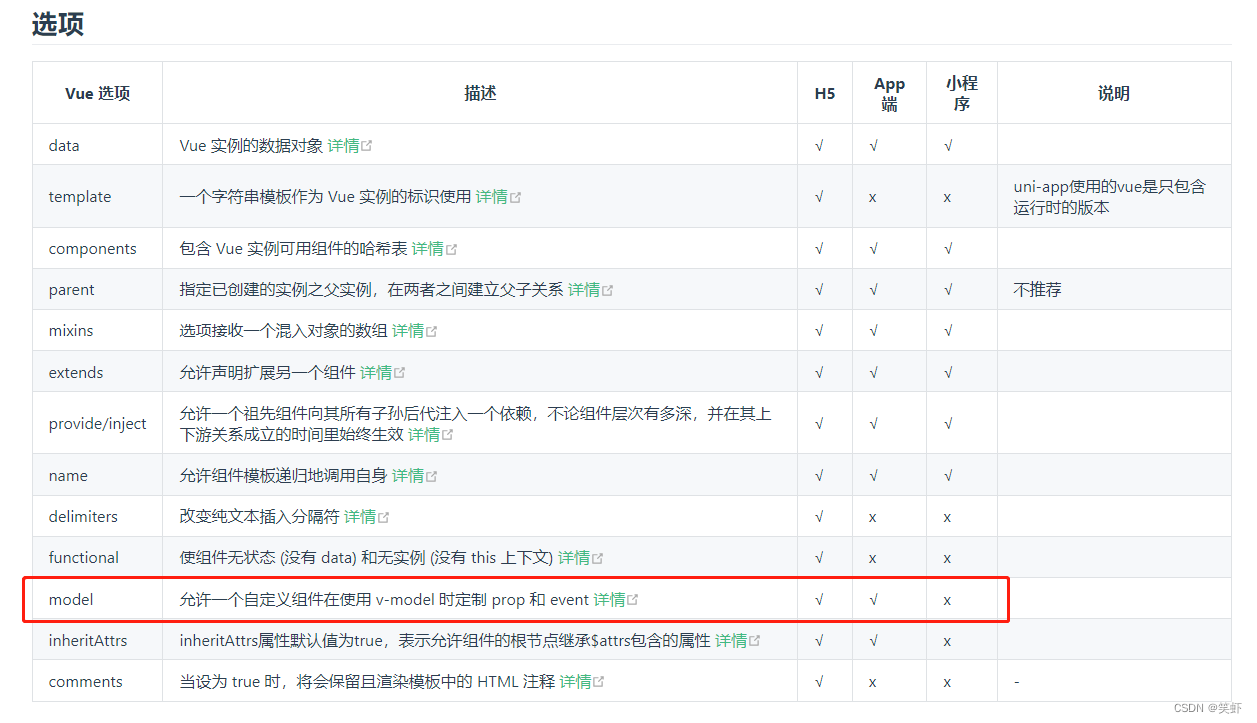
uniapp 微信小程序:v-model双向绑定问题(自定义 props 名无效)
uniapp 微信小程序:v-model双向绑定问题(自定义 props 名无效) 前言问题双向绑定示例使用 v-model使用 v-bind v-on使用 sync 修饰符 参考资料 前言 VUE中父子组件传递数据的基本套路: 父传子 props子传父 this.$emit(事件名, …...

【Lua学习笔记】Lua进阶——Table(3) 元表
接上文 文章目录 元表__tostring__call__index__newindex运算符元方法其它元表操作 元表 Q:为什么要使用元表? A:在Lua中,常常会需要表与表之间的操作。元表中提供了一些元方法,通过自定义元方法可以实现想要的功能&…...

AI编程常用工具 Jupyter Notebook
点击上方蓝色字体,选择“设为星标” 回复”云原生“获取基础架构实践 深度学习编程常用工具 我们先来看 4 个常用的编程工具:Sublime Text、Vim、Jupyter。虽然我介绍的是 Jupyter,但并不是要求你必须使用它,你也可以根据自己的喜…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
