【Vuvuzela 声音去噪算法】基于流行的频谱减法技术的声音去噪算法研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
Vuvuzela是一种喇叭形状的乐器,在足球比赛等场合中经常被使用。然而,Vuvuzela产生的噪声往往会对音频录音和通信应用造成干扰。基于流行的频谱减法技术的声音去噪算法可以用于去除Vuvuzela噪声。
频谱减法是一种常见的声音去噪技术,它基于噪声和信号在频域上的差异。该算法的主要思想是对输入信号进行频谱分析,并通过减去估计的噪声频谱来抑制噪声成分,从而实现去噪效果。
对于Vuvuzela声音去噪的研究,首先需要获取一段包含Vuvuzela噪声的录音样本。接下来,在时域上对录音样本进行分帧处理,每帧的长度通常是几十毫秒到几百毫秒。
然后,对每一帧的信号进行快速傅里叶变换 (FFT) 转换到频域。在频域上,可以将噪声和信号的频谱进行分离,并通过减去估计的噪声频谱来抑制Vuvuzela噪声成分。估计的噪声频谱通常通过平均多个帧或使用递归滤波器等方法得到。
最后,将去除噪声的频谱通过逆快速傅里叶变换 (IFFT) 转换回时域,得到去除Vuvuzela噪声的音频信号。
需要注意的是,频谱减法技术也存在一些局限性,例如可能会引入信号畸变、减少语音清晰度或对非噪声部分产生副作用。因此,在实际应用中,需要根据具体情况进行参数调整和优化,以平衡去噪效果和信号质量。此外,还可以结合其他声音处理方法,如时域滤波和混合滤波等,来进一步提高去噪效果。
📚2 运行结果

部分代码:
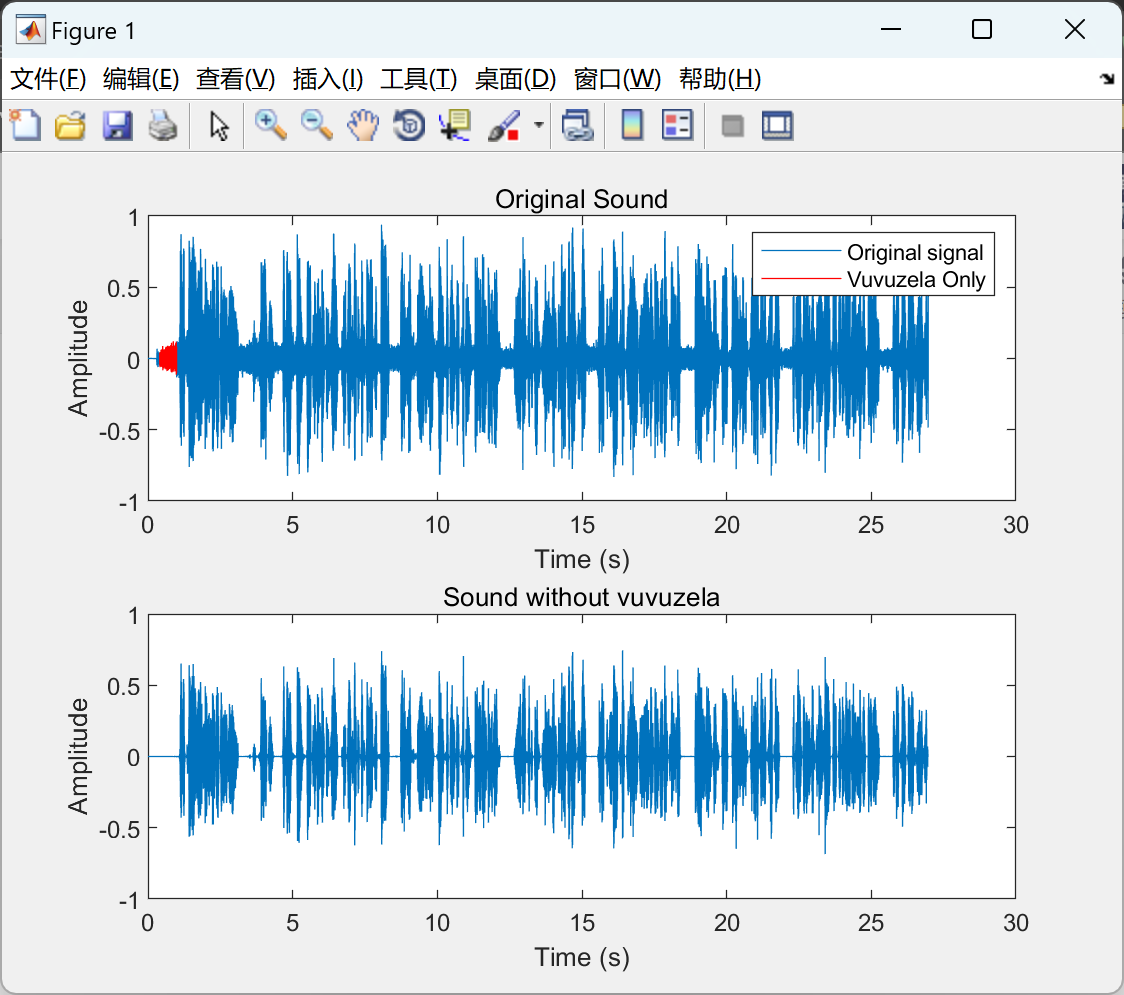
%show temporal signals
figure
subplot(2,1,1);
t_index=find(T>t_min & T<t_max);
plot([1:length(x)]/Fe,x);
xlabel('Time (s)');
ylabel('Amplitude');
hold on;
noise_interval=floor([T(t_index(1))*Fe:T(t_index(end))*Fe]);
plot(noise_interval/Fe,x(noise_interval),'r');
hold off;
legend('Original signal','Vuvuzela Only');
title('Original Sound');
%show denoised signal
subplot(2,1,2);
plot([1:length(output_signal)]/Fe,output_signal );
xlabel('Time (s)');
ylabel('Amplitude');
title('Sound without vuvuzela');
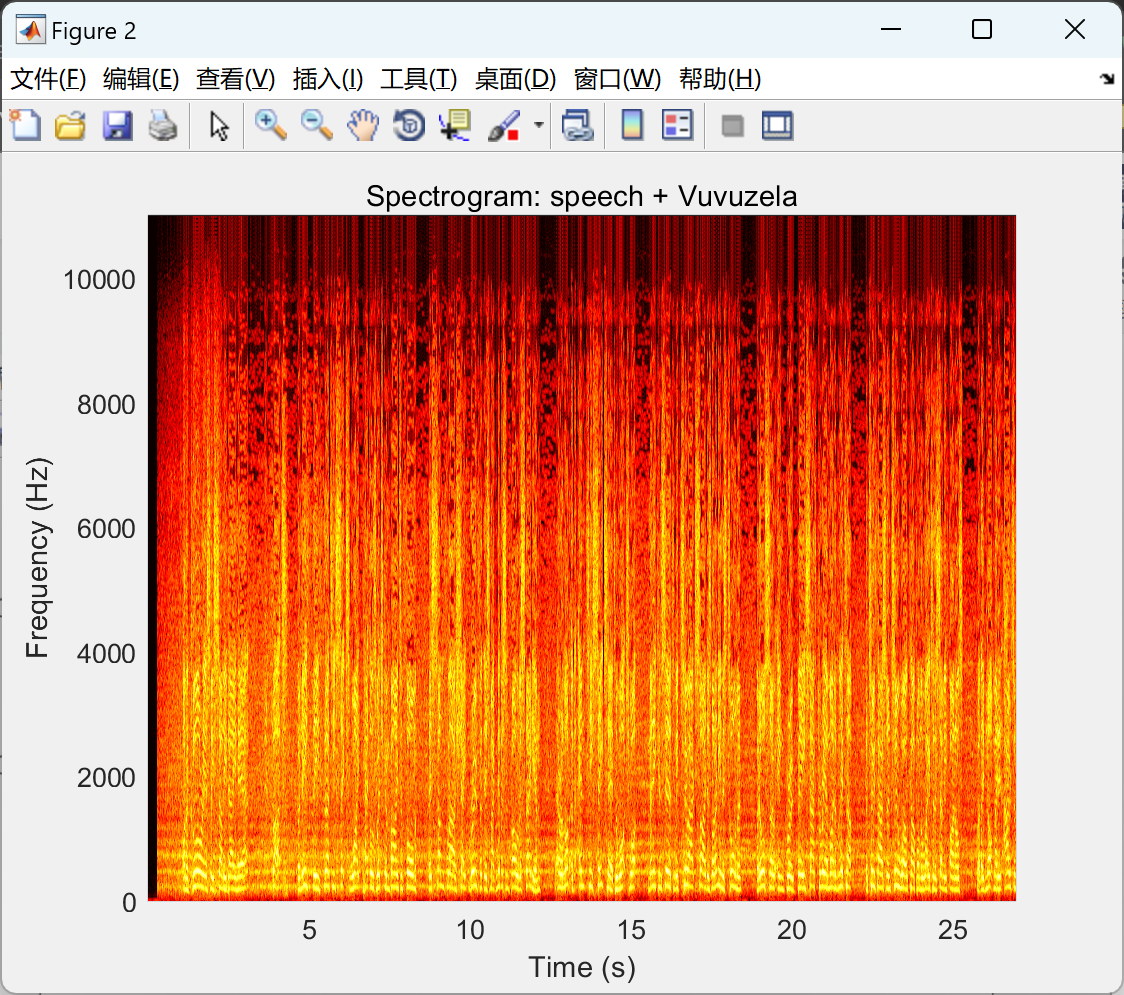
%show spectrogram
t_epsilon=0.001;
figure
S_one_sided=max(S(1:length(F)/2,:),t_epsilon); %keep only the positive frequency
pcolor(T,F(1:end/2),10*log10(abs(S_one_sided)));
shading interp;
colormap('hot');
title('Spectrogram: speech + Vuvuzela');
xlabel('Time (s)');
ylabel('Frequency (Hz)');
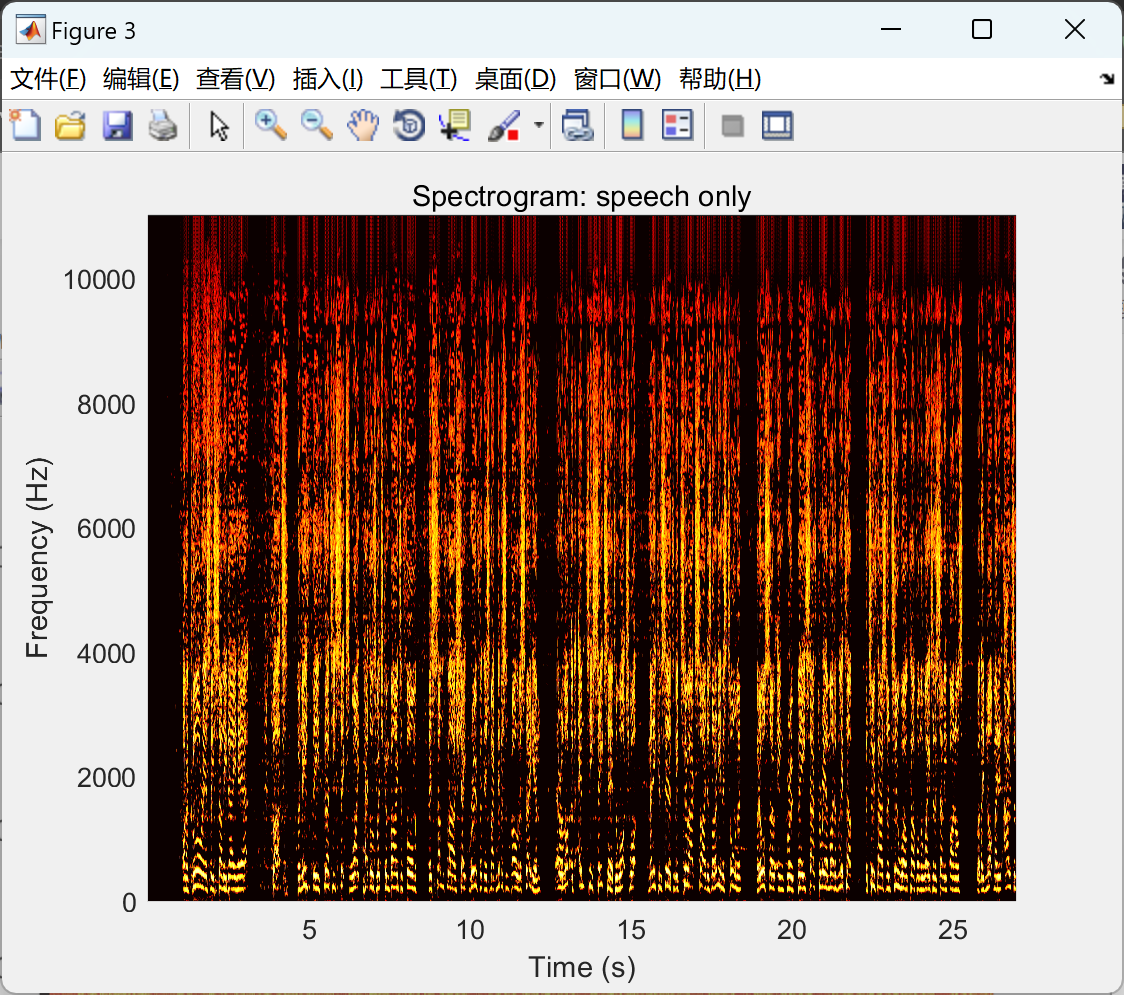
figure
S_one_sided=max(STFT(1:length(F)/2,:),t_epsilon); %keep only the positive frequency
pcolor(T,F(1:end/2),10*log10(abs(S_one_sided)));
shading interp;
colormap('hot');
title('Spectrogram: speech only');
xlabel('Time (s)');
ylabel('Frequency (Hz)');
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1] Steven F. Boll, "Suppression of Acoustic Noise in Speech Using Spectral Subtraction", IEEE Transactions on Signal Processing, 27(2),pp 113-120, 1979
[2] Y. Ephraim and D. Malah, “Speech enhancement using a minimum mean square error short-time spectral amplitude estimator,” IEEE. Transactions in Acoust., Speech, Signal Process., vol. 32, no. 6, pp. 1109–1121, Dec. 1984.
[3] S. Mallat, "A Wavelet Tour of Signal Processing", Academic Press, 3rd edition, 2008.
🌈4 Matlab代码实现
相关文章:

【Vuvuzela 声音去噪算法】基于流行的频谱减法技术的声音去噪算法研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
Vue + Element-ui组件上传图片报错问题解决方案
在前端开发中,我们经常需要模拟网络请求以进行单元测试或开发调试。而在模拟网络请求时,我们常常会使用到MockXMLHttpRequest对象。MockXMLHttpRequest对象是一个用于模拟XMLHttpRequest对象的工具,它提供了一种简单的方式来模拟网络请求&…...

java商城系统和php商城系统对比
java商城系统和php商城系统是两种常见的电子商务平台,它们都具有一定的优势和劣势。那么,java商城系统和php商城系统又有哪些差异呢? 一、开发难度 Java商城系统和PHP商城系统在开发难度方面存在一定的差异。Java商城系统需要使用Java语言进…...
某制造企业基于 KubeSphere 的云原生实践
背景介绍 随着业务升级改造与软件产品专案的增多,常规的物理机和虚拟机方式逐渐暴露出一些问题: 大量服务部署在虚拟机上,资源预估和硬件浪费较大;大量服务部署在虚拟机上,部署时间和难度较大,自动化程度…...
Electron 学习_BrowserWindow
BrowserWindow创建并控制浏览器窗口(主进程) 条件:在 app 模块 emitted ready 事件之前,您不能使用此模块。 1.在加载页面时,渲染进程第一次完成绘制时,如果窗口还没有被显示,渲染进程会发出 ready-to-show 事件 。 在…...
Docker学习笔记,包含docker安装、常用命令、dockerfile、docker-compose等等
😀😀😀创作不易,各位看官点赞收藏. 文章目录 Docker 学习笔记1、容器2、Docker 安装3、Docker 常用命令4、Docker 镜像5、自定义镜像5.1、镜像推送到阿里云5.2、镜像私有库 6、数据卷7、Docker 软件安装8、Docker File8.1、常见保…...
“ 错误的方法)
解决 “Module build failed (from ./node_modules/babel-loader/lib/index.js)“ 错误的方法
系列文章目录 文章目录 系列文章目录前言一、错误原因:二、解决方法:三、注意事项:总结 前言 在前端项目开发中,如果使用了 Babel 来转译 ES6 语法,有时会遇到错误信息 “Module build failed (from ./node_modules/b…...

go学习 6、方法
6、方法 面向对象编程(OOP),封装、组合。 6.1 方法声明 在函数声明时,在其名字之前放上一个变量,即是一个方法。这个附加的参数会将该函数附加到这种类型上,即相当于为这种类型定义了一个独占的方法。 …...
MySQL Windows版本下载及安装时默认路径的修改
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、MySQL 下载二、默认路径修改1、安装前准备【非常重要】2、启动安装程序总结1、MySQL下载2、MySQL默认路径修改前言 MySQL 被Oracle收购后,各种操作规范及约束也相应的跟着来了,这不,只…...
第3章 配置与服务
1 CoreCms.Net.Configuration.AppSettingsHelper using Microsoft.Extensions.Configuration; using Microsoft.Extensions.Configuration.Json; namespace CoreCms.Net.Configuration { /// <summary> /// 【应用设置助手--类】 /// <remarks> /// 摘要&#x…...
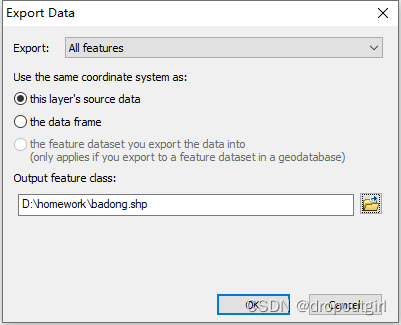
Arcgis之 KML/KMZ文件转shp
一般我们在Goole Earth上勾画的区域导出后都为KML或者KMZ格式的,但无法在arcgis等软件上直接应用,故需进行一定的转换 1.打开ArcMap,选择ArcToolbox->Conversion Tools->From KML->KML To Layer 得到如下结果(由于本KML…...

python绘制3D条形图
文章目录 数据导入三维条形图bar3d 数据导入 尽管在matplotlib支持在一个坐标系中绘制多组条形图,效果如下 其中,蓝色表示中国,橘色表示美国,绿色表示欧盟。从这个图就可以非常直观地看出,三者自2018到2022年的GDP变化…...

计算从曲线的起点到param指定的点的曲线段的长度
以下方法只能用于继承于AcDbCurve的类型 主要使用两个接口 派生类中此函数的实现应返回, 并将endParam设置为曲线端点的参数。 如果成功则返回Acad::eOk。 默认情况下, 该函数返回Acad::eNotImplemented。 virtual Acad::ErrorStatus getEndParam(double&endParam) cons…...

POLARDB IMCI 白皮书 云原生HTAP 数据库系统 一 数据压缩和打包处理与数据更新
开头还是介绍一下群,如果感兴趣polardb ,mongodb ,mysql ,postgresql ,redis 等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请联系 liuaustin3 ,在新加的朋友会分到2群(共…...
)
linux----源码安装如何加入到系统服务中(systemclt)
将自己源码安装的软件加入到系统服务中。例如nginx,mysql 就以nginx为例,源码安装,加入到系统服务中 使用yum安装nginx,自动会加入到系统服务 16-Linux系统服务 - 刘清政 - 博客园 (cnblogs.com) 第一步: 源码安装好nginx之后࿰…...
)
Unity 使用UnityWebRequest 读取存档 (IOS只能这样做)
打IOS包的时候发现的,不能使用正常的IO流读取,不然会读取不到数据,只能使用UnityWebRequest 读取 代码如下 public IEnumerator ReadArchive(Action<bool, string> ac, string filepath ""){UnityWebRequest request Unit…...

Caused by: org.springframework.beans.factory.
问题解决:Caused by: org.springframework.beans.factory.BeanCreationException: Error creating bean with name IUserRepository defined in app.test4.OpportunityMatching.IUserRepository defined in EnableJpaRepositories declared on JpaRepositoriesRegistrar.Enable…...

【docker 安装】 与【docker-compose 安装】
不同的操作系统需要不同的docker安装文件:具体下载位置: Docker: https://download.docker.com/linux/static/stable/ docekr-compose:https://github.com/docker/compose/releases 1. 验证客户机器是否有docker 和docker-compose docker -…...

意外:WPS编程新工具,不用编程,excel用户:可以不用VBA啦
来来来,拓宽一下视野! 别总以为excel和WPS只能用VBA编程,也别总是想着ACCESS这些老生常谈的工具。其实对于电子表格高级用户来讲,不会VBA,不用ACCESS,也一样可以解决复杂问题或者高级应用。 尤其是WPS用户…...

GAMES101 笔记 Lecture12 Geometry3
目录 Mesh Operations: Geometry ProcessingMesh Subdivision (曲面细分)Mesh Simplification(曲面简化)Mesh Regularization(曲面正则化) Subdivision(细分)Loop Subdivision(Loop细分)如何来调整顶点位置呢?Loop Subdivision Result (Loop细分的结果) Catmull-Cla…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

